爬楼梯问题-从暴力递归到动态规划(java)
爬楼梯,每次只能爬一阶或者两阶,计算有多少种爬楼的情况
- 爬楼梯--题目描述
- 暴力递归
- 递归+缓存
- 动态规划
- 暴力递归到动态规划专题
爬楼梯–题目描述
一个总共N 阶的楼梯(N > 0)
每次只能上一阶或者两阶。问总共有多少种爬楼方式。
示例1:
N = 1,
一步上去了,返回1.
示例2:
N = 2时。
可以第一次上一阶,再上一阶,这是一种方式,
也可以一次直接上两阶,这也是一种方式,
返回 2;
示例3:
N = 3:
可以选择, 1 1 1,
1 2
2 1
三种方式上楼,
返回3.
暴力递归
解题思路:
先确认base case:
只有一层台阶时 有1种方式,
只有两层台阶时 有两种方式,
当N 层台阶时,
当前这一步能选择上一层或者上两层两种可能性
因此f(N) = f(N - 1) + f(N - 2)
代码已经呼之欲出了:
代码演示:
/*** 暴力递归。* @param N* @return*/public static int paLouTi(int N){if (N <= 0){return 0;}return process(N);}/*** N层测楼梯 每次只能上一步或者两步,* 总共有多少种爬楼的方式。* @param N*/public static int process(int N){//base caseif (N == 1 || N == 2){return N;}return process(N - 1) + process(N - 2);}递归+缓存
解题思路:
第一先找到重复计算的地方。
第二步把重复计算的放进缓存里,记忆化搜索
这个里面的重复计算我们举个例子:
f(5) = f(4) + f(3)
f(4) = f(3) + f(2)
这里面f(3)就在重复计算,
我们把他加进缓存里
代码演示
/*** 递归加缓存的方式* @param N* @return*/public static int paLouTi2(int N){if (N <= 0){return 0;}int[] ans = new int[N + 1];return process2(N,ans);}/*** 带缓存的递归 记忆化搜索* @param N* @param ans* @return*/public static int process2(int N,int[]ans){//如果有值 直接返回 不在计算if(ans[N] != 0){return ans[N];}if(N == 1 || N == 2){ans[N] = N;}else{ans[N] = process2(N - 1,ans)+process2(N - 2,ans);}return ans[N];}动态规划
动态规划就是在递归加缓存的基础上,做的改进,我们提前把缓存表计算出来,然后直接从缓存表里取值。
代码演示:
/*** 动态规划* @param N* @return*/public static int paLouTi3(int N ){if (N < 1){return 0;}//缓存表int[] dp = new int[N + 1];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= N;i++ ){dp[i] = dp[i - 1] + dp[i - 2];}return dp[N];}暴力递归到动态规划专题
走到指定位置有多少种方式-从暴力递归到动态规划(java)
零钱兑换,凑零钱问题,从暴力递归到动态规划(java)
斐波那契数列-从暴力递归到动态规划
相关文章:
)
爬楼梯问题-从暴力递归到动态规划(java)
爬楼梯,每次只能爬一阶或者两阶,计算有多少种爬楼的情况 爬楼梯--题目描述暴力递归递归缓存动态规划暴力递归到动态规划专题 爬楼梯–题目描述 一个总共N 阶的楼梯(N > 0) 每次只能上一阶或者两阶。问总共有多少种爬楼方式。 示…...

浏览器如何验证SSL证书?
浏览器如何验证SSL证书?当前SSL证书应用越来越广泛,我们看见的HTTPS网站也越来越多。点击HTTPS链接签名的绿色小锁,我们可以看见SSL证书的详细信息。那么浏览器是如何验证SSL证书的呢? 浏览器如何验证SSL证书? 在浏览器的菜单中…...
】:: ll 指令 :: 查看指定目录下的文件详细信息)
Linux :: 【基础指令篇 :: 文件及目录操作:(10)】:: ll 指令 :: 查看指定目录下的文件详细信息
前言:本篇是 Linux 基本操作篇章的内容! 笔者使用的环境是基于腾讯云服务器:CentOS 7.6 64bit。 学习集: C 入门到入土!!!学习合集Linux 从命令到网络再到内核!学习合集 目录索引&am…...

Java字符集/编码集
1 字符集/编码集 基础知识 计算机中储存的信息都是用二进制数表示的;我们在屏幕上看到的英文、汉字等字符是二进制数转换之后的结果 按照某种规则, 将字符存储到计算机中,称为编码。反之,将存储在计算机中的二进制数按照某种规则解析显示出来,称为解码。这里强调一下: 按照…...
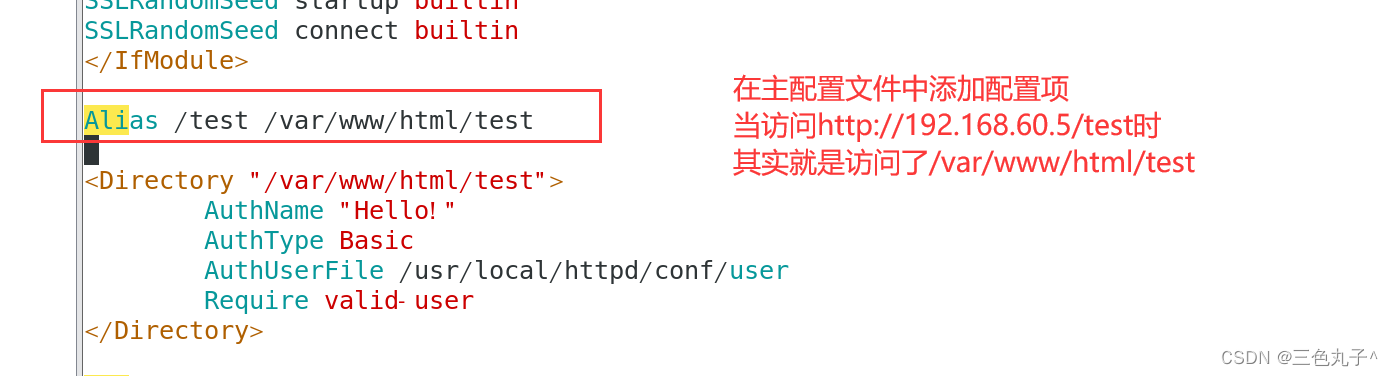
Apache配置与应用
目录 虚拟web主机httpd服务支持的虚拟主机类型基于域名配置方法基于IP配置方法基于端口配置方法 apache连接保持构建Web虚拟目录与用户授权限制Apache日志分割 虚拟web主机 虚拟Web主机指的是在同一台服务器中运行多个Web站点,其中每一个站点实际上并不独立占用整个…...
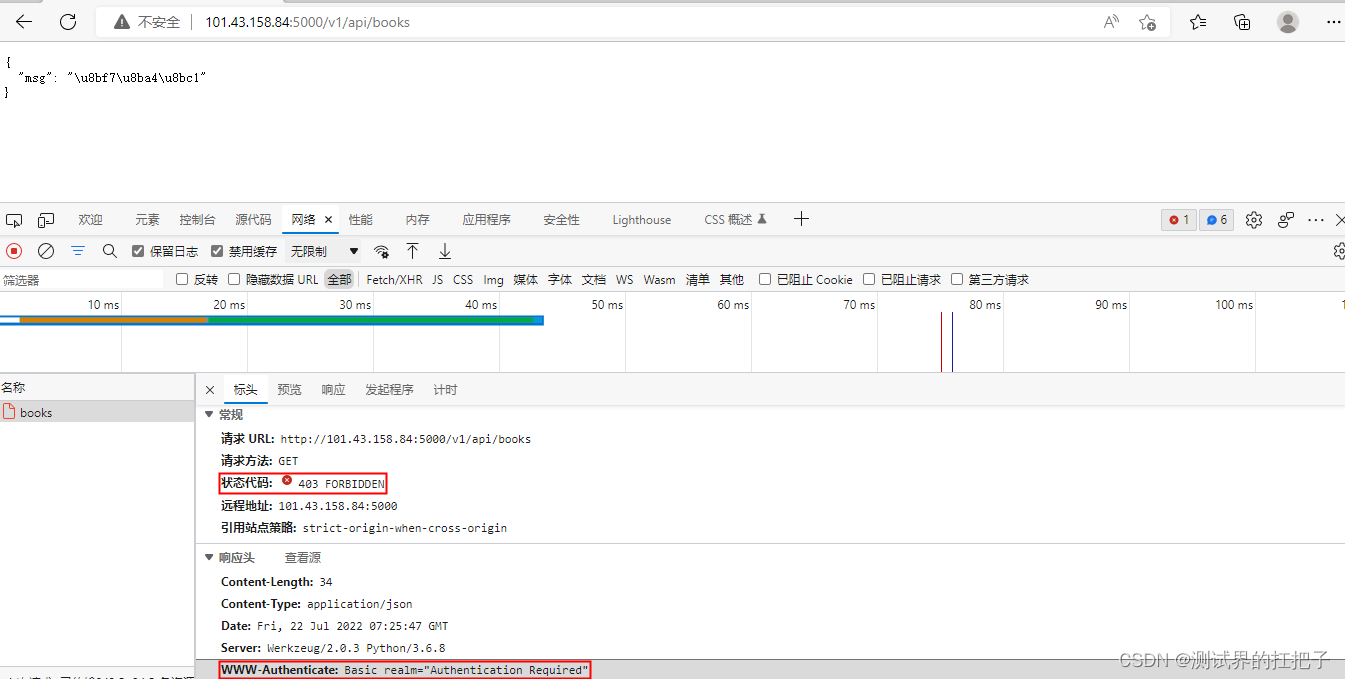
API自动化测试【postman生成报告】
PostMan生成测试报告有两种: 1、控制台的模式 2、HTML的测试报告 使用到一个工具newman Node.js是前端的一个组件,主要可以使用它来开发异步的程序。 一、控制台的模式 1、安装node.js 双击node.js进行安装,安装成功后在控制台输入node …...

探索OpenAI插件:ChatWithGit,memecreator,boolio
引言 在当今的技术世界中,插件扮演着至关重要的角色,它们提供了一种简单有效的方式来扩展和增强现有的软件功能。在本文中,我们将探索三个OpenAI的插件:ChatWithGit,memecreator,和boolio,它们…...

linux irq
中断上下部 软中断、tasklet、工作对列 软中断优点:运行在软中断上下文,优先级比普通进程高,调度速度快。 缺点:由于处于中断上下文,所以不能睡眠。 相对于软中断/tasklet,工作对列运行在进程上下文 h…...
使用详解)
串口流控(CTS/RTS)使用详解
1.流控概念 在两个设备正常通信时,由于处理速度不同,就存在这样一个问题,有的快,有的慢,在某些情况下,就可能导致丢失数据的情况。 如台式机与单片机之间的通讯,接收端数据缓冲区已满࿰…...

kube-proxy模式详解
1 kube-proxy概述 kubernetes里kube-proxy支持三种模式,在v1.8之前我们使用的是iptables 以及 userspace两种模式,在kubernetes 1.8之后引入了ipvs模式,并且在v1.11中正式使用,其中iptables和ipvs都是内核态也就是基于netfilter&…...
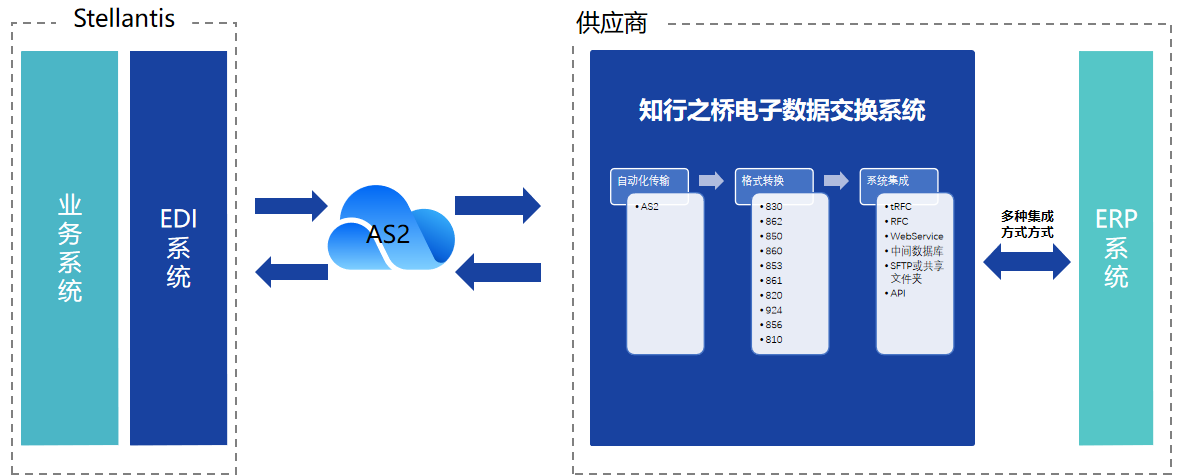
汽车EDI:如何与Stellantis建立EDI连接?
Stellantis 是一家实力雄厚的汽车制造公司,由法国标致雪铁龙集团(PSA集团)和意大利菲亚特克莱斯勒汽车集团(FCA集团)合并而成,是世界上第四大汽车制造商,拥有包括标致、雪铁龙、菲亚特、克莱斯勒…...

【SCI征稿】1区计算机科学类SCI, 自引率低,对国人友好~
一、【期刊简介】 JCR1区计算机科学类SCI&EI 【期刊概况】IF: 7.0-8.0,JCR1区,中科院2区; 【终审周期】走期刊系统,3-5个月左右录用; 【检索情况】SCI&EI双检; 【自引率】1.30% 【征稿领域】发表人工智能…...

Vue.js优化策略与性能调优指南
导语:Vue.js是一款出色的前端框架,但在处理大规模应用或复杂场景时,性能问题可能会出现。本文将介绍一些Vue.js优化策略和性能调优指南,帮助您提升应用的性能和用户体验。 延迟加载:将应用的代码进行按需加载ÿ…...
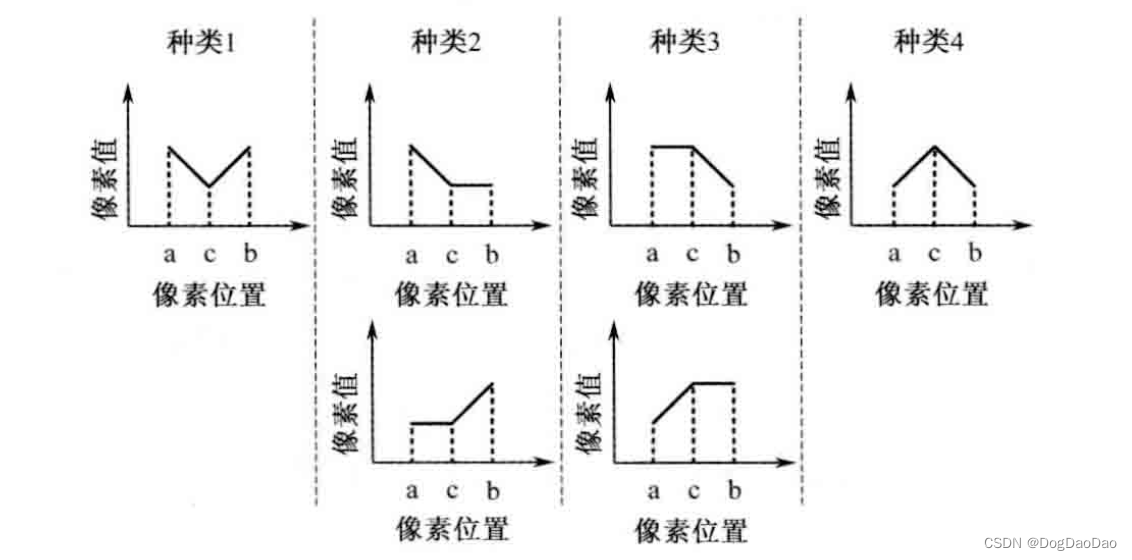
HEVC环路后处理核心介绍
介绍 为什么需要环路后处理技术 hevc采用基于快的混合编码框架,方块效应、振铃效应、颜色偏差、图像模糊等失真效应依旧存在,为了降低此类失真影响,需要进行环路滤波技术; 采用的技术 去方块滤波DF,为了降低块效应…...
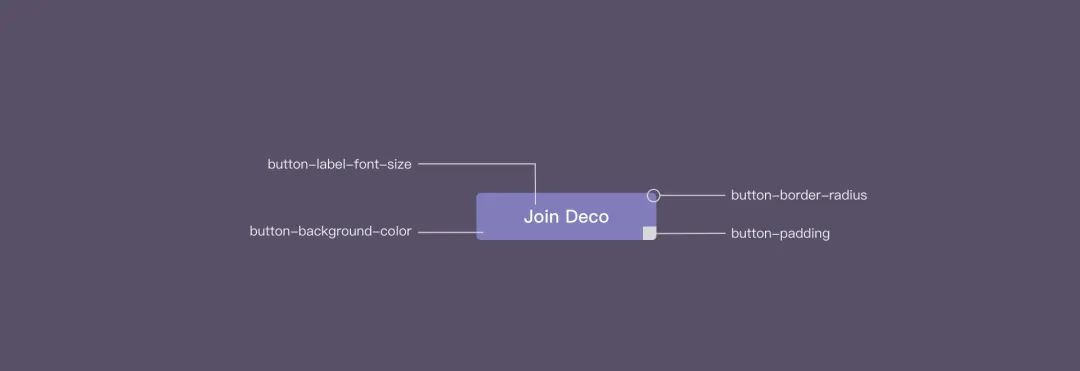
从组件化角度聊聊设计工程化
目录 设计系统 设计系统的定义 设计系统的优势 设计系统存在的问题 设计工程化 设计系统探索 设计系统落地实践 Design Token Design Token 实践 设计工程化理想方案构想 展望 参考文献 近几年围绕业务中台化的场景,涌现出了许多低代码平台。面对多组件…...

apache的配置和应用
文章目录 一、httpd服务支持的虚拟主机类型包括以下三种:二、构建Web虚拟目录与用户授权限制三、日志分割 虚拟Web主机指的是在同一台服务器中运行多个Web站点,其中每一个站点实际上并不独立占用整个服务器,因此被称为“虚拟”Web 主机。通过虚拟 Web 主…...
Buf 教程 - 使用 Protobuf 生成 Golang 代码和 Typescript 类型定义
简介 Buf 是一款更高效、开发者友好的 Protobuf API 管理工具,不仅支持代码生成,还支持插件和 Protobuf 格式化。 我们可以使用 Buf 替代原本基于 Protoc 的代码生成流程,一方面可以统一管理团队 Protoc 插件的版本、代码生成配置ÿ…...
)
Java 锁 面试题(ReentrantLock、synchronized)
Java 锁 面试题(ReentrantLock、synchronized) 1. 锁2. ReentrantLock2.1 ReentrantLock 的实现原理2.2 AQS 是什么?2.3 CAS 是什么? 3. synchronized3.1 synchronized 的实现原理3.2 synchronized 的锁升级过程3.2.1 无锁3.2.2 偏…...

Python中的缩进是什么意思?
在Python中,缩进是指在代码中使用空格或制表符来表示代码块的层次结构。Python使用缩进作为语法的一部分,以定义代码的逻辑结构和代码块的范围。缩进在Python中具有以下几个重要的方面和含义。 代码块的开始和结束: 缩进在Python中用于标识代…...

2023年9月数学建模:最小二乘优化、曲线拟合与函数逼近
2023年9月数学建模国赛期间提供ABCDE题思路加Matlab代码,专栏链接(赛前一个月恢复源码199,欢迎大家订阅):http://t.csdn.cn/Um9Zd 目录 1. 最小二乘优化 1.1 最小二乘优化的原理 1.2 最小二乘优化的方法...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
