代码随想录算法训练营第五十二天|300.最长递增子序列|674. 最长连续递增序列|718. 最长重复子数组
LeetCode300.最长递增子序列
动态规划五部曲:
1,dp[i]的定义:本题中,正确定义dp数组的含义十分重要。dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为在做递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算递增呢。
2,状态转移方程:位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
3,dp[i]的初始化:每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1。
4,确定遍历顺序:dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历。j其实就是遍历0到i-1,那么是从前到后,还是从后到前遍历都无所谓,只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历。
5,举例推导dp数组:输入:[0,1,0,3,2],dp数组的变化如下:
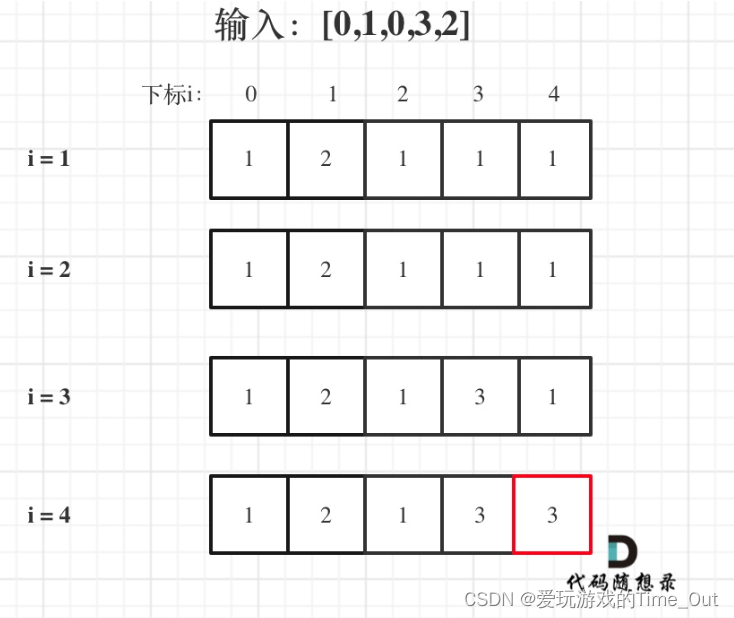
Java代码如下:
public int lengthOfLIS(int[] nums) {int[] dp = new int[nums.length];Arrays.fill(dp, 1);for (int i = 0; i < dp.length; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}}int res = 0;for (int i = 0; i < dp.length; i++) {res = Math.max(res, dp[i]);}return res;}
LeetCode674. 最长连续递增序列
动态规划五部曲:
1,确定dp数组(dp table)以及下标的含义:dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]。注意这里的定义,一定是以下标i为结尾,并不是说一定以下标0为起始位置。
2,确定递推公式:如果 nums[i] > nums[i - 1],那么以 i 为结尾的连续递增的子序列长度 一定等于 以i - 1为结尾的连续递增的子序列长度 + 1 。即:dp[i] = dp[i - 1] + 1;因为本题要求连续递增子序列,所以就只要比较nums[i]与nums[i - 1],而不用去比较nums[j]与nums[i] (j是在0到i之间历)。既然不用j了,那么也不用两层for循环,本题一层for循环就行,比较nums[i] 和 nums[i - 1]。
3,dp数组如何初始化:以下标i为结尾的连续递增的子序列长度最少也应该是1,即就是nums[i]这一个元素。所以dp[i]应该初始1;
4,确定遍历顺序:从递推公式上可以看出, dp[i + 1]依赖dp[i],所以一定是从前向后遍历。
5,举例推导dp数组:已输入nums = [1,3,5,4,7]为例,dp数组状态如下:
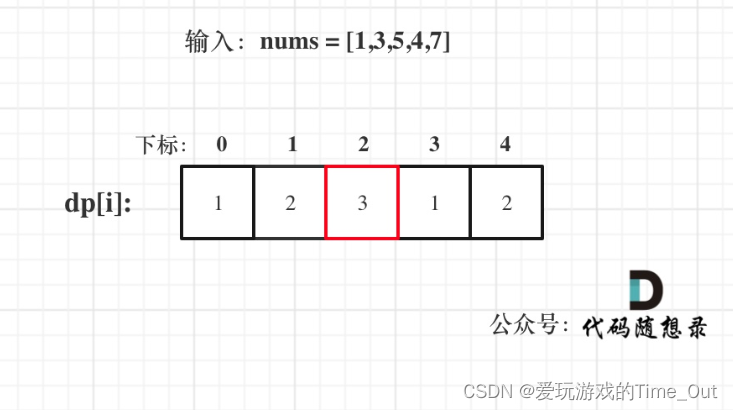
Java代码如下:
public int findLengthOfLCIS(int[] nums) {int[] dp = new int[nums.length];for (int i = 0; i < dp.length; i++) {dp[i] = 1;}int res = 1;for (int i = 0; i < nums.length - 1; i++) {if (nums[i + 1] > nums[i]) {dp[i + 1] = dp[i] + 1;}res = res > dp[i + 1] ? res : dp[i + 1];}return res;} 
LeetCode718. 最长重复子数组
动态规划五部曲:
1,确定dp数组(dp table)以及下标的含义:dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )。那dp[0][0]是什么含义呢?总不能是以下标-1为结尾的A数组吧。其实dp[i][j]的定义也就决定着,我们在遍历dp[i][j]的时候i 和 j都要从1开始。
2,确定递推公式:根据dp[i][j]的定义,dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。即当A[i - 1] 和B[j - 1]相等的时候,dp[i][j] = dp[i - 1][j - 1] + 1;根据递推公式可以看出,遍历i 和 j 要从1开始!
3,dp数组如何初始化:根据dp[i][j]的定义,dp[i][0] 和dp[0][j]其实都是没有意义的!但dp[i][0] 和dp[0][j]要初始值,因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;所以dp[i][0] 和dp[0][j]初始化为0。举个例子A[0]如果和B[0]相同的话,dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,正好符合递推公式逐步累加起来。
4,确定遍历顺序:外层for循环遍历A,内层for循环遍历B。那又有同学问了,外层for循环遍历B,内层for循环遍历A。不行么?也行,一样的,我这里就用外层for循环遍历A,内层for循环遍历B了。同时题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来。
5,举例推导dp数组:拿示例1中,A: [1,2,3,2,1],B: [3,2,1,4,7]为例,画一个dp数组的状态变化,如下:

Java代码如下:
public int findLength(int[] nums1, int[] nums2) {int result = 0;int[][] dp = new int[nums1.length + 1][nums2.length + 1];for (int i = 1; i < nums1.length + 1; i++) {for (int j = 1; j < nums2.length + 1; j++) {if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;result = Math.max(result, dp[i][j]);}}}return result;}
相关文章:

代码随想录算法训练营第五十二天|300.最长递增子序列|674. 最长连续递增序列|718. 最长重复子数组
LeetCode300.最长递增子序列 动态规划五部曲: 1,dp[i]的定义:本题中,正确定义dp数组的含义十分重要。dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。为什么一定表示 “以nums[i]结尾的最长递增子序” ,…...

完全卸载mysql教程
引言 很多人因为第一次安装mysql导致安装错误,或者安装的数据库版本太高,比如mysql8.0版本,出现了很多问题,导致数据库无法使用,或者一些图形界面无法操作,想要卸载,重装稳定的mysql数据库&…...

4G开发板-安卓手机开发套件-MTK主板开发板定制
开发板是一种用于嵌入式系统开发的电路板,它包含了各种硬件组件,如中央处理器、存储器、输入设备、输出设备、数据通路/总线以及外部资源接口等。为了满足特定的开发需求,嵌入式系统开发者通常会根据项目要求来定制开发板,当然用户…...

人工智能十大新星揭晓,华人学者占90%
人工智能领域著名杂志 IEEE Intelligent Systems发布了 2022 年度“人工智能十大新星”(AIs 10 to Watch)名单 ,其中有九位都是华人研究者。知识人网小编推荐给大家。 近日,人工智能领域著名杂志 IEEE Intelligent Systems公布了 …...

ROS学习——通信机制(话题通信①—发布方实现)
2.1 话题通信 Autolabor-ROS机器人入门课程《ROS理论与实践》零基础教程 040话题通信(C)1_发布方框架_Chapter2-ROS通信机制_哔哩哔哩_bilibili 一、ROS 中的基本通信机制主要有如下三种实现策略 话题通信(发布订阅模式服务通信(请求响应模式)参数服务器(参数共享模式) 二、…...

【运筹优化】最短路算法之SPFA算法 + Java代码实现
文章目录 一、SPFA算法简介二、SPFA算法思想三、Java代码实现四、测试 一、SPFA算法简介 SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同…...
linuxOPS基础_linux权限管理
权限概述 什么是权限 在多用户计算机系统的管理中,权限是指某个特定的用户具有特定的系统资源使用权利。 在Linux 中分别有读、写、执行权限 \权限针对文件权限针对目录读r(read)表示可以查看文件内容;cat、less…表示可以(ls)查看目录中存在的文…...
linux安装homeassistant(智能设备远程控制开源框架)
1、安装docker 先切换到root 用户,先安装一些基本环境: yum install -y yum-utils device-mapper-persistent-data lvm2添加阿里云软件源 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo然后安装 D…...

TensorRT Triton Inference Server: 版本 error魔术标记不匹配 , NGC使用
魔术标记不匹配错误Serialization assertion magicTagRead kMAGIC_TAG failed.Magic tag does not match 原因: 转换和推理使用的镜像的标签是相同的,但是转换的镜像中pip list得到trt版本为8.6.0,但是推理环境中 rootf2c810ba3976:/# /usr/…...
)
Elasticsearch 文本分析器(下)
字符过滤器 注意:字符过滤器用于在将字符流传递给分词器之前对其进行预处理 html_strip HTML元素替换过滤器 此过滤器会替换掉HTML标签,且会转换HTML实体 如:& 会被替换为 &。 {"tokenizer": "keyword","…...

Git操作方法
目录 Git是什么 Git特点 Git作用 Git原理 集中式 分布式 Git安装 修改语言 Git操作 1.初始化Git仓库 2.提交工作区的内容到版本库 3.查看版本记录 4.版本回退 5.版本前进 Git 命令 通用操作 工作状态 版本回退 版本前进 远程仓 1.GitHub 2.GitLab 3.码云…...

CorelDRAW矢量绘图2023中文版下载
市面上的矢量绘图工具虽然很多,但权威又专业的却不多,选到不好用的工具,会极大的影响自己创作,CorelDRAW简称cdr,是一款功能强大的矢量图制作软件,一说到矢量图制作,大家都会不由自主地想到cdr。…...

Java-API简析_java.lang.Float类(基于 Latest JDK)(浅析源码)
【版权声明】未经博主同意,谢绝转载!(请尊重原创,博主保留追究权) https://blog.csdn.net/m0_69908381/article/details/131129886 出自【进步*于辰的博客】 其实我的【Java-API】专栏内的博文对大家来说意义是不大的。…...
pycharm的基本使用
废话文学 本人记录笔记始终遵循“能动手绝不动脑,能动脑绝不动手”的基本原则。不会的操作,跟着笔记干就完事了,还动啥脑袋?留着脑细胞刷抖音擦边小姐姐他不香吗? 什么是IDE IDE即【集成开发环境】,Inte…...
为什么要使用微软的 Application Framework?
我是荔园微风,作为一名在IT界整整25年的老兵,今天来看一下我们为什么要使用微软的 Application Framework? 虽然Application Framework 并不是新观念,它们却在最近数年才成为 PC 平台上软件开发的主流工具。面向对象语言是具体实…...

Python爬虫基础知识点
Python爬虫是使用Python编写的程序,可以自动抓取互联网上的数据。常用的Python爬虫框架包括Scrapy、BeautifulSoup、Requests等。Python爬虫可以应用于众多场合,如大数据分析、信息监测、数据挖掘和机器学习等领域。那么新手应该如何学习python爬虫呢&am…...

K8s运维备忘
1.服务器集群搭建: VagrantFile中加入以下代码,创建3个虚拟机: Vagrant.configure("2") do |config| (1..3).each do |i| config.vm.define "k8s-node#{i}" do |node| # 设置虚拟机的Box …...
)
激光雷达+rtk+rgb联合使用(4)
因为一直在忙一些乱七八糟的事情,就没顾得上继续写,想着快速收尾算了。 前面写到,我在点云的匹配上花了大量的时间,不断的调参数,换方法,一共几百个点云,想着先每50个匹配一次,得到几…...

【K8S系列】快速初始化⼀个最⼩集群
序言 走得最慢的人,只要不丧失目标,也比漫无目的地徘徊的人走得快。 文章标记颜色说明: 黄色:重要标题红色:用来标记结论绿色:用来标记一级重要蓝色:用来标记二级重要 希望这篇文章能让你不仅有…...
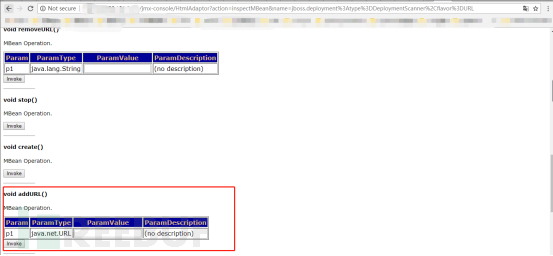
Exploit/CVE-2010-0738
打开JBoss的潘多拉魔盒:JBoss高危漏洞分析 *本文中涉及到的相关漏洞已报送厂商并得到修复,本文仅限技术研究与讨论,严禁用于非法用途,否则产生的一切后果自行承担。 前言 JBoss是一个基于J2EE的开放源代码应用服务器࿰…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
