最优化理论-KKT定理的推导与实现
目录
一、引言
二、最优化问题的基本概念
三、KKT条件的引入
1. 梯度条件
2. 原始可行性条件
3. 对偶可行性条件
四、KKT定理的表述
五、KKT定理的证明
1. 构造拉格朗日函数
2. 构造拉格朗日对偶函数
3. 推导KKT条件
4. 解释KKT条件
六、KKT定理的应用
七、总结
一、引言
最优化问题是数学中的一个重要分支,它研究如何在一定的限制条件下,寻找使某个目标函数取得最大或最小值的变量取值。最优化问题在实际应用中有着广泛的应用,例如在经济学、工程学、管理学等领域中都有着重要的应用。最优化问题的研究不仅可以帮助我们更好地理解现实世界中的问题,还可以为我们提供有效的解决方案。
在最优化问题中,KKT定理是一个非常重要的理论工具。KKT定理是最优化问题中的一个必要条件,它可以帮助我们判断一个解是否为最优解,并且可以为我们提供求解最优解的方法。本文将介绍最优化理论中的KKT定理,包括其定义、表述、证明和应用。
二、最优化问题的基本概念
在介绍KKT定理之前,我们需要先了解最优化问题的基本概念。最优化问题通常可以表示为以下形式:
其中,是一个
维向量,
是一个实值函数,称为目标函数;
和
是一些实值函数,称为约束条件。我们称上述问题为一个约束优化问题。
在约束优化问题中,我们需要找到一个满足所有约束条件的,使得
取得最小值。这个
就是我们所要求解的最优解。但是,在实际问题中,我们往往很难直接求解出最优解,因此需要借助一些数学工具来帮助我们求解。
三、KKT条件的引入
在介绍KKT定理之前,我们需要先引入KKT条件。KKT条件是一组必要条件,它可以帮助我们判断一个解是否为最优解。KKT条件包括以下三个部分:
1. 梯度条件
其中,是最优解,
和
是拉格朗日乘子。
2. 原始可行性条件
3. 对偶可行性条件
KKT条件是最优化问题中的一个必要条件,它可以帮助我们判断一个解是否为最优解。但是,KKT条件并不是充分条件,即满足KKT条件的解不一定是最优解。因此,我们需要引入KKT定理来判断一个解是否为最优解。
四、KKT定理的表述
KKT定理是最优化问题中的一个重要理论工具,它可以帮助我们判断一个解是否为最优解,并且可以为我们提供求解最优解的方法。KKT定理的表述如下:
设是一个约束优化问题的局部最优解,且满足原始可行性条件和对偶可行性条件,则存在一组拉格朗日乘子
和
,使得梯度条件成立。
KKT定理告诉我们,如果一个解满足原始可行性条件和对偶可行性条件,那么它一定满足梯度条件。因此,我们可以通过检验梯度条件来判断一个解是否为最优解。
五、KKT定理的证明
KKT定理的证明需要用到拉格朗日对偶性,具体证明过程可以分为以下几步:
1. 构造拉格朗日函数
首先,我们需要构造一个拉格朗日函数,它包含了原问题的约束条件和目标函数。具体地,对于原问题:
我们可以构造如下的拉格朗日函数:
其中, 和
是拉格朗日乘子,它们的取值可以通过对拉格朗日函数求导并令其为零来确定。
2. 构造拉格朗日对偶函数
接下来,我们需要构造拉格朗日对偶函数。具体地,我们将拉格朗日函数对 求最小值,得到:
注意到, 是一个凸函数,因此
也是一个凸函数。
3. 推导KKT条件
根据拉格朗日对偶性,我们有:
因此,我们可以得到以下的KKT条件:
其中,、
和
是拉格朗日函数的最优解。
4. 解释KKT条件
KKT条件告诉我们,如果一个点 是原问题的最优解,那么存在拉格朗日乘子
和
,满足上述条件。这些条件告诉我们,最优解
必须满足原问题的约束条件,同时,拉格朗日乘子
和
可以帮助我们判断约束条件是否被严格满足。
六、KKT定理的应用
KKT定理可以应用于各种最优化问题,包括线性规划、二次规划、非线性规划等。具体地,我们可以使用KKT条件来判断一个点是否是最优解,或者使用KKT条件来求解最优解。
下面是使用MATLAB实现KKT算法的步骤:
1. 定义优化问题的目标函数和约束条件。
2. 使用MATLAB的优化工具箱中的函数创建一个优化问题对象。
3. 使用KKT条件来求解优化问题。KKT条件是一组必要条件,用于判断一个点是否是最优解。在MATLAB中,可以使用fmincon函数来求解带有约束条件的优化问题,并使用输出参数来检查KKT条件是否满足。
下面是一个简单的例子,演示如何使用MATLAB实现KKT算法:
% 定义目标函数和约束条件
fun = @(x) x(1)^2 + x(2)^2; % 目标函数
nonlcon = @(x) [x(1) + x(2) - 1, x(1) - x(2) - 1]; % 约束条件% 创建优化问题对象
problem = struct();
problem.objective = fun;
problem.x0 = [0, 0];
problem.nonlcon = nonlcon;% 使用fmincon函数求解优化问题
[x, fval, exitflag, output, lambda] = fmincon(problem);% 检查KKT条件是否满足
grad = [2*x(1), 2*x(2)]; % 目标函数的梯度
c = nonlcon(x); % 约束条件的值
ceq = c(1); % 等式约束条件的值
cineq = c(2); % 不等式约束条件的值
lambda_eq = lambda.eqlin; % 等式约束条件的拉格朗日乘子
lambda_ineq = lambda.ineqlin; % 不等式约束条件的拉格朗日乘子
kkt1 = grad + lambda_eq*nonlcon(x)'; % KKT条件1
kkt2 = lambda_ineq; % KKT条件2
kkt3 = cineq; % KKT条件3if norm(kkt1) < 1e-6 && norm(kkt2) < 1e-6 && norm(kkt3) < 1e-6disp('KKT条件满足');
elsedisp('KKT条件不满足');
end在上面的例子中,我们定义了一个目标函数和两个约束条件。然后,我们使用MATLAB的优化工具箱中的函数创建一个优化问题对象,并使用fmincon函数求解该问题。最后,我们检查KKT条件是否满足。如果KKT条件满足,则说明我们找到了最优解。
七、总结
KKT定理是最优化理论中的重要定理,它告诉我们如何判断一个点是否是最优解,以及如何求解最优解。KKT定理的证明需要用到拉格朗日对偶性,具体证明过程可以分为构造拉格朗日函数、构造拉格朗日对偶函数、推导KKT条件和解释KKT条件四个步骤。
相关文章:
最优化理论-KKT定理的推导与实现
目录 一、引言 二、最优化问题的基本概念 三、KKT条件的引入 1. 梯度条件 2. 原始可行性条件 3. 对偶可行性条件 四、KKT定理的表述 五、KKT定理的证明 1. 构造拉格朗日函数 2. 构造拉格朗日对偶函数 3. 推导KKT条件 4. 解释KKT条件 六、KKT定理的应用 七、总结 …...

chatgpt赋能python:Python中引入其他包的指南
Python中引入其他包的指南 Python是一种流行的编程语言,拥有丰富的开源软件包和库。许多Python程序将使用其他包来增强其功能。在本文中,我们将探讨如何在Python项目中使用和引入其他包。 什么是Python包和库? Python包是一组可重复使用的…...

设计模式-组合模式
应用场景 实现规则匹配的逻辑 比如> <,同时支持 and or 多个条件组合 新增一个条件就增加一个实现类 说明 对于这种需要实现规则匹配的逻辑,可以考虑使用策略模式。策略模式可以将不同的算法封装成不同的策略类,让它们可以相互替换,…...
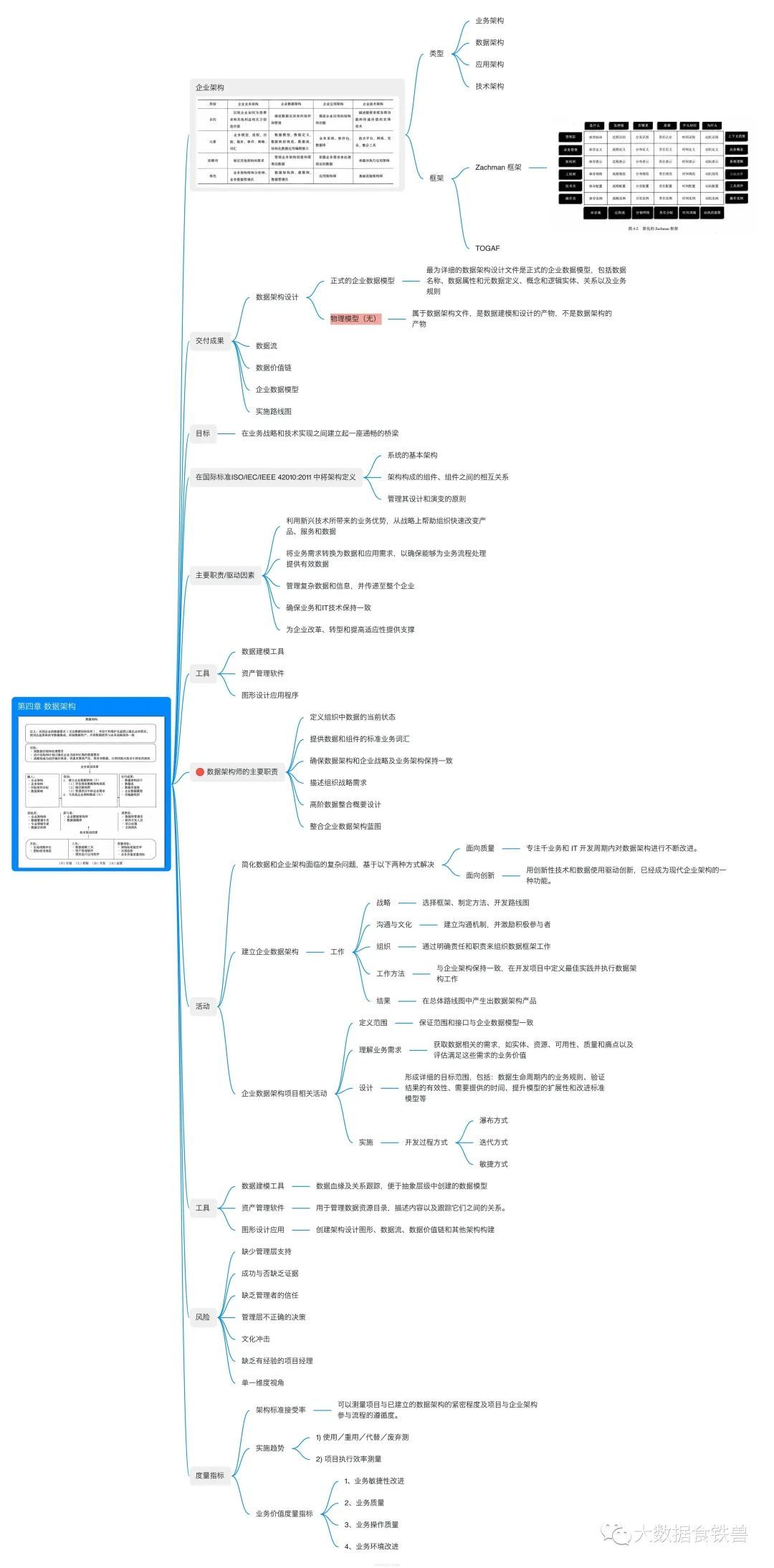
DMBOK知识梳理for CDGA/CDGP——第四章 数据架构(附常考知识点)
关 注ghz“大数据食铁兽”,回复“知识点”获取《DMBOK知识梳理for CDGA/CDGP》常考知识点(第四章 数据架构) 第四章 数据架构 第四章是CDGA|CDGP考试的重点考核章节之一,分值占比高,知识点比较密集,重点…...

MyBatisPlus总结(1.0)
MyBatis-Plus MyBatis-Plus介绍 MyBatis-Plus(简称MP)是一个MyBatis的增强工具,在MyBatis的基础上只做增强不做改变,为简化开发、提高效率而生 特性 无侵入:只做增强不做改变,引入它不会对现有工程产生影…...

职场老油条表示真干不过,部门新来的00后测试员已把我卷崩溃,想离职了...
在程序员职场上,什么样的人最让人反感呢? 是技术不好的人吗?并不是。技术不好的同事,我们可以帮他。 是技术太强的人吗?也不是。技术很强的同事,可遇不可求,向他学习还来不及呢。 真正让人反感的,是技术平平&#x…...

【每日挠头算法题(1)】——旋转字符串|亲密字符串
文章目录 一、旋转字符串思路1思路2 二、亲密字符串思路 总结 一、旋转字符串 点我直达终点~ 思路1 前提:如果s串和goal串长度不等,则goal串不可能是s串旋转得来,直接返回false; 通过观察,可以发现每旋转一次&#…...

什么是 tokens,ChatGPT里面的Tokens如何计数?
什么是 tokens,ChatGPT里面的Tokens如何计数? 什么是 tokens? Tokens 可以被认为是词语的片段。在 API 处理提示之前,输入会被分解成 tokens。这些 tokens 并不会精确地在单词的开始或结束处切分 - tokens 可以包含尾随的空格甚…...
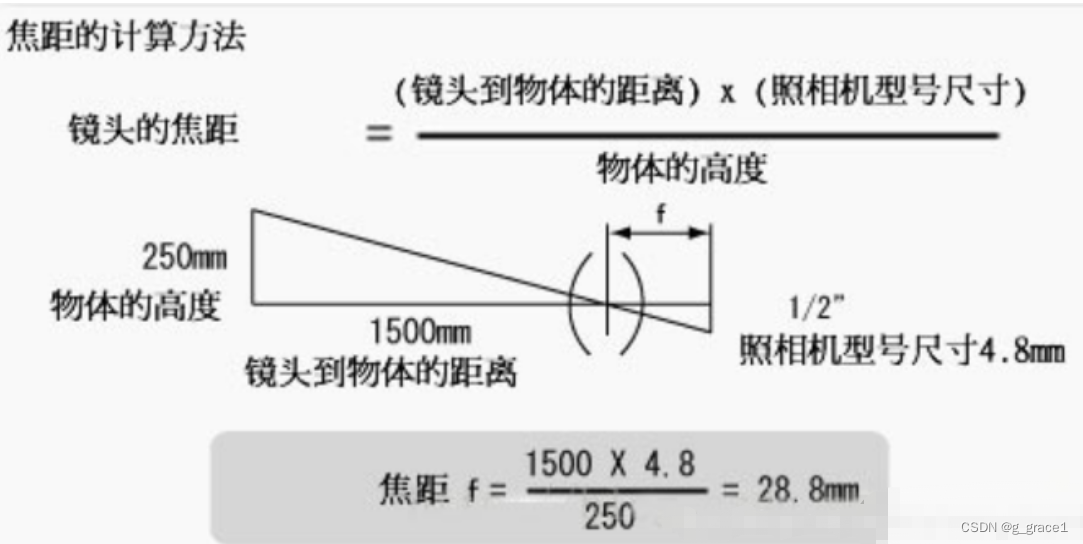
工业镜头分类、相关参数含义
一、工业镜头参数 1、焦距/后焦距 焦距是像方主面到像方焦点的距离。后焦距指光线离开镜头最后一片镜片表面到sensor感光面的距离,如8mm,16mm,25mm等; 焦距的大小决定着视角大小,焦距数值小,视角大&#…...
)
码蹄杯语言基础:数组(C语言)
码蹄集网站地址:https://www.matiji.net/exam/ojquestionlist ⭐MT1381逆序输出数组 定义一个长度为10的整型数组,输入10个数组元素的值,然后逆序输出他们 格式 输入格式: 输入10个数组元素的值,整型,空…...

DJ4-2 程序的装入和链接
目录 4.2.1 程序的装入 一、绝对装入方式 二 、可重定位装入方式 三、动态运行时装入方式 4.2.2 程序的链接 一、静态链接 二、装入时动态链接 三、运行时动态链接 在多道程序环境下,如果程序要运行,那么必须为之创建进程。而创建进程的第一件…...

开源项目合集....
likeshop开源商城系统,公众号商城、H5商城、微信小程序商城、抖音小程序商城、字节小程序商城、头条小程序商城、安卓App商城、苹果App商城代码全开源,免费商用。 适用场景:B2C商城、新零售商城、社交电商商城、分销系统商城、小程序商城、商…...
机器学习 | 降维问题
目录 一、主成分分析 二、奇异值分解 2.1 奇异值分解原理 2.2 奇异值分解实践 三、特征值与特征向量 一、主成分分析 主成分有如下特征: 每个主成分是原变量的线性组合;各个主成分之间互不相关;主成分按照方差贡献率从大到小依次排列&…...
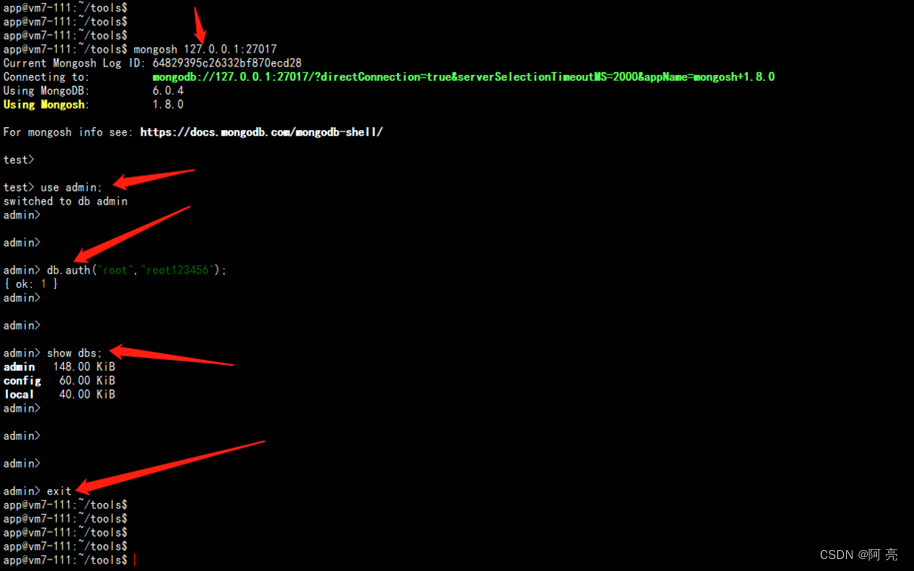
Ubuntu20.04平台下使用二进制包部署MongoDB-6.0.4单实例
文章目录 1.1 准备服务器的基本信息1.2 操作系统上创建其用户1.3 部署MongoDB服务端1.4 部署MongoDB客户端1.5 部署MongoDB 27017实例1.5.1 创建相关目录1.5.2 准备配置文件1.5.3 准备启停脚本1.5.4 进行启停测试1.5.5 加入开机自启动 1.6 创建超级管理员用户1.6.1 创建本地的超…...
Snipaste工具推荐
Snipaste Snipaste 不只是截图,善用贴图功能将帮助你提升工作效率! 新用户? 截图默认为 F1,贴图为 F3,然后请对照着 快捷键列表 按一遍,体会它们的用法,就入门啦! 遇到了麻烦&…...
MinIO快速入门——在Linux系统上安装和启动
1、简介 MinIO 是一款基于Go语言发开的高性能、分布式的对象存储系统。客户端支持Java,Net,Python,Javacript, Golang语言。MinIO系统,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等。 2、环境搭建&#…...
07.JavaWeb-Vue+elementUI
1.Vue 功能替代JavaScript和jQuery,基于JavaScript实现的前端框架 1.1配置Vue 1.1.1引入vue库 方法一:通过cdn链接引入最新版本的vue(可能会慢些) <head><script src"https://cdn.jsdelivr.net/npm/vue">…...
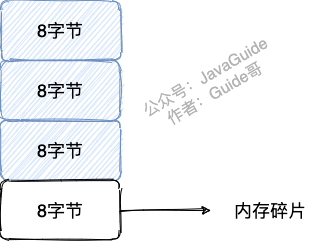
经典面试题---【第一档】
1.如果你想new一个Quene,你有几种方式?他们之间的区别是什么? 2.Redis 是如何判断数据是否过期的呢? Redis 通过一个叫做过期字典(可以看作是 hash 表)来保存数据过期的时间。过期字典的键指向 Redis 数据…...

欧美同学会第三届“双创”大赛——空天装备产业赛区(浙江诸暨)正式启动,开启报名通道
6月8日,欧美同学会第三届“双创”大赛——空天装备产业赛区(浙江诸暨)启动仪式暨北京推介会圆满举行。活动由欧美同学会(中国留学人员联谊会)主办,中共浙江省委统战部支持,浙江省欧美同学会、中…...

python3 爬虫相关学习8:python 的常见报错内容 汇总收集
目录 1 拼写错误 AttributeError: NameError: 等等 2 类型错误 TypeError: 如字符串连接错误 TypeError: can only concatenate str (not “int“) to str 3 意外缩进 IndentationError: unexpected indent 4 找不到对应模块 ModuleNotFoundError: 5 语法错误 Syntax…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
