算法模板(3):搜索(5):其他
搜索
模拟退火
- 模拟退火一个很关键的是,看看枚举到每一个方案是不是可能的。
3167. 星星还是树
- 在二维平面上有 n 个点,第 i 个点的坐标为 ( x i , y i ) (x_i,y_i) (xi,yi)。请你找出一个点,使得该点到这 n 个点的距离之和最小。
- 这个题如果是二维的话,其实是一个凸函数,我们可以用三分求解。
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<ctime>#define x first
#define y secondusing namespace std;typedef pair<double, double> P;
const int maxn = 110;
P q[maxn];
int N;
double ans = 1e8;double rand(double l, double r) {//等概率得到区间的一个点return (double)rand() / RAND_MAX * (r - l) + l;
}double get_dist(P a, P b) {double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}double calc(P p) {double res = 0;for (int i = 0; i < N; i++) {res += get_dist(q[i], p);}ans = min(ans, res);return res;
}void simulate_anneal() {P cur(rand(0, 10000), rand(0, 10000));//一开始可以把衰减系数定的大一些(0.999),边界条件定的小一些(1e-6),超时的话再调整for (double t = 1e4; t > 1e-4; t *= 0.99) {P np(rand(cur.x - t, cur.x + t), rand(cur.y - t, cur.y + t));double dt = calc(np) - calc(cur);//如果dt < 0,那么 if 里面的条件一定成立。//如果dt > 0,那么 if 里面的条件就是一个概率if (exp(-dt / t) > rand(0, 1)) cur = np;}
}int main() {scanf("%d", &N);for (int i = 0; i < N; i++) scanf("%lf%lf", &q[i].x, &q[i].y);for (int i = 0; i < 100; i++) simulate_anneal();printf("%.f\n", ans);return 0;
}
2680. 均分数据
-
已知 N N N 个正整数: A 1 、 A 2 、 … … 、 A n A_1、A_2、……、A_n A1、A2、……、An。今要将它们分成 M M M 组,使得各组数据的数值和最平均,即各组的均方差最小,其实就是每组均值的方差。均方差公式如下:
σ = ∑ i = 1 n ( x i − x ˉ ) 2 n , x ˉ = ∑ i = 1 n x i n \sigma = \sqrt{\frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n}},\bar{x} = \frac{\sum_{i=1}^n x_i}{n} σ=n∑i=1n(xi−xˉ)2,xˉ=n∑i=1nxi -
过程是这样的:
- 每次模拟退火都先随机打乱一下序列
- 每次都尝试交换序列中两个数的位置,然后贪心地分组,每次都把当前的数放到当前每组的数之和最小地组里面去,然后看均方差是否变小,用这个方式模拟退火。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<ctime>using namespace std;const int maxn = 25, maxm = 10;
int N, M;
int w[maxn], s[maxm];
double ans = 1e8;double calc() {memset(s, 0, sizeof s);for (int i = 0; i < N; i++) {int k = 0;for (int j = 0; j < M; j++) {if (s[j] < s[k]) {k = j;}}s[k] += w[i];}double avg = 0;for (int i = 0; i < M; i++) avg += (double)s[i] / M;double res = 0;for (int i = 0; i < M; i++) {res += (s[i] - avg) * (s[i] - avg);}res = sqrt(res / M);ans = min(ans, res);return res;
}void simulate_anneal() {random_shuffle(w, w + N);//最开始的t和答案的范围有关。for (double t = 1e6; t > 1e-6; t *= 0.95) {int a = rand() % N, b = rand() % N;double x = calc();swap(w[a], w[b]);double y = calc();double delta = y - x;if (exp(-delta / t) < (double)rand() / RAND_MAX) {swap(w[a], w[b]);}}
}
int main() {scanf("%d%d", &N, &M);for (int i = 0; i < N; i++) scanf("%d", &w[i]);for (int i = 0; i < 100; i++) simulate_anneal();printf("%.2f\n", ans);return 0;
}
爬山法
- 爬山法必须是凸函数,而且是单峰的。
- 既然是凸函数为什么不用三分呢?
在多年的 OI 生活中,我意识到了,人类是有极限的,无论多么工于心计,绞尽脑汁,状态总是表示不出来的,出题人的想法总是猜不透的,边界总是写不对的——所以——我不三分了 JOJO!
一维函数需要一个三分,n 维函数需要 套用 n 个三分套用,复杂度是指数级别的。——闫学灿
其实这个东西不咋考
207. 球形空间产生器
- 给一个 n 维空间的一个球,给 n + 1 个球上的点的坐标。求球心坐标。
- 这个题是可以用高斯消元写的。不过这里展现爬山法的写法。
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
using namespace std;const int maxn = 15;
int N;
double d[maxn][maxn];
double ans[maxn]; //答案,即球心坐标
double dist[maxn], delta[maxn]; //每个点到球心的距离;每一维的偏移量。void calc(){double avg = 0;for (int i = 0; i < N + 1; i++){dist[i] = delta[i] = 0;for (int j = 0; j < N; j++)//求每个点到当前球心的距离dist[i] += (d[i][j] - ans[j]) * (d[i][j] - ans[j]);dist[i] = sqrt(dist[i]);//求所有点到球心距离的均值avg += dist[i] / (N + 1);}for (int i = 0; i < N + 1; i++)for (int j = 0; j < N; j++)//这个似乎是求的梯度。delta[j] += (dist[i] - avg) * (d[i][j] - ans[j]) / avg;
}int main(){scanf("%d", &N);for (int i = 0; i <= N; i++) {for (int j = 0; j < N; j++) {scanf("%lf", &d[i][j]);//圆心先初始化为所有点的算术平均值ans[j] += (d[i][j]) / (N + 1);}}//爬山法对精度非常严格,不然可能不收敛。for (double t = 1e4; t > 1e-6; t *= 0.99997) {calc();for (int i = 0; i < N; i++)ans[i] += delta[i] * t;}for (int i = 0; i < N; i++) printf("%.3lf ", ans[i]);return 0;
}
三分和二分
三分
- 把区间砍成三份,设中间两个分界点分别为 x 1 = m 1 , x 2 = m 2 x_1 = m_1, x_2 = m_2 x1=m1,x2=m2. 从左到右三段区间记为 L 1 , L 2 , L 3 . L_1, L_2, L_3. L1,L2,L3. 这里我们假设 f ( x ) f(x) f(x) 是一个下凹的函数单峰函数,如果是上凸的函数,要学会转化。
- 那么,有两种情况:
- 若 f ( m 1 ) < f ( m 2 ) f(m1) < f(m2) f(m1)<f(m2),那么极值点一定不在 L 3 L_3 L3 这个区间,可以舍掉 L 3 L_3 L3.
- 若 f ( m 1 ) ≥ f ( m 2 ) f(m1) \ge f(m2) f(m1)≥f(m2),那么极值点一定不在 L 1 L_1 L1 这个区间,可以舍掉 L 1 L_1 L1.
浮点数三分
- 注:这个是有 f f f 极小值的情况。
const double eps = 1e-8;
double f(m){//这里返回函数f(m)的值
}
double ternary_search(double l, double r){while(r - l > eps){double m1 = (l + r) / 2;double m2 = (m1 + r) / 2;if(f(m1) < f(m2)) r = m2;else l = m1;}return f(l);
}
整数三分
- 注:这个是 f f f 有极小值的情况。
double f(m){//这里返回函数f(m)的值
}
int ternary_search(int lb, int ub){while (ub - lb > 1) {ll m1 = (lb + ub) / 2;ll m2 = (m1 + ub) / 2;ll f1 = f(m1), f2 = f(m2);if (f1 > f2) lb = m1;else ub = m2;}return min(f(lb), f(ub));
}
- 上面板子似乎有边界问题,我改了改
ll ternary_search() {ll lb = -2e17, ub = 2e17;ll res = min(f(lb), f(ub));while (ub >= lb) {ll m1 = (lb + ub) / 2;ll m2 = (m1 + ub) / 2;if (f(m1) >= f(m2)) lb = m1 + 1;else ub = m2 - 1;res = min(res, min(f(m1), f(m2)));res = min(res, min(f(lb), f(ub)));}return res;
}
二分
整数二分新写法
bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid; // check()判断mid是否满足性质else l = mid + 1;}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}
相关文章:
:搜索(5):其他)
算法模板(3):搜索(5):其他
搜索 模拟退火 模拟退火一个很关键的是,看看枚举到每一个方案是不是可能的。 3167. 星星还是树 在二维平面上有 n 个点,第 i 个点的坐标为 ( x i , y i ) (x_i,y_i) (xi,yi)。请你找出一个点,使得该点到这 n 个点的距离之和最小。这…...
AWS CodeWhisperer 心得体会:安装与使用
大家好,今天我要和大家分享一下我在使用 AWS CodeWhisperer 这个工具时的心得体会。首先,让我们了解一下什么是 AWS CodeWhisperer。 什么是 AWS CodeWhisperer? AWS CodeWhisperer 是一个用于帮助开发者在 AWS 云平台上更轻松地编写、测试…...

高级查询 — 子查询
关于嵌套查询(子查询) 1.概述 子查询是在一个查询中嵌套另一个查询的查询语句。内部查询从外部查询或数据库中提取数据,然后使用这些数据来执行内部查询。出现在其他语句中的 select 语句,称为嵌套查询或子查询。外部的查询语句…...

霍夫变换(Hough Transform)
文章目录 1. 什么是霍夫变换2. 霍夫直线检测2.1 霍夫直线检测的具体步骤2.2 霍夫直线检测的优缺点2.3 OpenCV中霍夫直线检测的应用2.3.1 标准霍夫检测2.3.2 概率霍夫检测 3. 霍夫圆检测4. 源码仓库地址 1. 什么是霍夫变换 霍夫变换(Hough Transform)是图像处理中的一种特征提取…...

【每日挠头算法题(2)】压缩字符串|仅执行一次字符串交换能否使两个字符串相等
文章目录 一、压缩字符串思路 二、仅执行一次字符串交换能否使两个字符串相等思路1:计数法思路2:模拟法 总结 一、压缩字符串 点我直达~ 思路 使用双指针法 大致过程如下: 使用双指针,分别读(read)&…...

V4L2框架解析
和你一起终身学习,这里是程序员Android 经典好文推荐,通过阅读本文,您将收获以下知识点: 一、概览二、流程简介三、关键结构体四、模块初始化五、处理用户空间请求 一、概览 相机驱动层位于HAL Moudle与硬件层之间,借助linux内核驱…...
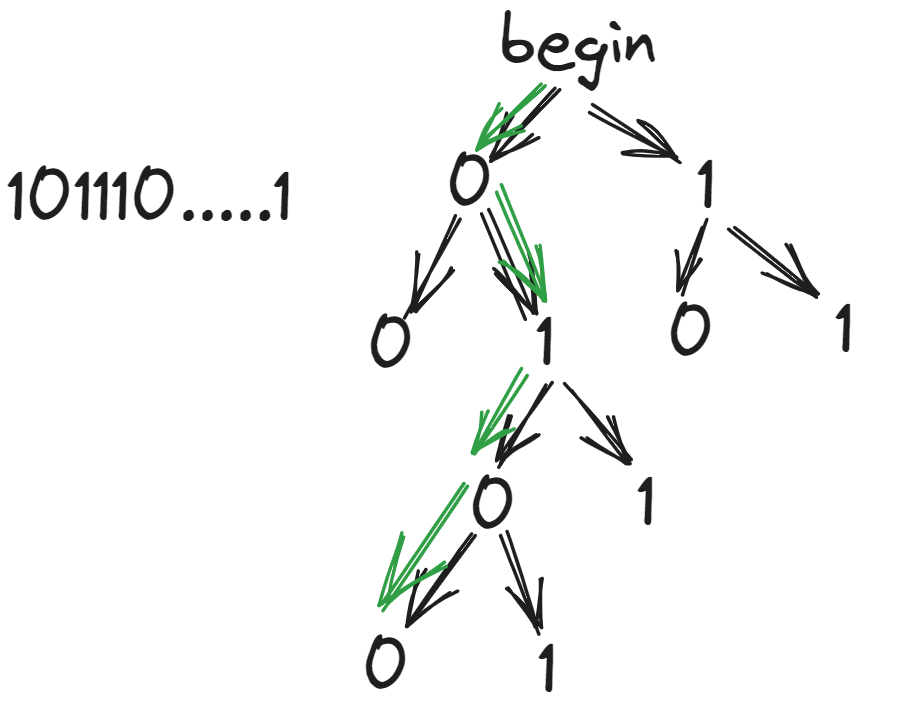
Trie树模板与应用
文章和代码已经归档至【Github仓库:https://github.com/timerring/algorithms-notes 】或者公众号【AIShareLab】回复 算法笔记 也可获取。 文章目录 Trie树(字典树)基本思想例题 Trie字符串统计code关于idx的理解 模板总结应用 最大异或对分…...
)
【华为OD统一考试B卷 | 200分】跳格子游戏(C++ Java JavaScript Python)
文章目录 题目描述输入描述输出描述用例C++javajavaScriptpython题目描述 地上共有N个格子,你需要跳完地上所有的格子,但是格子间是有强依赖关系的,跳完前一个格子后,后续的格子才会被开启,格子间的依赖关系由多组steps数组给出,steps[0]表示前一个格子,steps[1]表示st…...

该选哪个语言进修呢?
前言: 如今,计算机编程已经成为了许多工作领域中的必备技能。但是,现在的计算机语言有很多,这可能会让我们感到困惑:我应该从哪个语言开始呢?在这篇博客中,我们将详细分析当前流行的一些计算机…...

数据库实验三 数据查询一
任务描述 本关任务:按条件查询数据表的所有字段 为了完成本关任务,你需要掌握: 如何查询数据表的所有字段 相关知识 查询数据表 命令格式: select * from 数据表 where 查询条件 任务要求 打开province数据库 第一题 查询街…...

【Python百日进阶-Web开发-Peewee】Day244 - 数据库 Postgresql、CockroachDB
文章目录 六、数据库6.1 初始化数据库6.2 使用 Postgresql6.2.1 隔离级别 6.3 使用 CockroachDB 六、数据库 http://docs.peewee-orm.com/en/latest/peewee/database.html PeeweeDatabase对象表示与数据库的连接。该类Database使用打开数据库连接所需的所有信息进行实例化&…...

Vue 中的列表渲染
Vue 中的列表渲染 在 Vue 中,列表渲染是非常常见的操作。它允许我们将一个数组中的数据渲染为一个列表,从而实现数据的展示和交互。在本文中,我们将探讨 Vue 中的列表渲染的基本原理和用法,并给出一些实例代码来帮助读者更好地理…...

java 中的关键字
1. 面向对象编程(OOP) - 把程序中的实体看做对象,而不是过程或函数。OOP有3个基本特征:封装,继承和多态。 2. 类(Class) - 一个用于描述对象属性和方法的蓝图。 3. 对象(Object) - 类的实例化,也就是一个具体的实体。 4. 方法(Met…...

python序列化和结构化数据详解
序列化和结构化数据是计算机程序中非常重要的概念,它们的原理和应用在许多应用程序中都是必不可少的。Python作为一种高级编程语言,在序列化和结构化数据方面提供了很多优秀的解决方案。在本文中,我们将详细介绍Python中序列化和结构化数据的…...
PoseiSwap的趋势性如何体现?
DEX 代表了一种先进的意识形态,相对于 CEX 其更强调无许可、去中心化以及公开透明。然而随着 DeFi 赛道逐渐从 2021 年年底的高峰逐渐转向低谷,DEX 整体的交易量、TVL等数据指标也开始呈现下滑的趋势,DEX 正在面临发展的新瓶颈期。 在这样的背…...
西南交通大学智能监测 培训课程练习4
2023.056.07和09培训 项目实战 目录 一、infracore(基础核心层) 1.1database 1.2config 1.3util 二、业务领域模块 2.1structure模块 2.1.1domain层 2.1.2application层 2.1.3adapter层 2.2sensor模块 2.2.1domian层 2.2.2application层 2.2.…...
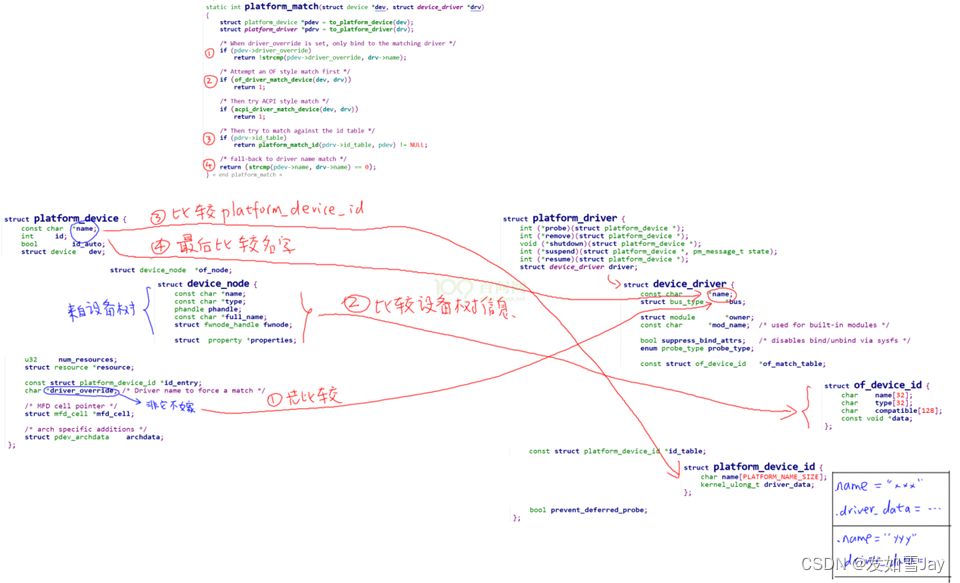
设备树的引入及简明教程
首先说明,设备树不可能用来写驱动。 设备树只是用来给内核里的驱动程序,指定硬件的信息。比如LED驱动,在内核的驱动程序里去操作寄存器,但是操作哪一个引脚?这由设备树指定。 需要编写设备树文件(dts: device tree s…...

MM32F3273G8P火龙果开发板MindSDK开发教程12 -获取msa311加速器的敲击事件
MM32F3273G8P火龙果开发板MindSDK开发教程12 -获取msa311加速器的敲击事件 1、功能描述 msa311可以识别单击、双击事件,类似手机上的点击返回,双击截屏功能。 单击,双击都能产生中断事件。 中断事件产生后,从对应的状态寄存器读…...

Maven聚合
在实际的开发过程中,我们所接触的项目一般都由多个模块组成。在构建项目时,如果每次都按模块一个一个地进行构建会十分得麻烦,Maven 的聚合功能很好的解决了这个问题。 聚合 使用 Maven 聚合功能对项目进行构建时,需要在该项目中…...
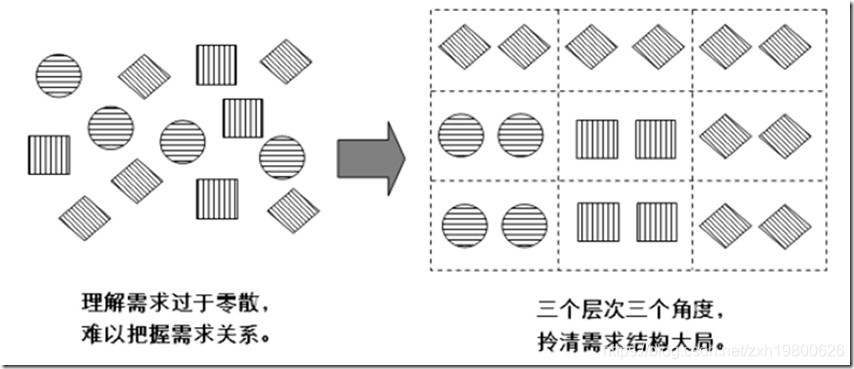
[架构之路-211]- 需求- 软架构前的需求理解:ADMEMS标准化、有序化、结构化、层次化需求矩阵 =》需求框架
目录 前言: 一、什么是ADMES: 首先,需求是分层次的: 其次,需求是有结构的,有维度的 再次,不同层次需求、不同维度需求之间可以相互转化(难点、经验积累) 最终,标准…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
