chatgpt赋能python:Python实现Fibonacci数列
Python实现Fibonacci数列
Fibonacci数列是一个非常经典的数列,定义如下:
F ( 0 ) = 0 , F ( 1 ) = 1 F(0)=0, F(1)=1 F(0)=0,F(1)=1
F ( n ) = F ( n − 1 ) + F ( n − 2 ) F(n)=F(n-1)+F(n-2) F(n)=F(n−1)+F(n−2)
也就是说,第n个数等于前两个数之和。 著名的比如,0、1、1、2、3、5、8、13、21、34、……
在Python中,我们可以通过递归和循环两种方式来实现Fibonacci数列。
递归实现
首先,我们来看递归实现。
def fib_recursion(n):if n < 2:return nreturn fib_recursion(n-1) + fib_recursion(n-2)
这个代码比较简单,当n小于2时,返回n。否则,返回前两项的和。但是,递归实现的问题在于,它的时间复杂度非常高。如果你调用fib_recursion(50),它会非常慢。
循环实现
循环实现是避免递归缺点的一个途径。
def fib_loop(n):if n == 0:return 0elif n == 1:return 1f0, f1 = 0, 1for i in range(2, n+1):f0, f1 = f1, f0+f1return f1
这个实现的思路是,如果n=0或1,返回0或1。否则,用循环来计算前两项的和,直到n。
由于循环实现不涉及函数调用,因此它比递归实现要快得多。再次对比,如果你调用fib_loop(50),结果几乎是立即得出的。
结论
综合来看,循环实现更高效,但也可以看到递归实现的写法更简洁。在实际应用中,要根据具体情况选择算法,用最优的方式来解决问题。
最后的最后
本文由chatgpt生成,文章没有在chatgpt生成的基础上进行任何的修改。以上只是chatgpt能力的冰山一角。作为通用的Aigc大模型,只是展现它原本的实力。
对于颠覆工作方式的ChatGPT,应该选择拥抱而不是抗拒,未来属于“会用”AI的人。
🧡AI职场汇报智能办公文案写作效率提升教程 🧡 专注于AI+职场+办公方向。
下图是课程的整体大纲
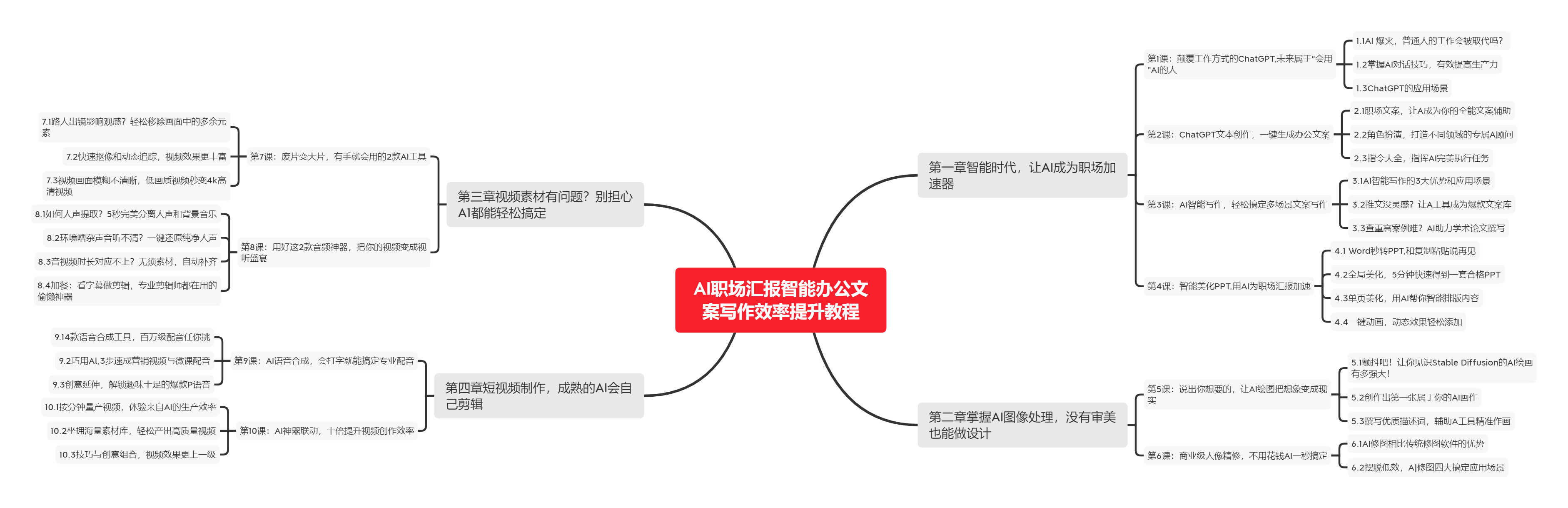

下图是AI职场汇报智能办公文案写作效率提升教程中用到的ai工具

🚀 优质教程分享 🚀
- 🎄可以学习更多的关于人工只能/Python的相关内容哦!直接点击下面颜色字体就可以跳转啦!
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| 🧡 AI职场汇报智能办公文案写作效率提升教程 🧡 | 进阶级 | 本课程是AI+职场+办公的完美结合,通过ChatGPT文本创作,一键生成办公文案,结合AI智能写作,轻松搞定多场景文案写作。智能美化PPT,用AI为职场汇报加速。AI神器联动,十倍提升视频创作效率 |
| 💛Python量化交易实战 💛 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
| 🧡 Python实战微信订餐小程序 🧡 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
相关文章:

chatgpt赋能python:Python实现Fibonacci数列
Python实现Fibonacci数列 Fibonacci数列是一个非常经典的数列,定义如下: F ( 0 ) 0 , F ( 1 ) 1 F(0)0, F(1)1 F(0)0,F(1)1 F ( n ) F ( n − 1 ) F ( n − 2 ) F(n)F(n-1)F(n-2) F(n)F(n−1)F(n−2) 也就是说,第n个数等于前两个数之和…...

开环模块化多电平换流器仿真(MMC)N=6
模型简介: 运行环境MATLAB2021a 开环模块化多电平换流器仿真(MMC)N=6,连接负载,采用载波移相调制。 可以得到换流器输出N+1=7电平的相电压波形。可考虑线路阻抗。 子模块采用半桥结…...
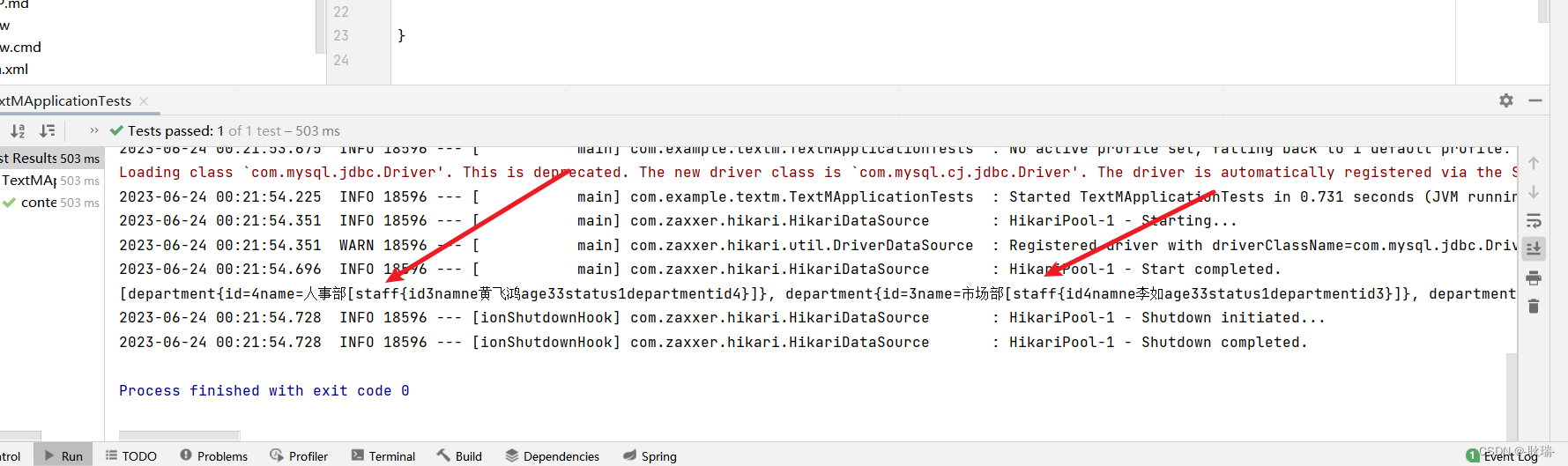
java springboot整合MyBatis联合查询
前面文章 java springboot整合MyBatis做数据库查询操作写了springboot整合MyBatis的方法 并演示了基础查询的语法 根据id查 那么 我们这次来演示联合查询 我们staff 表 内容如下 每条数据 对应的都有一个departmentid 这是 department部门表的外键id department表内容如下 如…...
windows2022证书配置.docx
Windows证书的配置 要求两台主机,一台作为域,一台进入域 按要求来选择角色服务 确认之后安装 安装完以后配置证书服务 选择服务 按要求配置 注:此处不用域用户登陆无法使用企业CA 按要求来 创建新的私钥 这几处检查无误后默认即可 有效期…...
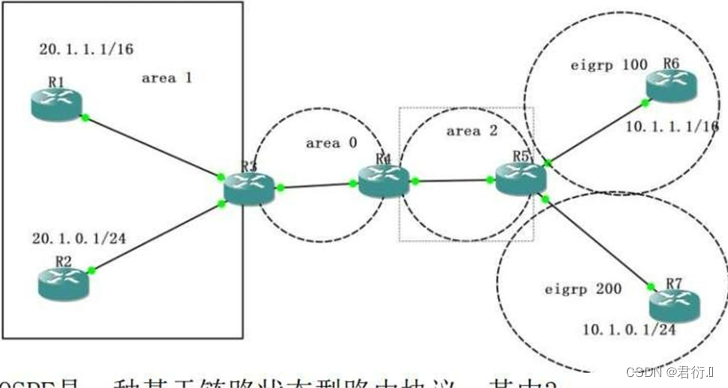
HCIP网络笔记分享——IA回顾及OSPF协议
第一部分 HCIA回顾1、网络基础2、动态路由协议3、路由认证4、路由控制(AD metric ) 一、知识巩固二、场景模拟1、获取IP地址1.1 DHCP --- 动态主机配置协议1.1.1 DHCP客户端1.1.2 DHCP服务器1.1.3 DHCP客户端1.1.4 DHCP服务器 2、打开浏览器3、路由器进行…...
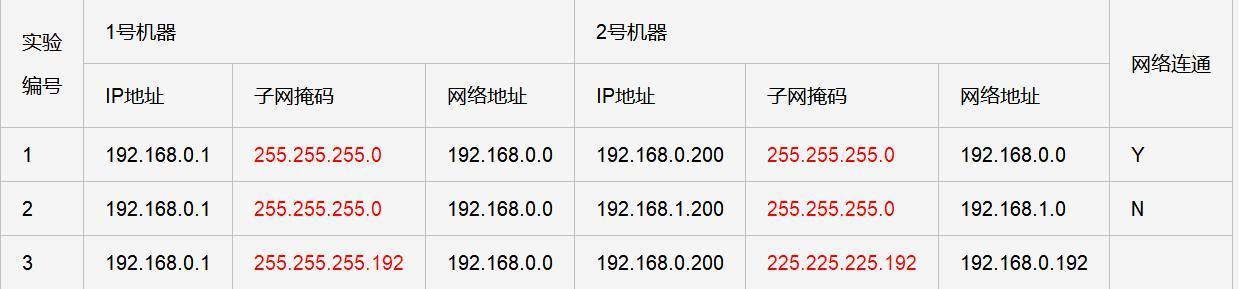
网络:IP地址、子网掩码、网络地址、广播地址、网段、网关
目录 一、IP地址 二、子网掩码 三、网络地址 四、广播地址 五、网段 六、网关 七、IP地址、子网掩码、网络地址、广指地址、网殷、网关的关系 参考链接 一、IP地址 IP地址是因特网协议(IP)中使用的一种数字标识符,用于唯一地标识网络…...
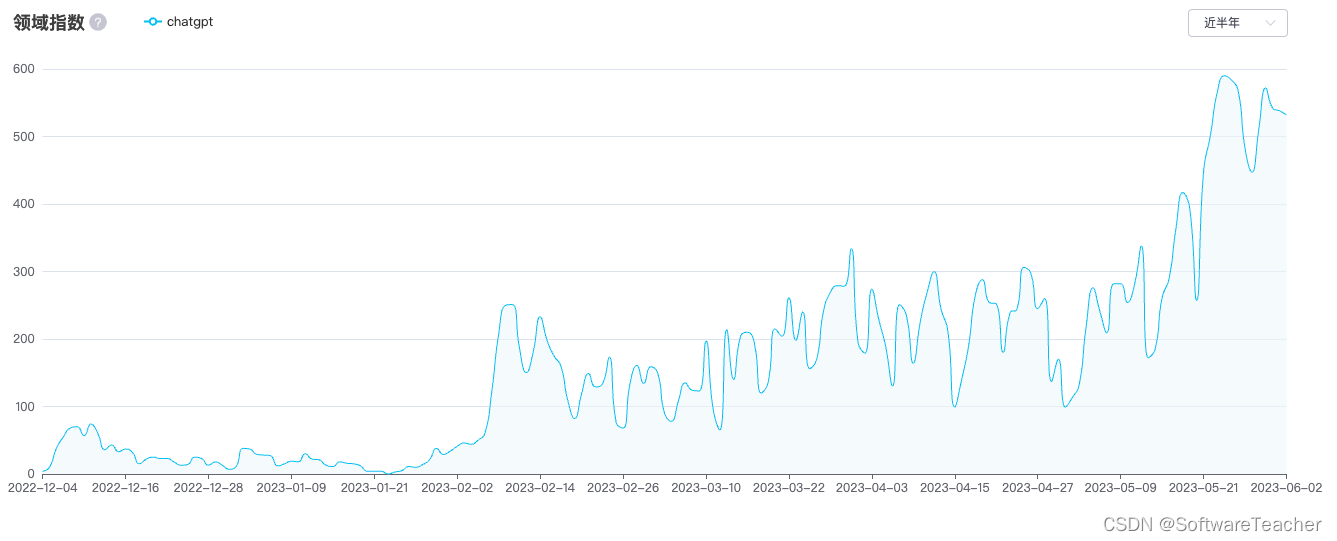
编程的未来 - 还有未来么?
缘起 唐门教主上个月某天深夜写了一篇博客 --《编程的未来》,要我谈谈感想。 这也是最近软件工程师们聊得比较多的问题,上周,在上海的 “关东小磨” 和十多位 CSDN 博主聚会的时候,大家也稍微谈了一下这个话题,但是谈…...
)
从零开始搭建群众权益平台(二)
这篇文章我们要建立的群众权益维护平台需要提供用户注册、登录、提交和查看问题或建议的功能,并且支持电话短信登录。在这个过程中,我们需要存储用户的登录信息。 我们将使用Node.js和Express.js作为后端框架,MongoDB作为数据库,并且使用Twilio服务发送短信验证码来实现手…...

Mysql之数据备份
一.日志 1.MySQL 的日志默认保存位置为 /usr/local/mysql/data2.修改日志配置文件 vim /etc/my.cnf [mysqld] ##错误日志,用来记录当MySQL启动、停止或运行时发生的错误信息,默认已开启 log-error/usr/local/mysql/data/mysql_error.log #指定日志的…...
【数据库数据恢复】SQL Server数据表结构损坏的数据恢复案例
数据库故障&分析: SQL server数据库数据无法读取。 经过初检,发现SQL server数据库文件无法被读取的原因是因为底层File Record被截断为0,无法找到文件开头,数据表结构损坏。镜像文件的前面几十M空间和中间一部分空间被覆盖掉…...
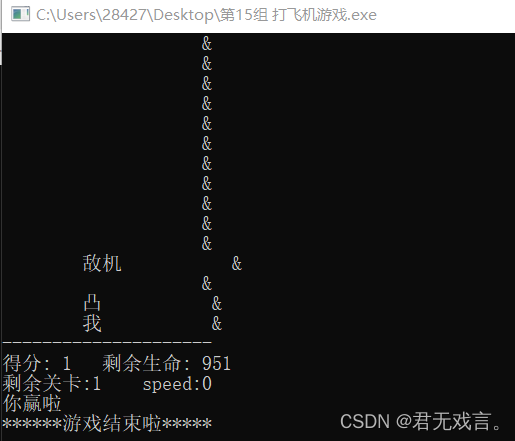
C语言/C++ 之 打飞机游戏
【项目简介】 1、设计思想:本项目主要是为了实现打飞机游戏,主要包括5个函数模块,和1个主函数框架。分别是chu_shi_hua();、you_cao_zuo;、wu_cao_zuo();、show();、main();等。项目完成过程中主要运用了C/C中的输入输…...

在 Docker 中部署 Mino 并挂载配置文件
创建本地目录 首先,在主机上创建一个目录,用于存放 Mino 的配置文件。例如,创建一个名为 mino 的目录,用于存放 Mino 的配置文件。 mkdir mino拉取 Mino 镜像 使用以下命令从 Docker Hub 上拉取 Mino 的最新镜像: …...

无限脉动:释放音乐和区块链在音乐领域的力量
音乐是一种永恒的通用语言,它将人们聚集在一起,超越了边界,在我们灵魂深处产生共鸣,创造联系。在当今数字时代,随着区块链技术和去中心化网络的出现,音乐世界正在经历一场深刻的变革。 我们在与艺术家合作&…...
读发布!设计与部署稳定的分布式系统(第2版)笔记09_一窝蜂和容量
1. 停电事故后电力恢复的方式 1.1. 停电后常见的情形是,送电几秒钟后又再次断电 1.2. 数百万台空调和冰箱的用电需求,使刚刚恢复的电力供应发生过载 1.3. 当电力供应不足时,增加的电流很快就到达满负荷,导致过载,触…...

详解java定时任务
在我们编程过程中如果需要执行一些简单的定时任务,无须做复杂的控制,我们可以考虑使用JDK中的Timer定时任务来实现。下面LZ就其原理、实例以及Timer缺陷三个方面来解析java Timer定时器。 一、简介 在java中一个完整定时任务需要由Timer、TimerTask两个…...

PCIe卡设计方案:单路12Gsps 3G 带宽模拟信号源PCIe卡
一、板卡概述 单路3G带宽模拟信号源卡由DA子卡和PCIe底板组成,二者通过标准FMC连接器互联,可以实现将PCIe总线数据转换为一路高速的模拟量输出。北京太速科技板可广泛用于雷达、通信、光电领域的噪声信号、毛刺、脉冲信号模拟产生等领域。 二、 …...

第1章 计算机网络和因特网
1、主机或端系统通过( )接入因特网。 A. ISPB. 调制解调器C. 交换机D. 路由器 P21:端系统(PC、智能手机、Web 服务器、电子邮件服务器等)经过一个接入 ISP 与因特网相连。 2、主机一般被划分为两类:客…...
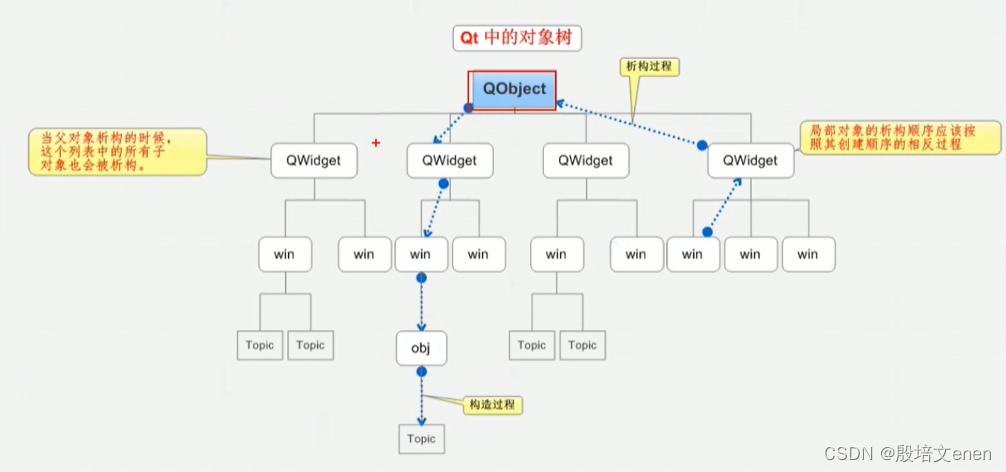
QT入门基础知识
什么是QT QT是一个跨平台的C图像用户界面应用程序框架QT在1991年由奇趣科技开发QT的优点 跨平台,几乎支持所有平台接口简单,容易上手一定程度上简化了内存回收机制有很好的社区氛围可以进行嵌入式开发 QWidget QT注意事项 命名规范 类名 首字母大写,单…...
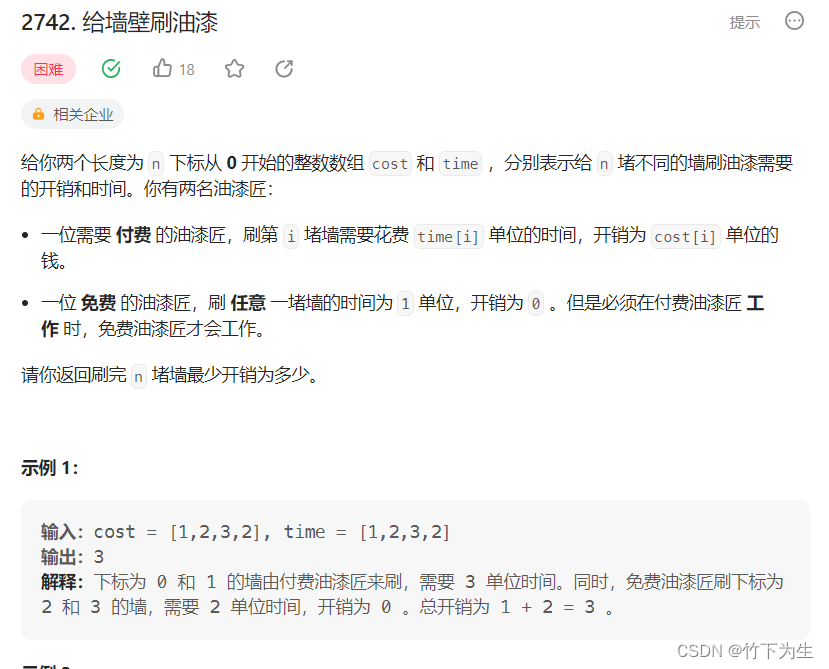
Leetcode---350周赛
题目列表 6901. 总行驶距离 6890. 找出分区值 6893. 特别的排列 6447. 给墙壁刷油漆 一、总行驶距离 很显然,这题单纯就是一道数学应用题,我们要明白最关键的一点 :只有当mainTank>5并且additionalTank>0时,才能发生副油…...

Django通过Nginx和uWSGI实现负载均衡
Django是一款非常流行的Web应用程序框架,它允许开发人员以快速、简单和灵活的方式构建可扩展和可维护的Web应用程序。当你的应用程序开始变得越来越受欢迎时,你可能会发现需要使用负载均衡来确保应用程序的可用性和性能。在本文中,我们将介绍…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
