P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷
P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷
洛谷题目传送门
文章目录
- P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 题目大意
- 方法一(线段树维护dp)
- code
- 方法二 (单调队列维护dp)
- code
题目描述
In an ill-conceived attempt to enhance the mobility of his prize cow Bessie, Farmer John has attached a pogo stick to each of Bessie’s legs. Bessie can now hop around quickly throughout the farm, but she has not yet learned how to slow down.
To help train Bessie to hop with greater control, Farmer John sets up a practice course for her along a straight one-dimensional path across his farm. At various distinct positions on the path, he places N targets on which Bessie should try to land (1 <= N <= 1000). Target i is located at position x(i), and is worth p(i) points if Bessie lands on it. Bessie starts at the location of any target of her choosing and is allowed to move in only one direction, hopping from target to target. Each hop must cover at least as much distance as the previous hop, and must land on a target.
Bessie receives credit for every target she touches (including the initial target on which she starts). Please compute the maximum number of points she can obtain.
FJ给奶牛贝西的脚安装上了弹簧,使它可以在农场里快速地跳跃,但是它还没有学会如何降低速度。
FJ觉得让贝西在一条直线的一维线路上进行练习,他在不同的目标点放置了N (1 <= N <= 1000)个目标点,目标点i在目标点x(i),该点得分为p(i)。贝西开始时可以选择站在一个目标点上,只允许朝一个方向跳跃,从一目标点跳到另外一个目标点,每次跳跃的距离至少和上一次跳跃的距离相等,并且必须跳到一个目标点。
每跳到一个目标点,贝西可以拿到该点的得分,请计算他的最大可能得分。
输入格式
* Line 1: The integer N.
* Lines 2…1+N: Line i+1 contains x(i) and p(i), each an integer in the range 0…1,000,000.
输出格式
* Line 1: The maximum number of points Bessie can receive.
样例 #1
样例输入 #1
6
5 6
1 1
10 5
7 6
4 8
8 10
样例输出 #1
25
提示
There are 6 targets. The first is at position x=5 and is worth 6 points, and so on.
Bessie hops from position x=4 (8 points) to position x=5 (6 points) to position x=7 (6 points) to position x=10 (5 points).
题目大意
草场上有一条直线,直线上有若干个目标点。每个目标点都有一个分值和一个坐标。现在你可以选择其中任意一个目标点开始跳,只能沿一个方向跳,并且必须跳到另一个目标点。且每次跳的距离都不能少于上一次的距离。请问你能得到的最大分值是多少?、
方法一(线段树维护dp)
考试时就是想到了这个做法,但是改了时限100ms过不了
设 f i , j f_{i , j} fi,j 表示只通过 j j j 步到达点 i i i 的最大分值。
j j j 会炸空间?
j j j 其实最多只有 n 2 n^2 n2 种可能,乱搞一下就好了
那么:
f i , j = M a x k = 1 i − 1 ( M a x l = 0 j f k , l + p i ) f_{i , j} = Max_{k = 1}^{i - 1}(Max_{l = 0}^jf_{k , l} + p_i) fi,j=Maxk=1i−1(Maxl=0jfk,l+pi)
用线段树维护一下 f k , l f_{k , l} fk,l 就好了
code
#include <bits/stdc++.h>
#define fu(x, y, z) for (int x = y; x <= z; x++)
#define fd(x, y, z) for (int x = y; x >= z; x--)
#define LL long long
using namespace std;
const int N = 1005, M = 1000005;
struct node {int x, p;
} t[N];
LL ans;
int n, cnt, flg[M], p[M], p1[M], K = 1000005, len, dis[N][N];
struct Tr {LL val;int lp, rp;
} tr[M * 8];
bool cmp(node x, node y) { return x.x < y.x; }
void glp(int x) { tr[x].lp = ++len; }
void grp(int x) { tr[x].rp = ++len; }
void updata(int x) { tr[x].val = max(tr[tr[x].lp].val, tr[tr[x].rp].val); }
void change(int x, int l, int r, int pos, LL v) {if (l == r)tr[x].val = max(tr[x].val, v);else {int mid = l + r >> 1;if (pos <= mid) {if (!tr[x].lp)glp(x);change(tr[x].lp, l, mid, pos, v);} else {if (!tr[x].rp)grp(x);change(tr[x].rp, mid + 1, r, pos, v);}updata(x);}
}
int query(int x, int l, int r, int pos) {if (r <= pos)return tr[x].val;else {int mid = l + r >> 1, max1 = 0, max2 = 0;if (tr[x].lp)max1 = query(tr[x].lp, l, mid, pos);if (mid < pos && tr[x].rp)max2 = query(tr[x].rp, mid + 1, r, pos);return max(max1, max2);}
}
void clear(int x) {if (tr[x].lp)clear(tr[x].lp);if (tr[x].rp)clear(tr[x].rp);tr[x].val = tr[x].lp = tr[x].rp = 0;
}
void fans() { fu(i, 1, n) ans = max(ans, tr[i].val); }
int main() {scanf("%d", &n);fu(i, 1, n) scanf("%d%d", &t[i].x, &t[i].p);sort(t + 1, t + n + 1, cmp);fu(i, 1, n) fu(j, 1, n) dis[i][j] = abs(t[i].x - t[j].x);fu(i, 1, n) fu(j, 1, n) {if (!flg[dis[i][j]]) {flg[dis[i][j]] = 1;p[++cnt] = dis[i][j];K = max(K, dis[i][j]);}}sort(p + 1, p + cnt + 1);fu(i, 1, cnt) p1[p[i]] = i;len = n;fu(i, 1, n) {ans = max(ans, 1ll * t[i].p);change(i, 0, K, p1[0], 1ll * t[i].p);}int k, k2;fu(i, 1, n) {fu(j, 1, i - 1) {k = query(j, 0, K, p1[dis[i][j]]);k2 = query(i, 0, K, p1[dis[i][j]]);if (k + t[i].p > k2)change(i, 0, K, p1[dis[i][j]], k + t[i].p);}}fans();fu(i, 1, n) clear(i);len = n;fu(i, 1, n) change(i, 0, K, p1[0], t[i].p);fd(i, n, 1) {fd(j, n, i + 1) {k = query(j, 0, K, p1[dis[i][j]]);k2 = query(i, 0, K, p1[dis[i][j]]);if (k + t[i].p > k2)change(i, 0, K, p1[dis[i][j]], k + t[i].p);}}fans();printf("%lld", ans);
}
然后因为查找函数没有加等号 , 就寄掉8分。
差点就AK了

方法二 (单调队列维护dp)
设 f i , j f_{i , j} fi,j 表示从 j j j 到 i i i 的最大分值 , 用单调队列维护
好像宏定义会慢一点?
code
#include <bits/stdc++.h>
#define LL long long
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
const int N = 2005;
struct node {int x , p;
} t[N];
int n , k;
LL ans , f[N][N];
inline bool cmp (node x , node y) { return x.x < y.x; }
inline bool cmp1 (node x , node y) { return x . x > y.x; }
inline void fans (int flg) {memset (f , -0x3f , sizeof (f));if (flg == 1) sort (t + 1 , t + n + 1 , cmp);else sort (t + 1 , t + n + 1 , cmp1);for (int j = 1 ; j <= n ; j ++) {f[j][j] = t[j].p;for (int i = j + 1 , k = j + 1 ; i <= n ; i ++) {f[i][j] = f[i - 1][j] - t[i - 1].p;while (k > 1 && (t[j].x - t[k - 1].x) * flg <= (t[i].x - t[j].x )* flg)f[i][j] = max (f[i][j] , f[j][--k]);f[i][j] += t[i].p;ans = max (ans , f[i][j]);}ans = max (ans , f[j][j]);}
}
int main () {scanf ("%d" , &n);fu (i , 1 , n) scanf ("%d%d" , &t[i].x , &t[i].p);sort (t + 1 , t + n + 1 , cmp);fans (1);fans (-1);printf ("%lld" , ans);return 0;
}
相关文章:

P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷
P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷 洛谷题目传送门 文章目录 P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示题目大意方法一(线段树维护dp)code 方法二 (单调队列维护dp&…...
计算机网络 - 第一章(下)
1.2_1 分层结构、协议、接口、服务_哔哩哔哩_bilibili1.2_1 分层结构、协议、接口、服务是王道计算机考研 计算机网络的第7集视频,该合集共计76集,视频收藏或关注UP主,及时了解更多相关视频内容。https://www.bilibili.com/video/BV19E411D78…...

【Uniapp】小程序携带Token请求接口+无感知登录方案2.0
本次改进原文《【Uniapp】小程序携带Token请求接口无感知登录方案》,在实际使用过程中我发现以下bug: 若token恰好在用户访问接口时到期,就会直接查询为空,不反映token过期问题(例如:弹窗显示订单查询记录…...
Ubuntu常用命令
文章目录 1:文件管理2:文档编辑3:系统管理4:磁盘管理5:文件传输6:网络通讯7:设备管理8:备份压缩9:其他命令扩展:知识干货 1:文件管理 ls命令 –…...
ERP重构-SLA子分类账-分布式实现方案
背景 ERP中的GL总账模块,明细数据来源于各个业务模块如库存、成本、应收、应付、费控、资产等,统称为子模块,生成的账叫做子分类账。然而记账的业务逻辑各式各样,但是最终输出都是来源、类型、期间、科目、借贷金额等等关键信息。…...

IP路由协议(RIP、IGRP、OSPF、IS-IS、BGP)
文章目录 1、路由分类2、RIP协议1)RIP的工作原理2)RIP路由表的更新过程3)RIP路由表的更新原则4)RIP的特性5)RIP协议的版本 4、IGRP协议1)IGRP路由表的更新2)IGRP的度量标准 5、OSPF协议1&#x…...
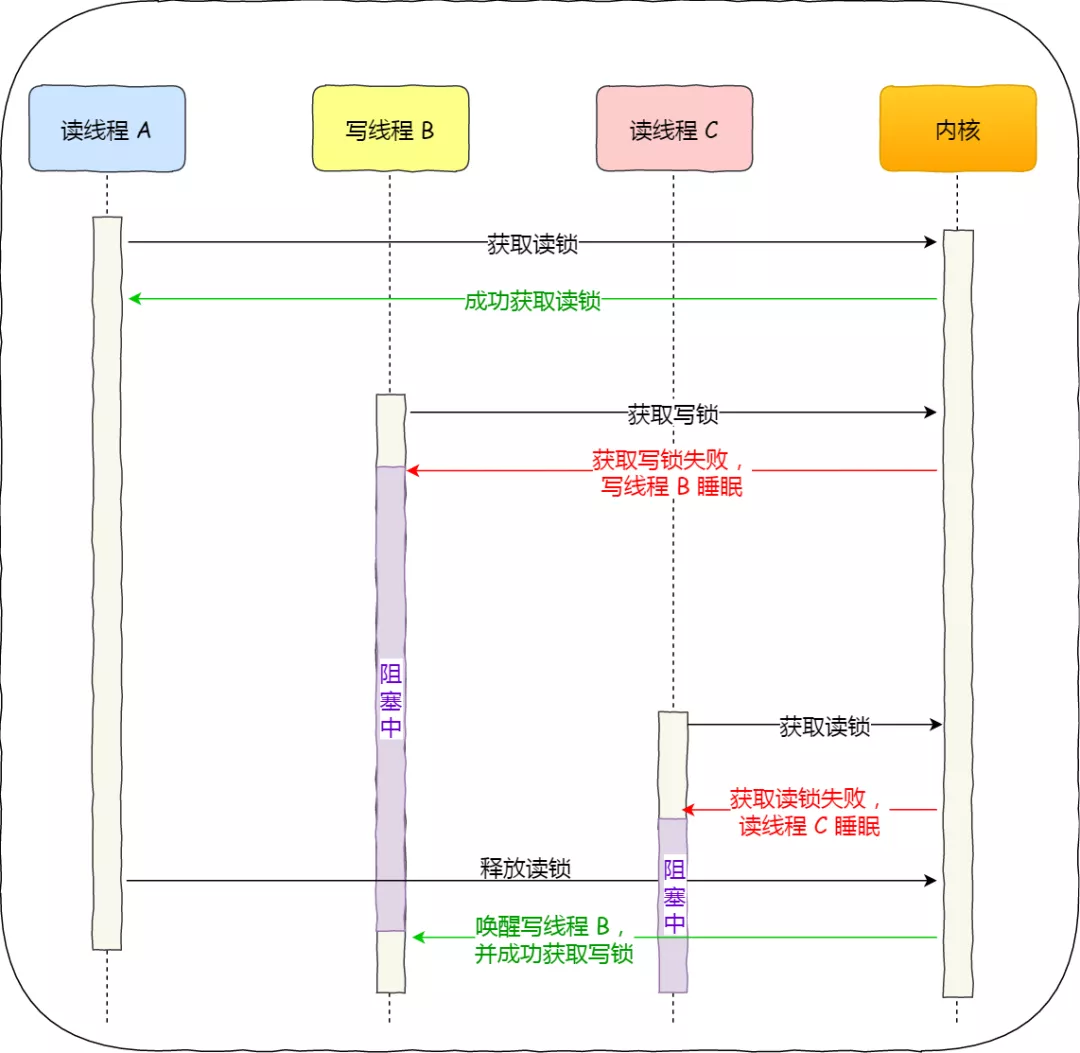
互斥锁、自旋锁、读写锁、悲观锁、乐观锁的应用场景
多线程访问共享资源的时候,避免不了资源竞争而导致数据错乱的问题,所以我们通常为了解决这一问题,都会在访问共享资源之前加锁。 最常用的就是互斥锁,当然还有很多种不同的锁,比如自旋锁、读写锁、乐观锁等࿰…...
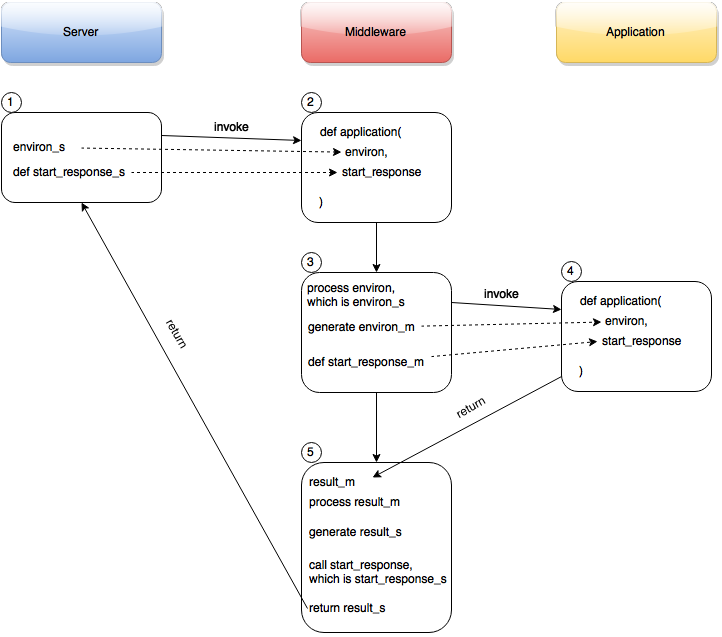
Python WSGI 与 Web 开发框架
目录 文章目录 目录WSGIWSGI 的工作原理environ 参数start_resposne 参数 WSGI 的中间件 WSGI Web 开发框架OpenStack 中的应用案例进程入口WSGI Application 加载Paste/PasteDeployRoutesWebOb WSGI Server 启动 WSGI WSGI(Web Server Gateway Interfaceÿ…...

[洛谷]P6464 [传智杯 #2 决赛] 传送门
看到数据范围:n<100,嗯......脑子闪过:还在想什么呢!Floyd啊。哈哈哈 思路: 详细注释: 话不多说,上ACcode!: #include<bits/stdc.h> using namespace std; #define int lo…...

Http协议和RestTemplate协议有什么区别?
目录 一、功能不同 二、技术不同 三、使用场景不同 四、总结 RestTemplate 是一个 Spring 框架提供的用于发送 HTTP请求的客户端工具,它封装了 Java 原生的 HTTP 客户端库,并提供了一组简洁易用的 API 来发送 HTTP 请求和处理响应。而 HTTPÿ…...
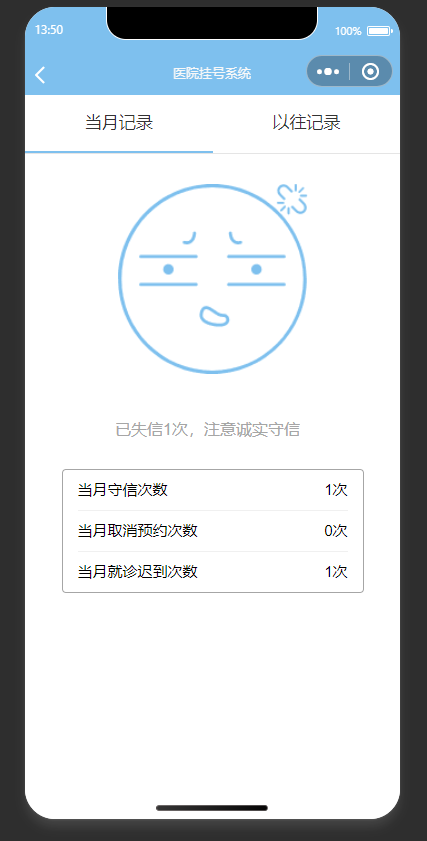
基于SpringBoot+微信小程序的医院预约叫号小程序
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 该项目是基于uniappWe…...

springboot整合RabbitMQ 消费端处理数据
pom 依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId></dependency>写一个rabbitmq配置文件 import org.springframework.amqp.core.Binding; import org.springframewo…...
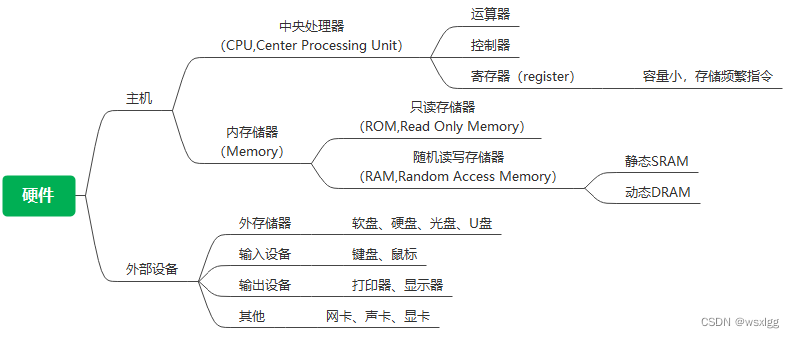
计算机中CPU、内存、缓存的关系
CPU(Central Processing Unit,中央处理器) 内存(Random Access Memory,随机存取存储器) 缓存(Cache) CPU、内存和缓存之间有着密切的关系,它们共同构成了计算机系统的核…...

【Linux实验】构造一个简单的 shell
一、实验目的 l 用 C/C++构造一个简单的 shell; l 理解 shell 程序的功能; l 学会 shell 的使用;...
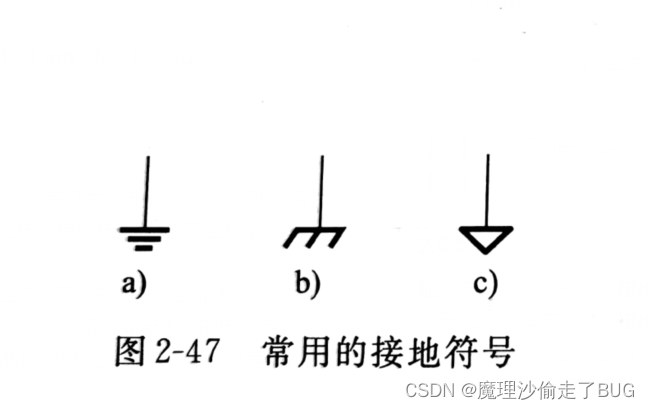
【电路原理学习笔记】第2章:电压、电流和电阻:2.6 电路
第2章:电压、电流和电阻 2.6 电路 2.6.1 电流的方向 电流方向有两种说法,一种按电子流动方向,另一种是传统的认为从正极流出到负极,这本教材采用传统电流方法。(事传统派,维新派输了,1&#…...

基于深度学习的人脸检测技术
用到环境 1、pycharm community edition 2022.3.2 2、Python 3.10 整篇内容都已上传至我的csdn资源中,想用的请移步。 流程 多任务级联卷积神经网络(Multi-task Cascaded Convolutional Networks, MTCNN)算法进行人脸检测 普通人脸检测 单人人脸检测 图1 单人人…...

【linux kernel】一文总结linux内核通知链
文章目录 1、通知链简介2、通知链的类型3、原理分析和API(1)注销通知器(2)注销通知器(3)通知链的通知 4、实例代码(1)定义一个通知链(2)实现观察者模块&#…...
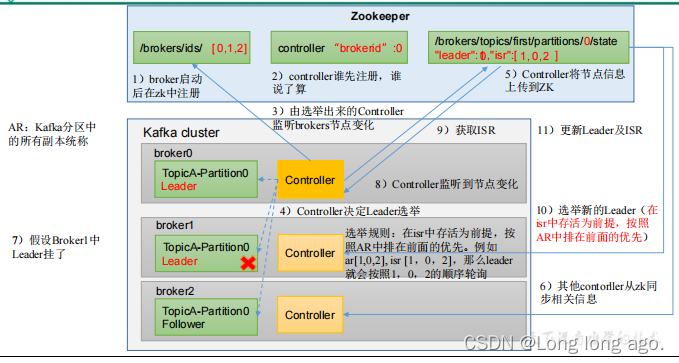
kafka入门,Kafka 副本(十三)
Kafka副本 副本基本信息 1)Kafka副本作用,提高数据可靠性 2)Kafka默认副本1个,生产环境一般配置2个,保证数据可靠性,太多副本会增加磁盘存储空间,增加网络上数据传输,降低效率 3&a…...
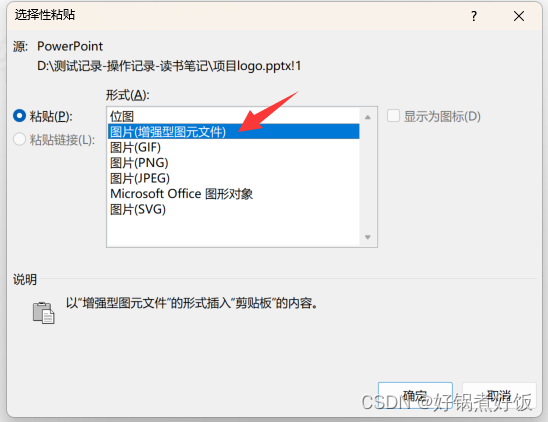
利用PPT制作简单的矢量图
1.用PPT画一个图形(可以多个图) 2.鼠标圈住图形 3.利用 Ctrl G 组合图形,再用 Ctrl C 复制 4.打开word—粘贴—选择性粘贴—图片(增强性图元文件) 确认即可。...

18-Linux 常用命令
目录 1.ls PS:FinalShell设置背景和字体 2.pwd 3.cd PS:认识 Linux 目录结构——Linux 是一个树形目录结构 PS:绝对路径 vs 相对路径 PS:使用 tab 键补全 PS:使用 ctrl c 重新输入 4.touch PS:L…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

Linux信号保存与处理机制详解
Linux信号的保存与处理涉及多个关键机制,以下是详细的总结: 1. 信号的保存 进程描述符(task_struct):每个进程的PCB中包含信号相关信息。 pending信号集:记录已到达但未处理的信号(未决信号&a…...
