前缀和模板算法
一)模板前缀和
【模板】前缀和_牛客题霸_牛客网 (nowcoder.com)
前缀和:快速的得出数组中某一段连续区间的和
暴力破解的话需要从头到尾的进行遍历,时间复杂度就可以达到O(N),而前缀和时间复杂度是可以达到O(1)的
第一步:预处理创建出一个前缀和数组dp,这个数组和原始数组规模是同等大小的
dp[i]就表示从[1,i]区间内所有数组的和
1到N区间内的和和1到L-1区间内的和本质上来说是同一类问题,研究问题的时候发现是同一类问题,我们就可以把这同一类问题抽象成状态表示,用动态规划的思想来进行解决
假设dp[3]表示的就是从1位置到3位置的所有元素的和,就是1+4+7=12
所以状态转移方程就是:dp[i]=dp[i-1]+array[i];
第二步:使用前缀和数组解决问题:
dp[i]=dp[r]-dp[l-1]
细节问题:在题干中下标为什么从1开始进行计数?
因为如果题目中给定的范围是0-2,那么势必会访问到dp[-1]此时dp表就会出现下标越界访问的情况
public class Main {public static void main(String[] args) { //1.输入数据Scanner scanner = new Scanner(System.in);int n=scanner.nextInt();int count=scanner.nextInt();long[] array=new long[n+1];for(int i=1;i<=n;i++){array[i]=scanner.nextLong();} //2.预处理一个前缀和数组long[] dp=new long[n+1];for(int i=1;i<=n;i++){dp[i]=array[i]+dp[i-1];} //3.使用前缀和数组while(count>0){count--;int left=scanner.nextInt();int right=scanner.nextInt();System.out.println(dp[right]-dp[left-1]);}} }二)二维前缀和
【模板】二维前缀和_牛客题霸_牛客网 (nowcoder.com)
一)预处理出来一个前缀和矩阵:这个前缀和矩阵必须和原始矩阵规模大小是一样的
dp[i][j]表示从(1,1)这个位置到(i,j)这段区间内,所围成的矩形的,这段区间内所有元素的和
dp[i][j]=dp[i-1][j]+array[i][j]+dp[i][j-1]-dp[i-1][j-1]
result=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]
自己画图可以不花正方形,可以直接画数进行分析
import java.util.Scanner; import java.util.Arrays; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public static void main(String[] args) { //1.先进行处理数据的输入Scanner scanner=new Scanner(System.in);int m=scanner.nextInt();int n=scanner.nextInt();int count=scanner.nextInt();//初始化输入次数long[][] array=new long[m+1][n+1];for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){array[i][j]=scanner.nextInt();}} //2.创建dp表进行填表,使用前缀和数组 long[][] dp=new long[m+1][n+1];for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+array[i][j]+dp[i][j-1]-dp[i-1][j-1];}} //2.进行返回结果,使用前缀和数组while(count>0){int x1=scanner.nextInt();int y1=scanner.nextInt();int x2=scanner.nextInt();int y2=scanner.nextInt(); long result=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]; // System.out.println(Arrays.deepToString(dp));System.out.println(result);count--; }} }
三)寻找数组的中心下标
724. 寻找数组的中心下标 - 力扣(Leetcode)
暴力枚举:每一次枚举一个中间下标i的时候,都需要把(0-i-1)之间的数进行相加,还需要把(i,array.length)之间的数进行相加一遍,可见时间复杂度会变得非常的高
一)定义一个状态表示:
f[i]表示从0号位置到i-1位置,所有元素的和
g[i]表示从i+1号位置到n-1位置,所有元素的和
二)根据状态表示推导状态转移方程
f[i]=f[i-1]+array[i-1]
g[i]=g[i+1]+array[i+1]
三)初始化(防止发生数组越界)
f[0]=0,g[n-1]=0
四)填表顺序:
f表:从左向右
g表:从右向左
class Solution {public int pivotIndex(int[] array) {int n=array.length;int[] f=new int[n];//f[i]表示从0号位置到i位置数组中这段区间内的和int[] g=new int[n];//g[i]表示从i+1号位置到n-1位置数组中这段区间的和//最后只是需要得出f[i]=g[i]即可f[0]=0;//填写到f[0]位置的时候数组就会发生越界g[n-1]=0;//因为填写到n-1位置的时候数组就会发生越界for(int i=1;i<n;i++){//f从前向后进行填表f[i]=f[i-1]+array[i-1];}for(int i=n-2;i>=0;i--){//g从后向前填表g[i]=g[i+1]+array[i+1];}for(int i=0;i<n;i++){if(f[i]==g[i]){return i;}}return -1;} }
四)除自身以外数组的乘积:
238. 除自身以外数组的乘积 - 力扣(Leetcode)
一)定义一个状态表示:
f[i]表示从0-i-1位置这段区间所有元素的乘积
g[i]表示从i+1位置开始到n-1这段区间内所有元素的乘积
二)根据状态表示推导状态转移方程:
f[i]=f[i-1]*array[i-1](0号位置的元素到i-2位置的元素的乘积再乘上array[i-1]位置的元素即可)
g[i]=g[i+1]*array[i+1](从i+2号位置的元素到n-1号位置的元素的乘积再乘以i+1号位置的元素)
三)进行初始化操作:f[0]=1,g[n-1]=1
四)填表顺序:f表从左向右填,g表从右向左填
class Solution {public int[] productExceptSelf(int[] array) { //1.创建前缀积以及后缀积数组int[] f=new int[array.length];int[] g=new int[array.length];int[] ret=new int[array.length];f[0]=1;g[array.length-1]=1; //2.初始化for(int i=1;i<array.length;i++){f[i]=f[i-1]*array[i-1];}for(int i=array.length-2;i>=0;i--){g[i]=g[i+1]*array[i+1];}for(int i=0;i<array.length;i++){ret[i]=f[i]*g[i];}return ret;} }
五)和为K的子数组
剑指 Offer II 010. 和为 k 的子数组 - 力扣(Leetcode)
是列出连续子数组
1)暴力解法:
1)采取枚举策略,定义两个变量i和j,i每次固定不动,j一直向后走,走一步加array[j],直到遇到sum和等于k,因为我们可以使用N^2的时间复杂度将所有子数组枚举出来
2)但是此时j应该继续向后走,直到j把整个数组遍历完成,因为有可能会出现j遇到整数又遇到负数的情况,此时应该还是让sum=sum+array[j],如果sum==k,应该再次让count++),此时的时间复杂度就是O(N^2),中心思路是找到以某一个位置为起点的子数组
不能使用双指针优化:必须有单调性
如果left到左箭头之间的和和right到右箭头之间的和是等于0的,因为right指针还是不断地向右进行移动,也就是说双指针会漏掉中间的这种情况
class Solution {public int subarraySum(int[] array, int k) {int count=0;for(int i=0;i<array.length;i++){int sum=0;for(int j=i;j<array.length;j++){sum=sum+array[j];if(sum==k) count++;}}return count;} }2)前缀和:快速的求出某一段区间的和
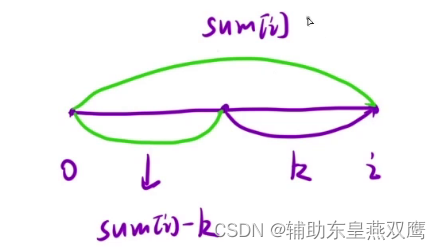
2.1)先找到以i位置为结尾的所有子数组(一定是包含i位置的元素的),先找到和为K的以i位置为结尾子数组有多少个,然后把所有情况都进行累加起来
2.2)从而就转化成了在[0~i-1]区间内,i前面有多少个前缀和等于sum[i]-k
2.3)找到所有以i为结尾的子数组中,有多少和是等于sum[i]-k的,就相当于是找到从0到i区间内的一个位置,使得[0,j-1]位置的和等于sum[i]-k,那么此时求的不就是前缀和dp[j-1]吗
1)如果真的采用上面的思路进行遍历查找[0-i]区间内有多少前缀和等于sum[i]-K,i下标需要从头到尾进行遍历一遍,每一次遍历i下标的时候,还需要从前缀和数组中从0-i位置进行遍历有看看有多少前缀和等于sum[i]-k的,此时就可以使用哈希表来进行记录0-i-1这段区间内的前缀和,这样绿线的部分直接就可以通过哈希表一次直接遍历出蓝色线的部分也就是直接可以求出有多少前缀和
2)那么最终的时间复杂度就是O(N^2)+K,时间复杂度又会飙升;
3)前缀和+哈希表
class Solution {public int subarraySum(int[] array, int k) {//dp[i]表示从0号位置到i号位置所有元素的和,开始初始化dp数组int[] dp=new int[array.length+1];dp[0]=0;for(int i=1;i<=array.length;i++){dp[i]=dp[i-1]+array[i-1];}System.out.println(Arrays.toString(dp));int count=0;//1.使用前缀和注意下标的映射关系 //2.注意新的dp数组left到right区间内的和有多少等于k是dp[right]-dp[left-1]是[left,right]区间内的和for(int left=1;left<=array.length;left++){for(int right=left;right<=array.length;right++){if(dp[right]-dp[left-1]==k) count++;}}return count;} }使用哈希表来进行解决,Hash<Int,Int>key存放的是前缀和,Value存放的是前缀和出现的次数,就不需要每一次从0位置到i-1位置来进行查找前缀和有多少等于sum-k的了,只需要统计前缀和出现的次数即可,如果发现sum[j]=sum[i]-k了,那么从j+1位置到i位置的这段区间内和就等于k
1)前缀和加入哈希表的时机:
第一种方式就是将前缀和全部计算出来,然后把前缀和一股脑地全部加入到哈希表中,然后从0号位置到i号位置一直进行遍历查找前缀和等于sum[i]-k的,这会出现重复的情况,可能会统计到i位置之后的前缀和等于sum[i]-k的值,可能会出现重复,但是我们是来查询i前面的前缀和等于sum[i]-k的;
再进行计算i位置之前,哈希表中只是保存[0,i-1]位置之间的前缀和
2)不用真的创建一个前缀和数组:
只需要使用sum来标记前一个位置的前缀和
3)如果整个前缀和等于K
当进行第一次枚举到i位置的时候,发现从0号位置到i位置数组的和是等于k的,那么此时就需要从[0,-1]区间内找一个前缀和等于0的位置,这显然是不存在的,所以应该提前加入到hash表中,hash<0,1>,就是为了避免这种情况被漏掉,所以先把(0,1)加入到哈希表中
class Solution {public int subarraySum(int[] nums, int k) {HashMap<Integer,Integer> result=new HashMap<>();result.put(0,1);int count=0;int sum=0;for(int i=0;i<nums.length;i++){sum=sum+nums[i];//记录当前位置的前缀和count=count+result.getOrDefault(sum-k,0);result.put(sum,result.getOrDefault(sum,0)+1);}return count;} }
六)和可被 K 整除的子数组
974. 和可被 K 整除的子数组 - 力扣(Leetcode)
1.暴力破解:找出所有前缀和(left到right区间可以被k整除的和,那么left到right区间内的和就可以被k整除)
class Solution {public int subarraysDivByK(int[] array, int k) {int n=array.length;int[] dp=new int[n+1];dp[0]=0;for(int i=1;i<=array.length;i++){dp[i]=dp[i-1]+array[i-1];}int count=0;for(int left=1;left<=array.length;left++){for(int right=left;right<=array.length;right++){int temp=dp[right]-dp[left-1];if(temp%k==0) count++;}}return count;} }2.暴力破解:找到所有的子数组,找出和能被k整除的
class Solution {public int subarraysDivByK(int[] array, int k) {int count=0;for(int i=0;i<array.length;i++){int sum=0;for(int j=i;j<array.length;j++){sum=sum+array[j];if(sum%k==0) count++;}}return count;} }3.前缀和:
1)同余定理:
1)sum[i]是从0号位置开始到i号位置开始所有元素的和,正好找到j位置使(sum[i]-x)%k==0
(sum[i]-x)/k=t.......0
2)所以说这个题就转化成了从0到i-1区间内,找到有多少个前缀和的余数等于sum%k
(sum%k+k)%k,(哪一个区间i前面的数的所有和%k=sum[i]%k)
3)创建一个哈希表:key是前缀和的余数,value是这个前缀和对应的出现的次数
lass Solution {public int subarraysDivByK(int[] array, int k) {HashMap<Integer,Integer> result=new HashMap<>();result.put(0,1);int count=0;int sum=0;for(int i=0;i<array.length;i++){sum=sum+array[i];count+=result.getOrDefault((sum%k+k)%k,0);result.put((sum%k+k)%k,result.getOrDefault((sum%k+k)%k,0)+1);}return count; } }
七)连续数组:
525. 连续数组 - 力扣(Leetcode)
算法原理:
1)将所有的0全部变成-1,然后求整个数组的和是0的最大子数组长度
2)在数组中找出最长的子数组,使子数组中所有元素的和等于0
细节问题:
1)哈希表中存什么?
hash<int,int>key值存放的是前缀和,value值存放的是前缀和所对应的下标
2)什么时候存入到哈希表?
使用完成之后丢入到哈希表
3)如果有重复的sum[i]怎么进行存放呢?
只是保留前面的那一对,i的值越靠近左边越好
4)默认有前缀和等于0的情况,如何进行处理?
hash[0]=-1
5)长度怎么算?
i-j+1-1=i-j
class Solution {public int findMaxLength(int[] array) {for(int i=0;i<array.length;i++){if(array[i]==0) array[i]=-1;}int count=0;int sum=0;HashMap<Integer,Integer> map=new HashMap<>(); //第一个位置存放的是前缀和,第二个位置存放的是下标,最终maxlen里面存放的是长度int maxlen=0;map.put(0,-1); //如果从0到i位置的元素和已经等于0了,那么此时就是在0到-1区间内寻找和是0的数组,此时长度就是i-0+1,所以要存放0,-1for(int i=0;i<array.length;i++){sum=sum+array[i];if(map.containsKey(sum)){maxlen=Math.max(maxlen,i-map.get(sum));}else{map.put(sum,i); //如果哈希表中已经存在sum了,就不需要再次进行存放了 //因为我们所需要进行寻找的是长度最大的数组} }return maxlen;} }
八)矩阵区域和
1314. 矩阵区域和 - 力扣(Leetcode)
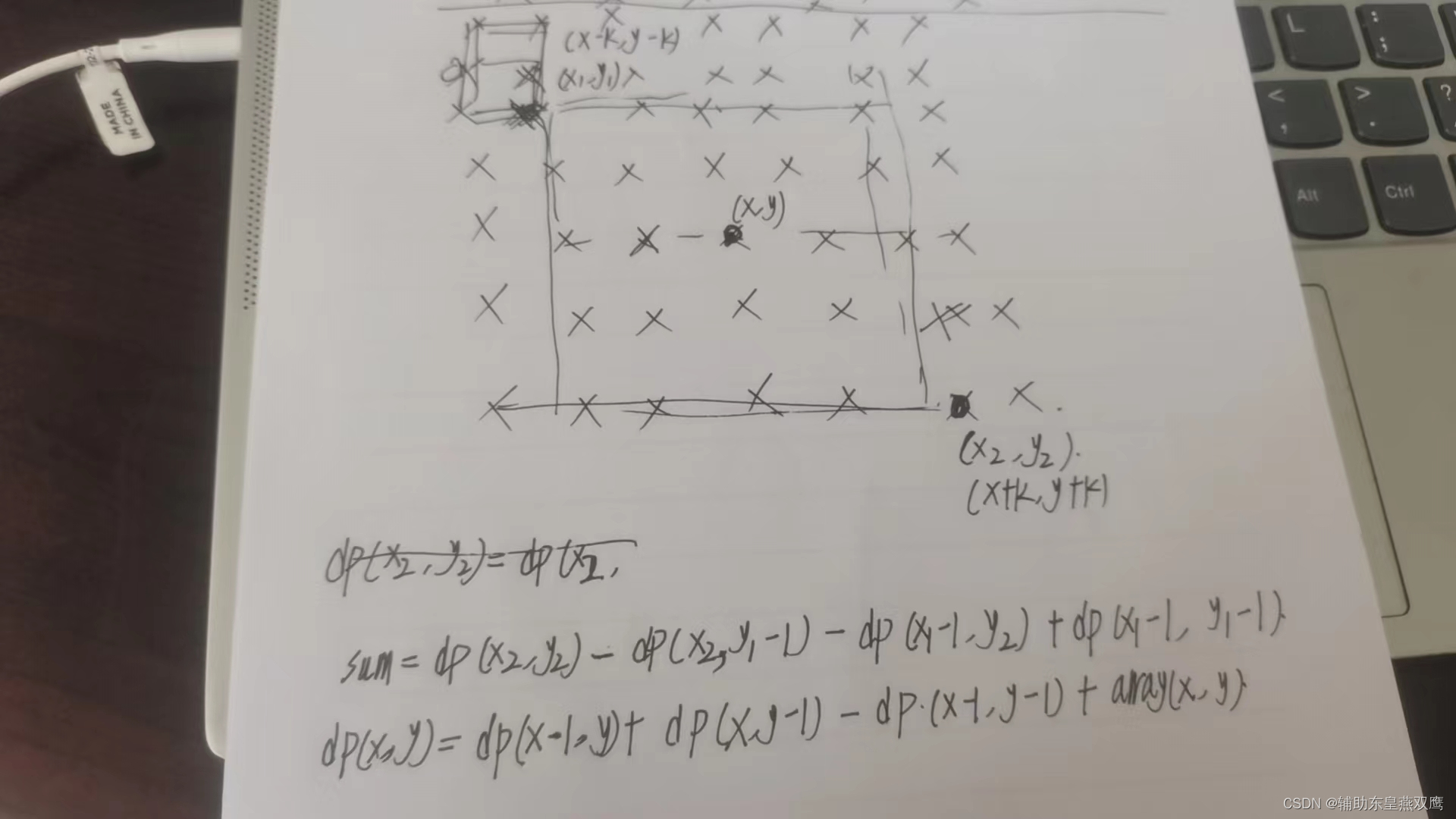
如下图所示,我们要求的中心下标的矩形面积是二维前缀和
(x+k,y+k)所围成的正方形的面积-(x-k,y-k)所围成的正方形的面积
class Solution {public int[][] matrixBlockSum(int[][] array, int k) {int col=array[0].length;int row=array.length;int[][] dp=new int[row+1][col+1];int[][] result=new int[row][col]; //1.初始化二维前缀和,注意下标的映射关系for(int i=1;i<=row;i++){for(int j=1;j<=col;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+array[i-1][j-1];}}System.out.println(Arrays.deepToString(dp)); //2.计算最终矩阵的值,注意下标的映射关系for(int i=0;i<row;i++){for(int j=0;j<col;j++){int x1=Math.max(i-k,0)+1;int y1=Math.max(j-k,0)+1;int x2=Math.min(i+k,row-1)+1;int y2=Math.min(j+k,col-1)+1;result[i][j]=dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1];}}return result;} }
相关文章:
前缀和模板算法
一)模板前缀和 【模板】前缀和_牛客题霸_牛客网 (nowcoder.com) 前缀和:快速的得出数组中某一段连续区间的和 暴力破解的话需要从头到尾的进行遍历,时间复杂度就可以达到O(N),而前缀和时间复杂度是可以达到O(1)的 第一步:预处理创建出一个前缀和数组dp&a…...
)
SpringBoot 启动输出 Git 版本信息(2023/07/11)
SpringBoot 启动输出 Git 版本信息 文章目录 SpringBoot 启动输出 Git 版本信息1. 环境依赖2. pom.xml 配置3. 启动类配置 为了方便记录项目打包时的 Git 版本,本文将介绍如何将 Git 版本信息打包进 JAR 文件,并在项目启动时输出。 1. 环境依赖 SpringB…...

SSH客户端连接远程服务器
目录 一、什么是客户端连接远程服务器 二、什么是服务端连接远程服务器 三、查看网络信息 1、图形程序查看网络信息 2、命令查看网络信息 四、SSH客户端(Linux) 五、SSH客户端(windows) 六、SSH远程服务器 一、什么是客户…...

“深入理解Redis:高性能缓存与数据存储的秘密“
标题:深入理解Redis:高性能缓存与数据存储的秘密 在现代应用程序的开发中,缓存和数据存储是非常重要的组成部分。它们不仅可以提高应用程序的性能,还可以减轻数据库和网络的负载。其中,Redis作为一种高性能的内存数据存…...
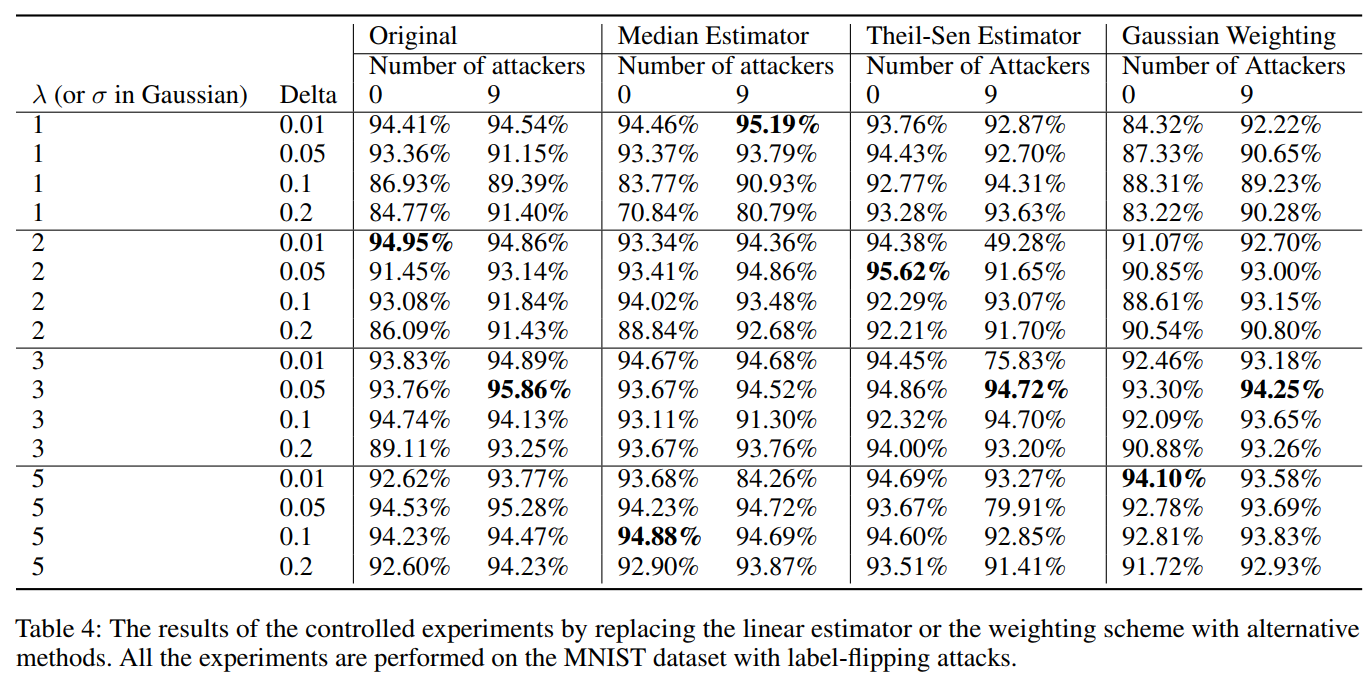
【论文阅读笔记】Attack-Resistant Federated Learning with Residual-based Reweighting
个人阅读笔记,如有错误欢迎指出 Arxiv 2019 [1912.11464] Attack-Resistant Federated Learning with Residual-based Reweighting (arxiv.org) 问题: 联邦学习容易受到后门攻击 创新: 提出一种基于残差的重新加权聚合算法 聚合算法…...
DevOps B站学习版(二)
学习地址: 01.DevOps的诞生_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Pt4y1H7Zq/?p1&vd_source1f09c23f556b3d6a9b7706f8db12fa54%E3%80%81 正文开始 找到这个地方,修改 可以写成基于标签拉取和构建工程,下面也选择Tag即可…...

MySQL(一)基本架构、SQL语句操作、试图
MySQL系列文章 MySQL(一)基本架构、SQL语句操作、试图 MySQL(二)索引原理以及优化 MySQL(三)SQL优化、Buffer pool、Change buffer MySQL(四)事务原理及分析 MySQL(五&a…...

MySQL事务基础知识
文章目录 一、事务简介二、事务操作1.查看事务提交方式2.设置事务提交方式3.开启事务4.提交事务5.回滚事务 三、事务四大特性ACID四、并发事务的问题五、并发事务隔离级别六、代码实例1.脏读实例2.不可重复读实例3.幻读的实例4.串行化的实现 一、事务简介 事务是一组操作的集合…...
form表单禁止浏览器自动填充密码
因为用户修改密码的时候,谷歌浏览器、edge等浏览器,总是自动将保存的密码填充到重置密码输入框中,给用户使用带来困扰。原因是因为你在登录的时候选择记住了账号和密码了,所以就会把信息存在浏览器里面,当你在修改密码的时候,由于form表单的 type="password" 所…...
ios oc button 设置
Button调整内部的子控件的位置...
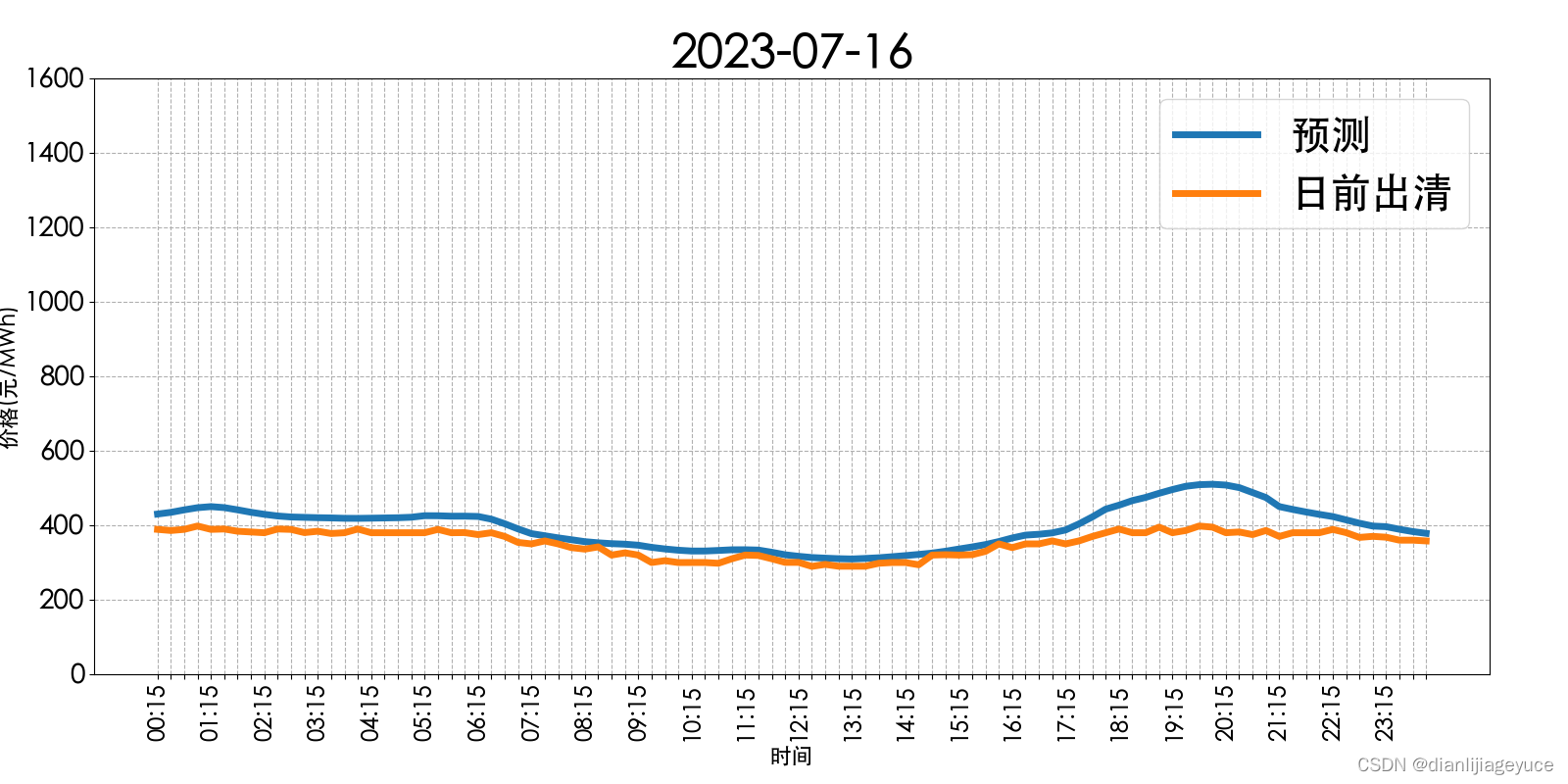
山西电力市场日前价格预测【2023-07-17】
日前价格预测 预测明日(2023-07-17)山西电力市场全天平均日前电价为335.50元/MWh。其中,最高日前电价为377.51元/MWh,预计出现在06: 00。最低日前电价为271.94元/MWh,预计出现在13: 30。 价差方向预测 1:实…...
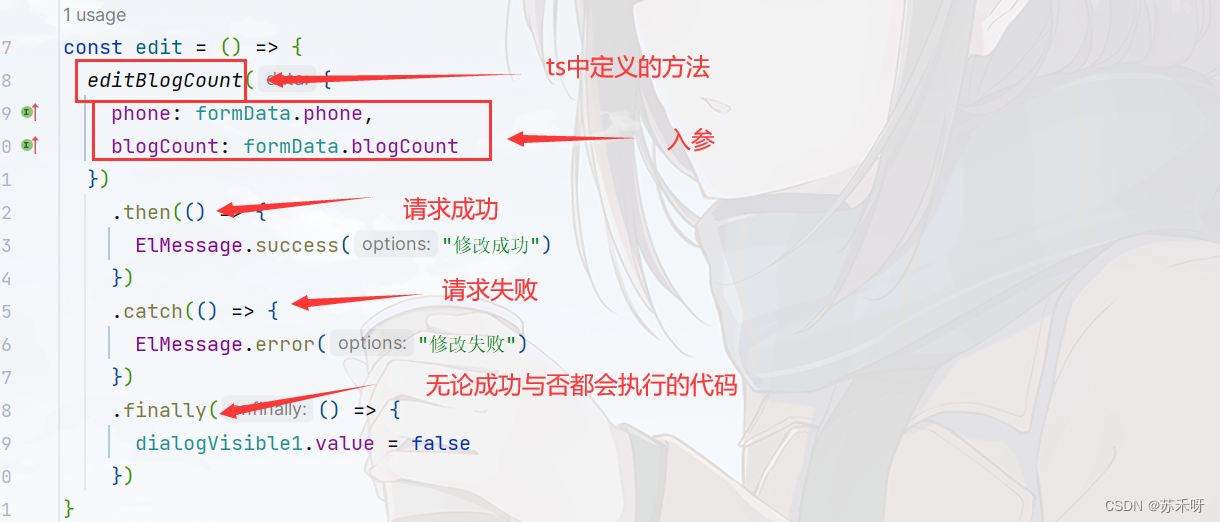
vue3功能实现
在vue2中,要实现一些方法(增删改查)一般都是写在一起的。如下图所示: 但是在vue3中,实现一个方法需要用到很多文件。 方法定义方法如下: export function classSign(phone: string) {return sign_reques…...

微服务系列文章 之 SpringCloud中遇到的一些bug
1、There was a problem with the instance info replicator 错误原因: 该服务尝试将自己作为客服端注册解决办法: 在application.yml配置文件中,设置 # 注册Eureka服务 eureka:client:# Eureka服务注册中心会将自己作为客户端来尝试注册它自…...
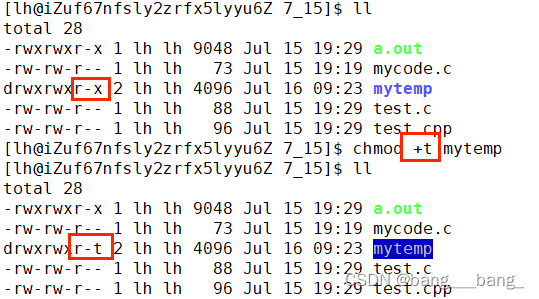
Linux——权限
目录 1.Shell运行原理——外壳程序 2.权限 2.1对人操作 2.2对角色和文件操作 3.常见权限问题 1.Shell运行原理——外壳程序 首先我们要明确一个概念,我们不是直接访问操作系统。为什么? 对于Windows我们是使用GUI进行操作,Shell对于Li…...

[英语单词] components;
*[kәm’pәunәnt] n. 元件, 组件, 成分 a. 组成的, 构成的 【计】 组件 【化】 组分 【医】 成分; 组元(神经元组) 有很多地方使用这个单词,在组成整体时,作为单位一内的占有比率。那为什么不用portion? 这样每一个组成部分都是一个compon…...

【观察者模式】 ——每天一点小知识
💧 观察者模式 \color{#FF1493}{观察者模式} 观察者模式💧 🌷 仰望天空,妳我亦是行人.✨ 🦄 个人主页——微风撞见云的博客🎐 🐳 《数据结构与算法》专栏的文章图文并茂🦕…...

el-ment ui 表格组件table实现列的动态插入功能
在实际需求中我们经常遇到各种奇葩的需求,不足为奇。每个项目的需求各不相同,实现功能的思路大致是一样的。 本文来具体介绍怎么实现table表格动态插入几列。 首先实现思路有2种, 1. 插入的位置如果是已知的,我知道在哪个标题的…...

gitLab修改密码后,sourceTree如何修改密码
修改gitLab密码后,在sourceTree提交或者更新代码会报:fatal: Authentication failed for~ 简单粗暴的方法: 到C:\Users\用户\AppData\Local\Atlassian\SourceTree,找到passwd文件,并删除; 重启sourceTre…...

sop是什么意思
标准作业程序 执行复杂的日常事务所设计的内部程序 内容 所谓SOP,是 Standard Operating Procedure三个单词中首字母的大写 ,即标准作业程序,指将某一事件的标准操作步骤和要求以统一的格式描述出来,用于指导和规范日常的工作。…...
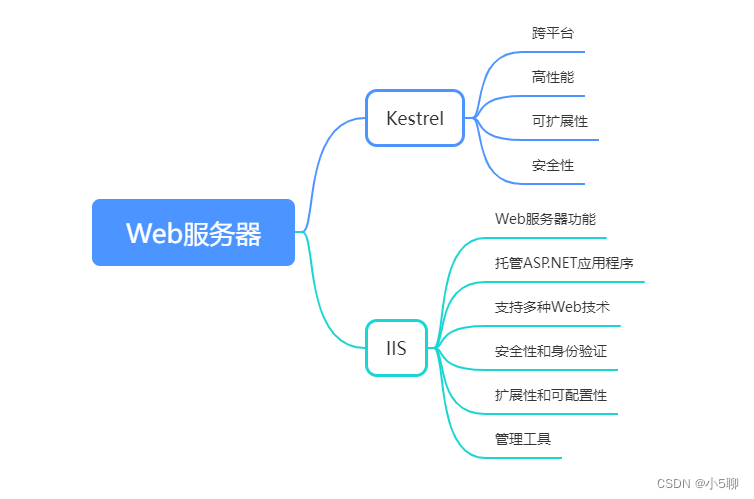
【C#】Kestrel和IIS服务器下的同步与异步配置
最近在回看自己写的代码时,发现服务配置里最开头写了两段代码,第一感觉,这是啥功能,太久有点生疏了,经过一顿搜索和回顾,简单整理如下 目录 1、Kestrel服务器1.1、跨平台1.2、高性能1.3、可扩展性1.4、安全…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...