金三银四丨黑蛋老师带你剖析-CTF岗
作者丨黑蛋
二进制是个庞大的方向,对应着许许多多方向的岗位,除了之前说过的逆向岗位,漏洞岗位,病毒岗位,还有专门打CTF的岗位,CTF是网络安全领域的一种比赛。普遍来讲,大学生学习网络安全都会参加CTF相关比赛,而有相应含金量证书,也是对找工作很有帮助的。首先我们来看一看CTF是什么:
CTF是一种流行的信息安全竞赛形式,其英文名可直译为“夺得Flag”,也可意译为“夺旗赛”。其大致流程是,参赛团队之间通过进行攻防对抗、程序分析等形式,率先从主办方给出的比赛环境中得到一串具有一定格式的字符串或其他内容,并将其提交给主办方,从而夺得分数。为了方便称呼,我们把这样的内容称之为“Flag”。
而CTF竞赛方式分为俩种,一种是解题模式,主办方给出各种方向的题目,交由参赛选手进行寻找Flag,比较常规的就是一个界面,输入正确的Flag就可以通过,然后选手分别施展手段,在主办方给出网站啊,服务器啊,软件,文件等各种乱七八糟的内容中寻找Flag;而另一种就是攻防模式,又叫AWD,每队管理一个或多个服务器,然后相互攻击和防守,挖掘漏洞并攻击对手来获得分数,是比较激烈的一种比赛模式。最后根据获取的分数进行排名。下面来简单看一下CTF中解题模式中的各个方向侧重点:
1.CHOICE:选择题包含关于信息安全的各类知识点,难度系数偏低,适合刚接触信息安全的人士来全面的了解安全行业的情况
2.BASIC: 主要考察基础的计算机与网络安全知识,涉及信息发掘、搜索、嗅探、无线安全、正则表达式、SQL、脚本语言、汇编、C语言以及简单的破解、溢出等知识。旨在普及信息安全知识,引领信息安全爱好者入门
3.WEB: 考察脚本注入、欺骗和跨站等脚本攻击技术
4.REVERSE: 考察逆向破解的相关技术,要求有较高的汇编语言读写能力,以及对操作系统原理的认识
5.PWN: 考察软件漏洞挖掘、分析及利用技术,探索二进制代码背后的秘密,要求对漏洞有一定理解,掌握操作系统原理的相关知识(自我感觉最有难度的)
6.MOBILE: 考察移动终端安全相关知识
7.MISC: 即杂项,考察各种计算机系统与网络安全知识,涉及隐写术、流量分析、内核安全等信息安全的各个领域。
8.PPC:即编程类题目,题目涉及到编程算法
9.CRYPTO:即密码学,题目考察各种加解密技术,包括古典加密技术、现代加密技术甚至出题者自创加密技术。
当然并不是每次比赛主办方都会给出各种方向的题目让大家做,比较主流的事PWN,MISC,REVERSE。这里REVERSE和PWN属于二进制方向,也是我们方向找工作,会在CTF中负责的模块,要么负责出题,要么负责打比赛,REVERSE就是逆向,它比较杂乱,不仅仅有Windows平台上的题目,还会给安卓平台上的题目,还有各种语言写成的文件,Java、go、python、C、C++等,然后又会有各种壳,VM,反调试手段,各种加密算法的考验,REVERSE一直以来都是CTF比赛中难度最大的一个方向。而PWN大部分是考验Linux平台,属于漏洞相关的知识,一般来讲CTF相关的安服岗位,REVERSE和PWN并不分家。接下来我们找一找CTF相关的岗位:
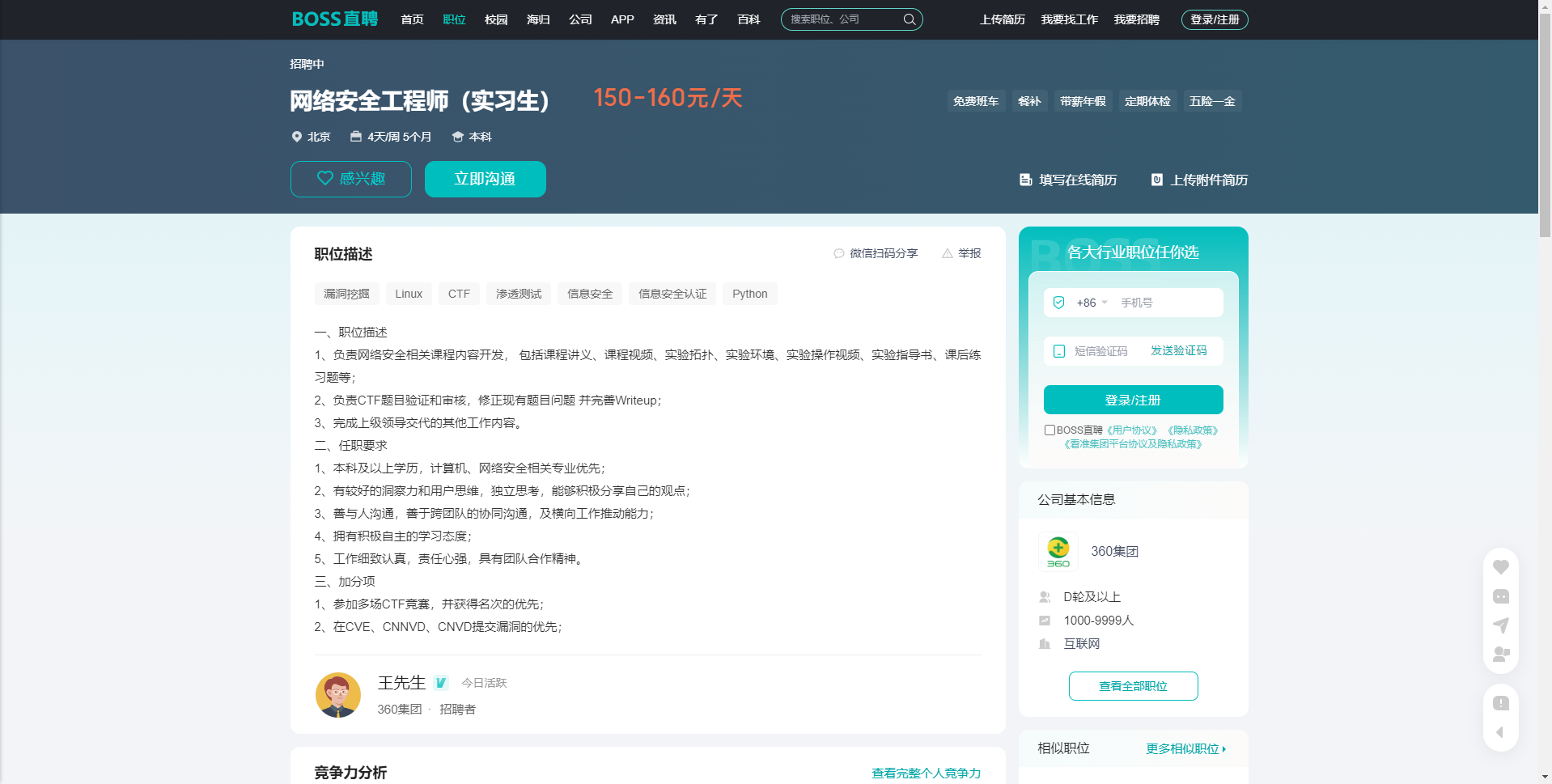

像这个岗位就是负责CTF比赛中的出题审核环节,然后完善Writeup,Writeup就是每次比赛完,官方亦或者各种做出来题目的参赛选手给出的解题思路,当然随时组队参赛也是默认工作范畴。
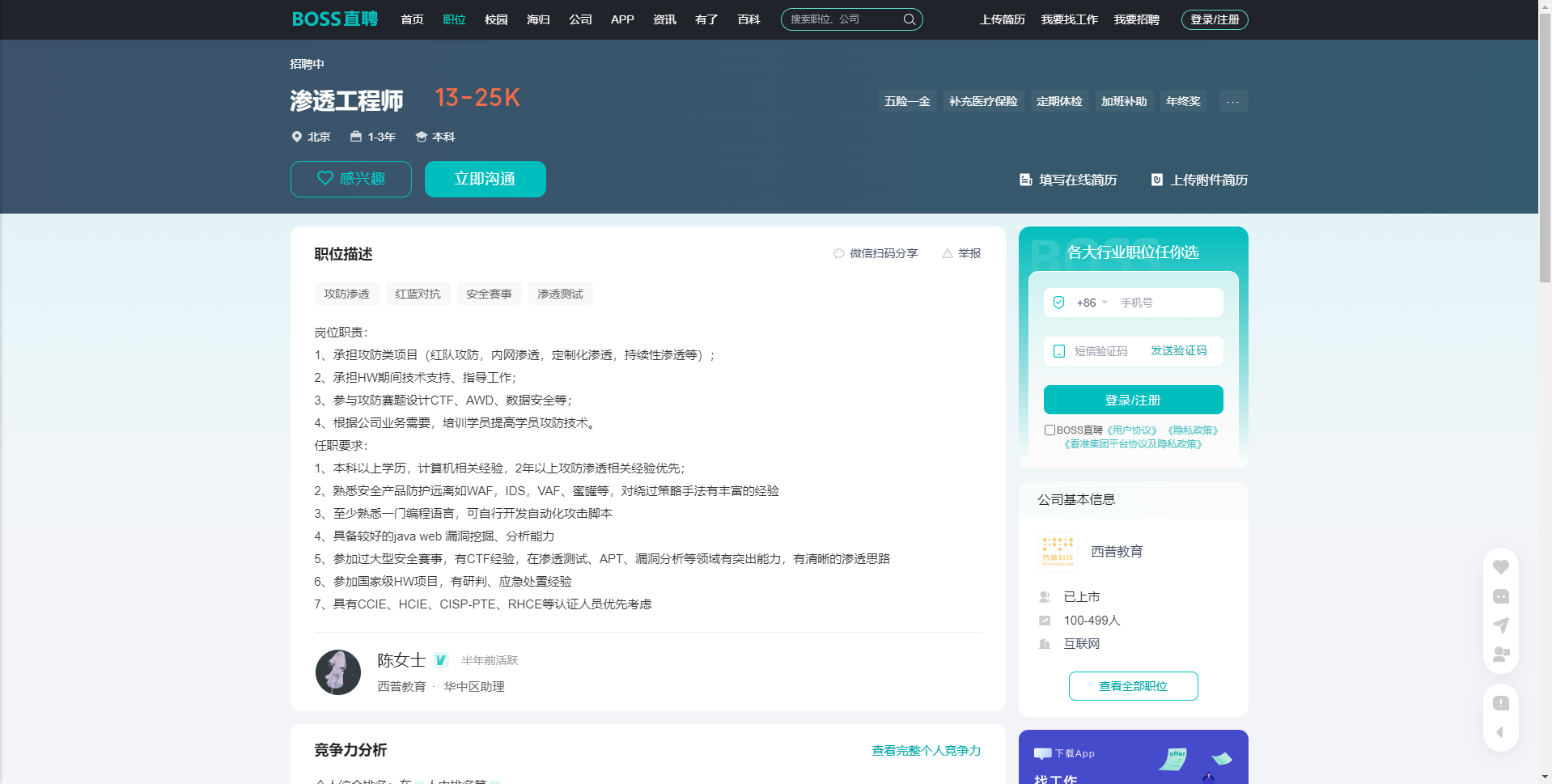
这个要求比较多,和CTF相关,设计CTF,AWD的题目设计,以及对学员进行培训等。
而CTF的基础知识就很杂了,不单单属于二进制范畴,但是REVERSE和PWN是属于二进制方向的,基础知识也都是差不多,而REVERSE涉及的平台更多,PWN主要是在Linux平台。
相关文章:
金三银四丨黑蛋老师带你剖析-CTF岗
作者丨黑蛋二进制是个庞大的方向,对应着许许多多方向的岗位,除了之前说过的逆向岗位,漏洞岗位,病毒岗位,还有专门打CTF的岗位,CTF是网络安全领域的一种比赛。普遍来讲,大学生学习网络安全都会参…...
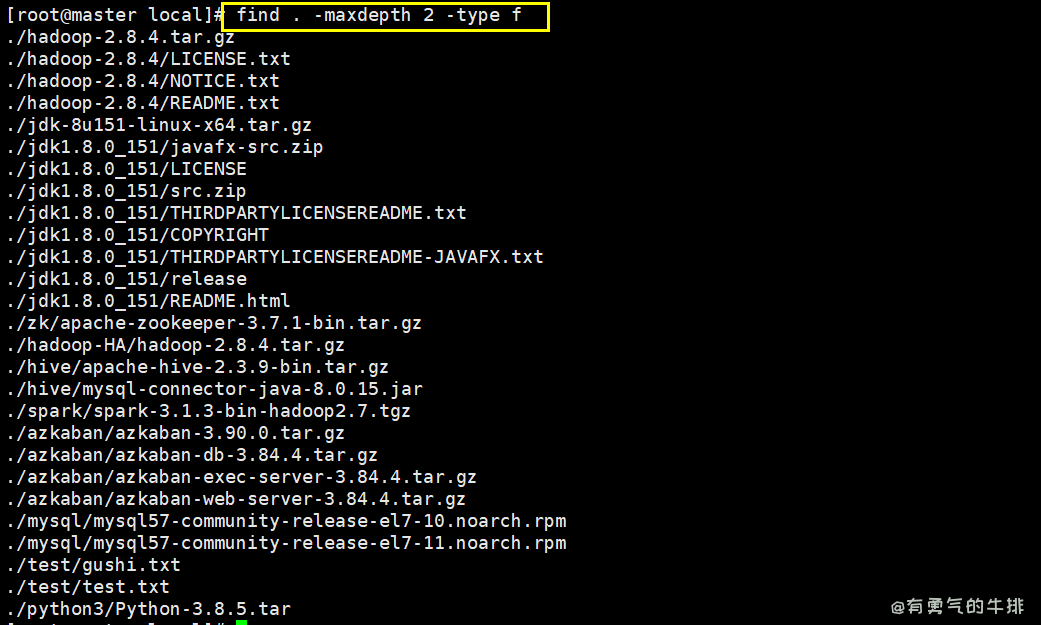
Linux find命令
哈喽,大家好,我是有勇气的牛排(全网同名)🐮 有问题的小伙伴欢迎在文末评论,点赞、收藏是对我最大的支持!!!。 1 介绍 find命令用来查找置顶目录下的文件。任何位于参数…...
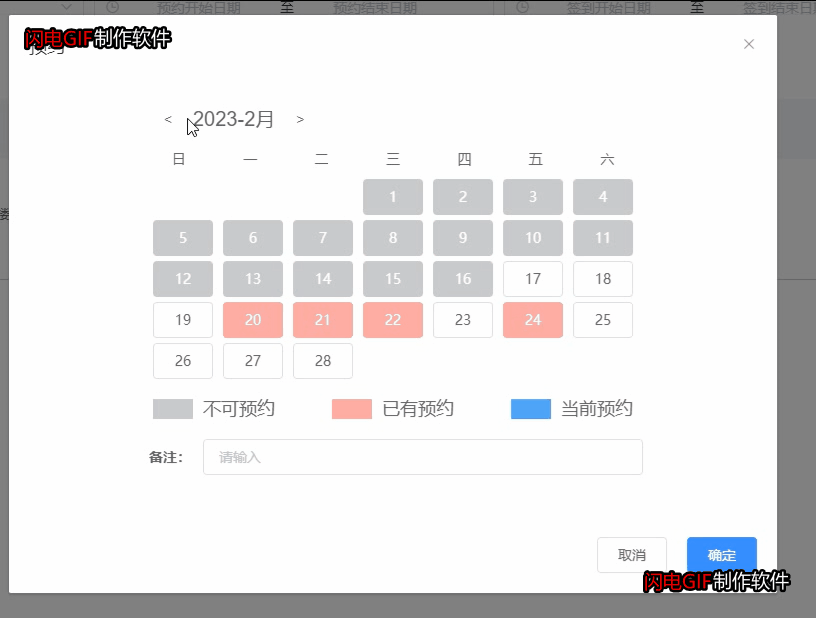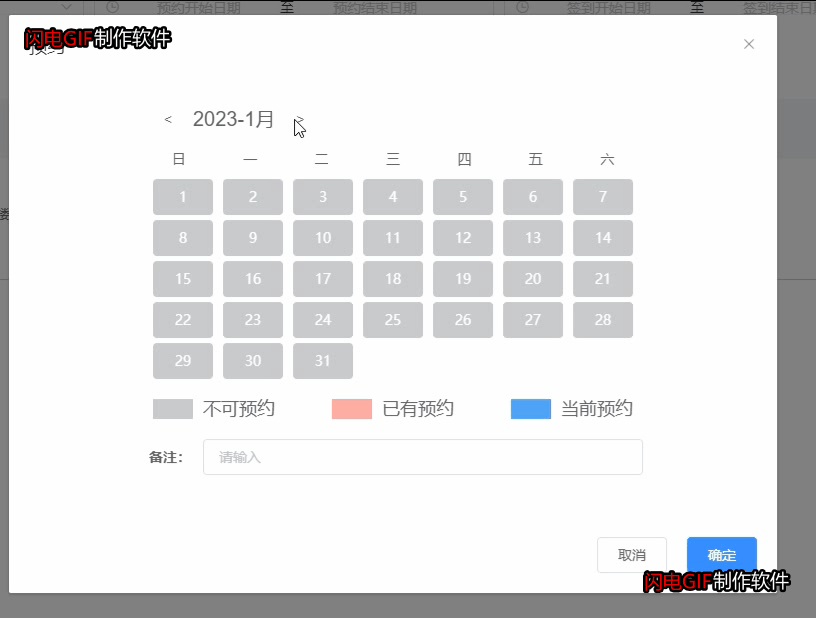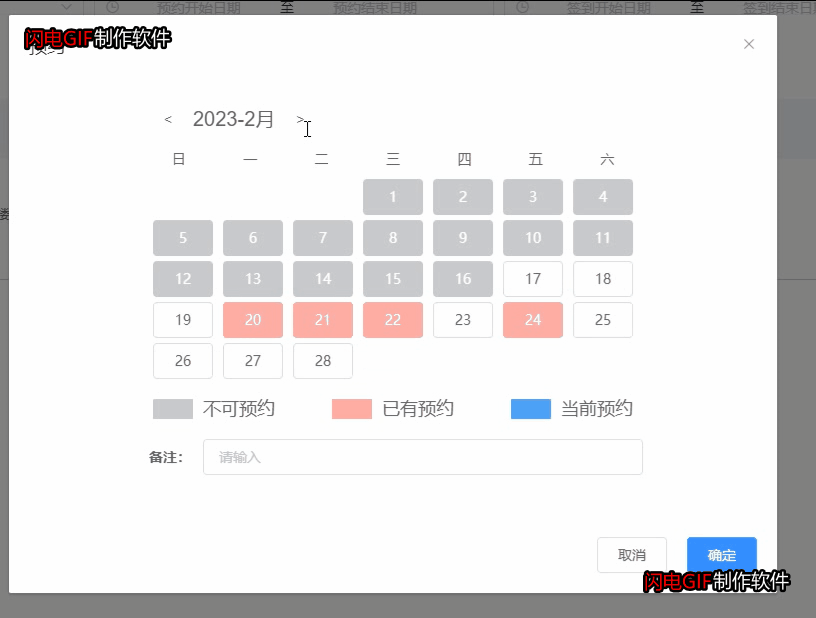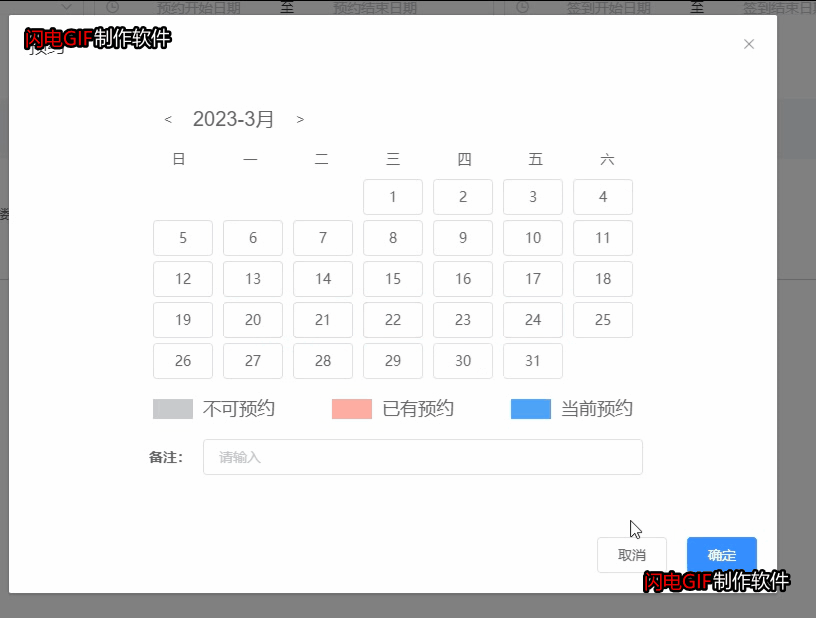
vue项目实现会议预约(包含某天的某个时间段和某月的某几天)
一、一天的时间段预约 会议预约有以下操作: 1.点击预约按钮,弹窗最近一周的预约时间点(半小时一个点),预约时间为5:00到24:00; 2.超过当前时间的时间点不允许再预约,已经预约的时间不允许再预约,…...

javacv桌面推送 通过推送和拉取udp组播视频流实现
ffmpeg udp 推流拉流命令单播推流E:/工具/ffmpeg/ffmpeg -f gdigrab -r 23 -i desktop -pkt_size 1316 -vcodec libx264 -preset:v ultrafast -tune:v zerolatency -f h264 udp://192.168.1.20:5001拉流ffplay -f h264 udp://192.168.1.20:5001 -fflags nobuffer -nofind_strea…...
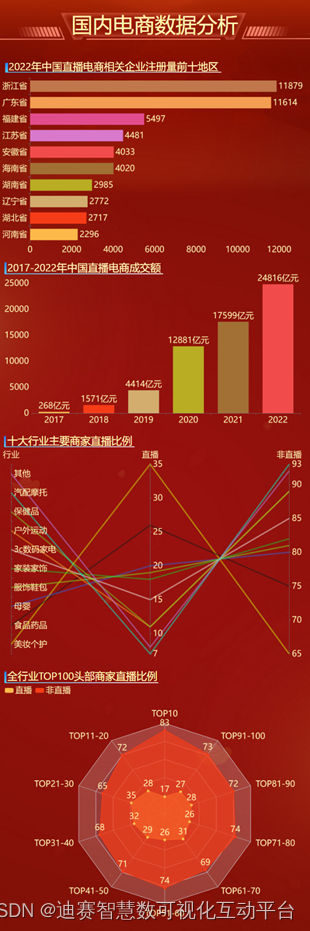
2022年直播电商成交额,更是达到了24816亿元的成交额
近年来移动网络覆盖率、网速提升,直播行业不在是陌生的行业,直播也诞生了繁多的领域,游戏直播、户外直播等,当然还有今天的主题“直播带货”。直播带货是线上销售模式的一种,由衷是为了更好的把商品展示给用户观看&…...

【学习总结】2023寒假总结
写在前面时光匆匆,白驹过隙,转眼间寒假就过去了,这次寒假可以算的上是最长的一次假期,经历了从疫情到放开,从患病到阳康,在现实与虚幻的世界中玩耍,在痛苦的数据结构中徘徊,在每次早…...
宝塔搭建实战php源码人才求职管理系统后台端thinkphp源码(一)
大家好啊,我是测评君,欢迎来到web测评。 在开源社区里看到了这一套系统,骑士人才系统SE版,搭建测试了,感觉很不错。能够帮助一些想做招聘平台的朋友降低开发成本,就是要注意,想商业使用的话&…...
stk 根据六根数文件生成卫星轨迹(一)
先简单介绍下上面的参数。 Propagator预报轨道模型。 TwoBody为二体(开普勒运动模型)。HPOP为高精度轨道模型。目前只用到这两个。 下图为六根数参数 Orbit Epoch:为根数时间(UTC) Semimajor Axis:长半…...
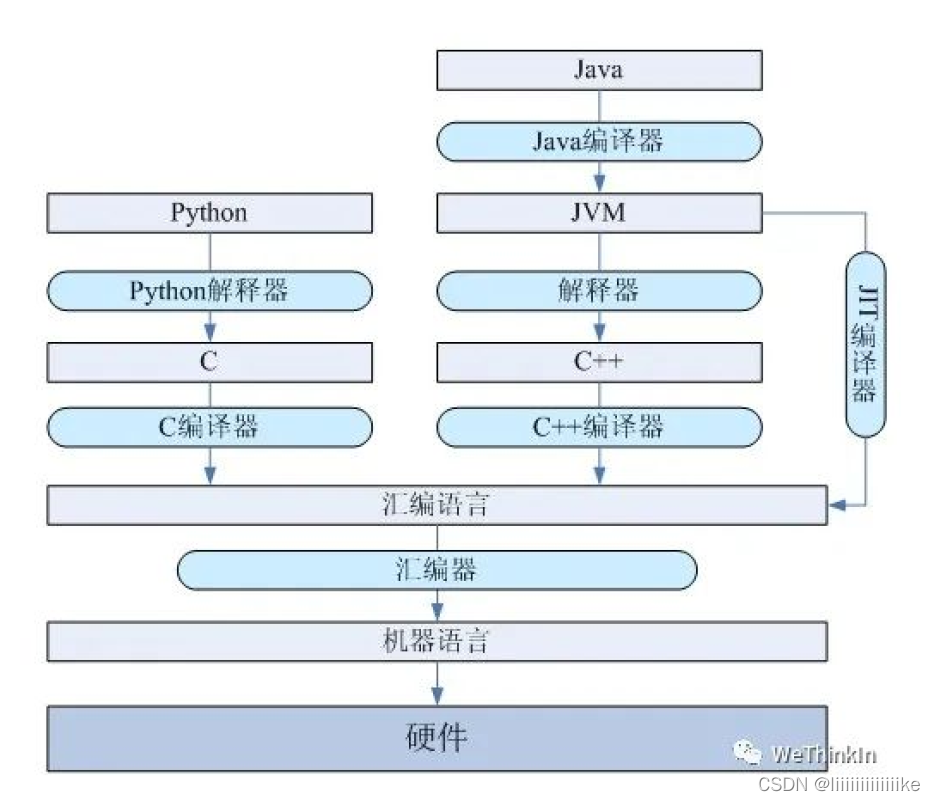
深度学习算法面试常问问题(一)
博主秋招遇到的面试问题以及整理其他面经相关问题,无偿分享~ 项目叙述: 算法需求及应用场景算法的调研和初步方案的制定数据的准备(包括数据标注和数据增强)算法的介绍(包括输入和输出,loss、backbone、训…...
Spring 底层原理与解析 - 容器接口
Spring 底层原理与解析 - 容器接口 BeanFactory 能做哪些事 BeanFactory 与 ApplicaiotnContext 到底是谁提前做完了对象的加载 在之前的一篇关于 Spring 的文章Spring IoC 与容器的初始化中提到过,BeanFactory 接口与 ApplicationContext 接口之间的关系 可以看…...
Compose-Navigation简单案例上手
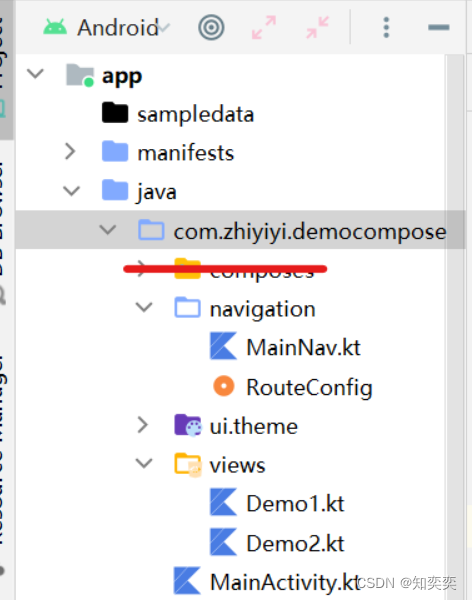
Navigation 快速上手 下面案例简要展示使用 Compose 版本的 Navigation 库来实现两个页面之间的跳转 这是完整的结构(忽略掉红线划过的那个包) 安装适用于 kotlin 的 navigation 依赖 dependencies {implementation("androidx.navigation:navigati…...

855. 考场就座
题目 考场就座 在考场里,一排有 N 个座位,分别编号为 0, 1, 2, …, N-1 。 当学生进入考场后,他必须坐在能够使他与离他最近的人之间的距离达到最大化的座位上。如果有多个这样的座位,他会坐在编号最小的座位上。(另外…...
)
k8s之ingress(二)
文章目录k8s之ingress1.1、Kubernetes 暴露服务的方式:1.2 基本概念1.3为什么需要Ingress资源1.4 Ingress的工作原理1.5ingress 暴露服务的方式总结k8s之ingress 1.1、Kubernetes 暴露服务的方式: Kubernetes暴露服务的方式目前只有三种:LoadBlancer Service、Nod…...
linux下监测串口数据
在编写上下位机通信代码时,需要分阶段测试,确保下位机,线路,上位机都OK. 一.检查设备数据传出 1.确定下位机的串口参数 如果波特率有问题,可能会…...
三分钟深入理解闭包(附详解实例))
【面试之闭包】前端面试那些事(2)三分钟深入理解闭包(附详解实例)
目录1、什么是闭包,什么是作用域1.1 变量作用域1.2 闭包是啥?如何改变变量调用格局1.3 闭包的特性2、怎么用闭包,闭包实例应用2.1 常见闭包实例2.2 闭包异步函数的应用2.3 柯里化的应用3、闭包的优缺点3.1 优点3.2 缺点4、片尾彩蛋【写在前面…...

深入浅出带你学习WebSphere中间件漏洞
前言 上一篇文章给大家介绍了中间件glassfish的一些常见漏洞以及利用方法,今天我给大家带来的是WebSphere中间件的常见漏洞以及这些漏洞的利用方法,下面我们首先介绍一下WebSphere中间件是什么,然后展开来讲关于该中间件的漏洞。 WebSphere…...

如何一眼分辨是C还是C++
C语言的历史C语言是由贝尔实验室的Dennis Ritchie在20世纪70年代初开发的一种通用程序设计语言。在早期的计算机时代,许多计算机使用不同的汇编语言编写程序,这导致了程序的可移植性和代码的可重用性很低。因此,Dennis Ritchie在开发C语言时试…...
CMake系列:正确使用多配置编译系统
目录 常见错误 问题现象 正确做法 if指令应该什么时候使用 活学活用 把IF指令用于多配置编译系统是很多初学者容易犯下的错误。这篇文章启示性的教你如何正确理解、使用CMake的多配置编译系统。 常见错误 以Debug和Release配置有不同的宏定义为例,如下所示&a…...
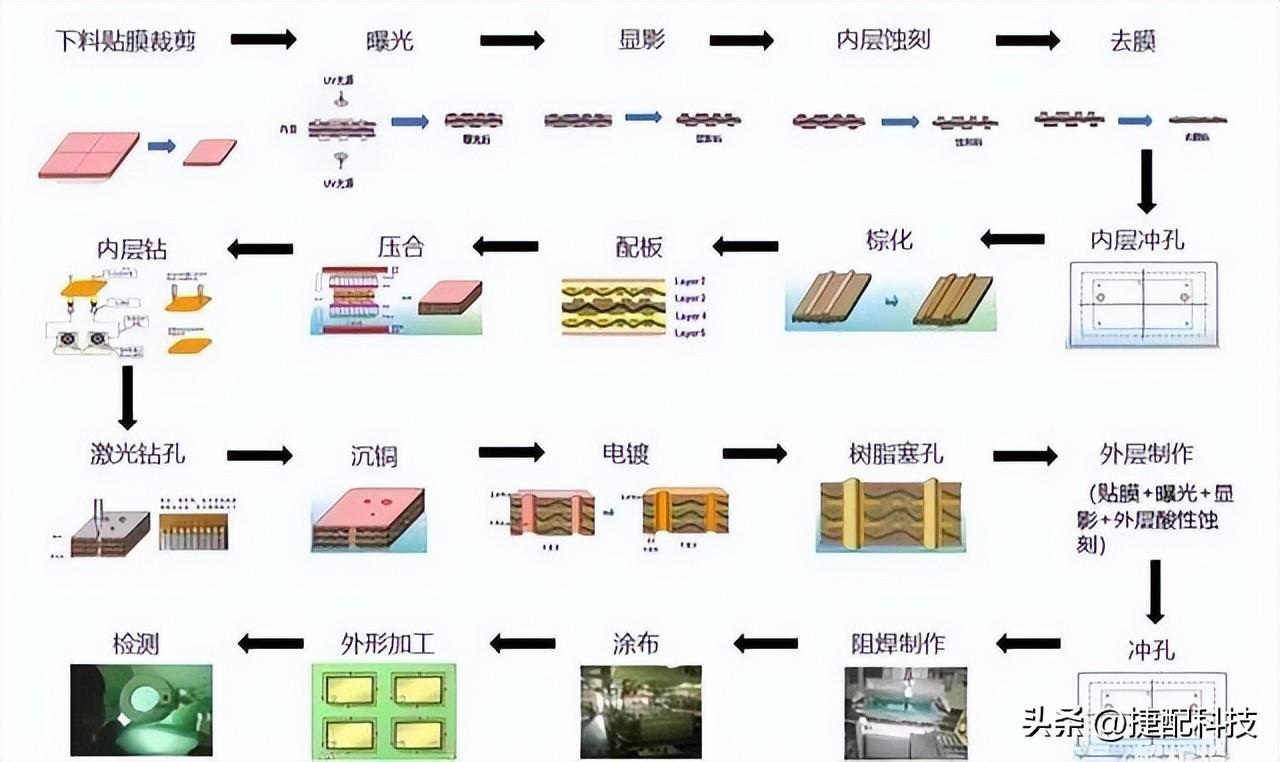
PCB中的HDI板生产中的变化
关键词:HDI概述 HDI发展演变 HDI生产难点如果把一整个电子产业比作浩瀚的宇宙,那些智能电子设备就像宇宙中闪耀的星光,当你以“上帝”的视角手持放大镜去观察时,这些闪烁的星光点点其实都是一个个由精密的“自然规律”所“设计”好…...

程序分析与神经网络后门
原文来自微信公众号“编程语言Lab”:程序分析与神经网络后门 搜索关注“编程语言Lab”公众号(HW-PLLab)获取更多技术内容! 欢迎加入编程语言社区 SIG-程序分析,了解更多程序分析相关的技术内容。 加入方式:…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
