Normalization(BN and LN) in NN

Batch Normalization
称为批标准化。批是指一批数据,通常为 mini-batch;标准化是处理后的数据服从 N ( 0 , 1 ) N(0,1) N(0,1) 的正态分布。在训练过程中,数据需要经过多层的网络,如果数据在前向传播的过程中,尺度发生了变化,可能会导致梯度爆炸或者梯度消失,从而导致模型难以收敛。
假设输入的 mini-batch 数据是 B = x 1 . . . x m B={x_1...x_m} B=x1...xm,Batch Normalization 的可学习参数是 γ , β \gamma, \beta γ,β,步骤如下:
- 求 mini-batch 的均值: μ B ← 1 m ∑ i = 1 m x i \mu_B\gets \frac{1}{m} {\textstyle \sum_{i=1}^{m}}x_i μB←m1∑i=1mxi
- 求 mini-batch 的方差: σ B 2 ← 1 m ∑ i = 1 m ( x i − μ B ) \sigma_B^2\gets \frac{1}{m} {\textstyle \sum_{i=1}^{m}}(x_i-\mu _B) σB2←m1∑i=1m(xi−μB)
- 标准化: x i ^ ← x i − μ B σ B 2 + ϵ \widehat{x_i} \gets \frac{x_i-\mu_B}{\sqrt{\sigma_B^2+\epsilon } } xi ←σB2+ϵxi−μB,其中 ϵ \epsilon ϵ 是防止分母为 0 的一个数。
- affine transform(缩放和平移): y i ← γ x i ^ + β ≡ B N r , β ( x i ) y_i\gets \gamma \widehat{x_i} +\beta\equiv BN_{r,\beta}(x_i) yi←γxi +β≡BNr,β(xi),这个操作可以增强模型的 capacity,也就是让模型自己判断是否要对数据进行标准化,进行多大程度的标准化。如果
γ = σ B 2 , β = μ B \gamma=\sqrt{\sigma_B^2}, \beta=\mu_B γ=σB2,β=μB,那么就实现了恒等映射(前三步做标准化,这步做标准化的反变换)。
Batch Normalization 层一般在激活函数前一层。
在 PyTorch 中,有 3 个 Batch Normalization 类:
- nn.BatchNorm1d(),输入数据的形状是 B × C × 1 D f e a t u r e ( L ) B \times C \times 1D feature(L) B×C×1Dfeature(L) :length
- nn.BatchNorm2d(),输入数据的形状是 B × C × 2 D f e a t u r e ( H × W ) B \times C \times 2D feature(H \times W) B×C×2Dfeature(H×W) :hight, weight
- nn.BatchNorm3d(),输入数据的形状是 B × C × 3 D f e a t u r e ( T × H × W ) B \times C \times 3D feature(T \times H \times W) B×C×3Dfeature(T×H×W) :time, hight, weight
torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
num_features:一个样本的
特征维度C,这个参数最重要
eps:在进行标准化操作时的分布修正项
momentum:指数加权平均估计当前的均值和方差
affine:是否需要 affine transform,默认为 True
track_running_stats:True 为训练状态,此时均值和方差会根据每个 mini-batch 改变。False 为测试状态,此时均值和方差会固定
例如,输入数据的形状是 B × C × 2 D f e a t u r e B \times C \times 2D feature B×C×2Dfeature,(3, 2, 2, 2, 3),表示一个 mini-batch 有 3 个样本,每个样本有 2 个特征,每个特征的维度是 2 x 2 x3。那么就会计算 2 个均值和方差,分别对应每个特征维度。momentum 设置为 0.3,第一次的均值和方差默认为 0 和 1。输入两次 mini-batch 的数据。
Layer Normalization
提出的原因:Batch Normalization 不适用于变长的网络,如 RNN
思路:每个网络层计算均值和方差, γ \gamma γ和 β \beta β 为逐样本的可学习参数。
torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)
normalized_shape:该层每个样本特征的形状,可以取 C × H × W C \times H \times W C×H×W、 H × W H \times W H×W、 W W W
eps:标准化时的分母修正项
elementwise_affine:是否需要逐个样本 affine transform
例如,输入数据的形状是 B × C × f e a t u r e B \times C \times feature B×C×feature,(8, 2, 3, 4),表示一个 mini-batch 有 8 个样本,每个样本有 2 个特征,每个特征的维度是 3 x 4。那么就会计算 8 个均值和方差,分别对应每个样本。
相关文章:

Normalization(BN and LN) in NN
Batch Normalization 称为批标准化。批是指一批数据,通常为 mini-batch;标准化是处理后的数据服从 N ( 0 , 1 ) N(0,1) N(0,1) 的正态分布。在训练过程中,数据需要经过多层的网络,如果数据在前向传播的过程中,尺度发…...
opencv-22 图像几何变换01-缩放-cv2.resize()(图像增强,图像变形,图像拼接)
什么是几何变换? 几何变换是计算机图形学中的一种图像处理技术,用于对图像进行空间上的变换,而不改变图像的内容。这些变换可以通过对图像中的像素位置进行调整来实现。 常见的几何变换包括: 平移(Translation&#x…...

python机器学习(五)逻辑回归、决策边界、代价函数、梯度下降法实现线性和非线性逻辑回归
线性回归所解决的问题是把数据集的特征传入到模型中,预测一个值使得误差最小,预测值无限接近于真实值。比如把房子的其他特征传入到模型中,预测出房价, 房价是一系列连续的数值,线性回归解决的是有监督的学习。有很多场…...
, AsQueryable() ,.ToList(),的区别和用法)
聊聊Linq中.AsEnumerable(), AsQueryable() ,.ToList(),的区别和用法
聊聊Linq中.AsEnumerable(), AsQueryable() ,.ToList(),的区别和用法 当使用LINQ查询数据时,我们常常会面临选择使用.AsEnumerable(), .AsQueryable(), 和 .ToList()方法的情况。这些方法在使用时有不同的效果和影响,需要根据具体场景来选择合适的方法。…...

【机器学习】机器学习中的“本体”概念
一、说明 在机器学习中,本体越来越多地用于提供基于相似性分析和场景知识的 ML 模型。 在传统的基于标签的定义中,对象往往是孤立的,可扩展性差,存在重复的可能性,对象之间的关系无法体现。在基于本体的定义中…...

ChatGPT是否能够进行对话中的参考和指代解析?
ChatGPT在对话中的参考和指代解析方面有一定的潜力,但需要针对具体任务和上下文进行定制和优化。参考和指代解析是指理解对话中的代词、名词短语等表达方式所指代的具体对象或信息。在对话中,参考和指代解析对于理解上下文、保持对话连贯性和生成准确回复…...
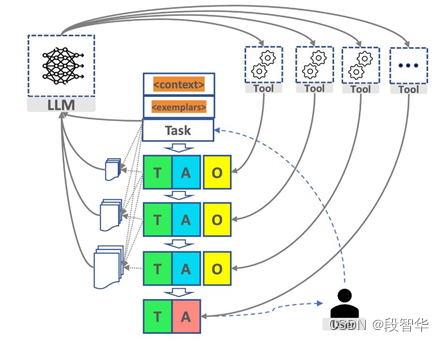
网红项目AutoGPT源码内幕及综合案例实战(三)
AutoGPT on LangChain PromptGenerator等源码解析 本节阅读AutoGPT 的prompt_generator.py源代码,其中定义了一个PromptGenerator类和一个get_prompt函数,用于生成一个提示词信息。PromptGenerator类提供了添加约束、命令、资源和性能评估等内容的方法,_generate_numbered_l…...

第八章:list类
系列文章目录 文章目录 系列文章目录前言list的介绍及使用list的介绍list的使用list的构造函数list的迭代器list的容量list的成员访问list的增删改查 list与vector的对比总结 前言 list是STL的一种链表类,可以在常数范围内在任意位置进行插入和删除的序列式容器。 …...

VUE声音-报警-实现方式
1.先准备一个mp3文件包:(这个24小时生效如果失效可留言,看到就会增加时效) 获取mp3地址: https://www.aliyundrive.com/t/uQ8zqjn9JKSfm7QlGOSr2.代码内容 进入页面就会自动 播放mp3的内容信息了。 <template>…...

【Coppeliasim C++】焊接机械臂仿真
项目思维导图 该项目一共三个demo: 机械臂末端走直线 2. 变位机转台转动 3.机械臂末端多点样条运动 笔记: 基于等级的蚁群系统在3D网格地图中搜索路径的方法: 基于等级的蚁群系统(Hierarchical Ant Colony System,HACS)是一种改进的蚁群优化算法。它在传…...

【LeetCode】94.二叉树的中序遍历
题目 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。 示例 1: 输入:root [1,null,2,3] 输出:[1,3,2]示例 2: 输入:root [] 输出:[]示例 3: 输入:root [1] 输…...
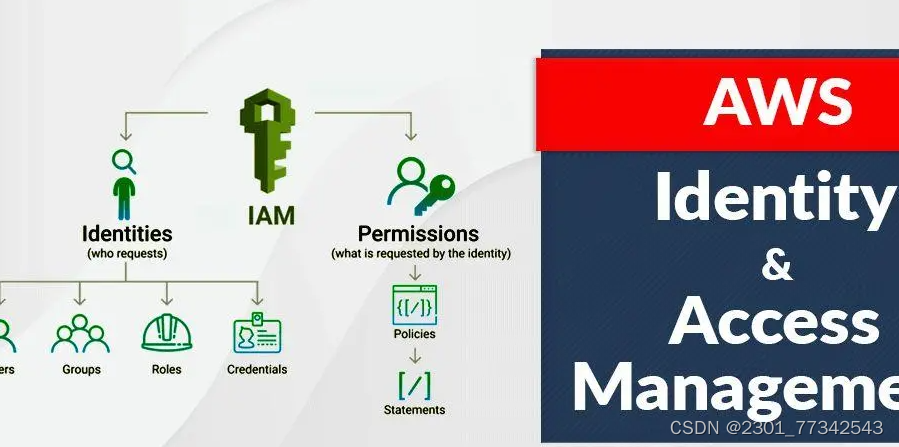
AWS IAM介绍
前言 AWS是世界上最大的云服务提供商,它提供了很多组件供消费者使用,其中进行访问控制的组件叫做IAM(Identity and Access Management), 用来进行身份验证和对AWS资源的访问控制。 功能 IAM的功能总结来看,主要分两种࿱…...
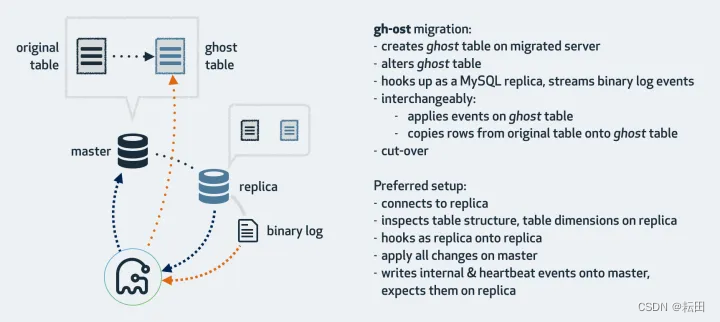
MySQL碎片清理
为什么产生? 经过大量增删改的表,都可能存在碎片 MySQL数据结构是B树, 删除某一记录,只会标记为删除,后续插入一条该区间的记录,就会复用这个位置。 删除整个数据页的记录,则整个页标记为“可…...

elasticsearch操作(API方式)
说明:es操作索引库、文档,除了使用它们自带的命令外(参考:http://t.csdn.cn/4zpmi),在IDEA中可以添加相关的依赖,使用对应的API来操作。 准备工作 搭建一个SpringBoot项目,DAO使用…...

Vue2.0 使用 echarts
目录 1. 配置 渲染2. 数据渲染 1. 配置 渲染 安装 echarts 依赖 npm install echarts -Smain.js,引入 echarts import * as echarts from echarts// 在import的后面,echarts的前面加一个 * as Vue.prototype.$echarts echarts从 echarts 官网直接复制…...

企业微信,阿里钉钉告警群机器人
链接:如何通过企业微信群接收报警通知_云监控-阿里云帮助中心...

linux下的tomcat
springboot项目端口是8080,部署到linux运行之后,为什么能检测到tomcat 手动安装tomcat,以下是在 Linux 系统上安装 Tomcat 的步骤: 下载 Tomcat 安装包。您可以从 Tomcat 官方网站(https://tomcat.apache.org/ ↗&…...

Vue源码学习 - new Vue初始化都做了什么?
目录 前言一、创建一个 Vue 实例二、找到 Vue 构造函数三、源码分析 - Vue.prototype._init四、源码分析 - 调用 $mount 方法,进入挂载阶段五、总结 前言 使用Vue也有一段时间了,最近去阅读了Vue的源码,想总结分享下学到的新东西。 如果觉得…...
新零售数字化商业模式如何建立?新零售数字化营销怎么做?
随着零售行业增速放缓、用户消费结构升级,企业需要需求新的价值增长点进行转型升级,从而为消费者提供更为多元化的消费需求、提升自己的消费体验。在大数据、物联网、5G及区块链等技术兴起的背景下,数字化新零售系统应运而生。 开利网络认为&…...
C++语法(26)--- 特殊类设计
C语法(25)--- 异常与智能指针_哈里沃克的博客-CSDN博客https://blog.csdn.net/m0_63488627/article/details/131537799?spm1001.2014.3001.5501 目录 1.特殊类设计 1.设计一个类,不能被拷贝 C98 C11 2.设计一个类,只能在堆上…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
