蓝桥杯专题-真题版含答案-【垒骰子_动态规划】【抽签】【平方怪圈】【凑算式】
- 点击跳转专栏=>Unity3D特效百例
- 点击跳转专栏=>案例项目实战源码
- 点击跳转专栏=>游戏脚本-辅助自动化
- 点击跳转专栏=>Android控件全解手册
- 点击跳转专栏=>Scratch编程案例
- 点击跳转=>软考全系列
- 点击跳转=>蓝桥系列
👉关于作者
专注于Android/Unity和各种游戏开发技巧,以及各种资源分享(网站、工具、素材、源码、游戏等)
有什么需要欢迎底部卡片私我,获取更多支持,交流让学习不再孤单。

👉实践过程
需要所有整理的文档可底部卡片联系我,直接发压缩包。
😜垒骰子_动态规划
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。
经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。
atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦~
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 数字不能紧贴在一起。
「输出格式」
一行一个数,表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
#define MOD 1000000007#include <map>
#include <vector>
#include <iostream>using namespace std;long long dp[2][7];//dp[i][j]表示有i层,限定朝上的数字为j的稳定方案数
int n, m;
bool conflict[7][7];
map<int, int> op;void init() {op[1] = 4;op[4] = 1;op[2] = 5;op[5] = 2;op[3] = 6;op[6] = 3;
}int main(int argc, const char *argv[]) {init();scanf("%d %d", &n, &m);for (int i = 0; i < m; ++i) {int a, b;scanf("%d %d", &a, &b);conflict[a][b] = true;conflict[b][a] = true;}
// 输入完成for (int j = 1; j <= 6; ++j) {dp[0][j] = 1;}int cur = 0;
// 迭代层数for (int level = 2; level <= n; ++level) {cur = 1 - cur;
// 尝试将6个面放在当前一层朝上的方向for (int j = 1; j <= 6; ++j) {dp[cur][j] = 0;
// 将与op[j]不冲突的上一层格子里面的数累加起来for (int i = 1; i <= 6; ++i) {if (conflict[op[j]][i])continue;//冲突的面朝上是不可取的dp[cur][j] = (dp[cur][j] + dp[1 - cur][i]) % MOD;}}}long long sum = 0;for (int k = 1; k <= 6; ++k) {sum = (sum + dp[cur][k]) % MOD;}// 快速幂,求4的n次方long long ans = 1;long long tmp = 4;long long p = n;while (p != 0) {if (p & 1 == 1) ans = (ans * tmp) % MOD;tmp = (tmp * tmp) % MOD;p >>= 1;}printf("%d\n", (sum * ans) % MOD);return 0;
}
😜抽签
X星球要派出一个5人组成的观察团前往W星。
其中:
A国最多可以派出4人。
B国最多可以派出2人。
C国最多可以派出2人。
…
那么最终派往W星的观察团会有多少种国别的不同组合呢?
下面的程序解决了这个问题。
数组a[] 中是每个国家可以派出的最多的名额。
程序执行结果为:
DEFFF
CEFFF
CDFFF
CDEFF
CCFFF
CCEFF
CCDFF
CCDEF
BEFFF
BDFFF
BDEFF
BCFFF
BCEFF
BCDFF
BCDEF
…
(以下省略,总共101行)
#include <stdio.h>
#define N 6
#define M 5
#define BUF 1024
void f(int a[], int k, int m, char b[])
{
int i,j;
if(k==N){b[M] = 0;if(m==0) printf("%s\n",b);return;
}for(i=0; i<=a[k]; i++){for(j=0; j<i; j++) b[M-m+j] = k+'A';______________________; //填空位置
}
}
int main()
{
int a[N] = {4,2,2,1,1,3};
char b[BUF];
f(a,0,M,b);
return 0;
}
#include <stdio.h>
#define N 6
#define M 5
#define BUF 1024
int ans;
/** k=a数组的下标,* m代表人数,初始为5* b字符串*/
void f(int a[], int k, int m, char b[])
{int i,j;if(k==N){b[M] = 0;//字符串结尾的标志if(m==0) {printf("%s\n",b);ans++;}return;}for(i=0; i<=a[k]; i++){//试着将k国家,派出i人for(j=0; j<i; j++) //填充buf,有i人就填i个国家符号(k+'A')b[M-m+j] = k+'A';
// ______________________; //填空位置f(a,k+1,m-i,b);}
}
int main()
{int a[N] = {4,2,2,1,1,3};char b[BUF];f(a,0,M,b);printf("%d\n",ans);return 0;
}
😜平方怪圈
如果把一个正整数的每一位都平方后再求和,得到一个新的正整数。
对新产生的正整数再做同样的处理。
如此一来,你会发现,不管开始取的是什么数字,
最终如果不是落入1,就是落入同一个循环圈。
请写出这个循环圈中最大的那个数字。
请填写该最大数字。
#include <iostream>
#include <sstream>
using namespace std;int extract(int start){string str;stringstream ss;ss<<start;ss>>str;int ans=0;for (int i = 0; i < str.length(); ++i) {ans+=(str[i]-'0')*(str[i]-'0');}return ans;
}
int main(int argc, const char * argv[]) {int start=3;int cnt=0;while(cnt<1000){cout<<start<<endl;int sum =extract(start);start=sum;cnt++;}return 0;
}
😜凑算式
B DEF
A + --- + ------- = 10C GHI
这个算式中AI代表19的数字,不同的字母代表不同的数字。
比如:
6+8/3+952/714 就是一种解法,
5+3/1+972/486 是另一种解法。
这个算式一共有多少种解法?
#include <iostream>
#include <cmath>
using namespace std;
int a[]={1,2,3,4,5,6,7,8,9};int ans;
bool check(){int x = a[3] * 100 + a[4] * 10 + a[5];int y = a[6] * 100 + a[7] * 10 + a[8];if((a[1] * y + a[2] * x) % (y * a[2])==0 && a[0] + (a[1] * y + a[2] * x) / (y * a[2]) == 10)return true;return false;
}
/*递归回溯生成全排列,适用于无重复元素的情况* 考虑第k位,前面已经排定*/
void f(int k) {if(k==9){//一种排列已经生产if(check())ans++;}
// 从k往后的每个数字都可以放在k位for (int i = k; i < 9; ++i) {{int t=a[i];a[i]=a[k];a[k]=t;}f(k+1);//递归{int t=a[i];a[i]=a[k];a[k]=t;}//回溯}
}
int main(int argc, const char * argv[]) {
// f(0);do{if(check())ans++;}while(next_permutation(a,a+9));cout<<ans<<endl;return 0;
}
👉其他
📢作者:小空和小芝中的小空
📢转载说明-务必注明来源:https://zhima.blog.csdn.net/
📢这位道友请留步☁️,我观你气度不凡,谈吐间隐隐有王者霸气💚,日后定有一番大作为📝!!!旁边有点赞👍收藏🌟今日传你,点了吧,未来你成功☀️,我分文不取,若不成功⚡️,也好回来找我。
温馨提示:点击下方卡片获取更多意想不到的资源。

相关文章:

蓝桥杯专题-真题版含答案-【垒骰子_动态规划】【抽签】【平方怪圈】【凑算式】
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例点击跳转>软考全系列点击跳转>蓝桥系列 👉关于作者 专注于Android/Unity和各种游…...

kubernetes调试利器——kubectl debug工具
通常情况下,业务容器所使用的镜像是非常精简的,而一旦业务容器出现问题,通过kubectl exec进入到容器时,我们会发现自己需要使用的工具都没有,也无法通过apt, apt-get, yum等包管理工具下载需要的工具。 想要解决这个尴…...

浅谈es5如何保证并发请求的返回顺序
最近在公司实习写的是es5,在和回调地狱经过一番拉扯之后写下这篇文章,也算是体验了一把没有promise的时代 假设我们的div有一个日历列表,但是由于大小关系只能每次显示2天的信息,项目限制只能使用es5,不能使用es6的pro…...

深入浅出Pytorch函数——torch.squeeze
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 深入浅出Pytorch函数——torch.squeeze 深入浅出Pytorch函数——torch.unsqueeze 将输入张量形状为1的维度去除并返回。比如输入向量的形状为 A 1 B 1 C 1 D A\times1\times B\times1\times C…...

【LeetCode】121.买卖股票的最佳时机
题目 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的最大…...

【力扣】74. 搜索二维矩阵 <二分法>
【力扣】74. 搜索二维矩阵 给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非递减顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则&am…...

Spring Task+Cron表达式
不需要导入坐标spring-context(包含在了spring-boot-starter) 在启动类添加EnableScheduleing开启任务调度 单独建个定时任务包task,创建定时任务类MyTask 在定时任务类添加Component 在类的方法上添加Scheduled(cron “cron表达…...

你们公司的【前端项目】是如何做测试的?字节10年测试经验的我这样做的...
前端项目也叫web端项目(通俗讲就是网页上的功能)是我们能够在屏幕上看到并产生交互的体验。 前端项目如何做测试? 要讲清楚这个问题,先需要你对测试流程现有一个全局的了解,先上一张测试流程图: 测试流程…...
华为战略方法论:BLM模型之关键任务与依赖关系
内容简介 在 BLM 模型中,执行部分包括四个模块,分别是: 关键任务与依赖关系;组织与绩效;人才;氛围与文化。 详细内容,大家可以参看下面这张图。 这四个模块其实是可以进一步划分成两个关键点…...

django的ORM模板的fake更新
django存量数据表的migraions记录丢失,若要更新表结构,则需用到fake,否则报错: 解决步骤如下: 1)同步存量表结构,生成伪表 --fake sudo python3 manage.py makemigrations appname sudo pyt…...
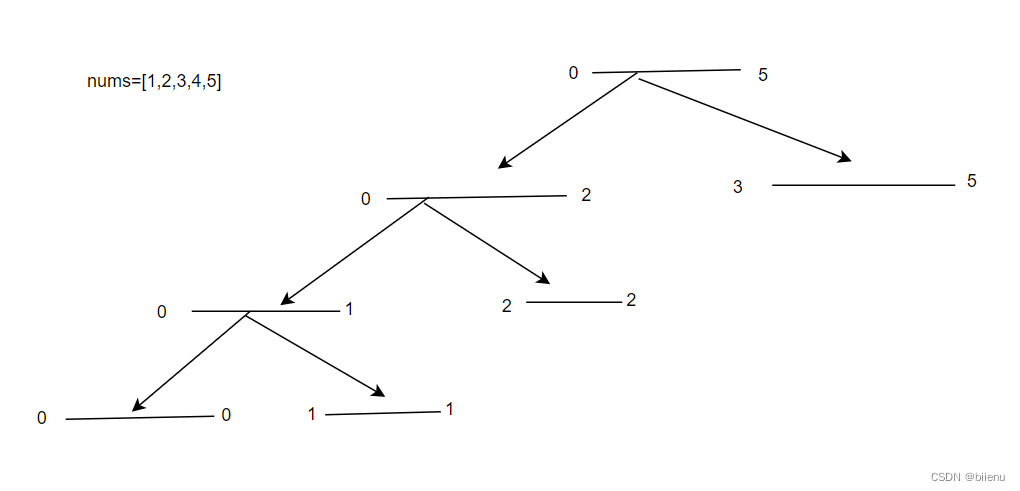
239.滑动窗口最大值
leetcode原题链接 题目描述: 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例1: 输入:nums [1,…...

Redis基础原理
1 概念 1.1 关系型数据库与非关系型数据库对比 关系型数据库Mysql、Oralce特点数据之间有关联;数据存储在硬盘上效率操作关系型数据库非常耗时 非关系型数据库redis、hbase存储key:value特点数据之间没有关联关系;数据存储在内存中缓存思想从缓存中获…...

.NET 5 Web API 中JWT详细教程:保护你的Web应用
第一部分: 理解JWT JSON Web Token(JWT)是一种在不同系统之间传递信息的安全方式。它由三部分组成:头部(Header)、载荷(Payload)和签名(Signature)。头部包…...
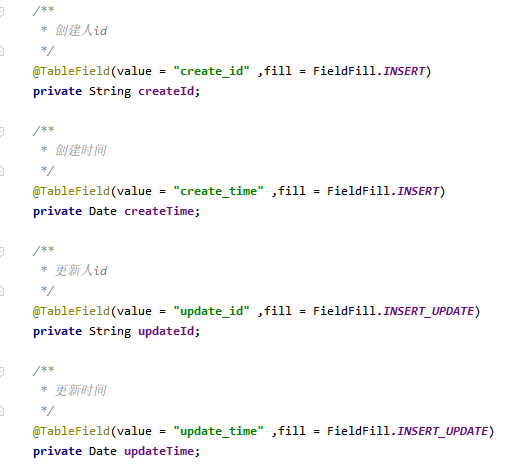
MyBatis-Plus自动填充
文章目录 一、前言二、MyBatis-Plus自动填充功能实现2.1、实体类上增加注解2.2、自定义填充类编写 一、前言 我们在建表的时候,所有的表都会有create_id(创建人id)、create_time(创建时间)、update_id(更新…...

Dubbo服务提供者失效踢出原理解析
Dubbo服务提供者失效踢出原理解析 在分布式系统中,服务提供者的失效是一个常见而且重要的问题。Dubbo作为一款优秀的分布式服务框架,提供了失效踢出机制来及时剔除不可用的服务提供者,确保系统的稳定性和可用性。本文将深入探讨Dubbo服务提供…...

el-select下拉框处理分页数据,触底加载更多
1、声明自定义指令: directives: {loadmore: {inserted(el, binding) {const SELECTWRAP_DOM el.querySelector(.el-select-dropdown .el-select-dropdown__wrap);SELECTWRAP_DOM.addEventListener(scroll, function() {const condition this.scrollHeight - thi…...

如何设计自动化测试脚本?一文5个步骤带你从0到1设计
企业中如何设计自动化测试脚本呢?今天我们就来为大家分享一些干货。 一、线性设计 线性脚本设计方式是以脚本的方式体现测试用例,是一种非结构化的编码方式,多数采用录制回放的方式,测试工程师通过录制回访的访问对被测系统进行自…...

PostgreSQL实战-数据库迁移部署
PostgreSQL实战-数据库迁移部署 介绍 根据项目需求,我们需要将现有的PostgreSQL数据库重新部署到新的服务器上。由于项目本身就是基于PostgreSQL数据库构建的,因此数据库迁移将变得十分便捷。接下来,我将简要介绍我们的迁移步骤。 迁移步骤…...

PHP数据库
PHP MySQL 连接数据库 MySQL 简介MySQL Create 免费的 MySQL 数据库通常是通过 PHP 来使用的。 连接到一个 MySQL 数据库 在您能够访问并处理数据库中的数据之前,您必须创建到达数据库的连接。 在 PHP 中,这个任务通过 mysql_connect() 函数完成。 …...
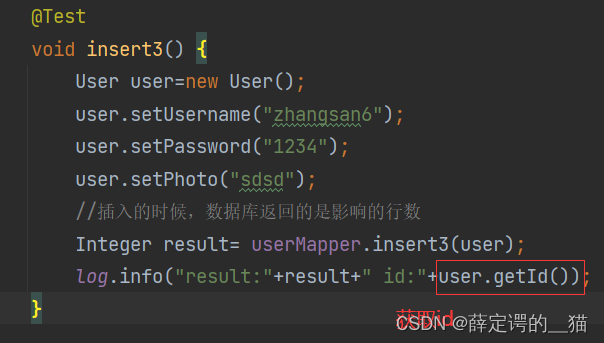
Mybatis的基本操作--增删改查
目录 查看数据 无参数 一个参数 多个参数 添加数据 修改数据 删除数据 注释的方式进行查找数据 查看数据 分三种情况:无参,有一个参数,有多个参数的情况。 (这里的详细操作步骤是博主的上一篇博客写的:初识My…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
