【深度学习】激活函数
上一章——认识神经网络
新课P54介绍了强人工智能概念,P55到P58解读了矩阵乘法在代码中的应用,P59,P60介绍了在Tensflow中实现神经网络的代码及细节,详细的内容可以自行观看2022吴恩达机器学习Deeplearning.ai课程,专栏中就不再赘述。
文章目录
- 激活函数的替代方案
- Sigmoid函数
- ReLU函数
- 线性函数
- 激活函数的选择
- Output层
- 隐藏层
- 为什么模型需要激活函数
激活函数的替代方案
Sigmoid函数
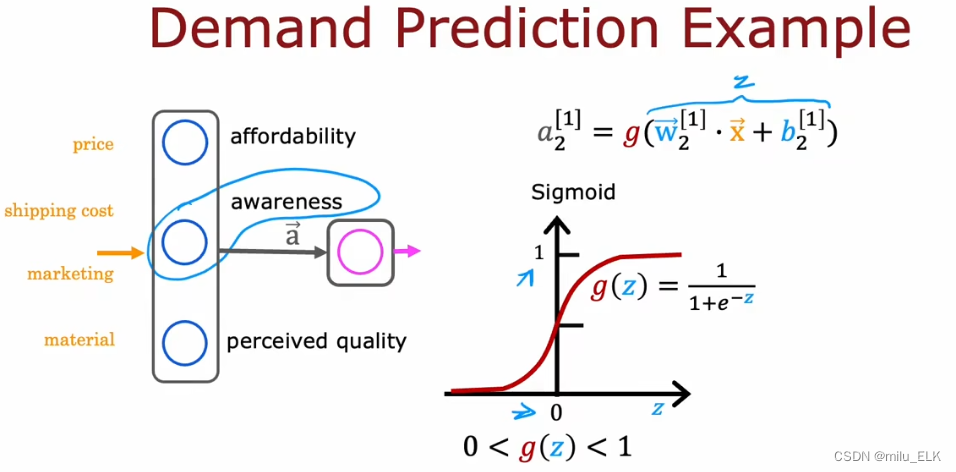
在逻辑回归中,我们使用的激活函数是Sigmoid函数,又称逻辑函数,它能预测(0,1)区间内的值,因此我们常常会在二分问题中使用。
ReLU函数

如果我们想要取到更大的正值,我们可以使用这个激活函数来代替,如图右边所示。
这个函数称为ReLU函数(Rectified Linear Unit),即修正线性单元,ReLU:g(z)=max(0,z)ReLU:g(z)=max(0,z)ReLU:g(z)=max(0,z)
其中当z<0z<0z<0时,g(z)=0g(z)=0g(z)=0,z>0z>0z>0时,g(z)=zg(z)=zg(z)=z
在实际工作中,ReLU函数的使用会更加广泛一些,
线性函数

线性激活函数g(z)=zg(z)=zg(z)=z,我们也可以称它没有使用任何激活函数,因为输入量为z,输出激活量a=g(z)=za=g(z)=za=g(z)=z,实际上没有任何变化。
激活函数的选择
激活函数如何选择取决于你需要一个什么样的输出量,我们以上面提到的几种激活函数为例
Output层

如果你要选择输出层的激活函数,那么最后得到的就是想要预测的结果,假如你想要预测的结果是一个二分问题,那么其预测值应当是处于0,1之间的,我们会选择逻辑函数;
假如你是要预测股票的涨跌,那么股票的跌可以视为负数,涨视为正数,因此你的输出层激活函数需要有正有负,我们就会选择线性激活函数,使得它有负值。
假设你要预测房价,那么房价一定不会是负数,我们不接受负值的出现,因此你可以选择ReLU函数来进行预测。
以上只是举我们讲过的几种激活函数为例,总而言之需要根据实际要求来选择激活函数,
以上仅是针对输出层,并不对隐藏层适用。
隐藏层
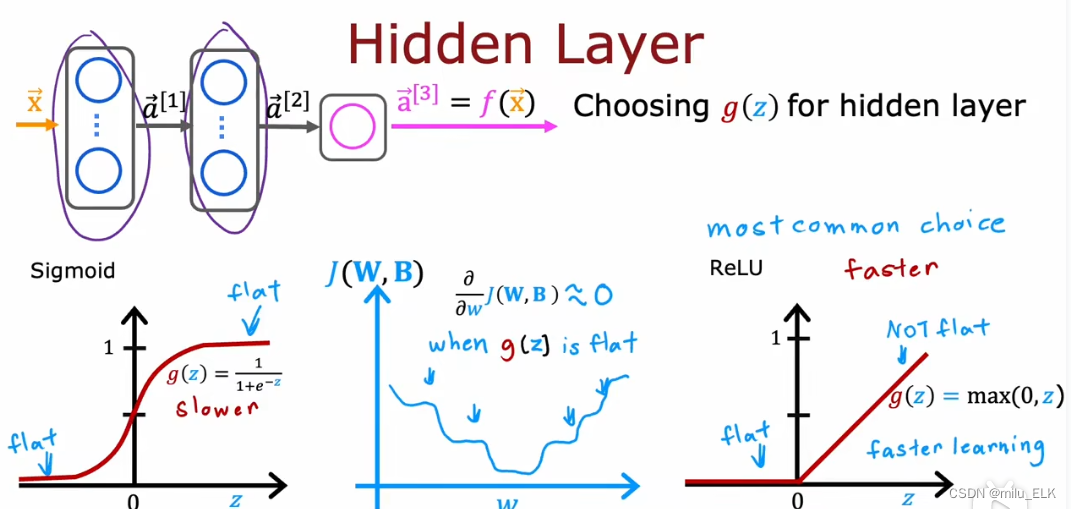 在上一节介绍神经网络的时候,隐藏层使用的是Sigmoid函数,然而实际上ReLU或者其他函数更好,
在上一节介绍神经网络的时候,隐藏层使用的是Sigmoid函数,然而实际上ReLU或者其他函数更好,
- ReLU函数的计算比Sigmoid更简单,更快速
- ReLU函数的梯度下降速度比Sigmoid更快
如果仔细观察Sigmoid函数的代价函数(上图蓝色部分函数),会发现Sigmoid的函数形状并不是很适合梯度下降,并且随着Z的增大或缩小,Sigmoid函数的图像会趋于平坦,这就导致了dJdw≈0\frac{dJ}{dw}≈0dwdJ≈0,从而导致了梯度下降速度会越来越慢,而ReLU函数不会有这样的问题。一般来说,大部分情况下在隐藏层用ReLU函数都会更好。
为什么模型需要激活函数
我们的模型能不能不使用任何激活函数(仅线性激活函数)?答案是否定的,首先,从建立神经网络的目的来看,设置激活函数的目的就是为了向神经元添加非线性的输入来实现更复杂的计算,如果不使用激活函数,那么也没必要使用神经网络。
如果神经网络不使用激活函数,会发生什么情况?如下图所示
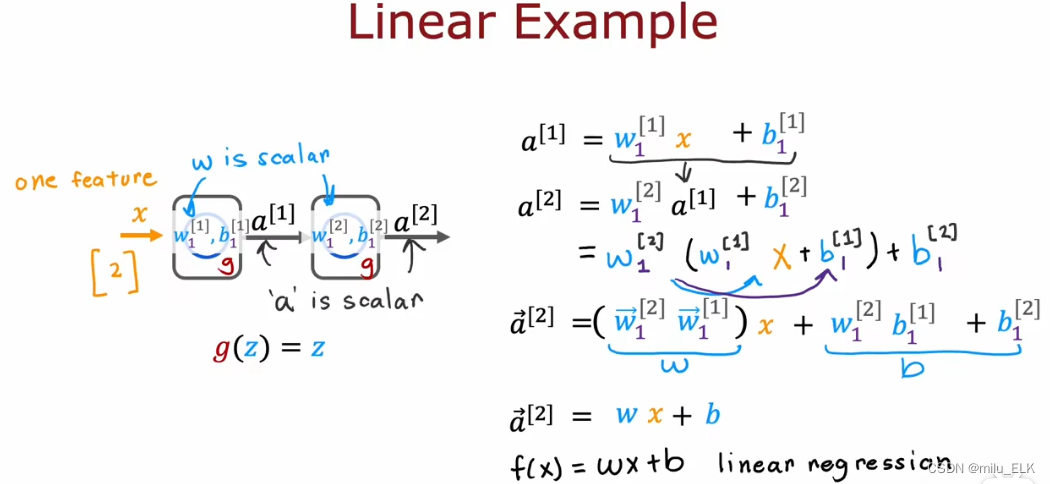
假设我们的神经网络的隐藏层和输出层使用的全部都是线性激活函数,那么
a[1]=w1[1]x+b1[1]a^{[1]}=w^{[1]}_1x +b^{[1]}_1a[1]=w1[1]x+b1[1], a[2]=w1[2]a[1]+b1[2]a^{[2]}=w^{[2]}_1a^{[1]} +b^{[2]}_1a[2]=w1[2]a[1]+b1[2]
我们将a[2]a^{[2]}a[2]式子中的a[1]a^{[1]}a[1]替换,就能得到a[2]=w1[2](w1[1]x+b1[1])+b1[2]a^{[2]}=w^{[2]}_1(w^{[1]}_1x +b^{[1]}_1) +b^{[2]}_1a[2]=w1[2](w1[1]x+b1[1])+b1[2]
展开后得到a[2]=(w1[2]w1[1])x+w1[2]b1[1]+b1[2]a^{[2]}=(w^{[2]}_1w^{[1]}_1)x +w^{[2]}_1b^{[1]}_1 +b^{[2]}_1a[2]=(w1[2]w1[1])x+w1[2]b1[1]+b1[2],将(w1[2]w1[1])设为w,(w1[2]b1[1]+b1[2])设为b就得到了a[2]=wx+b(w^{[2]}_1w^{[1]}_1)设为w,(w^{[2]}_1b^{[1]}_1 +b^{[2]}_1)设为b就得到了 a^{[2]}=wx +b(w1[2]w1[1])设为w,(w1[2]b1[1]+b1[2])设为b就得到了a[2]=wx+b
也就是说,经过了两层的线性函数的计算,实际上也就相当于进行一次线性函数计算,那么n层线性激活函数的神经网络实际只相当于进行一次线性函数计算。也就是说如果不采用任何激活函数,整个神经网络和线性函数没有差别。所以,如果不使用激活函数,神经网络并不能提升进行复杂计算的能力,整个模型相当于逻辑回归。
在未来的学习中,我们也会接触到其他的激活函数,理解激活函数的作用,选择适宜的激活函数,将对我们神经网络的搭建具有重大意义。
下一章——多分类问题
相关文章:

【深度学习】激活函数
上一章——认识神经网络 新课P54介绍了强人工智能概念,P55到P58解读了矩阵乘法在代码中的应用,P59,P60介绍了在Tensflow中实现神经网络的代码及细节,详细的内容可以自行观看2022吴恩达机器学习Deeplearning.ai课程,专…...
)
【新2023】华为OD机试 - 数字的排列(Python)
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 数字的排列 题目 小华是个很有对数字很敏感的小朋友, 他觉得数字的不同排列方式有特殊的美感。 某天,小华突发奇想,如果数字多行排列, 第一行1个数, 第二行2个, 第三行3个, 即第n行n个数字,并且…...

[oeasy]python0085_ASCII之父_Bemer_COBOL_数据交换网络
编码进化 回忆上次内容 上次 回顾了 字符编码的 进化过程 IBM 在数字化过程中 作用 非常大IBM 的 BCDIC 有 黑历史 😄 6-bit的 BCDIC 直接进化成 8-bit的 EBCDIC补全了 小写字母 和 控制字符 在ibm就是信息产业的年代 ibm的标准 怎么最终 没有成为 行业的标准 呢…...

volatile,内存屏障
volatile的特性可见性: 对于其他线程是可见,假设线程1修改了volatile修饰的变量,那么线程2是可见的,并且是线程安全的重排序: 由于CPU执行的时候,指令在后面的会先执行,在指令层级的时候我们晓得volatile的特性后,我们就要去volatile是如何实现的,这个很重要!&#…...

【ESP 保姆级教程】玩转emqx MQTT篇① —— 系统主题、延迟发布、服务器配置预算、常见问题
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-18 ❤️❤️ 本篇更新记录 2023-02-18 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...
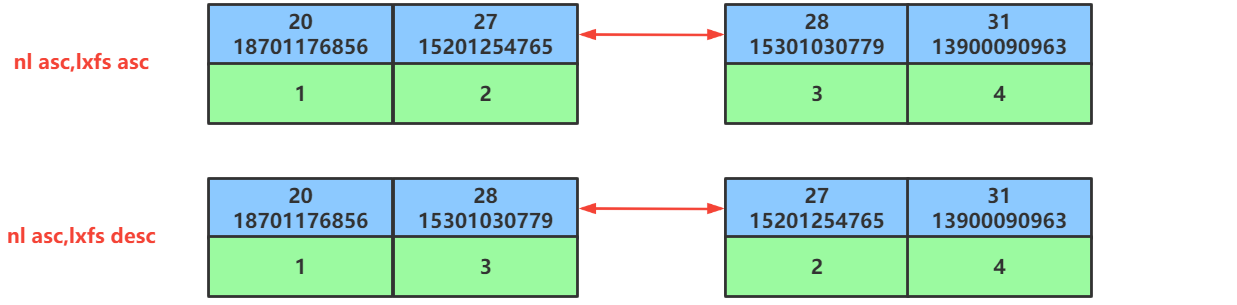
第48讲:SQL优化之ORDER BY排序查询的优化
文章目录1.ORDEY BY排序查询优化方面的概念2.ORDER BY排序的优化原则3.ORDER BY排序优化的案例3.1.准备排序优化的表以及索引3.2.同时对nl和lxfs字段使用升序排序3.3.同时对nl和lxfs字段使用降序排序3.4.排序时调整联合索引中字段的位置顺序3.5.排序时一个字段使用升序一个字段…...
[Datawhale][CS224W]图机器学习(三)
目录一、简介与准备二、教程2.1 下载安装2.2 创建图2.2.1 常用图创建(自定义图创建)1.创建图对象2.添加图节点3.创建连接2.2.2 经典图结构1.全连接无向图2.全连接有向图3.环状图4.梯状图5.线性串珠图6.星状图7.轮辐图8.二项树2.2.3 栅格图1.二维矩形栅格…...

2023版最新最强大数据面试宝典
此套面试题来自于各大厂的真实面试题及常问的知识点,如果能理解吃透这些问题,你的大数据能力将会大大提升,进入大厂指日可待!目前已经更新到第4版,广受好评!复习大数据面试题,看这一套就够了&am…...

CSS 中的 BFC 是什么,有什么作用?
BFC,即“块级格式化上下文”(Block Formatting Context),是 CSS 中一个重要的概念,它指的是一个独立的渲染区域,让块级盒子在布局时遵循一些特定的规则。BFC 的存在使得我们可以更好地控制文档流࿰…...

总结在使用 Git 踩过的坑
问题一: 原因 git 有两种拉代码的方式,一个是 HTTP,另一个是 ssh。git 的 HTTP 底层是通过 curl 的。HTTP 底层基于 TCP,而 TCP 协议的实现是有缓冲区的。 所以这个报错大致意思就是说,连接已经关闭,但是此时有未处理…...

从 HTTP 到 gRPC:APISIX 中 etcd 操作的迁移之路
罗泽轩,API7.ai 技术专家/技术工程师,Apache APISIX PMC 成员。 原文链接 Apache APISIX 现有基于 HTTP 的 etcd 操作的局限性 etcd 在 2.x 版本的时候,对外暴露的是 HTTP 1 (以下简称 HTTP)的接口。etcd 升级到 3.x…...
【C语言每日一题】——倒置字符串
【C语言每日一题】——倒置字符串😎前言🙌倒置字符串🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者简…...

Native扩展开发的一般流程(类似开发一个插件)
文章目录大致开发流程1、编写对应的java类服务2、将jar包放到对应位置3、配置文件中进行服务配置4、在代码中调用5、如何查看服务调用成功大致开发流程 1、编写服务,打包为jar包2、将jar包放到指定的位置3、在配置文件中进行配置,调用对应的服务 1、编…...

【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 任务调度 题目 现有一个 CPU 和一些任务需要处理,已提前获知每个任务的任务 ID、优先级、所需执行时间和到达时间。 CPU 同时只能运行一个任务,请编写一个任务调度程序,采用“可抢占优先权调度”调度…...
Spring3定时任务
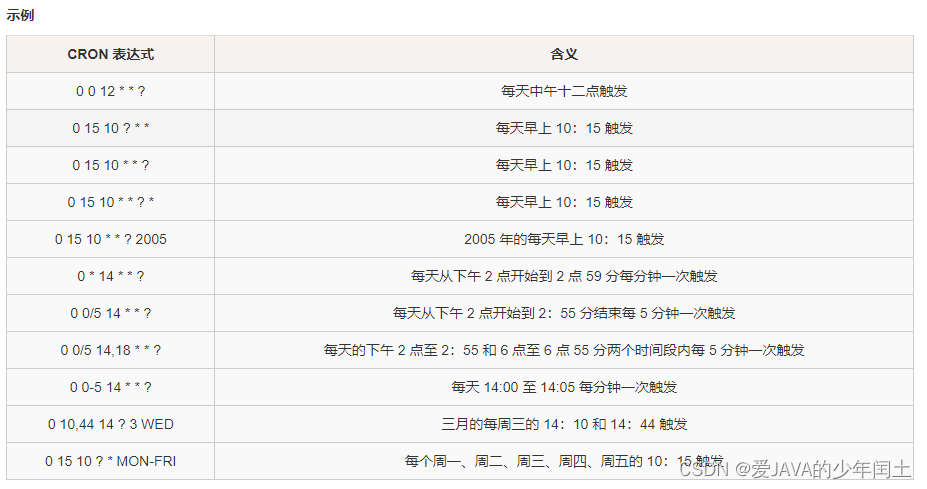
简介 Spring 内部有一个 task 是 Spring 自带的一个设定时间自动任务调度,提供了两种方式进行配置,一种是注解的方式,而另外一种就是 XML 配置方式了;注解方式比较简洁,XML 配置方式相对而言有些繁琐,但是应用场景的不…...
数据库版本管理工具Flyway应用研究
目录1 为什么使用数据库版本控制2 数据库版本管理工具选型:Flyway、Liquibase、Bytebase、阿里 DMSFlywayLiquibaseBytebase阿里 DMS3 Flyway数据库版本管理研究3.1 参考资料3.2 Flyway概述3.3 Flyway原理3.4 Flyway版本和功能3.5 Flyway概念3.5.1 版本迁移…...

更换 Ubuntu 系统 apt 命令安装软件源
更换 Ubuntu 系统 apt 命令安装软件源清华大学开源软件镜像站 https://mirrors.tuna.tsinghua.edu.cn/ 1. Ubuntu 的软件源配置文件 /etc/apt/sources.list MIRRORS -> 使用帮助 -> ubuntu https://mirrors.tuna.tsinghua.edu.cn/help/ubuntu/ Ubuntu 系统 apt 命令安…...
2023年可见光通信(LiFi)研究新进展
可见光无线通信Light Fidelity(LiFi)又称“光保真技术”,是一种利用可见光进行数据传输的全新无线传输技术。LiFi是一种以半导体光源作为信号发射源,利用无需授权的自由光谱实现无线连接的新型无线通信技术,支持高密度…...
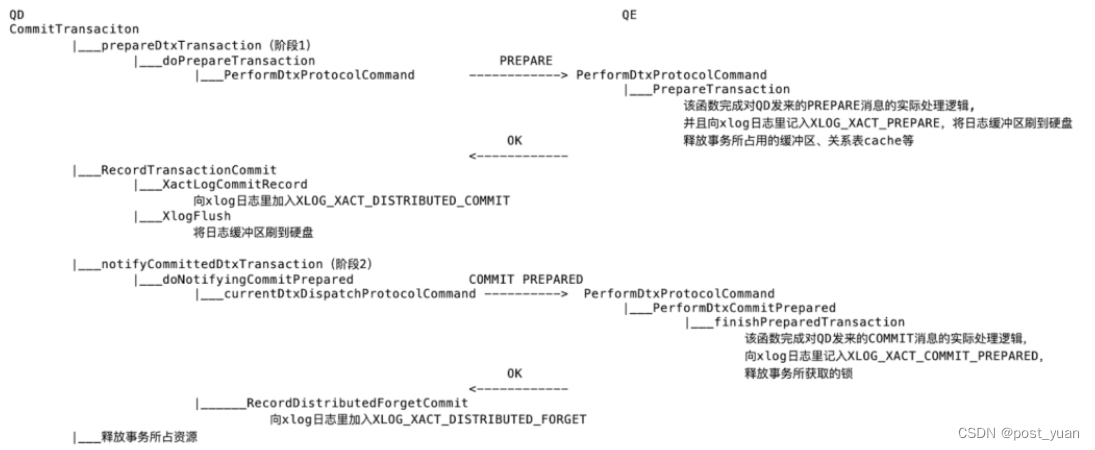
Greenplum的两阶段提交
注:本文章引自终于把分布式事务讲明白了! 在前面的文章中,我们了解了单机库中的事务一致性实现以及分布式事务中的两阶段提交协议。大多数分布式系统都是采用了两阶段提交塄来保证事务的原子性,Greenplum也是采用了两阶段提交&am…...
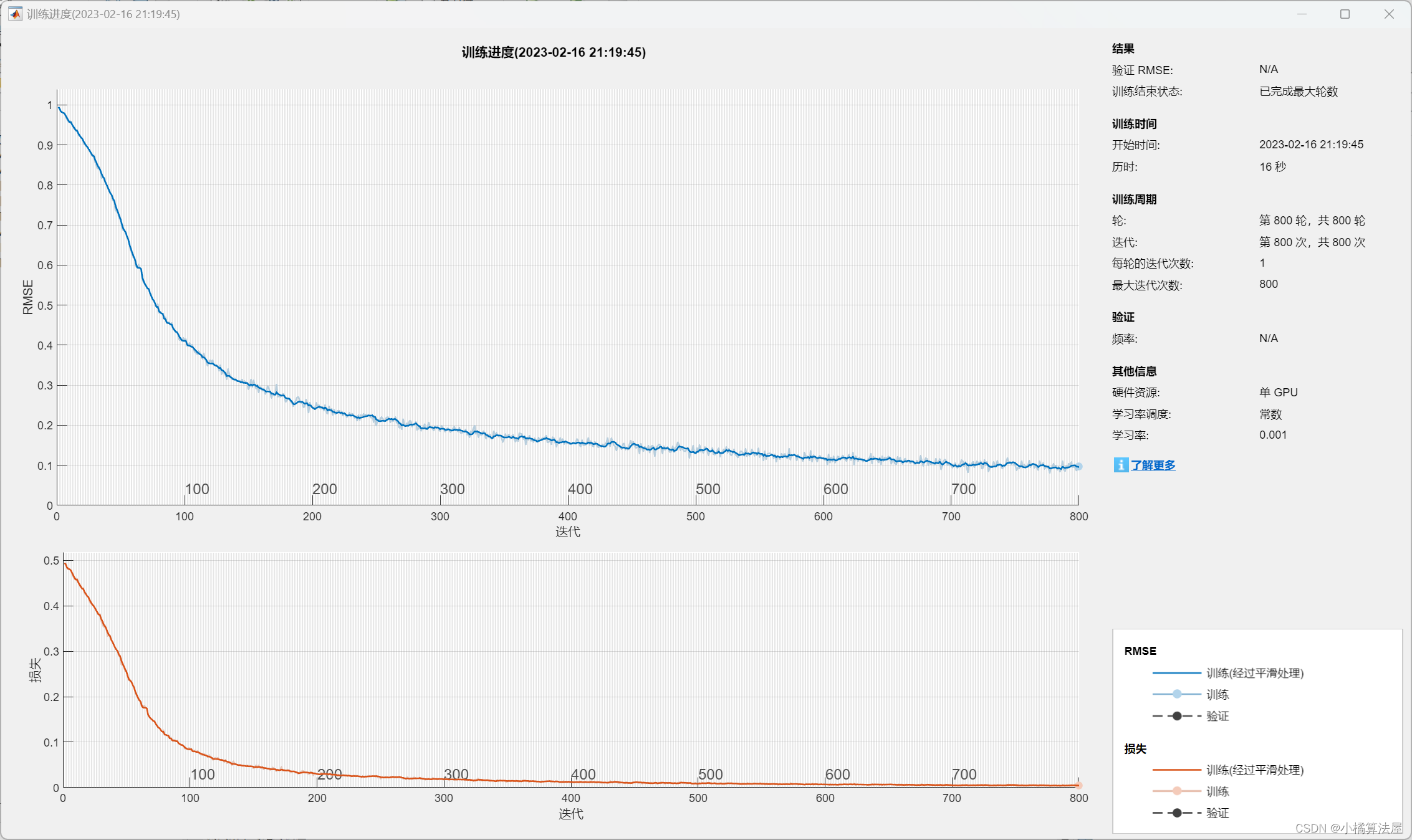
多元回归分析 | CNN-BiLSTM卷积双向长短期记忆神经网络多输入单输出预测(Matlab完整程序)
多元回归分析 | CNN-BiLSTM卷积双向长短期记忆神经网络多输入单输出预测(Matlab完整程序) 目录 多元回归分析 | CNN-BiLSTM卷积双向长短期记忆神经网络多输入单输出预测(Matlab完整程序)预测结果评价指标基本介绍程序设计参考资料预测结果 评价指标 训练结束: 已完成最大轮…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
