红黑树深入剖析【C++】
目录
一、红黑树概念
二、红黑树节点结构设计
三、插入操作
处理情况1
处理情况2
处理情况3
插入总结:
四、插入操作源码
五、红黑树验证
一、红黑树概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍(由规则二三四来保证),因而是接近平衡的。因为最长路径为一黑一红,最短路径为全黑。
红黑树还必须满足以下规则:
1. 每个结点不是红色就是黑色(非红即黑)
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的(没有连续的红色)
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点(每条路径上黑色节点的数量相等)(从这一规则也可以得出,在插入一新节点时,该节点必须为红,才会满足该条件)
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点
规则四演示:
二、红黑树节点结构设计
因为红黑树节点非红即黑,所以可以用枚举的思想来例举红节点和黑节点。因为在插入的过程中,可能会存在翻转的情况,所以就需要一个节点的父节点_parent,左孩子_left,右孩子_right。
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{ RBTreeNode<K, V>* _left; // 左孩子RBTreeNode<K, V>* _right; // 右孩子RBTreeNode<K, V>* _parent; // 红黑树需要旋转,为了实现简单给出该字段pair<K, V> _kv; //值域Colour _col; //颜色RBTreeNode(const pair<K, V>& kv) //初始化:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv){}
};三、插入操作
根据规则4,可以得出在插入一个新节点的时候,这个节点一定是为红色的(上已证)。在插入红色节点的时候可能还是会造成红红节点的冲突(违反规则3),所以我们还需要进行变色+旋转的处理方法
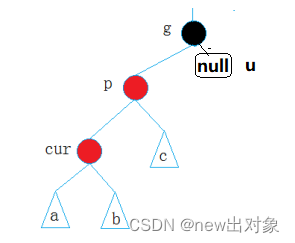
在插入新节点后,因为新节点的默认颜色是红色,因此:如果其父亲节点的颜色是黑色,没有违反红黑树任何规则,则不需要调整;但当新插入节点的父亲节点颜色为红色时,就违反了规则3不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:为方便我们进行变色和旋转的处理,我们定义父亲节点为p,叔叔节点为u,祖父节点为g,当前节点为cur(新增)。实际上,根据红黑树的规则,我们可以确定要发生变色或旋转操作时,cur、p、g节点一定是红、红、黑,如果不满足这种情况,那么肯定这颗红黑树在次之前就违背的红黑树的规则。所以变化操作主要取决于叔叔节点u的颜色。如下抽象图表示,s/b/c/de代表的是满足规则的子树。
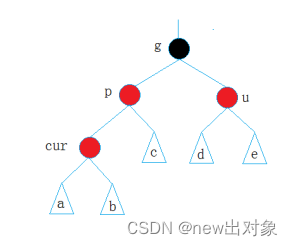
处理情况1
cur为红,p为红,g为黑,u存在且为红
处理方法:叔叔u和父亲p变黑,祖父g变红,再往上进行处理,如果g是根节点,需要把g再变黑,因为根节点必须是黑(规则2)。再往上处理的过程中因为会存在当前g的父节点为红的情况,又再次冲突,所以要进行处理.
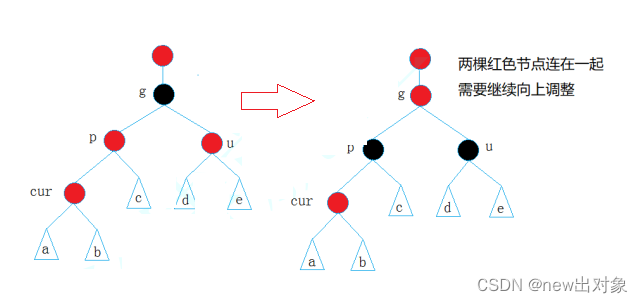
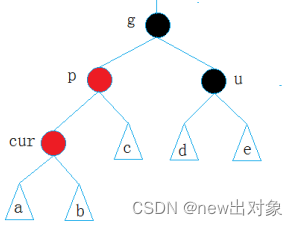
处理情况2
cur为红且在外侧,p为红,g为黑,u不存在/u存在且为黑
u的两种情况:
1.如果u节点不存在,则cur一定是新插入节点,因为如果cur不是新插入节点,则cur和p一定有一个节点的颜色是黑色,就不满足性质4:每条路径黑色节点个数相同。
⒉.如果u节点存在,则其一定是黑色的,那么cur节点原来的颜色一定是黑色的,现在看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由黑色改成红色。
处理方法:单旋+变色。按p节点进行右旋,此时p为红,g为黑,再将p和g的颜色进行交换,即满足红黑树规则。(若p为g的右孩子,cur为p的右孩子,则进行左单旋转,p、g变色--p变黑,g变红)。处理完成后不需要再进行往上处理,因为此时p为黑,p的父亲节点为黑或红都不会对树产生影响。
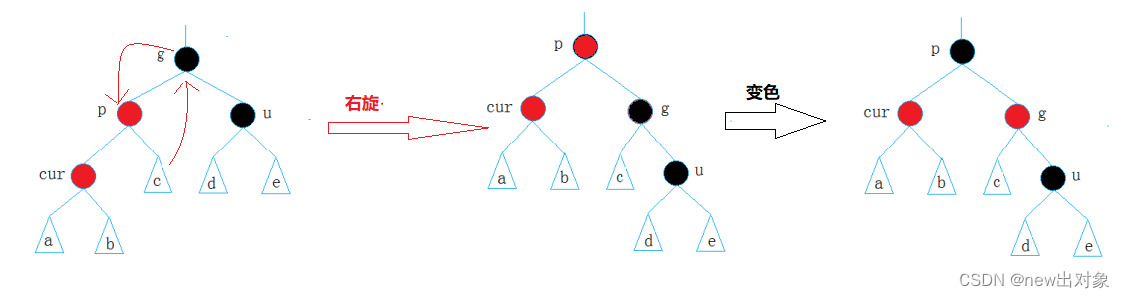
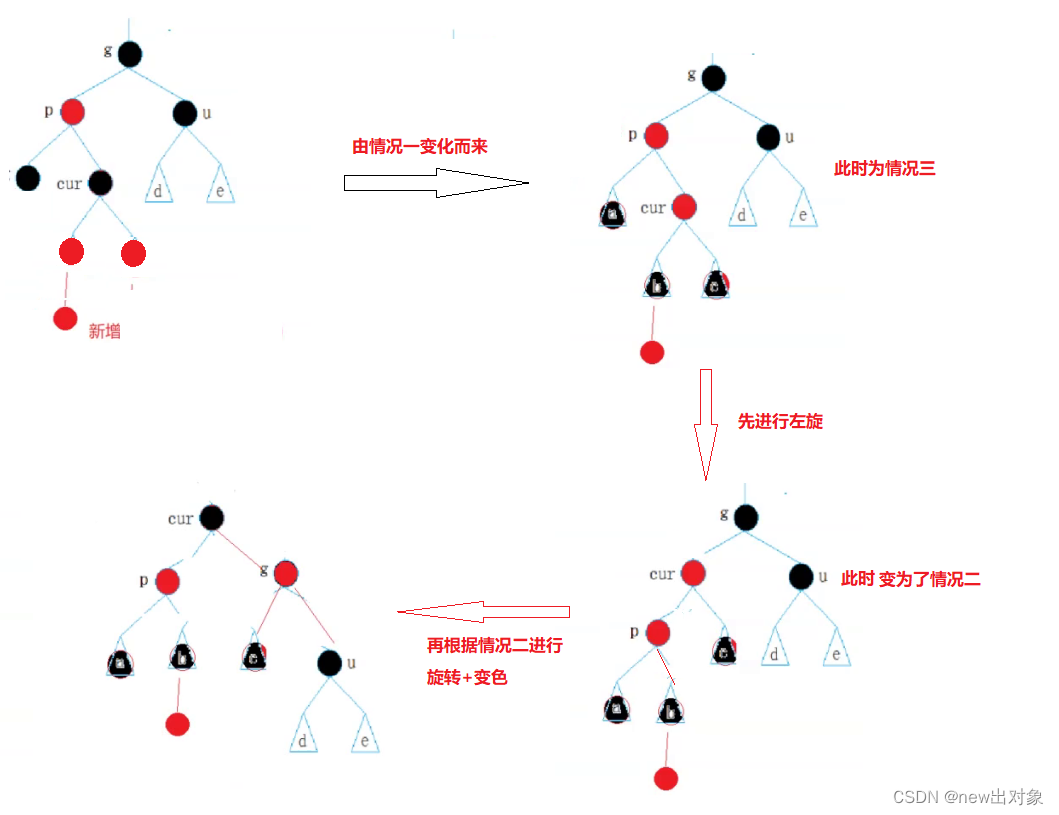
处理情况3
cur为红且在内侧,p为红,g为黑,u不存在/u存在且为黑
处理方法:双旋+变色
u不存在情况:
若p在g的左侧,cur在内侧,则先对g的左子树进行左旋,在对g这棵子树进行右旋;反之,p在g的右侧,cur在内存,就先右旋再左旋再交换cur和g的颜色。
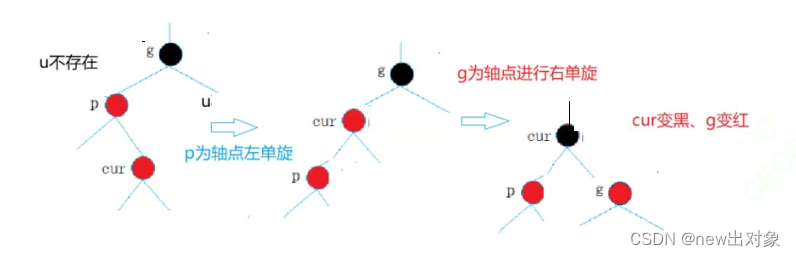
u存在情况:
像这种情况,都是由情况一经过处理后得来的,此时就需要先对g的左子树进行左单旋,旋转后,就会变为情况二,此时再根据情况二的解决方法进行解决,右旋+变色,旋转后将cur和g的颜色进行交换即可。(如果最开始p是在右子树,则操作相反,先右旋再左旋变色。)
插入总结:
1.红黑树插入的节点一定为红色
2.处理三种可能的情况关键在于叔叔节点u
3.u存在且为红(情况一),将p和u节点变黑,g节点变红,若g为根节点就将g变为黑色
4.情况二和情况三都是由情况一经过变化后得来的
4.u不存在或存在且为黑,插入的节点cur在p的外侧(情况二),若p是左子树就进行右旋+交换p、g颜色;若p是右子树,反之,左旋+交换颜色。
5.u不存在或存在且为黑,插入节点cur在p的内侧(情况三),若p是左子树就先进行左旋变为情况二,再进行右旋+交换颜色。反之p为右子树,先进行右旋变为情况二,在进行左旋+交换颜色。
四、插入操作源码
插入源码:
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED) // parent为红色就需要变色处理,因为插入的节点为红{Node* grandfater = parent->_parent; //祖父节点assert(grandfater);assert(grandfater->_col == BLACK);// 关键看叔叔if (parent == grandfater->_left){Node* uncle = grandfater->_right; //叔叔节点// 情况一 : uncle存在且为红,变色+继续往上处理if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;// 继续往上处理cur = grandfater; // 往上处理的时候把祖父当做插入的节点即curparent = cur->_parent;}// 情况二+三:uncle不存在 + 存在且为黑else{// 情况二:右单旋+变色// g // p u// cif (cur == parent->_left){RotateR(grandfater);parent->_col = BLACK;grandfater->_col = RED;}else{// 情况三:左右单旋+变色// g // p u// cRotateL(parent);RotateR(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}else // (parent == grandfater->_right){Node* uncle = grandfater->_left;// 情况一if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;// 继续往上处理cur = grandfater;parent = cur->_parent;}else{// 情况二:左单旋+变色// g // u p// cif (cur == parent->_right){RotateL(grandfater);parent->_col = BLACK;grandfater->_col = RED;}else{// 情况三:右左单旋+变色// g // u p// cRotateR(parent);RotateL(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}}_root->_col = BLACK;return true;}
旋转操作的源码解析可以参考这篇博文:http://t.csdn.cn/iyMac
左旋:
void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}
右旋:
void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}
五、红黑树验证
验证方法:判断从根节点起的每一条子路径中的黑节点数是否相等(规则4)。利用递归的思想遍历每一条路径。再遍历第一条路径的时候,设置一个benchmark记录黑色节点数量,因为规则4,所以后面每一条路径的黑节点数应该都要与之相等,如果不等则不是红黑树。再遍历每一条路径的同时,也可以寻找是否存在连续的红节点(规则三),存在则不满足为红黑树。依次递归每一条路径。
源码:
bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col == RED){cout << "根节点不是黑色" << endl;return false;}// 黑色节点数量基准值int benchmark = 0;return PrevCheck(_root, 0, benchmark);}bool PrevCheck(Node* root, int blackNum, int& benchmark){if (root == nullptr){if (benchmark == 0) // 遍历第一条路径的时候,记录他的黑节点数,后面每一条路径的黑节点数一个都和他相等{benchmark = blackNum;return true;}if (blackNum != benchmark){cout << "某条黑色节点的数量不相等" << endl;return false;}else{return true;}}if (root->_col == BLACK){++blackNum;}if (root->_col == RED && root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}return PrevCheck(root->_left, blackNum, benchmark)&& PrevCheck(root->_right, blackNum, benchmark);}void TestRBTree()
{size_t N = 1000;srand(time(0));RBTree<int, int> t1;for (size_t i = 0; i < N; ++i){int x = rand();cout << "Insert:" << x << ":" << i << endl;t1.Insert(make_pair(x, i));}cout << "IsBalance:" << t1.IsBalance() << endl; //打印1则是红黑树,否则不是
}相关文章:

红黑树深入剖析【C++】
目录 一、红黑树概念 二、红黑树节点结构设计 三、插入操作 处理情况1 处理情况2 处理情况3 插入总结: 四、插入操作源码 五、红黑树验证 一、红黑树概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色࿰…...
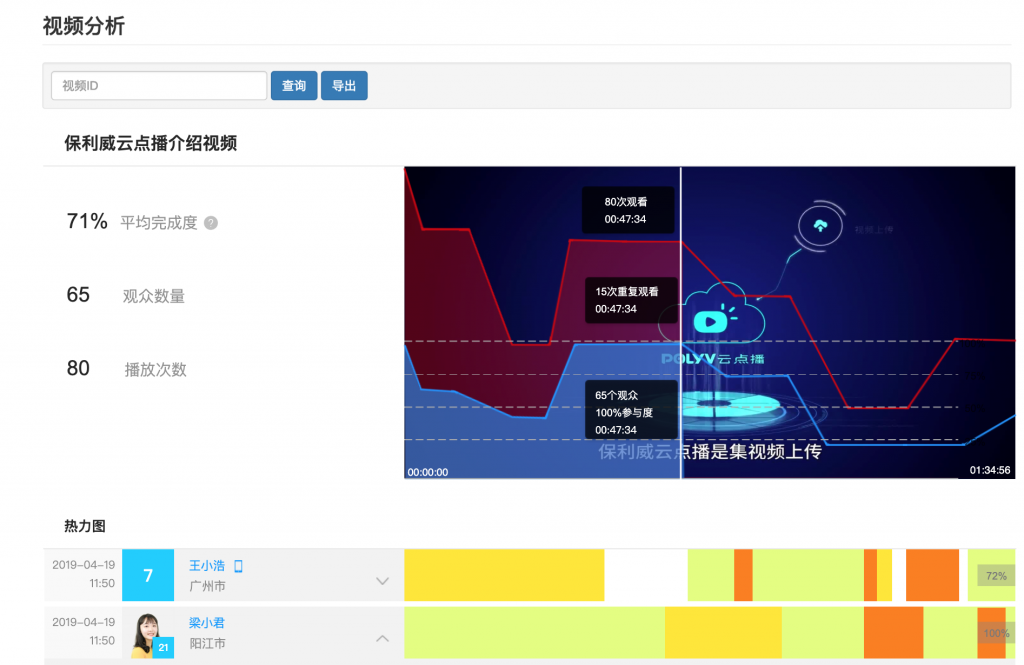
教育机构视频播放时观看行为分析有哪些应用?
教育机构视频播放时观看行为分析有哪些应用? 观看行为分析 观看行为分析是指我们平台基于视频大数据分析,能够以秒为粒度展示观众如何观看您的视频。 视频观看热力图是单次观看行为的图形化表示,我们平台云点播视频的每一次播放࿰…...

Jmeter+验证json结果是否正确小技巧
前言: 通过sql语句或者返回的参数,可以在查看结果树返回的结果中,用方法先跑一下验证是否取到自己想要的值 步骤: 1、添加查看结果树 2、跑出结果 3、在查看结果树中 text改成选Json Path Tester 返回的值如果是列表里面的字符…...
: singleton类型的bean和prototype类型的bean协同工作的方法(一))
Spring 6.0官方文档示例(22): singleton类型的bean和prototype类型的bean协同工作的方法(一)
一、配置文件: <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xmlns:context"http://www.springframework.org/schema/context"xsi:schemaLocation"http…...

Android平台GB28181设备接入侧如何同时对外输出RTSP流?
技术背景 GB28181的应用场景非常广泛,如公共安全、交通管理、企业安全、教育、医疗等众多领域,细分场景可用于如执法记录仪、智能安全帽、智能监控、智慧零售、智慧教育、远程办公、明厨亮灶、智慧交通、智慧工地、雪亮工程、平安乡村、生产运输、车载终…...
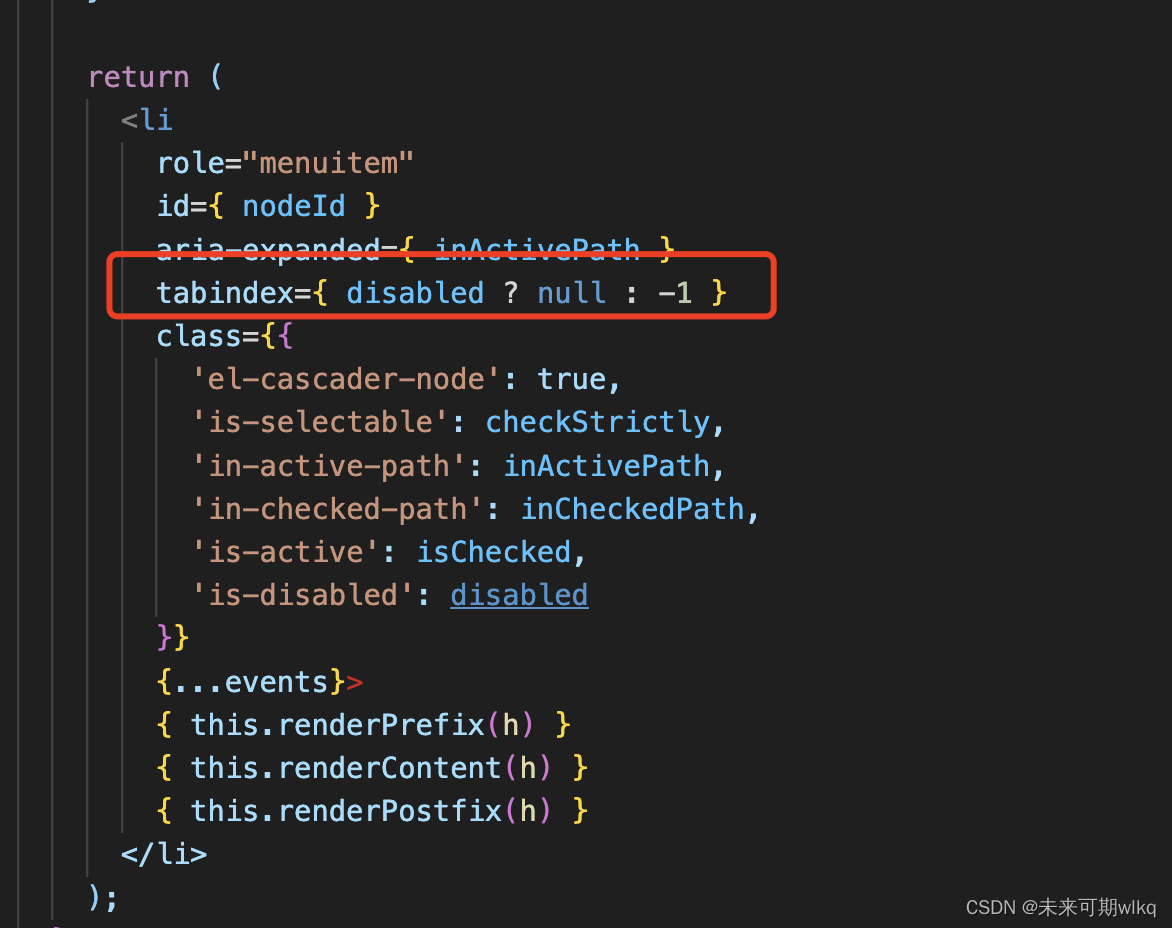
el-Cascader 中div上绑定keyDown事件
keydown,keyup,keypress 事件默认是给页面上可以聚焦的元素绑定键盘事件,例如input输入框,点击输入框即代表聚焦在该元素上。那么想要给div或者其他不能聚焦的元素上使用键盘事件怎么处理呢?这里用到tabindex属性。 …...

elementUI 表格滚动分页加载请求数据
需求:elementui Table表格滚动分页(不使用分页组件),请求数据。 1、自定义加载更多数据的指令,在utils文件夹中创建 loadMore.js /*** 加载更多数据的指令*/ export default {install(Vue) {Vue.mixin({directives: …...

JAVA面试总结-Redis篇章(五)——持久化
Java面试总结-Redis篇章(五)——持久化 1.RDBRDB全称Redis Database Backup file (Redis数据备份文件),也被叫做Redis数据快照。简单来说就是把内存中的所有数据都记录到磁盘中。当Redis实例故障重启后,从磁盘读取快照文件&#x…...
【数据结构】·顺序表函数实现·赶紧学起来呀
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
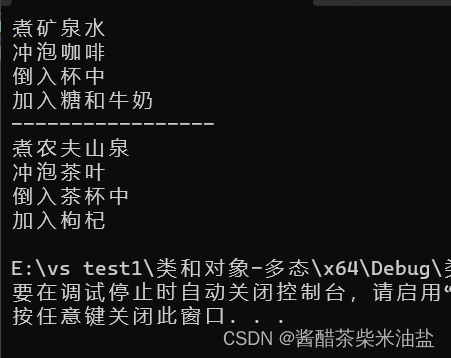
C++,类和对象-多态,制作饮品
#include<iostream> using namespace std;//多态案例,制作饮品class AbstractDrinking { public://煮水virtual void Boil() 0;//冲泡virtual void Brew() 0;//倒入茶杯virtual void PourInCup() 0;//加入辅料virtual void PutSomething() 0;//制作饮品vo…...

网站分析:学习如何分析目标网站的页面结构和URL规律,确定爬取目标和策略。
要学习如何分析目标网站的页面结构和URL规律,确定爬取目标和策略,可以遵循以下步骤: 目标网站的页面结构分析: 寻找目标网站的主页,并观察主页上的链接、导航菜单和内容分类等元素,以了解网站的整体结构。 …...

《向量数据库指南》:向量数据库Pinecone如何集成数据湖
目录 为什么选择Databricks? 为什么选择Pinecone? 设置Spark集群 环境设置 将数据集加载到分区中 创建将文本转换为嵌入的函数 将UDF应用于数据 更新嵌入 摘要 使用Databricks和Pinecone在规模上创建和索引向量嵌入 建立在Apache Spark之上的Databricks是一个强大的…...

Vue3中使用pinia
在Vue 3中使用Pinia,您需要按照以下步骤进行设置: 安装Pinia: npm install pinia创建和配置Pinia存储: // main.jsimport { createApp } from vue import { createPinia } from pinia import App from ./App.vueconst app create…...
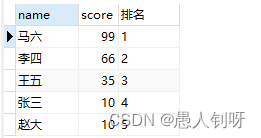
Mysql中(@i:=@i+1)的介绍
i:i1 表达式 生成伪列实现自增序列 语法: select (i:i1) as ,t.* from table_name t,(select i:0) as j (i:i1)代表定义一个变量,每次叠加 1; (select i:0) as j 代表建立一个临时表,j是随便取的表名,但别名一定…...

Nexperia和KYOCERA AVX Components Salzburg 就车规氮化镓功率模块达成合作
Nexperia和KYOCERA AVX Components Salzburg 就车规氮化镓功率模块达成合作 基础半导体器件领域的高产能生产专家Nexperia(安世半导体)近日宣布与国际著名的为汽车行业提供先进电子器件的供应商 KYOCERA AVX Components (Salzburg) GmbH 建立合作关系&am…...
数据库应用:Redis安装部署
目录 一、理论 1.缓存 2.关系型数据库与非关系型数据库 3.Redis 4.Redis安装部署 5.Redis命令工具 6.Redis数据库常用命令 7.Redis多数据库操作 二、实验 1.Redis安装部署 2.Redis命令工具 3.Redis数据库命令 4.Redis多数据库操作 三、问题 1.RESP连接CentOS 7 R…...
7.Docker-compose
文章目录 Docker-compose概念Docker-compose部署YAML文件格式和编写注意事项注意数据结构对象映射序列属组布尔值序列的映射映射的映射JSON格式文本换行锚点和引用 Docker compose配置常用字段docker compose常用命令Docker Compose 文件结构docker compose部署apachedocker co…...

多线程:管程法
管程法 生产者把生产好的数据放入缓冲区,消费者从缓冲区拿出数据 package jingcheng.test.gaoji; //测试生产者消费者模型-->利用缓冲区解决:管程法 //生产者,消费者,产品,缓冲区 public class TestPc {public st…...

7.1 String StringBuffer 和 StringBuilder 的区别是什么? String 为什么是不可变的?
可变性 简单的来说:String 类中使用 final 关键字修饰字符数组来保存字符串,private final char value[],所以String 对象是不可变的。 补充(来自issue 675):在 Java 9 之后,String 、StringBu…...

【C++STL标准库】容器适配器
功能:将功能类似,但是接口不符合的接口转换成另一个接口 stack 栈stack(栈) 特点:先入后出,只能从栈顶弹出值,只能从栈顶压入值 也就是说栈需要的功能:push_back、pop_back 所以可…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...