基于杜鹃鸟鲶鱼优化(Cuckoo Catfish Optimizer,CCO)算法的多个无人机协同路径规划(可以自定义无人机数量及起始点),MATLAB代码
一、杜鹃鸟鲶鱼优化算法
杜鹃鸟鲶鱼优化(Cuckoo Catfish Optimizer,CCO)算法模拟了杜鹃鸟鲶鱼的搜索、捕食和寄生慈鲷行为。该算法的早期迭代侧重于执行多维包络搜索策略和压缩空间策略,并结合辅助搜索策略来有效限制慈鳔的逃逸空间。此阶段确保对解决方案空间进行广泛探索。在迭代的中间阶段,该算法采用过渡策略促进从勘探到开发的平滑过渡,赋予了算法一定的勘探能力和开发能力。在后期阶段,该算法使用混沌捕食机制在慈鳷周围制造干扰,以提高对最优解的利用。在整个优化过程中,整合了个体的引导、寄生和死亡机制,让个体能够实时调整位置,提高整体收敛精度。

参考文献
[1]Tian-Lei Wang, Shao-Wei Gu, Ren-Ju Liu, Le-Qing Chen, Zhu Wang*, Zhi-Qiang Zeng*. Cuckoo Catfish Optimizer: A New Meta-Heuristic Optimization Algorithm. Artificial Intelligence Review,2024
二. 无人机路径规划数学模型
2.1 路径最优性
为了提高无人机的操作效率,规划的路径需要在特定的应用标准下达到最优。在我们的研究中,主要关注空中摄影、测绘和表面检查,因此选择最小化路径长度作为优化目标。由于无人机通过地面控制站(GCS)进行控制,飞行路径 X i X_i Xi 被表示为无人机需要飞越的一系列 n n n 个航路点的列表。每个航路点对应于搜索地图中的一个路径节点,其坐标为 P i j = ( x i j , y i j , z i j ) P_{ij} = (x_{ij}, y_{ij}, z_{ij}) Pij=(xij,yij,zij)。通过表示两个节点之间的欧几里得距离为 $| \overrightarrow{P_{ij}P_{i,j+1}} |,与路径长度相关的成本 F 1 F_1 F1 可以计算为:
F 1 ( X ) = ∑ j = 1 n − 1 ∥ P i j P i , j + 1 → ∥ F_1(X) = \sum_{j=1}^{n-1} \| \overrightarrow{P_{ij}P_{i,j+1}} \| F1(X)=j=1∑n−1∥PijPi,j+1∥
2.2 安全性和可行性约束
除了最优性之外,规划的路径还需要确保无人机的安全操作,引导其避开操作空间中可能出现的威胁,这些威胁通常由障碍物引起。设 K K K 为所有威胁的集合,每个威胁被假设为一个圆柱体,其投影的中心坐标为 C k C_k Ck,半径为 R k R_k Rk,如下图 所示。

对于给定的路径段 ∥ P i j P i , j + 1 → ∥ \| \overrightarrow{P_{ij}P_{i,j+1}} \| ∥PijPi,j+1∥,其相关的威胁成本与它到 C k C_k Ck 的距离 d k d_k dk 成正比。考虑到无人机的直径 D D D 和到碰撞区域的危险距离 S S S,威胁成本 F 2 F_2 F2 在障碍物集合 K K K 上计算如下:
F 2 ( X i ) = ∑ j = 1 n − 1 ∑ k = 1 K T k ( P i j P i , j + 1 → ) , F_2(X_i) = \sum_{j=1}^{n-1} \sum_{k=1}^K T_k(\overrightarrow{P_{ij}P_{i,j+1}}), F2(Xi)=j=1∑n−1k=1∑KTk(PijPi,j+1),
其中
T k ( P i j P i , j + 1 → ) = { 0 , if d k > S + D + R k ( S + D + R k ) − d k , if D + R k < d k ≤ S + D + R k ∞ , if d k ≤ D + R k T_k(\overrightarrow{P_{ij}P_{i,j+1}}) = \begin{cases} 0, & \text{if } d_k > S + D + R_k \\ (S + D + R_k) - d_k, & \text{if } D + R_k < d_k \leq S + D + R_k \\ \infty, & \text{if } d_k \leq D + R_k \end{cases} Tk(PijPi,j+1)=⎩ ⎨ ⎧0,(S+D+Rk)−dk,∞,if dk>S+D+Rkif D+Rk<dk≤S+D+Rkif dk≤D+Rk
在操作过程中,飞行高度通常被限制在给定的最小和最大高度之间,例如在调查和搜索应用中,需要相机以特定的分辨率和视场收集视觉数据,从而限制飞行高度。设最小和最大高度分别为 h min h_{\text{min}} hmin 和 h max h_{\text{max}} hmax。与航路点 P i j P_{ij} Pij 相关的高度成本计算为:
H i j = { ∣ h i j − h max + h min 2 ∣ , if h min ≤ h i j ≤ h max ∞ , otherwise H_{ij} = \begin{cases} |h_{ij} - \frac{h_{\text{max}} + h_{\text{min}}}{2}|, & \text{if } h_{\text{min}} \leq h_{ij} \leq h_{\text{max}} \\ \infty, & \text{otherwise} \end{cases} Hij={∣hij−2hmax+hmin∣,∞,if hmin≤hij≤hmaxotherwise
其中 h i j h_{ij} hij 表示相对于地面的飞行高度,如下图所示。

可以看出, H i j H_{ij} Hij 保持平均高度并惩罚超出范围的值。对所有航路点求和得到高度成本:
F 3 ( X ) = ∑ j = 1 n H i j F_3(X) = \sum_{j=1}^n H_{ij} F3(X)=j=1∑nHij
平滑成本评估转弯率和爬升率,这对于生成可行路径至关重要。如下图 所示。

转弯角 ϕ i j \phi_{ij} ϕij 是两个连续路径段 P i j ′ P i , j + 1 ′ → \overrightarrow{P'_{ij}P'_{i,j+1}} Pij′Pi,j+1′ 和 P i , j + 1 ′ P i , j + 2 ′ → \overrightarrow{P'_{i,j+1}P'_{i,j+2}} Pi,j+1′Pi,j+2′ 在水平面 Oxy 上的投影之间的角度。设 k → \overrightarrow{k} k 是 z 轴方向的单位向量,投影向量可以计算为:
P i j ′ P i , j + 1 ′ → = k → × ( P i j P i , j + 1 → × k → ) \overrightarrow{P'_{ij}P'_{i,j+1}} = \overrightarrow{k} \times (\overrightarrow{P_{ij}P_{i,j+1}} \times \overrightarrow{k}) Pij′Pi,j+1′=k×(PijPi,j+1×k)
因此,转弯角计算为:
ϕ i j = arctan ( ∥ P i j ′ P i , j + 1 ′ → × P i , j + 1 ′ P i , j + 2 ′ → ∥ P i j P i , j + 1 ′ → ⋅ P i , j + 1 ′ P i , j + 2 ′ → ) \phi_{ij} = \arctan\left( \frac{\| \overrightarrow{P'_{ij}P'_{i,j+1}} \times \overrightarrow{P'_{i,j+1}P'_{i,j+2}} \|}{\overrightarrow{P_{ij}P'_{i,j+1}} \cdot \overrightarrow{P'_{i,j+1}P'_{i,j+2}}} \right) ϕij=arctan PijPi,j+1′⋅Pi,j+1′Pi,j+2′∥Pij′Pi,j+1′×Pi,j+1′Pi,j+2′∥
爬升角 ψ i j \psi_{ij} ψij 是路径段 P i j P i , j + 1 → \overrightarrow{P_{ij}P_{i,j+1}} PijPi,j+1 与其在水平面上的投影 P i j ′ P i , j + 1 ′ → \overrightarrow{P'_{ij}P'_{i,j+1}} Pij′Pi,j+1′ 之间的角度,由下式给出:
ψ i j = arctan ( z i , j + 1 − z i j ∥ P i j ′ P i , j + 1 ′ → ∥ ) \psi_{ij} = \arctan\left( \frac{z_{i,j+1} - z_{ij}}{\| \overrightarrow{P'_{ij}P'_{i,j+1}} \|} \right) ψij=arctan ∥Pij′Pi,j+1′∥zi,j+1−zij
然后,平滑成本计算为:
F 4 ( X ) = a 1 ∑ j = 1 n − 2 ϕ i j + a 2 ∑ j = 1 n − 1 ∣ ψ i j − ψ j − 1 ∣ F_4(X) = a_1 \sum_{j=1}^{n-2} \phi_{ij} + a_2 \sum_{j=1}^{n-1} |\psi_{ij} - \psi_{j-1}| F4(X)=a1j=1∑n−2ϕij+a2j=1∑n−1∣ψij−ψj−1∣
其中 a 1 a_1 a1 和 a 2 a_2 a2 分别是转弯角和爬升角的惩罚系数。
2.3 总体成本函数
2.3.1 单个无人成本计算
考虑到路径 X X X 的最优性、安全性和可行性约束,第 i i i 个无人机总体成本函数可以定义为以下形式:
f i ( X ) = ∑ k = 1 4 b k F k ( X i ) f_i(X) = \sum_{k=1}^4 b_k F_k(X_i) fi(X)=k=1∑4bkFk(Xi)
其中 b k b_k bk 是权重系数, F 1 ( X i ) F_1(X_i) F1(Xi) 到 F 4 ( X i ) F_4(X_i) F4(Xi) 分别是路径长度、威胁、平滑度和飞行高度相关的成本。决策变量是 X X X,包括 n n n 个航路点 P i j = ( x i j , y i j , z i j ) P_{ij} = (x_{ij}, y_{ij}, z_{ij}) Pij=(xij,yij,zij) 的列表,使得 P i j ∈ O P_{ij} \in O Pij∈O,其中 O O O 是无人机的操作空间。根据这些定义,成本函数 F F F 是完全确定的,可以作为路径规划过程的输入。
2.3.2 多无人机总成本计算
若共有 m m m 个无人机,其总成本为单个无人机成本和,计算公式如下:
f i t n e s s ( X ) = ∑ i = 1 m f i ( X ) fitness(X) = \sum_{i=1}^mf_i(X) fitness(X)=i=1∑mfi(X)
参考文献:
[1] Phung M D , Ha Q P .Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization[J].Applied Soft Computing, 2021(2):107376.DOI:10.1016/j.asoc.2021.107376.
三、部分代码及结果
close all
clear
clc
% dbstop if all error
pop=100;%种群大小(可以修改)
maxgen=200;%最大迭代(可以修改)%% 模型建立
model=Create_Model();
UAVnum=4;%无人机数量(可以修改) 必须与无人机的起始点保持一致%% 初始化每个无人机的模型
for i=1:UAVnumModelUAV(i).model=model;
end%% 第一个无人机 起始点
start_location = [120;200;100];
end_location = [800;800;150];
ModelUAV(1).model.start=start_location;
ModelUAV(1).model.end=end_location;
%% 第二个无人机 起始点
start_location = [400;100;100];
end_location = [900;600;150];
ModelUAV(2).model.start=start_location;
ModelUAV(2).model.end=end_location;
%% 第三个无人机 起始点
start_location = [200;150;150];
end_location =[850;750;150];
ModelUAV(3).model.start=start_location;
ModelUAV(3).model.end=end_location;
%% 第四个无人机 起始点
start_location = [100;100;150];
end_location = [800;730;150];
ModelUAV(4).model.start=start_location;
ModelUAV(4).model.end=end_location;
%% 第5个无人机 起始点
% start_location = [500;100;130];
% end_location = [850;650;150];
% ModelUAV(5).model.start=start_location;
% ModelUAV(5).model.end=end_location;
% %% 第6个无人机 起始点
% start_location = [100;100;150];
% end_location = [800;800;150];
% ModelUAV(6).model.start=start_location;
% ModelUAV(6).model.end=end_location;
五个无人机:





四、完整MATLAB代码见下方名片

相关文章:

基于杜鹃鸟鲶鱼优化(Cuckoo Catfish Optimizer,CCO)算法的多个无人机协同路径规划(可以自定义无人机数量及起始点),MATLAB代码
一、杜鹃鸟鲶鱼优化算法 杜鹃鸟鲶鱼优化(Cuckoo Catfish Optimizer,CCO)算法模拟了杜鹃鸟鲶鱼的搜索、捕食和寄生慈鲷行为。该算法的早期迭代侧重于执行多维包络搜索策略和压缩空间策略,并结合辅助搜索策略来有效限制慈鳔的逃逸空…...

16个气象数据可视化网站整理分享
好的!以下是关于“16个气象数据可视化网站整理分享”的软文: 16个气象数据可视化网站整理分享 气象数据可视化已成为现代气象研究、决策支持以及公众天气服务的重要组成部分。从天气预报到气候变化监测,全球许多气象数据可视化平台为专业人士…...

word光标一直闪的解决办法
在选项里,打开首选项,(如果打不开,可以新建一个word也许就可以,实在不行只能靠眼疾手快,趁他还没闪赶紧点) 选COM加载项,在里面取消勾选MicrosoftOfficePLUS...

⑥ ACG-系统管理
上网管理行为是指对员工在工作时间内使用公司网络的行为进行管理和监督。在企业中,系统管理是实施上网管理行为的重要方式之一。系统管理包括以下几个方面: 1. 访问控制:通过设置网络访问权限,对员工访问特定网站或使用特定应用程…...

基于大模型的肺良性肿瘤术前、术中、术后全流程预测与诊疗方案研究
目录 一、引言 1.1 研究背景与意义 1.2 研究目的 1.3 国内外研究现状 二、大模型预测原理与方法 2.1 大模型概述 2.2 数据收集与预处理 2.3 特征工程 2.4 模型训练与优化 三、术前预测与方案制定 3.1 肿瘤性质预测 3.1.1 预测模型构建 3.1.2 预测结果分析 3.2 手…...

C++ map容器总结
map基本概念 简介: map中所有元素都是pair pair中第一个元素为key(键值),起到索引作用,第二个元素为value(实值) 所有元素都会根据元素的键值自动排序 本质: map/multimap属于关…...

推荐系统(十五):基于双塔模型的多目标商品召回/推荐系统
在电商推荐场景中,用户行为通常呈现漏斗形态:曝光→点击→转化。本文基于TensorFlow构建了一个支持多任务学习的双塔推荐模型,可同时预测点击率(CTR)和转化率(CVR)。通过用户塔和商品塔的分离式设计,模型既能捕捉用户兴趣偏好,又能理解商品特征,最终通过向量相似度计…...

【MLP-BEV(10)】BEVPooling V1和BEVPooling V2的view_transformer,进行鱼眼图片实践
文章目录 先说说 BEVPoolv1步骤1:3D点生成步骤2 2D特征采样和BEV特征生成特点再谈谈BEVPoolv2步骤1:3D点生成步骤2: 计算索引关系步骤3: `voxel_pooling`计算鱼眼图片进行实践步骤1、3D点生成(基于Kannala-Brandt 进行调整)步骤2、2D特征采样和BEV特征生成(1) 体素化 (Voxe…...

Elasticsearch:使用 Azure AI 文档智能解析 PDF 文本和表格数据
作者:来自 Elastic James Williams 了解如何使用 Azure AI 文档智能解析包含文本和表格数据的 PDF 文档。 Azure AI 文档智能是一个强大的工具,用于从 PDF 中提取结构化数据。它可以有效地提取文本和表格数据。提取的数据可以索引到 Elastic Cloud Serve…...
)
常考计算机操作系统面试习题(四)
目录 1. Peterson 算法伪代码 2. 信号量生产者消费者问题分析 3. 注释 Peterson 主函数并分析输出结果 4. 用 fork 创建子进程的程序 1. Peterson 算法伪代码 题目: 写出 Peterson 算法的伪代码。 参考答案: // 定义变量 boolean flag[2]; /…...

IP 分片重组与 TCP 会话重组
1. IP 分片重组(IP Fragmentation & Reassembly) (1)分片原因 当 IP 数据包长度超过 MTU(Maximum Transmission Unit)(如以太网默认 1500 字节)时,路由器或发送端会…...
【 <二> 丹方改良:Spring 时代的 JavaWeb】之 Spring Boot 中的 AOP:实现日志记录与性能监控
<前文回顾> 点击此处查看 合集 https://blog.csdn.net/foyodesigner/category_12907601.html?fromshareblogcolumn&sharetypeblogcolumn&sharerId12907601&sharereferPC&sharesourceFoyoDesigner&sharefromfrom_link <今日更新> 一、开篇整…...

多模态大模型训练范式演进与前瞻
本文从多模态大模型相关概念出发,并以Flamingo 模型为例,探讨了基于多模态大模型训练的演进与前瞻。新一代训练范式包括统一架构、数据工程革新和动态适应机制,以提升跨模态推理能力和长视频理解。 多模态大模型 定义 什么是多模态大模型&…...

游戏引擎学习第187天
看起来观众解决了上次的bug 昨天遇到了一个相对困难的bug,可以说它相当棘手。刚开始的时候,没有立刻想到什么合适的解决办法,所以今天得从头开始,逐步验证之前的假设,收集足够的信息,逐一排查可能的原因&a…...

HarmonyOS NEXT 关于鸿蒙的一多开发(一次开发,多端部署) 1+8+N
官方定义 定义:一套代码工程,一次开发上架,多端按需部署。 目标:支撑开发者快速高效的开发支持多种终端设备形态的应用,实现对不同设备兼容的同时,提供跨设备的流转、迁移和协同的分布式体验。 什么是18…...

SAP-ABAP:OData 协议深度解析:架构、实践与最佳应用
OData 协议深度解析:架构、实践与最佳应用 一、协议基础与核心特性 协议定义与目标 定位:基于REST的开放数据协议,标准化数据访问接口,由OASIS组织维护,最新版本为OData v4.01。设计哲学:通过统一资源标识符(URI)和HTTP方法抽象数据操作,降低异构系统集成复杂度。核心…...

当Kafka化身抽水马桶:论组件并发提升与系统可用性的量子纠缠关系
《当Kafka化身抽水马桶:论组件并发提升与系统可用性的量子纠缠关系》 引言:一场OOM引发的血案 某个月黑风高的夜晚,监控系统突然发出刺耳的警报——我们的数据发现流水线集体扑街。事后复盘发现:Kafka集群、Gateway、Discovery服…...

Dify+ollama+vanna 实现text2sql 智能数据分析 -01
新鲜出炉-今天安装vanna踩过的坑 今天的任务是安装vanna这个工具,因为dify中自己写的查询向量数据库和执行sql这两步太慢了大概要20S,所以想用下这个工具,看是否会快一点。后面会把这个vanna封装成一个工具让dify调用。 环境说明 我是在本…...

【Python实用技巧】OS模块详解:文件与目录操作的瑞士军刀
大家好,我是唐叔!今天咱们来聊聊Python中那个被低估的"老黄牛"——os模块。这个模块看似简单,但却是每个Python开发者都绕不开的利器。就像我常说的:“不会用os模块的Python程序员,就像不会用筷子的美食家”…...

动态内存分配与内存对齐
在C语言及其他低级编程语言中,内存管理是一个至关重要的主题。动态内存分配和内存对齐是确保程序高效和稳定运行的关键因素。本文将深入探讨动态内存分配的原理,内存对齐的概念,并解释它们如何共同影响程序的性能和资源利用。 一、动态内存分配简介 1.1 动态内存分配的概念…...

C 标准库 – 头文件
1️⃣ <fenv.h> 简介 <fenv.h> 提供了用于控制和检查浮点运算行为的宏和函数。它为浮点环境提供了精细的控制,允许设置舍入模式、捕获浮点异常等。通过 <fenv.h>,程序员可以: 控制浮点舍入模式,指定不同的舍入…...

Redis的基础,经典,高级问题解答篇
目录 一,基础 二,经典 缓存雪崩: 1. Redis事务的原子性 2. 与MySQL事务的区别 1. 主从复制原理 2. 哨兵模式故障转移流程 3. 客户端感知故障转移 三,高级 一,基础 Redis的5种基础数据类型及使用场景…...

uniapp uni-swipe-action滑动内容排版改造
在uniapp开发中 默认的uni-swipe-action滑动组件 按钮里的文字都是横排的 不能换行的 如果是在一些小屏设备 比如PDA这种,同时按钮文字又都是4个字 多按钮的情况 就会发现滑动一下都直接满屏了 观看体验都不好 但默认的官方组件又没有样式的设置,下面就告…...

电脑卡怎么办?提升电脑流畅的方法
电脑已经成为我们工作、学习和娱乐不可或缺的伙伴。然而,随着使用时间的增长,许多用户会遇到电脑运行变慢、卡顿的情况,这不仅影响了工作效率,也大大降低了使用体验。本文将为大家分析电脑卡顿的常见原因,并提供一套实…...

SpringBoot报错解决方案
org.apache.tomcat.util.http.fileupload.impl.SizeLimitExceededException: the request was rejected because its size (31297934) exceeds the configured maximum (10485760) 文件上传大小超过限制...
)
知识表示方法之二:产生式表示法(Production System)
有关知识表示方法之一:一阶谓词逻辑的内容可以看我的文章:https://blog.csdn.net/lzm12278828/article/details/146541478 一、定义 “产生式”这一术语是有美国数学家博斯特(E.Post)在1943年首先提出来的,他根据串替代规则提出了一种称为波斯特机的计算模型,模型中的每…...

SQL Server中账号权限
目录标题 查看现有权限授予权限拒绝权限撤销权限角色管理 在SQL Server中管理账号权限主要通过以下几个关键步骤: 查看现有权限 可以使用系统视图来查看账号的权限,比如 sys.database_permissions 视图,示例查询如下: SELECT d…...

软件需求未明确非功能性指标(如并发量)的后果
软件需求未明确非功能性指标(如并发量)可能带来的严重后果包括:系统性能下降、用户体验恶化、稳定性降低、安全风险增加、后期维护成本高企。其中,系统性能下降尤为显著。当软件系统在设计和开发阶段未明确并发量需求时࿰…...

VScode-i18n-ally-Vue
参考这篇文章,做Vue项目的国际化配置,本篇文章主要解释,下载了i18n之后,该如何对Vscode进行配置 https://juejin.cn/post/7271964525998309428 i18n Ally全局配置项 Vscode中安装i18n Ally插件,并设置其配置项&#…...
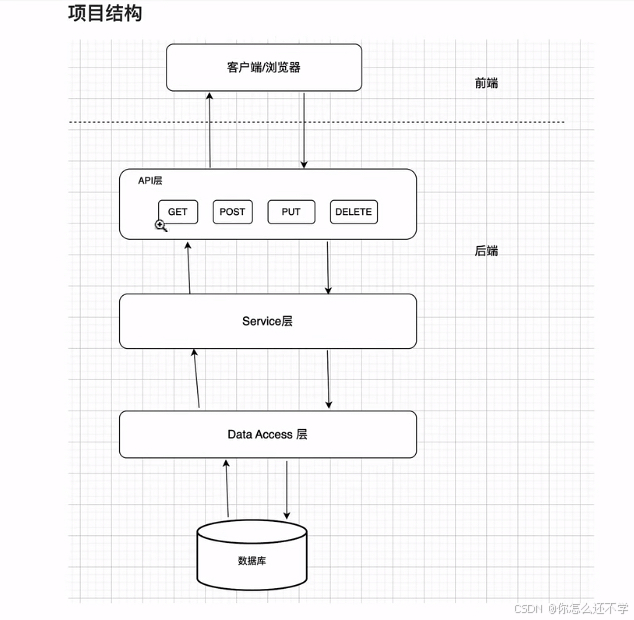
Spring Boot项目快速创建-开发流程(笔记)
主要流程: 前端发送网络请求->controller->调用service->操纵mapper->操作数据库->对entity数据对象赋值->返回前端 前期准备: maven、mysql下载好 跟学视频,感谢老师: https://www.bilibili.com/video/BV1gm4…...
