算法每日一练 (23)
💢欢迎来到张翊尘的技术站
💥技术如江河,汇聚众志成。代码似星辰,照亮行征程。开源精神长,传承永不忘。携手共前行,未来更辉煌💥
文章目录
- 算法每日一练 (23)
- 最大正方形
- 题目描述
- 解题思路
- 解题代码
- `c/c++`
- `golang`
- `lua`
官方站点: 力扣 Leetcode
算法每日一练 (23)
最大正方形
题目地址:最大正方形
题目描述
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:

输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2:

输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300matrix[i][j]为'0'或'1'
解题思路
-
首先创建辅助变量:
m、n、maxVal、dp:m和n分别表示矩阵的行数和列数。maxVal用于记录矩阵中最大的正方形边长,初始值为 0。dp用于记录当前行的正方形边长。
-
紧接着,遍历矩阵的第一行,更新
maxVal和dp[i]的值。这是因为第一行中的每个'1'都可以构成一个边长为 1 的正方形。 -
从第二行开始,遍历矩阵的每个位置
(i, j),对于每一行的每个元素:- 如果是第一列(
j == 0),直接将当前元素的值赋给dp[j]即可。 - 否则,根据动态规划的逻辑更新
dp[j]:- 如果当前元素是
'0',则dp[j]为0,因为无法形成正方形。 - 如果当前元素是
'1',则dp[j]的值为:当前元素的上方(up)、左方(left)和左上方(lup)三个值的最小值加1。这是因为正方形的形成需要依赖于其上方、左方和左上方的正方形边长。
- 如果当前元素是
- 如果是第一列(
-
更新
maxVal为当前列的最大值。 -
最终返回
maxVal的平方,即是满足题意的返回值。
解题代码
c/c++
#include <vector>class Solution
{
public:int maximalSquare(std::vector<std::vector<char>> &matrix){int m = matrix.size();int n = matrix[0].size();int maxVal = 0;std::vector<int> dp(n, 0);for (int i = 0; i < n; i++){dp[i] = matrix[0][i] - '0';maxVal = std::max(maxVal, dp[i]);}for (int i = 1; i < m; i++){int prev = dp[0];for (int j = 0; j < n; j++){int cur = matrix[i][j] - '0';if (j == 0)dp[j] = cur;else{int t = dp[j];if (matrix[i][j] == '0')dp[j] = 0;else{int up = t;int left = dp[j - 1];int lup = prev;dp[j] = std::min(std::min(up, left), lup) + 1;}prev = t;}maxVal = std::max(maxVal, dp[j]);}}return maxVal * maxVal;}
};
golang
func maximalSquare(matrix [][]byte) int {m := len(matrix)n := len(matrix[0])maxVal := 0dp := make([]int, n)for i := 0; i < n; i++ {dp[i] = int(matrix[0][i] - '0')maxVal = max(maxVal, dp[i])}for i := 1; i < m; i++ {prev := dp[0]for j := 0; j < n; j++ {cur := int(matrix[i][j] - '0')if j == 0 {dp[j] = cur} else {t := dp[j]if matrix[i][j] == '0' {dp[j] = 0} else {up, left, lup := t, dp[j-1], prevdp[j] = min(up, left, lup) + 1}prev = t}maxVal = max(maxVal, dp[j])}}return maxVal * maxVal
}
lua
local function maximalSquare(matrix)local m, n = #matrix, #matrix[1]local maxVal = 0local dp = {}for i = 1, n dodp[i] = matrix[1][i] - '0'maxVal = math.max(maxVal, dp[i])endfor i = 2, m dolocal prev = dp[1]for j = 1, n dolocal cur = matrix[i][j] - '0'if j == 1 thendp[j] = curelselocal t = dp[j]if matrix[i][j] == '0' thendp[j] = 0elselocal up, left, lup = t, dp[j - 1], prevdp[j] = math.min(up, left, lup) + 1endprev = tendmaxVal = math.max(maxVal, dp[j])endendreturn maxVal * maxVal
end
🌺🌺🌺撒花!
如果本文对你有帮助,就点关注或者留个👍
如果您有任何技术问题或者需要更多其他的内容,请随时向我提问。

相关文章:

算法每日一练 (23)
💢欢迎来到张翊尘的技术站 💥技术如江河,汇聚众志成。代码似星辰,照亮行征程。开源精神长,传承永不忘。携手共前行,未来更辉煌💥 文章目录 算法每日一练 (23)最大正方形题目描述解题思路解题代码…...

UE5学习笔记 FPS游戏制作28 显式玩家子弹数
文章目录 添加变量修改ShootOnce方法,设计时减少子弹,没有子弹不能开枪在UI上显示 添加变量 在Gun类中添加BulletNum和ClipSize两个参数 BulletNum是当前还有多少子弹,ClipSize是一个弹匣多少子弹 Rifle的ClipSzie设置为30,Laun…...

2025前端八股文终极指南:从高频考点到降维打击的面试突围战
2025前端八股文终极指南:从高频考点到降维打击的面试突围战 一、2025前端八股文核心考点重构 1.1 新型响应式系统三连问 Vue3信号式响应性: // 信号式响应性底层实现 const [count, setCount] createSignal(0) effect(() > {console.log("当…...

《深入探索 Python 数据分析:用 Pandas 高效处理与可视化大型数据集》
《深入探索 Python 数据分析:用 Pandas 高效处理与可视化大型数据集》 引言:从零到分析高手 数据是当代社会最宝贵的资源,而数据分析技能是现代职业人不可或缺的一部分。在数据科学的领域中,Python 已成为当之无愧的“首选语言”,其强大的生态系统和简洁的语法让人如虎添…...

【实战】渗透测试下的文件操作
目录 Linux查找文件 Windows查找文件 查找可写目录 windows Linux 创建 Windows Linux 压缩 解压 远程解压文件 Linux查找文件 >find / -name index.php 查找木马文件 >find . -name *.php | xargs grep -n eval( >find . -name *.php | xargs grep -n ass…...

基于深度神经网络的图像防篡改检测方法研究
标题:基于深度神经网络的图像防篡改检测方法研究 内容:1.摘要 随着数字化时代的发展,图像篡改现象日益普遍,严重影响了图像信息的真实性和可靠性。本文旨在研究基于深度神经网络的图像防篡改检测方法,以有效识别被篡改的图像。通过收集大量真…...

vue如何实现前端控制动态路由
在 Vue.js 中,动态路由是一种根据不同用户权限或其他因素动态改变路由列表的功能。这种机制允许开发者根据后端提供的权限数据动态渲染前端路由,实现多用户权限系统,不同用户展示不同的导航菜单。 动态路由的配置 动态路由的配置涉及到前端…...

学成在线--day02
复习知识点 classPath: 类加载路径,也就是jvm找字节码文件的路径,我们自己写的类,以及依赖的包,都会放到这个路径下面用于加载。 跨域问题: 是由于浏览器的同源策略(协议,端口,ip…...

《构建有效的AI代理》学习笔记
原文链接:https://www.anthropic.com/engineering/building-effective-agents 《构建有效的AI代理》学习笔记 一、概述 核心结论 • 成功的AI代理系统往往基于简单、可组合的模式,而非复杂框架。 • 需在性能、成本与延迟之间权衡,仅在必要时增加复杂度…...

Go语言基础:数据类型
一、基础数据类型:Go语言的积木块 1.1 数字类型全家福 package mainimport ("fmt" )func main() {// 有符号整数类型var a int 42 // int 类型,自动选择32或64位var b int8 127 // int…...
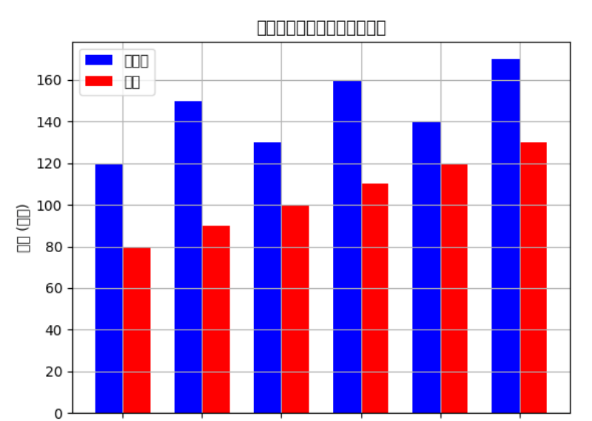
数据处理专题(四)
目标 使用 Matplotlib 进行基本的数据可视化。 学习内容 绘制折线图 绘制散点图 绘制柱状图 代码示例 1. 导入必要的库 import matplotlib.pyplot as pltimport numpy as npimport pandas as pd 2. 创建示例数据集 # 创建示例数据集data { 月份: [1月, 2月, 3…...

【目标检测】【深度学习】【Pytorch版本】YOLOV1模型算法详解
【目标检测】【深度学习】【Pytorch版本】YOLOV1模型算法详解 文章目录 【目标检测】【深度学习】【Pytorch版本】YOLOV1模型算法详解前言YOLOV1的模型结构YOLOV1模型的基本执行流程YOLOV1模型的网络参数YOLOV1模型的训练方式 YOLOV1的核心思想前向传播阶段网格单元(grid cell)…...

云钥科技多通道工业相机解决方案设计
项目应用场景分析与需求挑战 1. 应用场景 目标领域:工业自动化检测(如精密零件尺寸测量、表面缺陷检测)、3D立体视觉(如物体建模、位姿识别)、动态运动追踪(如高速生产线监控)等。 核心…...

从零到一:ESP32与豆包大模型的RTC连续对话实现指南
一、对话效果演示 ESP32与豆包大模型的RTC连续对话 二、ESP-ADF 介绍 乐鑫 ESP-ADF(Espressif Audio Development Framework)是乐鑫科技(Espressif Systems)专为 ESP32 系列芯片开发的一款音频开发框架。它旨在简化基于 ESP32 芯…...

【深度学习与实战】2.3、线性回归模型与梯度下降法先导案例--最小二乘法(向量形式求解)
为了求解损失函数 对 的导数,并利用最小二乘法向量形式求解 的值 这是线性回归的平方误差损失函数,目标是最小化预测值 与真实值 之间的差距。 损失函数: 考虑多个样本的情况,损失函数为所有样本的平方误差之和&a…...

【Django】教程-2-前端-目录结构介绍
【Django】教程-1-安装创建项目目录结构介绍 3. 前端文件配置 3.1 目录介绍 在app下创建static文件夹, 是根据setting中的配置来的 STATIC_URL ‘static/’ templates目录,编写HTML模板(含有模板语法,继承,{% static ‘xx’ …...

JS判断对象是否为空的方法
在 JavaScript 中,判断一个对象是否为空对象(即没有自身可枚举属性),可以通过以下方法实现: 方法 1:使用 Object.keys() javascript function isEmptyObject(obj) {// 确保是普通对象(排除 n…...

详解list容器
1.list的介绍 list的底层结构是双向带头循环链表,允许随机的插入和删除,但其内存空间不是连续的。随机访问空间能力差,需要从头到尾遍历节点,不像vector一样高效支持 2.list的使用 构造函数 1.默认构造函数:创建一个…...
leetcode_977. 有序数组的平方_java
977. 有序数组的平方https://leetcode.cn/problems/squares-of-a-sorted-array/ 1.题目 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1…...

Spring Boot 3.4.3 基于 SpringDoc 2 和 Swagger 3 实现项目接口文档管理
在现代企业级应用开发中,前后端分离已成为主流模式,前端负责界面呈现,后端专注提供 RESTful API 接口。然而,接口文档的编写和维护往往是开发过程中的痛点。Spring Boot 3.4.3 结合 SpringDoc 2 和 Swagger 3,为开发者…...
)
前端面经分享(25/03/26)
北京一家做AI解决方案的公司,技术一面,15k-20k,要求3-5年 你们React项目里路由模式用的什么React里class组件和function组件都用过吗常用Hook,解释一下他们的作用useEffect第二个参数填空数组和不填有什么区别React组件通信的常用…...

Matlab基础知识与常见操作【无痛入门】
【1】Matlab基本概念 【2】Matlab程序设计 【3】Matlab图形绘制 以上三篇文章为Matlab主要的应用场景,我在学习的过程中做一下记录,方便以后回顾。 接下来介绍下Matlab的工作界面,以及如何高效率的应用Matlab的帮助手册。在我看来&#x…...

HTTP协议手写服务器
目录 一、请求的是Web根目录 二、GET方法通过URL传参 三、根据资源类型对应出Content-Type值 四、Http代码 项目完整源代码:Http 周不才/cpp_linux study - 码云 - 开源中国 一、请求的是Web根目录 如果URL中请求的资源是Web根目录,则自动跳转到主…...

网络探索之旅:网络原理(第二弹)
上篇文章,小编分享了应用层和传输层深入的一点的知识,那么接下来,这篇文章,继续分享网络层和数据链路层。 网络层 了解这个网络层,那么其实就是重点来了解下IP这个协议 对于这个协议呢,其实也是和前面的…...

深入剖析 JVM:从组成原理到调优实践
深入剖析 JVM:从组成原理到调优实践 深入剖析 JVM:从组成原理到调优实践一、JVM 组成架构:运行 Java 程序的 “幕后引擎”1.1 内存结构:数据存储的 “分区管理”1.2 执行引擎:字节码的 “翻译官”1.3 本地方法接口&…...

阿里云下一代可观测时序引擎-MetricStore 2.0
作者:徐昊(博澍) 背景 作为可观测场景使用频度最高的数据类型,Metrics 时序数据在可观测领域一直占有着重要地位,无论是从全局视角来观测系统整体状态,还是从大范围数据中定位某一个异常的位置࿰…...

从入门到精通【 MySQL】 数据库约束与设计
文章目录 📕1. 数据库约束✏️1.1 NOT NULL 非空约束✏️1.2 DEFAULT 默认值约束✏️1.3 UNIQUE 唯一约束✏️1.4 PRIMARY KEY 主键约束✏️1.5 FOREIGN KEY 外键约束✏️1.6 CHECK 约束 📕2. 数据库设计✏️2.1 第一范式✏️2.2 第二范式✏️2.3 第三范…...

使用LLaMAFactory微调Qwen大模型
一、环境配置与工具安装 1. 硬件要求 GPU:至少1块NVIDIA GPU(推荐RTX 4090/A100/H100,显存≥16GB)。内存:≥64GB系统内存。存储:≥100GB硬盘空间用于模型与数据集存储。2. 软件依赖 Python 3.8+:需安装CUDA支持的PyTorch版本(如torch==2.0.1+cu117)。 依赖库:通过以…...

Dubbo 通信流程 - 服务的调用
Dubbo 客户端的使用 在 Dubbo 应用中,往类成员注解 DubboReference,服务启动后便可以调用到远端: Component public class InvokeDemoFacade {AutowiredDubboReferenceprivate DemoFacade demoFacade;public String hello(String name){// …...

【数据结构】哈夫曼树
哈夫曼树 在学习哈夫曼树之前,先了解以下几个概念: 一:**路径长度:**在一棵树中,从一个节点到另一个节点所经过的“边”的数量,被我们称为两个节点之间的路径长度。 二:**树的路径长度…...
