Java实现N皇后问题的双路径探索:递归回溯与迭代回溯算法详解
N皇后问题要求在N×N的棋盘上放置N个皇后,使得她们无法互相攻击。本文提供递归和循环迭代两种解法,并通过图示解释核心逻辑。
一、算法核心思想
使用回溯法逐行放置皇后,通过冲突检测保证每行、每列、对角线上只有一个皇后。发现无效路径时回退到上一状态。
冲突检测条件(关键):
- 同列冲突:
col[i] == col[j] - 对角线冲突:
abs(col[i] - col[j]) == abs(i - j)
二、递归版本实现
- 流程图

- 时序图

- 代码解释
:
- 程序目的
该代码用于解决N皇后问题,即在N×N棋盘上放置N个皇后,使其互不攻击(即任意两个皇后不在同一行、列或对角线上),返回所有可能的解。- solveNQueens方法
- 初始化结果列表
result,用于存储所有解。- 调用
backtrack方法启动递归回溯过程。- 参数
n表示棋盘大小,cols数组记录每行皇后所在的列位置(索引为行,值为列)。- backtrack递归核心
- 终止条件:当
row == n时,表示所有皇后已正确放置,将当前cols数组的拷贝加入结果(避免后续修改影响结果)。- 递归逻辑:遍历当前行的每一列
col,若位置有效则放置皇后(cols[row] = col),并递归处理下一行(row + 1)。- isValid冲突检查
- 检查当前列
col与之前所有行(0到row-1)的皇后是否冲突:
- 列冲突:
cols[i] == col,即同一列已有皇后。- 对角线冲突:
Math.abs(col - cols[i]) == row - i,即行差等于列差绝对值。- 若任一条件满足,返回
false,否则位置有效。- 主函数测试与输出
- 测试
n=4的皇后问题,调用solveNQueens获取所有解。- 使用Lambda表达式遍历打印每个解(如
[1, 3, 0, 2]表示第0行皇后在1列,第1行在3列等)。- 关键实现细节
- 回溯剪枝:仅尝试有效位置,减少递归次数。
- 结果存储:每次成功时创建新的
ArrayList保存当前解,避免引用问题。- 递归层次:每层递归处理一行皇后,确保每行只有一个皇后。
示例输出:
对于n=4,输出两个解:[1, 3, 0, 2]和[2, 0, 3, 1],对应两种不同的棋盘布局方式。
- 代码实现
- 注意:下标从0开始
import java.util.ArrayList;
import java.util.List;public class NQueensRecursive {public static List<List<Integer>> solveNQueens(int n) {List<List<Integer>> result = new ArrayList<>();backtrack(n, 0, new Integer[n], result);return result;}private static void backtrack(int n, int row, Integer[] cols, List<List<Integer>> result) {if (row == n) {result.add(new ArrayList<>(List.of(cols)));return;}for (int col = 0; col < n; col++) {if (isValid(cols, row, col)) {cols[row] = col;backtrack(n, row + 1, cols, result);}}}private static boolean isValid(Integer[] cols, int row, int col) {for (int i = 0; i < row; i++) {if (cols[i] == col || Math.abs(col - cols[i]) == row - i) {return false;}}return true;}public static void main(String[] args) {List<List<Integer>> solutions = solveNQueens(4);solutions.forEach(System.out::println);}
}

三、循环迭代版本实现
- 时序图

- 流程说明
- 初始化阶段:
- 清空皇后位置数组
- 从第一个皇后开始放置(j=1)
- 主循环逻辑:
- 每次循环尝试将当前皇后的位置右移一格
- 通过check()验证当前位置是否:
- 与已有皇后同列
- 处于同一斜线
- 合法时继续处理下一个皇后,非法时继续右移
- 当完成最后一列放置时输出有效方案
- 回溯机制:
- 当某列所有位置尝试失败后
- 重置当前列位置为0
- 回溯到前一列继续尝试新位置
- 终止条件:
- 当回溯到j=0时说明所有可能性已穷尽
- 程序正常结束
该实现通过非递归方式实现了经典的回溯算法,使用while循环和位置重置机制替代了递归调用栈,具有较好的空间效率。
- 代码实现
- 注意:下标从1开始
public class Test {// 定义4个皇后static final Integer N = 4;// 存储皇后的列号static int[] q = new int[N+1];// 方案数static int answer =0;public static void main(String[] args) {queen();}public static boolean check(int j){for(int i=1;i<j;i++){if(q[i]==q[j] || Math.abs(i-j)==Math.abs(q[i]-q[j])){ // 判断是否同列或同一斜线return false;}}return true;}public static void queen(){queenInit();int j = 1; // 表示正在摆放第j个皇后while(j>=1){q[j] ++;// 让第j个皇后的位置加1while(!check(j) && q[j]<=N){ // 不满足条件的话,就一直向后移动,为了防止越界,还需要判断q[j]的长度q[j]++;}// 判断if(q[j]<=N){// 表示第j个位置,合法if(j==N){// 最后一个皇后已经摆放完毕了answer++;System.out.print("方案"+answer);System.out.print("结果为:");for (int i = 1; i <=N ; i++) {System.out.print(q[i]+",");}System.out.println();}else{// 继续找下一个皇后的摆放位置j++;}}else{// 没有位置摆放了,需要回溯到上一次。q[j]=0; // 重置位置j--;}}}// 皇后初始化public static void queenInit(){for(int i=1;i<=N;i++){q[i]=0;}}
}
四、算法流程图示(以4皇后为例)
步骤分解:
1. 放置行0的皇后在列0Q . . .. . . .. . . .. . . .2. 行1尝试列0(冲突)→ 尝试列1(冲突)→ 列2有效Q . . .. . Q .. . . .. . . .3. 行2尝试所有列均冲突,回溯到行1Q . . .. . . . ← 行1无法继续. . . .. . . .4. 行1移动到列3Q . . .. . . Q. . . .. . . .5. 行2尝试列1有效Q . . .. . . Q. Q . .. . . .6. 行3无有效列,回溯→最终找到解:[1, 3, 0, 2] 对应棋盘:. Q . .. . . QQ . . .. . Q .
五、算法对比
| 特性 | 递归版本 | 循环迭代版本 |
|---|---|---|
| 代码复杂度 | 简洁,易理解 | 需手动管理状态栈 |
| 内存消耗 | 有栈深度限制 | 显式栈结构,可控性强 |
| 适用场景 | 小规模数据,代码可读性优先 | 避免栈溢出,大数据量更稳定 |
两种方法时间复杂度均为O(N!),实际效率相近,选择依据具体场景需求。
相关文章:

Java实现N皇后问题的双路径探索:递归回溯与迭代回溯算法详解
N皇后问题要求在NN的棋盘上放置N个皇后,使得她们无法互相攻击。本文提供递归和循环迭代两种解法,并通过图示解释核心逻辑。 一、算法核心思想 使用回溯法逐行放置皇后,通过冲突检测保证每行、每列、对角线上只有一个皇后。发现无效路径时回退…...

【代码艺廊】pyside6桌面应用范例:homemade-toolset
在研发测试日常工作中,通常会遇到很多琐碎的事情,占用我们工作的时间和精力,从而导致我们不能把大部分的注意力放在主要的工作上面。为了解决这个问题,除了加人之外,我们通常会开发一些日常用的效率工具,比…...

LeetCode 3047 求交集区域内的最大正方形面积
探寻矩形交集中的最大正方形面积 在算法与数据结构的探索之路上,二维平面几何问题一直占据着独特的地位,它们不仅考验我们的空间思维能力,还要求我们能够巧妙地运用算法逻辑。今天,我们将深入剖析一道极具代表性的二维平面几何算…...

谷歌开源单个 GPU 可运行的Gemma 3 模型,27B 超越 671B 参数的 DeepSeek
自从 DeepSeek 把训练成本打下来之后,各个模型厂家现在不再堆参数进行模型的能力对比。而是转向了训练成本优化方面,且还要保证模型能力不减反增的效果。包括使用较少的模型参数,降低 GPU 使用数量,降低模型内存占用等等技术手段。…...

C++_类和对象(下)
【本节目标】 再谈构造函数Static成员友元内部类匿名对象拷贝对象时的一些编译器优化再次理解封装 1. 再谈构造函数 1.1 构造函数体赋值 在创建对象时,编译器通过调用构造函数,给对象中各个成员变量一个合适的初始值。 class Date { public:Date(in…...

《Java实战:素数检测算法优化全解析——从暴力枚举到筛法进阶》
文章目录 摘要一、需求分析二、基础实现代码与问题原始代码(暴力枚举法)问题分析 三、优化版代码与解析优化1:平方根范围剪枝优化2:偶数快速跳过完整优化代码 四、性能对比五、高阶优化:埃拉托斯特尼筛法算法思想代码实…...

基于Python+Flask的服装零售商城APP方案,用到了DeepSeek AI、个性化推荐和AR虚拟试衣功能
首先创建项目结构: fashion_store/ ├── backend/ │ ├── app/ │ │ ├── __init__.py │ │ ├── models/ │ │ ├── routes/ │ │ ├── services/ │ │ └── utils/ │ ├── config.py │ ├── requirements.t…...

二,<FastApi>FastApi的两个核心组件
FastAPI的两个核心组件Pydantic和Starlette。 Starlette 负责Web部分(Asyncio),Starlette Starlette是一个轻量级的ASGI框架/工具包,非常适合在Python构建异步Web服务。 它已经准备好生产,并为您提供以下内容: 轻巧的低复杂性HTTP Web框架。W…...

Docker设置代理
目录 前言创建代理文件重载守护进程并重启Docker检查代理验证 前言 拉取flowable/flowable-ui失败,用DaoCloud源也没拉下来,不知道是不是没同步。索性想用代理拉镜像。在此记录一下。 创建代理文件 创建docker代理配置 sudo mkdir -p /etc/systemd/s…...

一键自动备份:数据安全的双重保障
随着数字化时代的到来,数据已成为企业和个人不可或缺的核心资产。在享受数据带来的便捷与高效的同时,数据丢失的风险也随之增加。因此,备份文件的重要性不言而喻。本文将深入探讨备份文件的重要性,并介绍两种实用的自动备份方法&a…...

HeidiSQL:多数据库管理工具
HeidiSQL 是一款广受欢迎的免费开源数据库管理工具,专为数据库管理员及开发者设计。无论您是刚接触数据库领域的新手,还是需要同时处理多种数据库系统的专业开发者,该工具都能凭借其直观的界面和强大的功能,助您轻松完成数据管理任…...

医药档案区块链系统
1. 医生用户模块 目标用户:医护人员 核心功能: 检索档案:通过关键词或筛选条件快速定位患者健康档案。请求授权:向个人用户发起档案访问权限申请,需经对方确认。查看档案…...

【Python学习】列表/元组等容器的常用内置函数详解
文章目录 map使用示例: filter示例:注意事项: sortedsorted() 与 list.sort() 的区别: any示例: all示例: any 与 all 的对比zip示例:常见用途: enumerate示例:常见用途&…...

蓝桥云客--浓缩咖啡液
4.浓缩咖啡液【算法赛】 - 蓝桥云课 问题描述 蓝桥杯备赛选手小蓝最近刷题刷到犯困,决定靠咖啡续命。他手上有 N 种浓缩咖啡液,浓度分别是 A1%, A2%, …, AN%,每种存货都是无限的。为了提神又不炸脑,小蓝需要按比例混合这…...

SQLark(百灵连接):一款面向信创应用开发者的数据库开发和管理工具
SQLark(百灵连接)是一款面向信创应用开发者的数据库开发和管理工具,用于快速查询、创建和管理不同类型的数据库系统。 目前可以支持达梦数据库、Oracle 以及 MySQL。 SQL 智能编辑器 基于语法语义解析实现代码补全能力,为你提供…...

计算机视觉——为什么 mAP 是目标检测的黄金标准
概述 在目标检测领域,有一个指标被广泛认为是衡量模型性能的“黄金标准”,它就是 mAP(Mean Average Precision,平均精确率均值)。如果你曾经接触过目标检测模型(如 YOLO、Faster R-CNN 或 SSD)…...

Frame Of Reference压缩算法
文章目录 1_概述2_算法基本步骤3_过程优化4_优势以及局限5_模拟实现6_总结 1_概述 Frame of Reference(FoR)压缩算法 是一种用于压缩数值数据的算法,特别是在处理大规模数据集时,利用数据的局部性和重复性来减少存储和传输的开销…...

1.0 软件测试全流程解析:从计划到总结的完整指南
软件测试全流程解析:从计划到总结的完整指南 摘要 本文档详细介绍了软件测试的完整流程,包括测试计划、测试设计、测试执行、测试报告和测试总结等主要阶段。每个阶段都从目标、主要工作、输出物和注意事项等方面进行了详细说明。通过本文档࿰…...

嵌入式AI简介
嵌入式AI是一种将人工智能算法部署在终端设备中运行的技术,使智能硬件能够在本地实时完成感知、交互和决策功能,无需依赖云端计算。以下是其核心要点: 一、核心特点 1. 本地化处理:数据在设备端直接处理,无需联网&a…...

esp32cam 开发板搭载ov3660摄像头在arduino中调用kimi进行图像识别
首先呢,最近搞一个项目,需要一个摄像头拍摄图片 就买了个ov3660开发板,用的esp32S芯片 淘宝商家给的教程是arduino的,所以先用arduino跑起来 arduino配置esp32-cam开发环境 - 简书1、安装arduino https://www.arduino.cc/en/Main/Software?setlang=cn 2、配置esp32 打开…...

二十种中药果实识别分类系统,Python/resnet18/pytorch
二十种中药果实识别分类系统,Python/resnet18/pytorch 基于pytorch训练, resnet18网络,可用于训练其他分类问题,也可自己重新训练 20类中药材具体包括:(1) 补骨脂,(2) 草豆蔻,(3) 川楝子,(4) 地肤子&…...

如何实现两个视频融合EasyCVR平台的数据同步?详细步骤指南
有用户咨询,现场需要数据库同步,如何将两个EasyCVR平台的数据进行同步呢? 这篇文章我们将详细介绍如何通过简单的接口调用,高效完成两个平台的数据同步操作。 1)获取token 使用Postman调用登录接口,获取…...

WindowsPE文件格式入门05.PE加载器LoadPE
https://bpsend.net/thread-316-1-1.html LoadPE - pe 加载器 壳的前身 如果想访问一个程序运行起来的内存,一种方法就是跨进程读写内存,但是跨进程读写内存需要来回调用api,不如直接访问地址来得方便,那么如果我们需要直接访问地址,该怎么做呢?.需要把dll注进程,注进去的代码…...
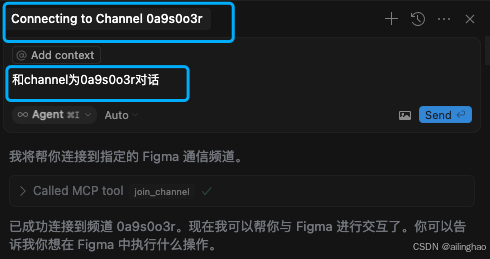
使用Cusor 生成 Figma UI 设计稿
一、开发环境 系统:MacOS 软件版本: Figma(网页或APP版) 注:最好是app版,网页版figma 没有选项 import from manifest app下载地址:Figma Downloads | Web Design App for Desktops & …...

Golang的文件同步与备份
Golang的文件同步与备份 一、Golang介绍 也称为Go语言,是谷歌开发的一种编程语言,具有高效的并发编程能力和出色的内存管理。由于其快速的编译速度和强大的标准库,Golang在网络应用、云平台和大数据等领域得到了广泛应用。 二、文件同步与备份…...

如何用人工智能大模型,进行作业批改?
今天我们学习人工智能大模型如何进行作业批改。手把手学习视频请访问https://edu.csdn.net/learn/40402/666452 第一步,进入讯飞星火。打开google浏览器,输入百度地址后,搜索”讯飞星火”,在搜索的结果中,点第一个讯飞…...

MATLAB之数据分析图系列 三
三维堆叠柱状图 Bar3StackPlot.m文件 clc; clear; close all; %三维堆叠柱状图 %% 数据准备 % 读取数据 load data.mat % 初始化 dataset X; s 0.4; % 柱子宽度 n size(dataset,3); % 堆叠组数%% 图片尺寸设置(单位:厘米) figureUnits c…...

python爬虫:DrissionPage实战教程
如果本文章看不懂可以看看上一篇文章,加强自己的基础:爬虫自动化工具:DrissionPage-CSDN博客 案例解析: 前提:我们以ChromiumPage为主,写代码工具使用Pycharm(python环境3.9-3.10) …...

一、STM32简介
一、实验器材介绍 二、STM32简介 1.STM32 名词解释 STM32是ST公司基于ARM Cortex-M内核开发的32位微控制器。 ST,指ST公司(意法半导体);M,MicroController 微控制器(MCU,MicroController Unit 微控制器单元/单片机&…...

[ctfshow web入门] web2
前置知识 js是可以写在网页中,用于控制网页行为,例如现在表现出无法使用F12,常见用法校验前台登录时输入的邮箱格式是否正确 view-source协议是一种早期就存在的协议,基本上所有主流浏览器都支持这一协议,因此用户…...
