关于深度学习中内部协变量偏移问题小记
内部协变量偏移问题
内部协变量偏移(Internal Covariate Shift,简称ICS)是深度学习中一个重要的概念,用来描述神经网络在训练过程中,各层输入分布发生变化的现象。这种分布偏移会导致训练不稳定、收敛变慢甚至失败。2015年,Ioffe和Szegedy在提出批量归一化(Batch Normalization)的论文中首次系统化地定义了这一问题,并提供了解决方案。
下面我将从定义、原因、影响、解决方法及其意义等方面深入讲解内部协变量偏移。
1. 内部协变量偏移的定义
内部协变量偏移指的是在深度神经网络训练过程中,由于参数更新(如权重和偏置的变化),导致每一层输入的分布发生变化的现象。不同于传统机器学习中的协变量偏移(输入数据分布随时间变化),ICS发生在网络内部,是层与层之间的动态变化。例如,在一个 3 3 3层网络中,第一层输出是第二层的输入,若第一层权重更新后,第二层输入的均值从 0.5 0.5 0.5变为 1.2 1.2 1.2,方差从 1 1 1变为 2 2 2,这就是ICS。
从数学角度看,假设第 l l l层的输入为 x ( l ) x^{(l)} x(l),其分布为 P ( x ( l ) ) P(x^{(l)}) P(x(l)),随着训练迭代, P ( x ( l ) ) P(x^{(l)}) P(x(l))会不断变化,而网络的目标是让每一层的输出适应其参数的当前状态。这种分布的不稳定性就是内部协变量偏移的核心。
2. 内部协变量偏移的原因
ICS的产生主要源于深度网络的层级结构和参数更新机制:
- 参数更新:在反向传播中,每一层的权重 W ( l ) W^{(l)} W(l)和偏置 b ( l ) b^{(l)} b(l)都会根据梯度下降更新。例如,若第一层权重从 W ( 1 ) = [ 0.1 , 0.2 ] W^{(1)} = [0.1, 0.2] W(1)=[0.1,0.2]变为 [ 0.3 , 0.4 ] [0.3, 0.4] [0.3,0.4],其输出 x ( 2 ) = W ( 1 ) x ( 1 ) + b ( 1 ) x^{(2)} = W^{(1)}x^{(1)} + b^{(1)} x(2)=W(1)x(1)+b(1)的分布会随之改变。
- 非线性激活:激活函数(如ReLU、sigmoid)会放大或压缩输入分布的变化。例如,若输入从 [ − 1 , 1 ] [-1, 1] [−1,1]变为 [ − 2 , 2 ] [-2, 2] [−2,2],经过sigmoid后输出范围仍被限制在 [ 0 , 1 ] [0, 1] [0,1],但分布形状会显著不同。
- 深层累积效应:网络越深,前层变化对后层的影响越大。例如,一个 10 10 10层网络中,第一层均值偏移 0.1 0.1 0.1可能导致第 10 10 10层均值偏移 1.5 1.5 1.5,方差放大数倍。
3. 内部协变量偏移的影响
ICS对神经网络训练有显著的负面影响:
- 学习率敏感:由于分布不断变化,学习率需要小心调整。例如,若学习率过高(如 0.1 0.1 0.1),参数更新可能导致输入分布剧烈震荡,梯度爆炸;若过低(如 0.001 0.001 0.001),则收敛过慢。
- 梯度问题:分布偏移可能使某些层的输入落入激活函数的饱和区。例如,sigmoid函数在输入很大(如 10 10 10)或很小(如 − 10 -10 −10)时,梯度接近 0 0 0,导致梯度消失。
- 训练不稳定:每一层需要不断适应前层输出的新分布。例如,若第 5 5 5层输入均值从 0 0 0变为 5 5 5,该层可能需要重新学习合适的权重,延长训练时间。
一个直观的例子是,在训练一个 20 20 20层网络时,若不处理ICS,前几轮迭代中第 10 10 10层输入可能从均值 0 0 0、方差 1 1 1变为均值 3 3 3、方差 10 10 10,迫使网络反复调整,难以收敛。
4. 解决内部协变量偏移的方法
为了缓解ICS,最著名且广泛使用的方法是批量归一化(Batch Normalization, BN),此外还有其他策略:
(1) 批量归一化(Batch Normalization)
BN通过标准化每一层的输入,减少分布偏移。具体步骤是:
- 对每一小批量(mini-batch)的输入 x ( l ) x^{(l)} x(l)计算均值 μ B \mu_B μB和方差 σ B 2 \sigma_B^2 σB2,例如一个批量数据 [ 1 , 2 , 3 ] [1, 2, 3] [1,2,3]的 μ B = 2 \mu_B = 2 μB=2, σ B 2 = 1 \sigma_B^2 = 1 σB2=1。
- 标准化: x ^ ( l ) = x ( l ) − μ B σ B 2 + ϵ \hat{x}^{(l)} = \frac{x^{(l)} - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} x^(l)=σB2+ϵx(l)−μB,其中 ϵ \epsilon ϵ是小常数(如 1 0 − 5 10^{-5} 10−5)避免除零。
- 缩放和平移: y ( l ) = γ x ^ ( l ) + β y^{(l)} = \gamma \hat{x}^{(l)} + \beta y(l)=γx^(l)+β, γ \gamma γ和 β \beta β是可学习参数,保持模型表达能力。
例如,若第 3 3 3层输入为 [ 0 , 2 , 4 ] [0, 2, 4] [0,2,4],BN会将其标准化为均值 0 0 0、方差 1 1 1的分布,再通过 γ \gamma γ和 β \beta β调整输出范围。
(2) 其他归一化方法
- 层归一化(Layer Normalization):对每一层的单个样本进行标准化,适用于RNN等场景。
- 权重归一化(Weight Normalization):通过标准化权重矩阵减少输出分布的变化。
(3) 更好的初始化
合理的权重初始化(如Xavier或He初始化)可以减小初始阶段的分布偏移。例如,He初始化使每一层输出的方差保持稳定,缓解ICS。
5. 内部协变量偏移的意义
理解和解决ICS对深度学习至关重要:
- 加速训练:通过BN减少ICS,一个 50 50 50层网络的训练时间可能从数天缩短到数小时。例如,ResNet在加入BN后收敛速度显著提升。
- 允许更大网络:ICS缓解后,超深网络(如 100 100 100层以上)变得可训练。例如,ResNet-152依赖BN成功训练。
- 提高稳定性:模型对学习率和初始值的敏感性降低。例如,使用BN后,学习率从 0.01 0.01 0.01提高到 0.1 0.1 0.1仍能稳定训练。
一个实际案例是,在ImageNet数据集上训练深度网络时,未使用BN的模型可能需要 100 100 100轮才能达到 70 % 70\% 70%精度,而加入BN后可能 50 50 50轮即可实现。
6. 局限性与争议
尽管ICS被广泛讨论,但其重要性也存在争议:
- 实际作用存疑:一些研究表明,BN的成功可能更多来自平滑梯度而非直接减少ICS。例如,移除BN后调整学习率仍能训练深层网络。
- 计算开销:BN增加了均值和方差的计算,例如一个批量 128 128 128样本的网络,每层需额外计算 256 256 256个统计量。
- 小批量问题:当批量大小很小时(如 2 2 2),BN的统计估计不准确,可能加剧分布偏移。
总结
内部协变量偏移是深度神经网络训练中由于参数更新导致的层间输入分布变化问题。它由权重调整、非线性激活和深层累积效应引起,会导致学习率敏感、梯度消失和训练不稳定。例如,一个 10 10 10层网络可能因第一层权重变化,使第 10 10 10层输入分布从均值 0 0 0变为 5 5 5。批量归一化通过标准化输入有效缓解ICS,加速训练并支持超深网络设计。尽管其作用仍有争议,理解ICS仍是优化深度学习模型的关键。
相关文章:

关于深度学习中内部协变量偏移问题小记
内部协变量偏移问题 内部协变量偏移(Internal Covariate Shift,简称ICS)是深度学习中一个重要的概念,用来描述神经网络在训练过程中,各层输入分布发生变化的现象。这种分布偏移会导致训练不稳定、收敛变慢甚至失败。2…...
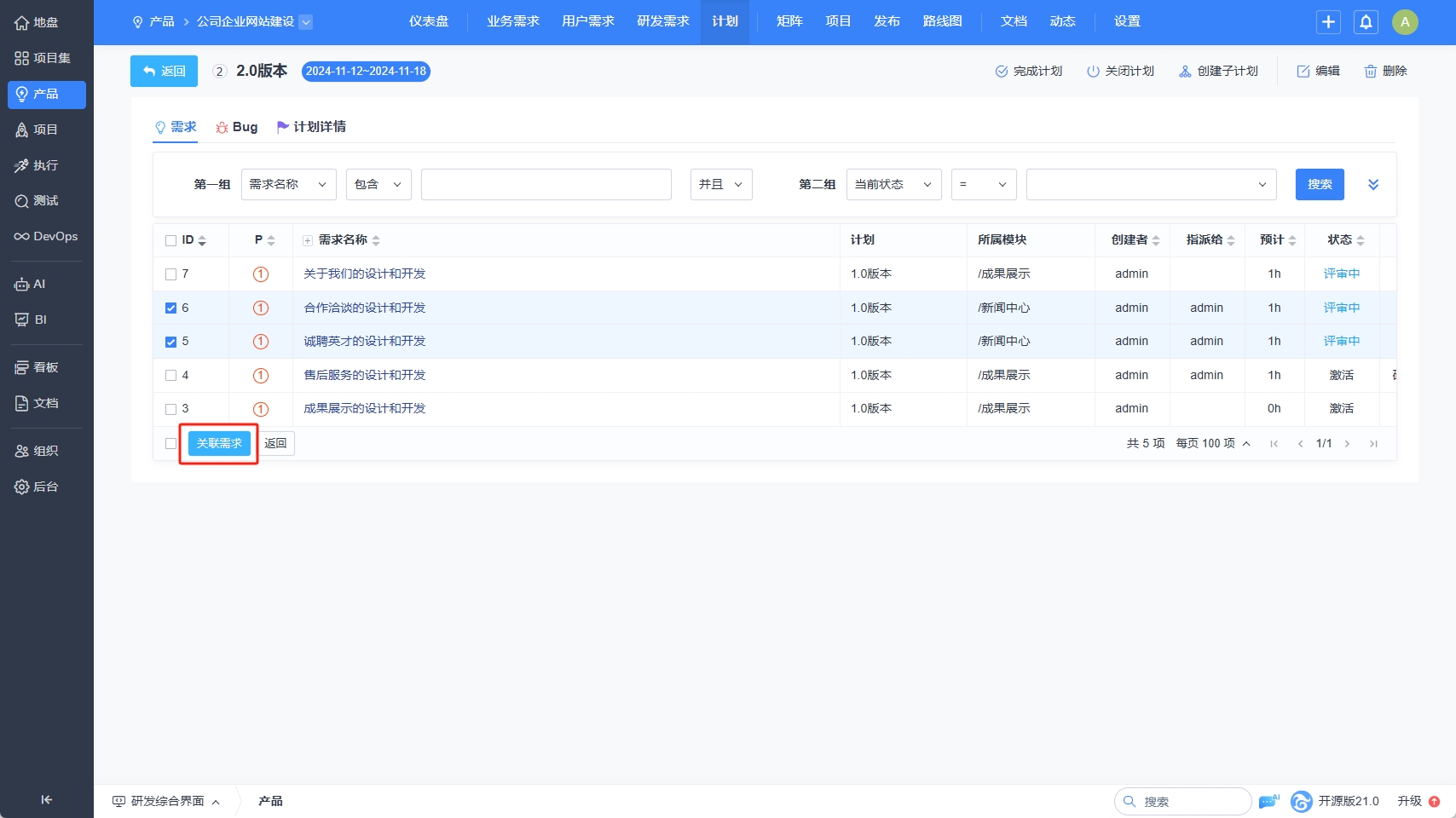
15-产品经理-维护需求
一、提研发需求 在产品–研发需求列表页,点击“提研发需求”按钮, 在提研发需求页面,可以选择已有的计划。也可以在计划页面里进行关联。 未编辑完的需求可以点击【存为草稿】按钮,保存为草稿状态,待编辑完成再选择提…...

JVM基础架构:内存模型×Class文件结构×核心原理剖析
🚀前言 “为什么你的Java程序总在半夜OOM崩溃?为什么某些代码性能突然下降?一切问题的答案都在JVM里! 作为Java开发者,如果你: 对OutOfMemoryError束手无策看不懂GC日志里的神秘数字好奇.class文件如何变…...

js前端对时间进行格式处理
时间格式处理 通过js前端,使用dayjs库进行格式化 安装dayjs库 npm install dayjs 封装成日期格式化工具类 formatter.ts // 导入 dayjs,先安装依赖 npm install dayjs import dayjs from "dayjs"; import utc from "dayjs/plugin/utc…...

如何拿到iframe中嵌入的游戏数据
在 iframe 中嵌入的游戏数据是否能被获取,取决于以下几个关键因素: 1. 同源策略 浏览器的同源策略是核心限制。如果父页面和 iframe 中的内容同源(即协议、域名和端口号完全相同),那么可以直接通过 JavaScript 访问 …...

Chrome 135 版本新特性
Chrome 135 版本新特性 一、Chrome 135 版本浏览器更新 ** 1. 第三方托管账户注册迁移到 OIDC 授权码流程** Chrome 135 将账户注册的登录页面从营销网站迁移到动态网站,同时也将 OpenID Connect (OIDC) 的隐式流程迁移到授权码流程。这样做的目的是进一步提升第…...

基于milvus安装--可视化工具 attu
说明:Attu是Milvus的可视化工具,用于方便地管理和查询向量数据。 1.安装docker 并配置国内镜像 配置国内镜像加速: 1.修改 /etc/docker/daemon.json,设置 registry mirror: sudo vim /etc/docker/daemon.json {"registry-mirrors": ["https://docker.1m…...

【Vue-组件】学习笔记
目录 <<回到导览组件1.项目1.1.Vue Cli1.2.项目目录1.3.运行流程1.4.组件的组成1.5.注意事项 2.组件2.1.组件注册2.2.scoped样式冲突2.3.data是一个函数2.4.props详解2.5.data和prop的区别 3.组件通信3.1.父子通信3.1.1.父传子(props)3.1.2.子传父…...

[蓝桥杯青少年组省赛 2024] 通关游戏的最少能量值
在 Python 中,可以通过以下步骤实现二维数组的输入,并根据数组的第一个元素进行排序: 读取输入:使用 input() 函数读取输入,并将其转换为整数。创建二维数组:将输入的任务的启动能量值和消耗能量值存储为二…...
——理论、应用与实践)
预测函数控制(PFC)——理论、应用与实践
目录 预测函数控制(PFC)——理论、应用与实践一、引言二、预测函数控制的基本原理1. PFC 的核心思想2. 数学建模与公式推导3. 优势与局限优势局限三、典型案例分析案例一:一维动态系统控制案例描述分析案例二:温度调节系统案例描述分析案例三:机器人轨迹跟踪控制案例描述分…...

(PROFINET 转 EtherCAT)EtherCAT/Ethernet/IP/Profinet/ModbusTCP协议互转工业串口网关
型号 协议转换通信网关 PROFINET 转 EtherCAT MS-GW31 概述 MS-GW31 是 PROFINET 和 EtherCAT 协议转换网关,为用户提供两种不同通讯协议的 PLC 进行数据交互的解决方案,可以轻松容易将 EtherCAT 网络接入 PROFINET 网络中,方便扩展&…...

关于sqlsugar实体多层List映射的问题
如上图所示,当一个主表(crm_fina_pay_req)的子表list<文件附件关系表>( List<crm_fina_payreq_evidofpay_relation> )中,还包含有sysfile(SysFile SysFiles)类型的文件信…...

STM32 HAL库 CANFD配置工具
用法说明: 该工具适用于STM32HAL库,可一键生成CANFD的HAL库配置代码。计算依据为HAL库,并参考ZLG标准。 软件界面: 仓库地址: HAL CANFD Init Gen: 适用于STM32控制器的HAL库 版本说明: V1.2.0 &#x…...
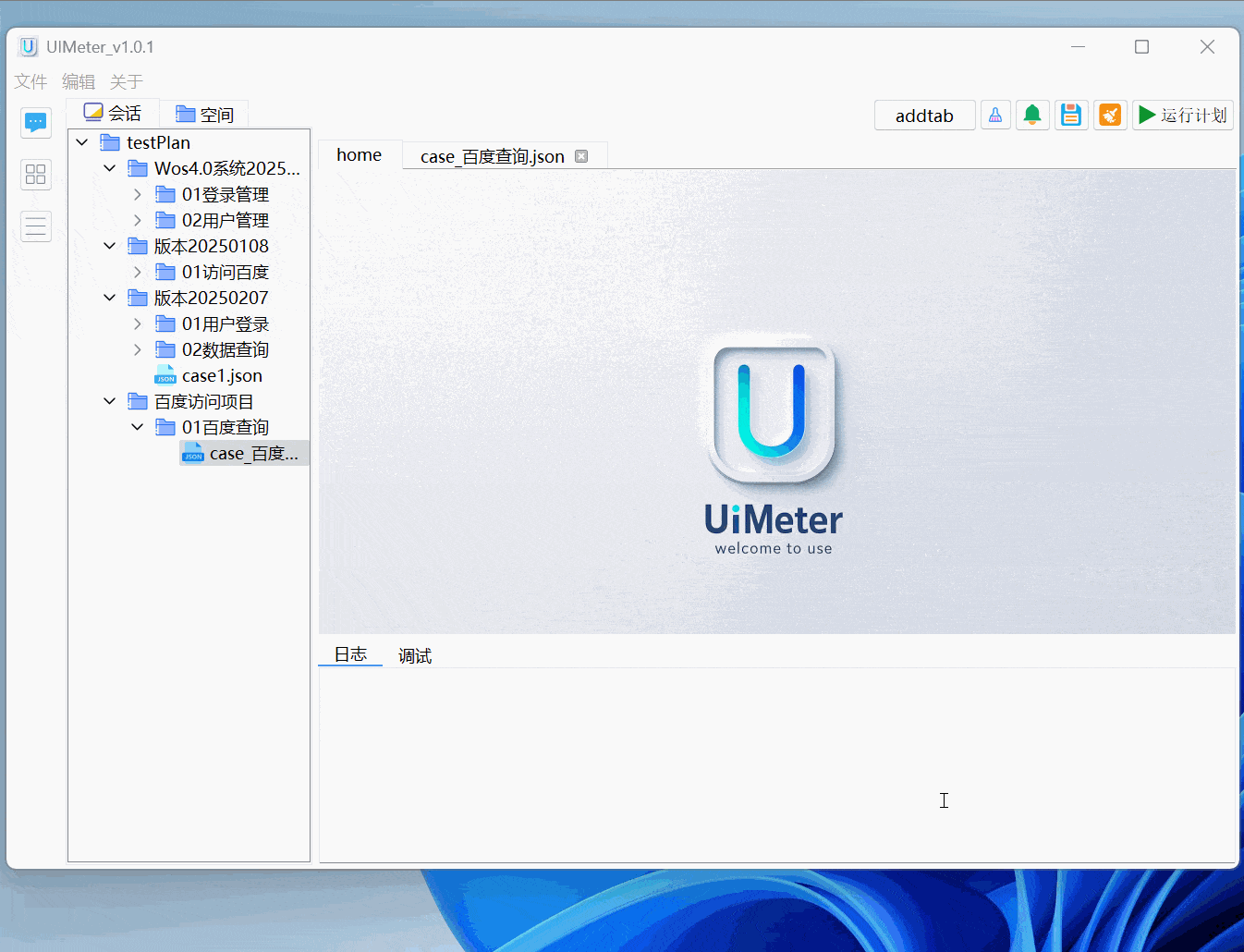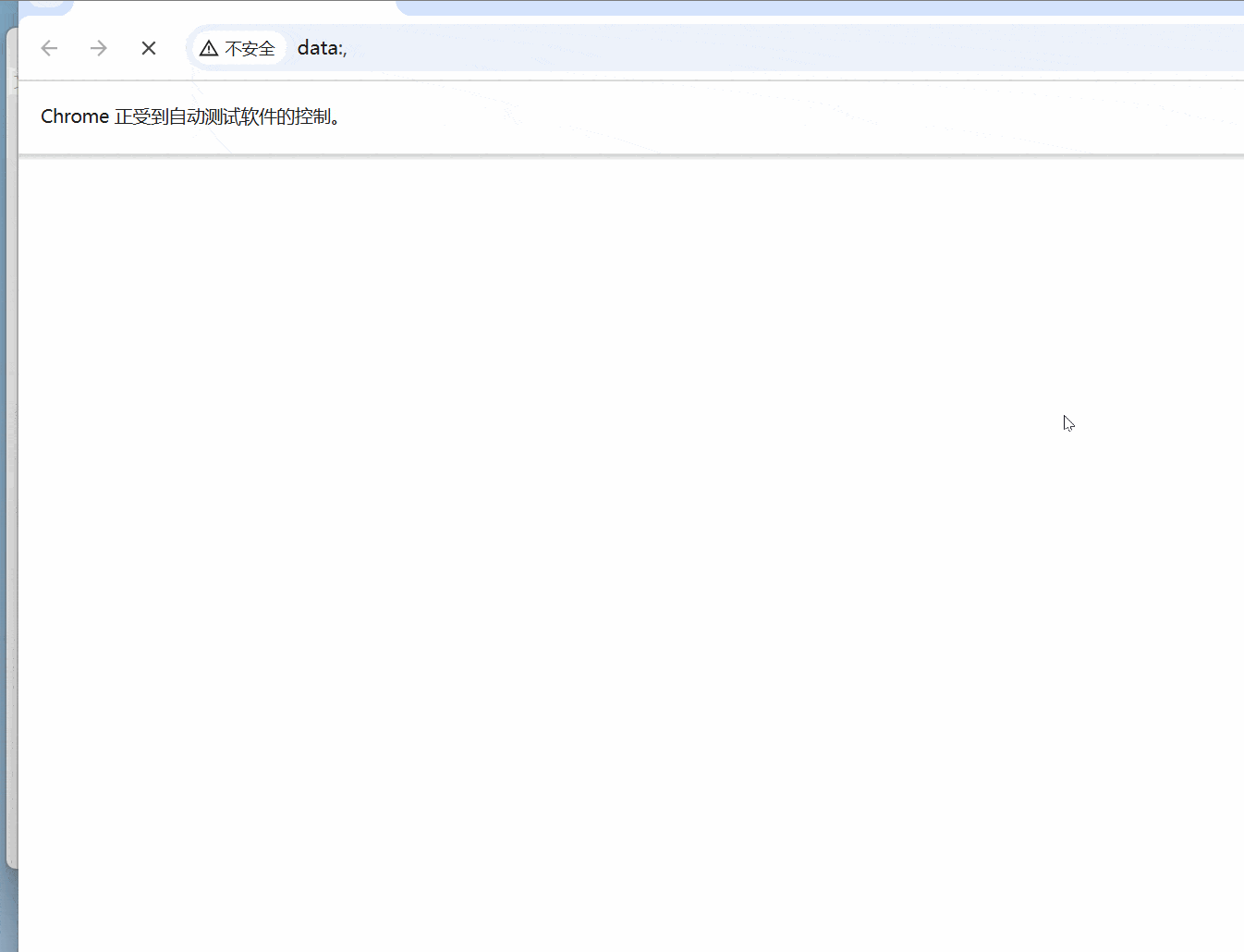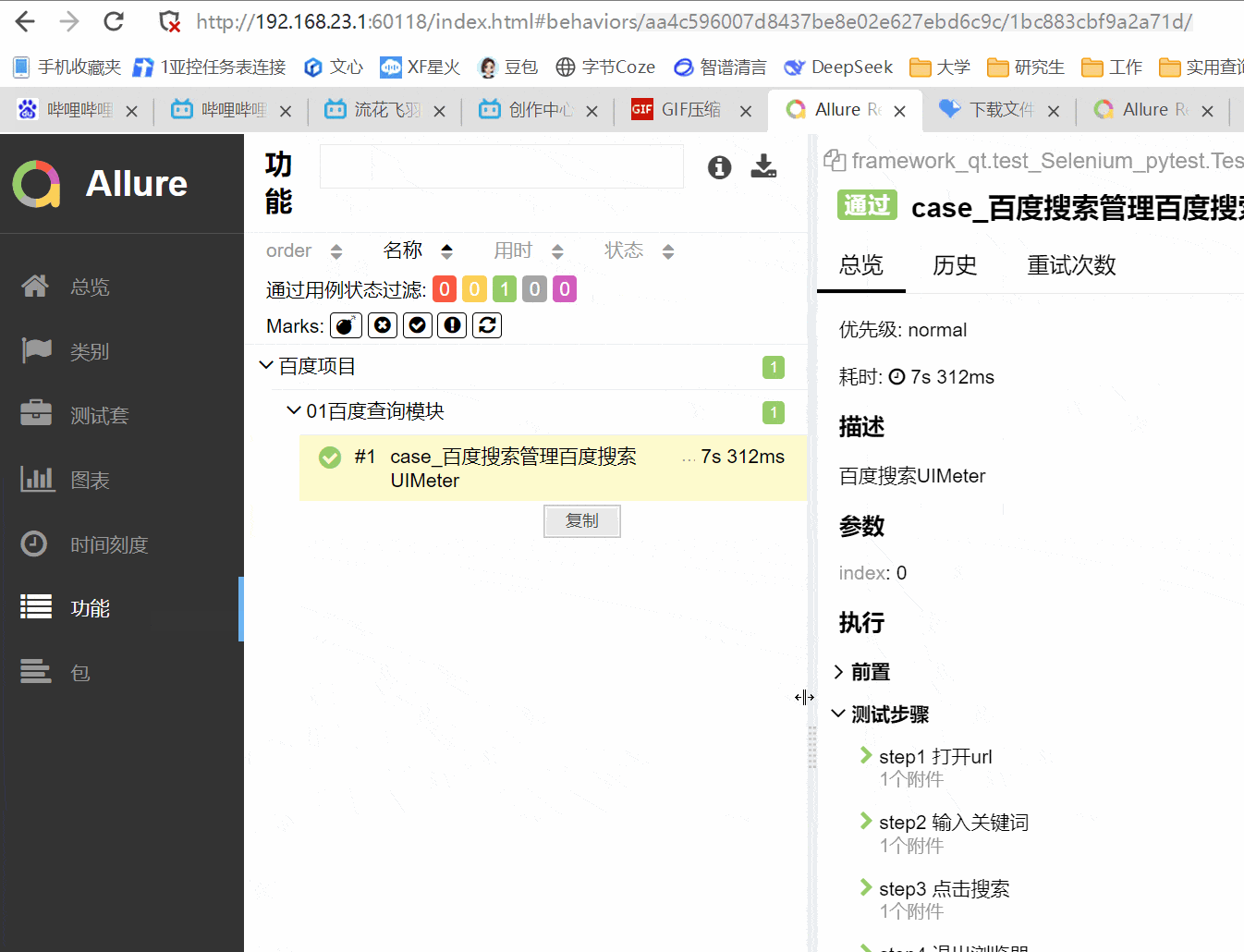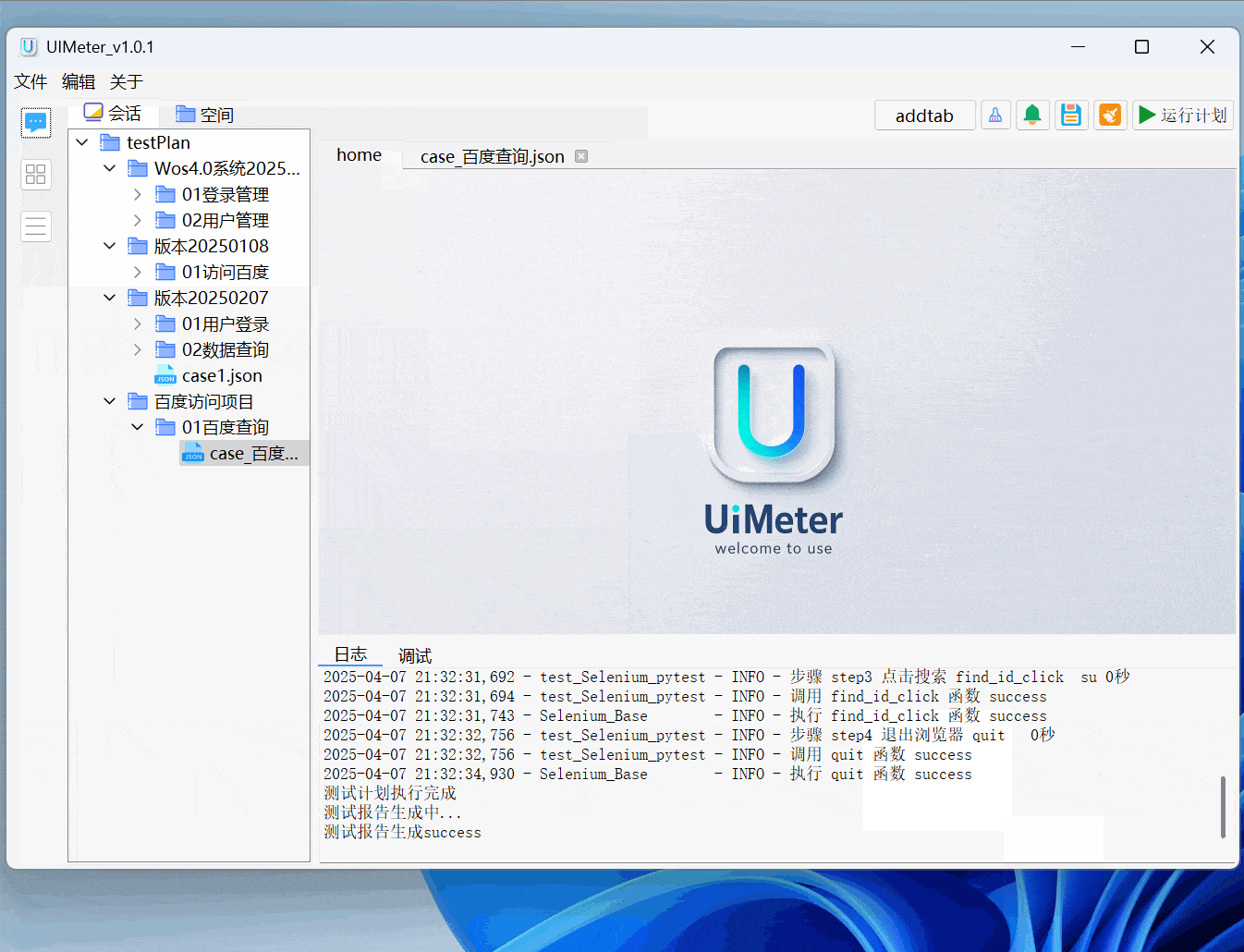
UIMeter-UI自动化软件(产品级)
前言:作为一个资深测试工程师,UI测试,webUI自动化测试是我们必备的技能,我们都知道常用的框架比如selenium、playwright、rebootframwork等等,但是无论哪一种框架,都需要测试人员去编写代码,进行…...

Java面试黄金宝典37
1. 转发与重定向的区别 定义 转发:服务器内部的一种请求处理方式,当客户端向服务器发送请求后,服务器将该请求转发到另一个资源(如 JSP、Servlet)进行处理,整个过程在服务器端完成,客户端并不知道请求被转发,且使用的是同一个请求对象和响应对象。重定向:服务器向客户…...

企业级Java开发工具MyEclipse v2025.1——支持AI编码辅助
MyEclipse一次性提供了巨量的Eclipse插件库,无需学习任何新的开发语言和工具,便可在一体化的IDE下进行Java EE、Web和PhoneGap移动应用的开发;强大的智能代码补齐功能,让企业开发化繁为简。 立即获取MyEclipse v2025.1正式版 具…...

【redis】简介及在springboot中的使用
redis简介 基本概念 Redis,英文全称是Remote Dictionary Server(远程字典服务),是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的API。 与MySQL数据库不…...

隐私计算的崛起:数据安全的未来守护者
在信息技术(IT)的滚滚浪潮中,一种新兴技术正以惊人速度崭露头角——隐私计算(Privacy-Preserving Computation)。2025 年,随着数据泄露事件频发、全球隐私法规日益严格,以及企业对数据协作需求的…...

【Vue-vue基础知识】学习笔记
目录 <<回到导览vue基础知识1.1.创建一个vue实例1.2.vue基础指令1.2.1.v-bind1.2.2.v-model1.2.3.常用事件1.2.4.指令修饰符 1.3.计算属性1.3.1.计算属性的完整写法1.3.2.【案例】成绩 1.4.watch1.4.1.watch属性1.4.2.翻译业务实现1.4.3.watch属性的完整写法1.4.4.【案例…...

Oracle 数据库查询表广播
在 Oracle 数据库中,查询表广播(Broadcast Table)是一种优化分布式查询性能的机制,尤其在并行处理(Parallel Execution)或分布式架构(如 Oracle RAC、Sharding)中。其核心原理是通过…...
)
JavaScript学习教程,从入门到精通,JavaScript 快速入门指南(4)
JavaScript 快速入门指南 在HTML中引入JavaScript 语法知识点: 内部JavaScript:使用<script>标签直接嵌入HTML中外部JavaScript:通过<script src"file.js">引入外部文件推荐将脚本放在<body>末尾或使用defer属…...

网络安全应急响应-文件痕迹排查
在Windows系统的网络安全应急响应中,文件痕迹排查是识别攻击行为的关键步骤。以下是针对敏感目录的详细排查指南及扩展建议: 1. 临时目录排查(Temp/Tmp) 路径示例: C:\Windows\TempC:\Users\<用户名>\AppData\L…...

C++ 提高编程 下
C提高编程 set/multiset 容器set 基本概念set 构造和赋值set 大小和交换set 插入和删除set 查找和统计set 和 multiset 的区别pair 对组创建set 容器排序 map/multimap 容器map 基本概念map 构造和赋值map 大小和交换map 插入和删除map 查找和统计map 容器排序 案例——员工分组…...

【Linux网络】网络套接字socket
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343 🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12891150.html 目录 Socket 编程预备 理解源 IP 地址和目的 IP 地址 认识端口号 端口号范围划分…...

tomcat的负载均衡和会话保持
写你的想写的东西,写在tomcat的默认发布目录中 这里写了一个jsp的文件 访问成功 可以用nginx实现反向代理 tomcat负载均衡实现: 这里使用的算法是根据cookie值进行哈希,根据ip地址哈希会有问题.如果是同一台主机再怎么访问都是同一个ip。 t…...

ffmpeg基础知识入门
文章目录 📦 1. **容器(Container)**✅ 定义:✅ 举例:✅ 功能: 📶 2. **媒体流(Stream)**✅ 定义:✅ 举例:✅ 流和容器关系: …...

c++项目 网络聊天服务器 实现;QPS测试
源码 https://github.com/DBWGLX/SZU_system_programming 文章目录 技术设计编码JSON的替换Protobuf 网络线程池更高效率网络字节序的考虑send可能无法一次性发送全部数据!EPOLLHUP , EPOLLERR 的正确处理 IO数据库操作的更高性能 开发日志2025.3a.粘包问题 2025.4b…...

rnn的音频降噪背后技术原理
rnniose: 这个演示展示了 RNNoise 项目,说明了如何将深度学习应用于噪声抑制。其核心理念是将经典的信号处理方法与深度学习结合,打造一个小巧、快速的实时噪声抑制算法。它不需要昂贵的 GPU —— 在树莓派上就能轻松运行。 相比传统的噪声抑制系统&…...

Python项目打包指南:PyInstaller与SeleniumWire的兼容性挑战及解决方案
前言 前段时间做一个内网开发的需求,要求将selenium程序打包成.exe放在内网的win7上运行,在掘金搜了一圈也没有发现相关文章,因此将过程中踩到的坑记录分享一下。 本文涵盖了具体打包操作、不同模块和依赖项的兼容性解决方案,以…...

【题解】AtCoder AT_abc400_c 2^a b^2
题目大意 我们定义满足下面条件的整数 X X X 为“好整数”: 存在一个 正整数 对 ( a , b ) (a,b) (a,b) 使得 X 2 a ⋅ b 2 X2^a\cdot b^2 X2a⋅b2。 给定一个正整数 N N N( 1 ≤ N ≤ 1 0 18 1\le N\le 10^{18} 1≤N≤1018)ÿ…...
