C++蓝桥杯实训篇（三）

片头

嗨！小伙伴们，大家好~ 今天我们来学习前缀和与差分相关知识，准备好了吗？咱们开始咯！

---

一、一维前缀和

以上，是我们用数学知识求解区间和，现在我们使用前缀和来求解：

 我们知道，求[L，R]的区间和 =>

当L>0时，结果为：sum[R] - sum[L-1] 

当L=0时，结果为：sum[R]

我们可以用代码来实现：

#include<iostream>
using namespace std;const int n = 6;
int sum[n];//求前缀和
int get_sum(int L, int R) 
{if (L == 0) return sum[R];else return sum[R] - sum[L - 1];
}int main() {int arr[n] = { 1,3,7,5,2 };//填充sum数组sum[0] = arr[0];//sum数组的第1个元素和arr数组中的第1个元素的值相同for (int i = 1; i < n; i++) {sum[i] = sum[i - 1] + arr[i];}cout << "[2,4] = " << get_sum(2, 4) << endl;cout << "[0,3] = " << get_sum(0, 3) << endl;cout << "[3,4] = " << get_sum(3, 4) << endl;return 0;
}

 

---

 二、一维差分

以上是利用数学知识求解，如果我们使用差分数组的思想，怎么做呢？

由此，我们得出：求[L，R] + value 时，d[L] + value ，d[R+1] - value

简单证明一下：

我们还可以让差分数组d里面的元素全部初始化为0，这样更方便：

 

 代码实现如下：

#include<iostream>
using namespace std;int d[6] = { 0 };		//差分数组
int sum_d[6] = { 0 };	//前缀和差分数组//根据形参修改差分数组里面的元素
void add(int L, int R, int value) {d[L] += value;d[R + 1] -= value;}int main() {int arr[5] = { 1,3,7,5,2 };add(2, 4, 5);add(1, 3, 2);add(0, 2, -3);//求前缀和差分数组里面的值sum_d[0] = d[0];for (int i = 1; i < 5; i++) {sum_d[i] = sum_d[i - 1] + d[i];}//求新的arr数组for (int i = 0; i < 5; i++) {arr[i] += sum_d[i];cout << arr[i] << " ";}//清除差分数组里面的数据memset(d, 0, sizeof(d));cout << endl;return 0;
}

---

第1题  大学里的树木要维护

这道题，运用到了我们刚刚学的前缀和的思想。 

#include <iostream>
using namespace std;const int N = 100086;
int a[N];
int sum[N];//求[L,R]的区间和
int price(int L,int R){if(L == 1) return sum[R];else return sum[R] - sum[L-1];
}int main()
{int n;     //总共有多少棵树cin >> n;int m;     //总共有多少个区间cin >> m;for(int i = 1; i<= n; i++){cin >> a[i];}//前缀和sum[0] = a[0];for(int i = 1; i<=n; i++){sum[i] = sum[i-1] + a[i];}int L = 0,R = 0;while(m--){cin >> L >> R;cout<<price(L,R)<<endl;}return 0;
}

我们还可以将代码优化：

#include <iostream>
using namespace std;const int N = 100086;
int a[N];
int sum[N];int main()
{int n,m;cin >> n >> m;for(int i = 1; i<= n; i++){cin >> a[i];sum[i] = sum[i-1] + a[i];   //可以一边输入a[i],一边计算sum[i]}int left = 0,right = 0;while(m--){cin >> left >> right;cout<<sum[right]-sum[left-1]<<endl; //如果left==1,left-1==0,sum[0] = 0//若left为1,结果仍然是sum[right]}return 0;
}

---

 三、二维前缀和

一维的前缀和求的只是一排序列的和值，宏观上看，是一条线段、一段区间。

但是二维的前缀和求的是一个矩形的和值，我们用图来表示，假设存在一个二维数组 ，从（1，1）到（4，4）。

我们需要求中间的小矩形的和值，那么应该如何快速求解呢？

3.2 二位前缀数组 

我们定义前缀和数组  为从（1，1）~（i，j）的和值，例如下图：

 那么如何快速求解从（2，2）~（3，3）的和值呢？

我们利用一下容斥的思想，可以得到：

我们用图表示：

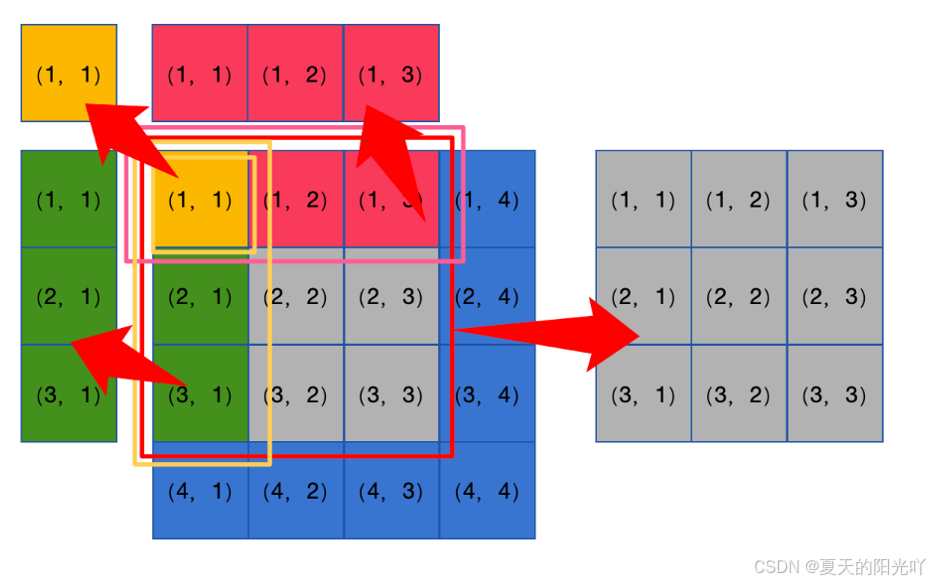
 可以看到，我们尝试从灰色的部分剥离出多余的矩形，但是当减去了红色和绿色的部分后，发现黄色的部分被多减去了1次，因此需要加回来。

那么如何求维护二位前缀和呢？

我们用递推的思想，假设我们要求  ，我们以及知道了  ，那么我们可以用  求出  ，如图：

  打个比方吧：

第2题 二维前缀和

 

 对于这道题，我们采用二位前缀和来求解：

先定义n行m列的二维数组，接着我们可以一边填写值一边将行累加

const int N = 1e3 + 10;  // 定义矩阵最大尺寸为1000+10(缓冲)
typedef long long ll;    // 使用long long类型防止大数溢出ll sum[N][N];  // 二维前缀和数组
ll a[N][N];    // 原始矩阵数据
int n, m, q;   // n行m列的矩阵，q次查询cin >> n >> m >> q;  // 输入矩阵行列数和查询次数for (int i = 1; i <= n; i++) {// 第一步: 计算每行的前缀和for (int j = 1; j <= m; j++) {cin >> a[i][j];sum[i][j] = sum[i][j - 1] + a[i][j];  // 行前缀和}}

计算完行前缀和后，因为是二维前缀和，我们还需要将上方的前缀和累加进来

	cin >> n >> m >> q;  // 输入矩阵行列数和查询次数for (int i = 1; i <= n; i++) {// 第一步: 计算每行的前缀和for (int j = 1; j <= m; j++) {cin >> a[i][j];sum[i][j] = sum[i][j - 1] + a[i][j];  // 行前缀和}// 第二步: 将上方的前缀和累加进来for (int j = 1; j <= m; j++) {sum[i][j] += sum[i - 1][j];  // 列前缀和累加}}

总的来说，前缀和计算分为两步：

① 先计算每行的前缀和（一维前缀和）

② 再将上方行的前缀和累加进来（转化为二维前缀和）

接着我们可以计算从（x1,y1) ~ (x2,y2) 之间的前缀和了

ll get_sum(int x1, int y1, int x2, int y2) {if (x1 > x2 || y1 > y2) return 0;	//越界处理return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}

 这个函数使用前缀和数组快速计算子矩阵和，公式为：

sum = 右下角前缀和 - 上方前缀和 - 左侧前缀和 + 左上角前缀和

OK，我们再回到main函数中调用q次get_sum函数，最后将结果输出即可。

	while(q--) {int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;cout << get_sum(x1, y1, x2, y2) << endl;}

完整代码如下：

#include <iostream>
using namespace std;const int N = 1e3 + 10;  // 定义矩阵最大尺寸为1000+10(缓冲)
typedef long long ll;    // 使用long long类型防止大数溢出ll sum[N][N];  // 二维前缀和数组
ll a[N][N];    // 原始矩阵数据
int n, m, q;   // n行m列的矩阵，q次查询ll get_sum(int x1, int y1, int x2, int y2) {if (x1 > x2 || y1 > y2) return 0;	//越界处理return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}int main() {//n行m列的矩阵//询问q次cin >> n >> m >> q;  // 输入矩阵行列数和查询次数for (int i = 1; i <= n; i++) {// 第一步: 计算每行的前缀和for (int j = 1; j <= m; j++) {cin >> a[i][j];sum[i][j] = sum[i][j - 1] + a[i][j];  // 行前缀和}// 第二步: 将上方的前缀和累加进来for (int j = 1; j <= m; j++) {sum[i][j] += sum[i - 1][j];  // 列前缀和累加}}while(q--) //调用q次{int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;cout << get_sum(x1, y1, x2, y2) << endl;}return 0;
}

---

 第3题  求和

其实这道题是一道数学问题，正好运用到了我们今天学的前缀和方法，一起来看看~

 okk，理解清楚题意后，咱们开始写代码啦~

#include <iostream>
using namespace std;typedef long long ll;          // 定义ll为long long类型，防止大数溢出
const int N = 2e5 + 100;       // 定义数组最大大小，多100作为缓冲
ll a[N];    // 存储输入的原始数组
ll sum[N];  // 存储前缀和数组
int n;      // 存储元素个数int main() {cin >> n;  // 输入元素个数nfor (int i = 1; i <= n; i++) {cin >> a[i];                // 输入第i个元素sum[i] = sum[i - 1] + a[i]; // 计算前缀和：sum[i] = a[1] + a[2] + ... + a[i]}ll ret = 0;	 // 初始化结果为0for (int i = 1; i <= n; i++) {ret += sum[i - 1] * a[i];  // 累加前i-1个元素的和乘以当前元素}cout << ret << endl;  // 输出最终结果return 0;
}

---

 第4题 异或和之和

 代码如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int inf = 1e18;
const int N = 1e5+10;
/*
1.异或的自反性 a^b^b=a  al^...^ar = Sl-1 ^ Sr = (a1^a2^...^al-1) ^ (a1^a2^...^al-1) ^ (^al^...^ar)
2.比如异或运算的计算原理的方面。可以考虑把每个数按二进制拆分，在每一位上统计该位的贡献。2^i贡献
3.只有1有贡献，求区间异或和为1的子段数量 --->Sl^Sr=1  Sl=0 Sr=1 数量相乘O(n*V）
*/
void solve()
{int n;cin >> n;vector<int>a(n + 1);for (int i = 1; i <= n; i++)cin >> a[i];vector<int>s(n + 1);int num1, num0;int ans = 0;for (int i = 0; i <= 20; i++)//第i位{num1 = num0 = 0;num0 += 1;for (int j = 1; j <= n; j++)//第j个数{int num = (a[j] >> i) & 1;//第j个数的第i位是1还是0s[j] = s[j - 1] ^ num;//前缀异或和if (s[j] == 1){num1++;}else{num0++;}//记录第i位0和1的数量}//cout << num1 << " " << num0 << endl;ans += num1 * num0 * (1 << i);//贡献为0和1的段之和和数值贡献的乘积}cout << ans << endl;}
signed main()
{int t = 1;
//    cin >> t;while (t--){solve();}return 0;
}

---

 第5题  挖矿

代码如下：

#include <bits/stdc++.h>
using namespace std;
const int N=1e7+5;//评测用
int r[N]={0},l[N]={0};//两个数组存放正负方向的矿洞
int f=0,res=0;//
int main(){
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++){int pos;cin>>pos;//输入坐标，即矿洞 if(pos>0) r[pos]++;//存放正负方向的矿洞if(pos<0) l[abs(pos)]++;if(!pos) f++;//也要考虑0坐标的矿洞
}
r[0]=l[0]=0;
for(int i=1;i<=m;i++){//移动距离最大为m，在m范围里前缀和，统计m范围里左右两边各自的矿洞r[i]+=r[i-1];l[i]+=l[i-1];
}
for(int i=1;i<=m;i++){//也是在m范围里考虑，计算矿石数目int sum1=r[i];if(m-2*i>0){sum1+=l[m-2*i];//从正坐标可以返回到负坐标的情况，如果返回不了直接等于第一个sum1}int sum2=l[i];if(m-2*i>0){sum2+=r[m-2*i];//从负坐标可以返回到正坐标的情况，如果返回不了直接等于第一个sum2}res=max({res,sum1,sum2});//正确更新res避免每次max被覆盖 
}
cout<<res+f;
return 0;
}

---

片尾

今天我们学习了前缀和和差分思想，希望看完这篇文章能对友友们有所帮助！！！

求点赞收藏加关注！！！

谢谢大家！！！