区间 dp 系列 题解
1.洛谷 P4342 IOI1998 Polygon
我的博客
2.洛谷 P4290 HAOI2008 玩具取名
题意
某人有一套玩具,并想法给玩具命名。首先他选择 W, I, N, G 四个字母中的任意一个字母作为玩具的基本名字。然后他会根据自己的喜好,将名字中任意一个字母用 W, I, N, G 中任意两个字母代替,使得自己的名字能够扩充得很长。
现在,他想请你猜猜某一个很长的名字,最初可能是由哪几个字母变形过来的。
四个整数 W , I , N , G W, I, N, G W,I,N,G,表示每一个字母能由几种两个字母所替代:
-
接下来 W W W 行,每行两个字母,表示
W可以用这两个字母替代。 -
接下来 I I I 行,每行两个字母,表示
I可以用这两个字母替代。 -
接下来 N N N 行,每行两个字母,表示
N可以用这两个字母替代。 -
接下来 G G G 行,每行两个字母,表示
G可以用这两个字母替代。 -
最后一行一个长度不超过 L L L 的字符串。表示这个玩具的名字。
一行字符串,输出该名字可能由哪一个字母变形而得到。(按照 W, I, N, G 的顺序输出)
如果给的名字不能由任何一个字母变形而得到则输出 The name is wrong!。
L ≤ 200 L \leq 200 L≤200, W , I , N , G ≤ 16 W, I, N, G \leq 16 W,I,N,G≤16。
思路
其实就是原字符串中,找其中两个合并成特定的一个字母,问最后能否变成只有一个字母。合并问题,想到用区间 dp。
不妨给 4 4 4 个字母编号: W , I , N , G \rm W,I,N,G W,I,N,G 分别对应 1 , 2 , 3 , 4 1,2,3,4 1,2,3,4。设 f i , j , x f_{i,j,x} fi,j,x 表示区间 [ i , j ] [i,j] [i,j] 的字符,是否可以合并成编号为 x x x 的字符。
考虑转化为子问题:将区间 [ i , j ] [i,j] [i,j] 拆分成 [ i , k ] [i,k] [i,k] 和 [ k + 1 , j ] [k+1,j] [k+1,j],并且分别期望用编号为 p q , p , q pq,p,q pq,p,q 的字母来覆盖(这变量够直观吧)。
如果左右区间都可以被完全替换为期望字符,并且编号为 p q pq pq 的字母可以被两个编号分别为 p , q p,q p,q 的字母并起来替代,那么 f i , j , x = 1 f_{i,j,x}=1 fi,j,x=1。
至于关系就很好处理了。我的代码是懒人写法:
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=203;
ll m[5];
string s;
bool vis[5][5][5],f[N][N][5];//f(i,j,x):区间[i,j]能否替换成字母编号x
ll chg(char c)
{if(c=='W')return 1;if(c=='I')return 2;if(c=='N')return 3;return 4;
}
char print(ll i)
{if(i==1)return 'W';if(i==2)return 'I';if(i==3)return 'N';return 'G';
}
int main()
{ios::sync_with_stdio(0);for(int i=1;i<=4;i++)cin>>m[i];for(int i=1;i<=4;i++){for(int j=1;j<=m[i];j++){string t;cin>>t;vis[i][chg(t[0])][chg(t[1])]=1;}}cin>>s;ll n=s.size();s='*'+s;for(int i=1;i<=n;i++)f[i][i][chg(s[i])]=1;for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++){ll j=i+len-1;for(int k=i;k<j;k++)for(int pq=1;pq<=4;pq++)for(int p=1;p<=4;p++)for(int q=1;q<=4;q++)if(vis[pq][p][q]&&f[i][k][p]&&f[k+1][j][q])f[i][j][pq]=1;}}bool flag=0;for(int pq=1;pq<=4;pq++){if(f[1][n][pq])cout<<print(pq);flag|=f[1][n][pq];}if(!flag)puts("The name is wrong!");return 0;
}
3.CF607B Zuma
题意
Genos \texttt{Genos} Genos 最近在他的手机上下载了祖玛游戏。在祖玛游戏里,存在 n n n 个一行的宝石,第 i i i 个宝石的颜色是 a i a_i ai。这个游戏的目标是尽快的消灭一行中所有的宝石。
在一秒钟, Genos \texttt{Genos} Genos 能很快的挑选出这些有颜色的宝石中的一个回文的、连续的子串,并将这个子串移除。每当一个子串被删除后,剩余的宝石将连接在一起,形成一个新的行列。
求把整个宝石串都移除的最短时间。
1 ≤ n ≤ 500 1 \le n \le 500 1≤n≤500。
思路
合并就考虑区间 dp,设 f i , j f_{i,j} fi,j 表示区间 [ i , j ] [i,j] [i,j] 能否被完全消除,那么有几个明显的结论:
- f i , i = 1 f_{i,i}=1 fi,i=1
- f i , i + 1 = { 1 , a i = a i + 1 2 , a i ≠ a i + 1 f_{i,i+1}=\left\{\begin{matrix} 1,a_i=a_{i+1}\\ 2,a_i\neq a_{i+1} \end{matrix}\right. fi,i+1={1,ai=ai+12,ai=ai+1
- f i , j = f i + 1 , j − 1 , a i = a j f_{i,j}=f_{i+1,j-1},a_i=a_j fi,j=fi+1,j−1,ai=aj
前两点用于初始化。第三点作为特殊情况;对于朴素情况,枚举断点 k ∈ [ i , j ) k\in[i,j) k∈[i,j) 就好:
f i , j = min { f i , k + f k + 1 , j } f_{i,j}=\min\{f_{i,k}+f_{k+1,j}\} fi,j=min{fi,k+fk+1,j}
只需讨论区间长度为 3 3 3 的就好了。
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=502,inf=0x3f3f3f3f;
ll n,a[N];
ll f[N][N];//f(i,j):区间[i,j]全部消除的最短时间
bool palin(ll l,ll r)
{for(int i=l,j=r;i<=j;i++,j--)if(a[i]!=a[j])return 0;return 1;
}
int main()
{scanf("%lld",&n);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);for(int i=1;i<=n;i++){f[i][i]=1;if(a[i]==a[i+1])f[i][i+1]=1;else f[i][i+1]=2;for(int j=i+2;j<=n;j++)f[i][j]=inf;}for(int len=3;len<=n;len++){for(int i=1;i+len-1<=n;i++){ll j=i+len-1;if(a[i]==a[j])f[i][j]=f[i+1][j-1];for(int k=i;k<j;k++)f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]);}}printf("%lld",f[1][n]);return 0;
}
4.洛谷 P5189 SP6340 Zuma
这道题就是平时玩的祖玛游戏的规则了。
我的博客
相关文章:

区间 dp 系列 题解
1.洛谷 P4342 IOI1998 Polygon 我的博客 2.洛谷 P4290 HAOI2008 玩具取名 题意 某人有一套玩具,并想法给玩具命名。首先他选择 W, I, N, G 四个字母中的任意一个字母作为玩具的基本名字。然后他会根据自己的喜好,将名字中任意一个字母用 W, I, N, G …...

Spring Boot 自动加载流程详解
前言 Spring Boot 是一个基于约定优于配置理念的框架,它通过自动加载机制大大简化了开发者的配置工作。本文将深入探讨 Spring Boot 的自动加载流程,并结合源码和 Mermaid 图表进行详细解析。 一、Spring Boot 自动加载的核心机制 Spring Boot 的自动加…...

《从底层逻辑剖析:分布式软总线与传统计算机硬件总线的深度对话》
在科技飞速发展的当下,我们正见证着计算机技术领域的深刻变革。计算机总线作为信息传输的关键枢纽,其发展历程承载着技术演进的脉络。从传统计算机硬件总线到如今备受瞩目的分布式软总线,每一次的变革都为计算机系统性能与应用拓展带来了质的…...
Fay 数字人部署环境需求
D:\ai\Fay>python main.py pygame 2.6.1 (SDL 2.28.4, Python 3.11.9) Hello from the pygame community. https://www.pygame.org/contribute.html [2025-04-11 00:10:16.7][系统] 注册命令... [2025-04-11 00:10:16.8][系统] restart 重启服务 [2025-04-11 00:10:16.8][…...

python:all列表
1.all列表的说明: 当模块中有__all__变量时,当使用from xxx import *时,只能导入这个列表中的元素。 2.具体的例子: 1.先创建一个模块my_mod,在列表__all__中分别写入第一次只写入test1,第二次写入test1、test2两个…...

基于 SpringBoot 的校园论坛系统
收藏关注不迷路!! 🌟文末获取源码数据库🌟 感兴趣的可以先收藏起来,还有大家在毕设选题(免费咨询指导选题),项目以及论文编写等相关问题都可以给我留言咨询,希望帮助更多…...

2025 跨平台技术如何选:KMP 与 Flutter 的核心差异
前言 在移动开发的演进历程中,跨平台技术始终是一个充满争议却无法回避的话题。从早期的 React Native 到如今的 Kotlin Multiplatform(KMP)和 Flutter,开发者们始终在代码复用与原生体验之间寻找平衡。本文我们从技术实现、性能…...

深度学习总结(6)
随机梯度下降 给定一个可微函数,理论上可以用解析法找到它的最小值:函数的最小值就是导数为0的点,因此只需找到所有导数为0的点,然后比较函数在其中哪个点的取值最小。将这一方法应用于神经网络,就是用解析法求出损失…...

SpringBoot实战1
SpringBoot实战1 一、开发环境,环境搭建-----创建项目 通过传统的Maven工程进行创建SpringBoot项目 (1)导入SpringBoot项目开发所需要的依赖 一个父依赖:(工件ID为:spring-boot-starter-parent…...
)
深度学习实战:从零构建图像分类API(Flask/FastAPI版)
引言:AI时代的图像分类需求 在智能时代,图像分类技术已渗透到医疗影像分析、自动驾驶、工业质检等各个领域。作为开发者,掌握如何将深度学习模型封装为API服务,是实现技术落地的关键一步。本文将手把手教你使用Python生态中的Fla…...

【Linux】39.一个基础的HTTP Web服务器
文章目录 1. 实现一个基础的HTTP Web服务器1.1 功能实现:1.2 Log.hpp-日志记录器1.3 HttpServer.hpp-网页服务器1.4 Socket.hpp-网络通信器1.5 HttpServer.cc-服务器启动器 1. 实现一个基础的HTTP Web服务器 1.1 功能实现: 总体功能: 提供We…...

阿里云域名证书自动更新acme.sh
因为阿里云的免费证书只有三个月的有效期,每次更换都比较繁琐,所以找到了 acme.sh,还有一种 certbot 我没有去了解,就直接使用了 acme.sh 来更新证书,acme.sh 的主要特点就是: 支持多种 DNS 服务商自动化续…...

大数据Hadoop(MapReduce)
MapReduce概述 MapReduce定义 MapReduce是一个分布式运算程序的编程框架,是用户开发“基于Hadoop的数据分析应用”的核心框架。 MapReduce核心功能是将用户编写的业务逻辑代码和自带默认组件整合成一个完整的分布式运算程序,并发运行在一个Hadoop集群上…...

图灵逆向——题十七-字体加密
十七题是一个很经典的字体加密案例,很适合新手入门~ 目录列表 过程分析代码实现 过程分析 打开开发者工具直接看请求,发现它请求的没有加密参数,以为万事大吉的你迫不及待的点击了响应,然后就会发现依托。。。 返回的数据中字体…...
蓝桥杯准备(需要写的基础))
(自用)蓝桥杯准备(需要写的基础)
要写的文件 led_app lcd_app key_app adc_app usart_app scheduler LHF_SYS一、外设引脚配置 1. 按键引脚 按键引脚配置如下: B1:PB0B2:PB1B3:PB2B4:PA0 2. LCD引脚 LCD引脚配置如下: GPIO_Pin_9 /* …...

系统与网络安全------网络通信原理(5)
资料整理于网络资料、书本资料、AI,仅供个人学习参考。 传输层解析 传输层 传输层的作用 IP层提供点到点的连接传输层提供端到端的连接 端口到端口的连接(不同端口号,代表不同的应用程序) TCP协议概述 TCP(Transm…...

minio提供nfs服务
minio提供nfs服务 挂载minio为本地目录配置开机自动挂载方法1: 使用supervisor实现开机自动挂载方法2: 服务单元实现开机自动挂载minio为本地目录---失败调试 配置NFS服务端 挂载minio为本地目录 使用 Minio 作为后端存储,并通过 NFS 为客户端提供访问,…...
)
vue2添加背景水印-手动实现(无组件模式)
1. App.vue <template><div id="app" class="app"><router-view></router-view></div> </template><script> export default {mounted() {this.updateWatermark();// 监听路由变化this.$router.afterEach(() =…...

嵌入式---加速度计
一、基本概念与定义 定义 加速度计(Accelerometer)是一种测量物体加速度(线性加速度或振动加速度)的传感器,可检测物体运动状态、振动幅度、倾斜角度等,输出与加速度成比例的电信号(模拟或数字信…...
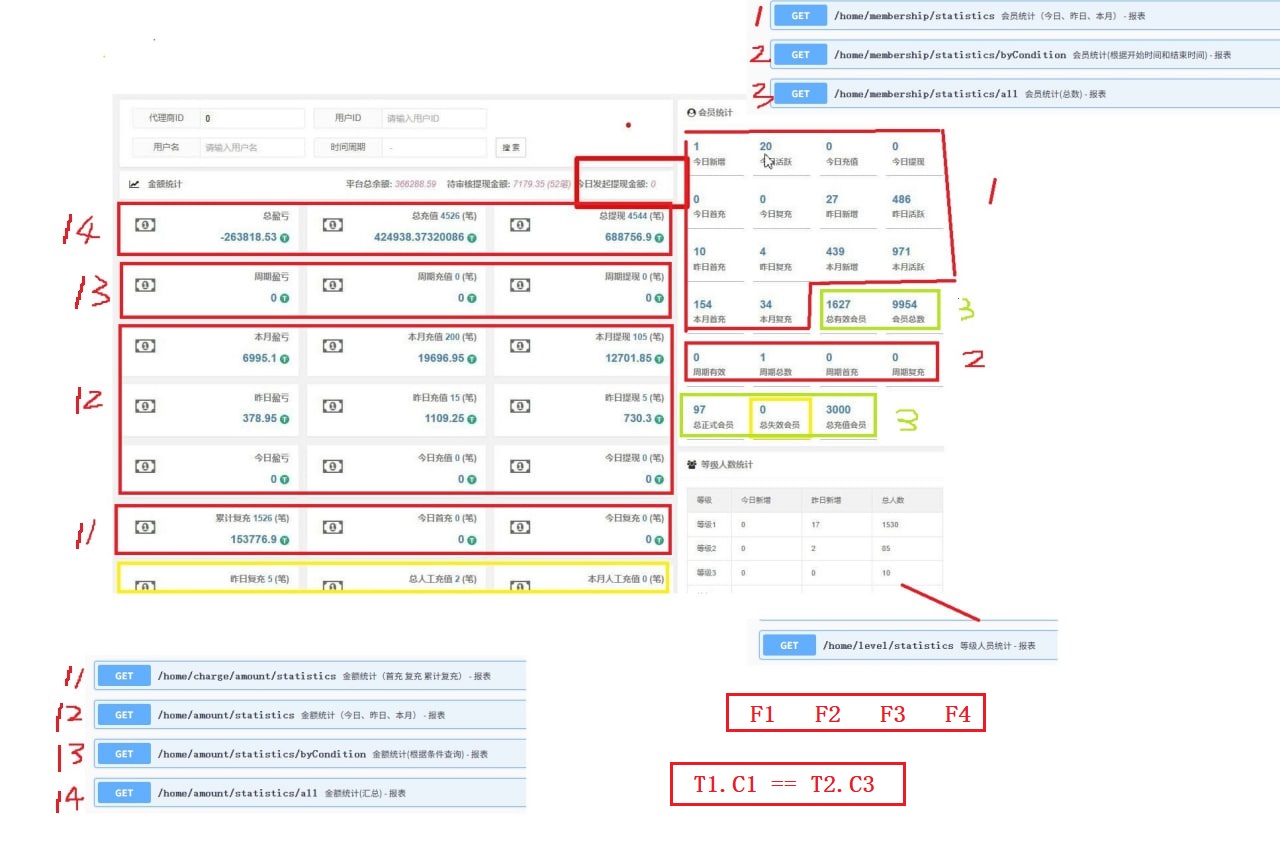
swagger + Document
swagger 虽然有了api接口,对于复杂接口返回值说明,文档还是不能少。如果是一个人做的还简单一点,现在都搞前后端分离,谁知道你要取那个值呢...

【Git】--- 多人协作实战场景
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏: Git 前面我们学习了Git的所有本地仓库的相关操作:git基本操作,分支理解,版本回退,冲突解决等等。同时我们还理解了远端仓库在开发的作用以及相关操作push…...

Higress: 阿里巴巴高性能云原生API网关详解
一、Higress概述 Higress是阿里巴巴开源的一款基于云原生技术构建的高性能API网关,专为Kubernetes和微服务架构设计。它集成了Ingress控制器、微服务网关和API网关功能于一体,支持多种协议和丰富的流量管理能力。 发展历程 Higress 从最初社区的 Isti…...

常见的 set 选项与空变量检查
在编写 Bash 脚本时,使用 set 命令中的一些选项可以帮助我们在脚本执行过程中及时捕获错误和潜在问题,避免脚本在出错时继续执行,提高脚本的可靠性和健壮性。 set -e:遇到错误就停 set -e 的作用是:一旦脚本中的某个…...

leetcode 377. Combination Sum IV
这道题也是完全背包问题。这道题和第518题几乎一摸一样,所不同的是,第518题要求的是组合数,而第377题要求的是排列数。虽然本题题目描述中说求的是组合数,但从例子1中(1,1,2)和&…...

VM——相机拍照失败
1、问题:相机频闪触发,在MVS中正常出图,在VM中出现拍照失败 2、解决: 1、首先排查网络设置(巨帧是否设置) 2、电脑的所有防火墙是否关闭 3、在MVS中恢复相机的设置参数为默认参数,删除VM中的全…...

初识Redis · 简单理解Redis
目录 前言: 分布式系统 开源节流 认识Redis 负载均衡 缓存 微服务 前言: 本文只是作为Redis的一篇杂谈,简单理解一下Redis为什么要存在,以及它能做到和它不能做到的事儿,简单提及一下它对应的优势有什么&#…...

目标检测YOLO实战应用案例100讲- 基于卷积神经网络的小目标检测算法研究与应用
目录 知识储备 基于改进YOLOv5的小目标检测算法 一、环境配置(Python 3.8+) 二、核心代码实现 1. 改进模型定义(models/yolov5s_tiny.py ) 2. 小目标数据增强(datasets/tiny_aug.py ) 3. 训练脚本(train.py ) 三、关键改进点说明 四、实验配置建议 前言 传统…...

自动驾驶时间同步
主要包含两个大的概念:时间系统间的时间同步与传感器数据间的时间同步 1. 时间系统间的时间同步 概念: 自动驾驶域控一般由多个芯片与多种类型的传感器组成,如:MCU SoC Camera Lidar Radar USS GNSS,其中 MCU…...

项目进度延误的十大原因及应对方案
项目进度延误主要源于以下十大原因:目标不明确、需求频繁变更、资源配置不足或不合理、沟通不畅、风险管理不足、缺乏有效的项目监控、技术难题未及时解决、团队协作效率低下、决策链过长、外部因素影响。其中,需求频繁变更是导致延误的关键因素之一&…...

消息队列(IPC技术)
目录 一、Linux 中主要的进程间通信方式如下: 二、消息队列函数 (1)msgget函数 功能概述 函数原型 参数解释 返回值 示例 结果 问题 (2) msgsnd函数 功能概述 函数原型 参数说明 返回值 示例 结果 (3࿰…...
