【C++游戏引擎开发】第9篇:数学计算库GLM(线性代数)、CGAL(几何计算)的安装与使用指南
写在前面
两天都没手搓实现可用的凸包生成算法相关的代码,自觉无法手搓相关数学库,遂改为使用成熟数学库。
一、GLM库安装与介绍
1.1 vcpkg安装GLM
跨平台C++包管理利器vcpkg完全指南
在PowerShell中执行命令:
vcpkg install glm# 集成到系统目录,只需要执行一次,以前执行过就无需重复执行
vcpkg integrate install
1.2 GLM库基础数学对象
| 类型 | 描述 | 示例 |
|---|---|---|
| vec2/3/4 | 2/3/4维浮点向量 | vec3 position(1,2,3); |
| mat2/3/4 | 2x2、3x3、4x4浮点矩阵 | mat4 view = lookAt(…); |
| quat | 四元数(旋转表示) | quat rotation = angleAxis(…); |
| dvec*/dmat* | 双精度向量/矩阵 | dmat4 highPrecisionMat; |
1.3 GLM库使用示例代码(矩阵计算、四元数计算等)
// main.cpp
// main.cpp
#include <iostream>
#include <limits>#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>#define GLM_ENABLE_EXPERIMENTAL
#include <glm/gtx/string_cast.hpp> // 用于矩阵字符串输出
#include <glm/gtx/quaternion.hpp>// 打印GLM矩阵(带标签)
template<typename T>
void print_matrix(const std::string& name, const T& mat) {std::cout << name << ":\n" << glm::to_string(mat) << "\n\n";
}// 定义OBB结构体
struct OBB {glm::vec3 center; // 包围盒中心glm::vec3 extents; // 包围盒半长(x, y, z方向的半径)glm::mat3 rotation; // 旋转矩阵(局部到世界坐标的变换)
};// 射线与OBB相交检测(返回相交距离,未相交返回-1)
float rayOBBIntersection(const glm::vec3& rayOrigin,const glm::vec3& rayDir,const OBB& obb,float maxDistance = std::numeric_limits<float>::max()
) {// 将射线转换到OBB局部空间glm::mat3 invRotation = glm::transpose(obb.rotation); // 旋转的逆矩阵glm::vec3 localOrigin = invRotation * (rayOrigin - obb.center);glm::vec3 localDir = invRotation * rayDir;// 射线与AABB相交检测(在局部空间)float tMin = 0.0f;float tMax = maxDistance;// 分别检查每个轴for (int i = 0; i < 3; ++i) {float axisMin = -obb.extents[i] - localOrigin[i];float axisMax = obb.extents[i] - localOrigin[i];if (std::abs(localDir[i]) < 1e-6) { // 射线与轴平行if (localOrigin[i] < -obb.extents[i] || localOrigin[i] > obb.extents[i])return -1.0f;}else {float invDir = 1.0f / localDir[i];float t1 = axisMin * invDir;float t2 = axisMax * invDir;if (t1 > t2) std::swap(t1, t2);tMin = std::max(tMin, t1);tMax = std::min(tMax, t2);if (tMin > tMax) return -1.0f;}}return tMin;
}// 在main函数中添加测试代码
void testRayOBB() {std::cout << "===== OBB射线检测测试 =====" << std::endl;// 创建一个旋转45度的OBBOBB obb;obb.center = glm::vec3(2.0f, 0.0f, 0.0f);obb.extents = glm::vec3(1.0f, 0.5f, 0.5f);obb.rotation = glm::mat3_cast(glm::angleAxis(glm::radians(45.0f), glm::vec3(0, 0, 1)));// 测试射线1:应相交glm::vec3 rayOrigin1(0.0f, 0.0f, 0.0f);glm::vec3 rayDir1 = glm::normalize(glm::vec3(1.0f, 0.0f, 0.0f));float t1 = rayOBBIntersection(rayOrigin1, rayDir1, obb);std::cout << "射线1结果: " << (t1 >= 0 ? "命中,距离=" + std::to_string(t1) : "未命中") << std::endl;// 测试射线2:应不相交glm::vec3 rayOrigin2(0.0f, 2.0f, 0.0f);glm::vec3 rayDir2 = glm::normalize(glm::vec3(1.0f, 0.0f, 0.0f));float t2 = rayOBBIntersection(rayOrigin2, rayDir2, obb);std::cout << "射线2结果: " << (t2 >= 0 ? "命中,距离=" + std::to_string(t2) : "未命中") << std::endl;// 测试射线3:从内部发射glm::vec3 rayOrigin3 = obb.center;glm::vec3 rayDir3 = glm::normalize(glm::vec3(1.0f, 0.0f, 0.0f));float t3 = rayOBBIntersection(rayOrigin3, rayDir3, obb);std::cout << "射线3结果: " << (t3 >= 0 ? "命中,距离=" + std::to_string(t3) : "未命中") << std::endl;std::cout << "\n";
}int main() {// ======================// 1. 矩阵基本操作// ======================// 创建两个4x4矩阵glm::mat4 A(1.0f); // 单位矩阵glm::mat4 B = glm::translate(glm::mat4(1.0f), glm::vec3(2, 3, 4)); // 平移矩阵// 矩阵加法glm::mat4 C = A + B;print_matrix("Matrix A (Identity)", A);print_matrix("Matrix B (Translation)", B);print_matrix("Matrix C = A + B", C);// 矩阵减法glm::mat4 D = B - A;print_matrix("Matrix D = B - A", D);// 矩阵乘法(组合变换)glm::mat4 trans = glm::translate(glm::mat4(1.0f), glm::vec3(1, 0, 0));glm::mat4 scale = glm::scale(glm::mat4(1.0f), glm::vec3(2, 2, 2));glm::mat4 combined = trans * scale; // 先缩放后平移print_matrix("Combined Matrix (Scale then Translate)", combined);// ======================// 2. 矩阵求逆// ======================glm::mat4 invB = glm::inverse(B);print_matrix("Inverse of Matrix B", invB);// 验证B * invB ≈ Identityglm::mat4 identityCheck = B * invB;print_matrix("B * invB (Should be Identity)", identityCheck);// ======================// 3. 四元数操作// ======================// 创建绕Y轴旋转45度的四元数glm::quat q1 = glm::angleAxis(glm::radians(45.0f), glm::vec3(0, 1, 0));// 创建绕X轴旋转30度的四元数glm::quat q2 = glm::angleAxis(glm::radians(30.0f), glm::vec3(1, 0, 0));// 四元数插值(球面线性插值)glm::quat slerped = glm::slerp(q1, q2, 0.5f);// 将四元数转换为旋转矩阵glm::mat4 rotMat = glm::mat4_cast(slerped);print_matrix("Rotation Matrix from Slerped Quaternion", rotMat);// 使用四元数旋转向量glm::vec3 originalVec(1, 0, 0);glm::vec3 rotatedVec = slerped * originalVec;std::cout << "Original Vector: (" << originalVec.x << ", " << originalVec.y << ", " << originalVec.z << ")\n";std::cout << "Rotated Vector: (" << rotatedVec.x << ", " << rotatedVec.y << ", " << rotatedVec.z << ")\n\n";testRayOBB();return 0;
}
二、CGAL库安装与使用
2.1 vcpkg安装CGAL库
在PowerShell中执行命令:
vcpkg install cgal
注:安装过程较长,很慢。
2.2 CGAL示例代码(凸包生成、三角剖分)
#include <iostream>
#include <vector>
#include <iterator> // 添加iterator头文件
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/convex_hull_2.h>
#include <CGAL/convex_hull_3.h>
#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/Delaunay_triangulation_3.h>
#include <CGAL/point_generators_2.h>
#include <CGAL/point_generators_3.h>
#include <CGAL/Polyhedron_3.h> // 添加Polyhedron_3头文件using namespace std;// 定义内核类型(快速浮点数计算)
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef K::Point_2 Point_2;
typedef K::Point_3 Point_3;
typedef CGAL::Polyhedron_3<K> Polyhedron_3; // 定义多面体类型//------- 二维凸包测试 -------
void test_2d_convex_hull() {cout << "===== 二维凸包测试 =====" << endl;// 生成100个随机二维点(坐标范围[0, 100))CGAL::Random_points_in_square_2<Point_2> gen(50.0);vector<Point_2> points;const int NUM_POINTS = 20;CGAL::cpp11::copy_n(gen, NUM_POINTS, back_inserter(points));// 计算凸包vector<Point_2> hull;CGAL::convex_hull_2(points.begin(), points.end(), back_inserter(hull));// 输出结果cout << "原始点集(" << points.size() << "):" << endl;for (const auto& p : points)cout << "(" << p.x() << ", " << p.y() << ") ";cout << "\n\n凸包顶点(" << hull.size() << "):" << endl;for (const auto& p : hull)cout << "(" << p.x() << ", " << p.y() << ") ";cout << "\n\n";
}//------- 三维凸包测试 -------
void test_3d_convex_hull() {cout << "===== 三维凸包测试 =====" << endl;// 生成20个随机三维点CGAL::Random_points_in_sphere_3<Point_3> gen(50.0);vector<Point_3> points;const int NUM_POINTS = 20;copy_n(gen, NUM_POINTS, back_inserter(points)); // 移除非必要的CGAL::cpp11::// 计算三维凸包Polyhedron_3 hull;CGAL::convex_hull_3(points.begin(), points.end(), hull);// 输出结果cout << "三维凸包面数: " << std::distance(hull.facets_begin(), hull.facets_end()) << endl;int faceCount = 0;for (auto face = hull.facets_begin(); face != hull.facets_end(); ++face, ++faceCount) {cout << "面 " << faceCount << ": ";auto he = face->halfedge();for (int i = 0; i < 3; ++i) { // 假设所有面都是三角形const auto& p = he->vertex()->point();cout << "(" << p.x() << ", " << p.y() << ", " << p.z() << ") ";he = he->next();}cout << endl;}cout << "\n";
}
//------- 二维Delaunay三角剖分测试 -------
void test_2d_delaunay() {cout << "===== 二维Delaunay三角剖分测试 =====" << endl;// 生成100个随机二维点CGAL::Random_points_in_square_2<Point_2> gen(50.0);vector<Point_2> points;const int NUM_POINTS = 10;copy_n(gen, NUM_POINTS, back_inserter(points)); // 移除非必要的CGAL::cpp11::// 构建Delaunay三角网CGAL::Delaunay_triangulation_2<K> dt;dt.insert(points.begin(), points.end());// 输出统计信息cout << "顶点数: " << dt.number_of_vertices() << endl;cout << "面数: " << dt.number_of_faces() << endl;// 遍历所有边(正确方式)cout << "\n边列表:" << endl;for (auto edge = dt.finite_edges_begin(); edge != dt.finite_edges_end(); ++edge) {auto segment = dt.segment(*edge); // 直接获取边对应的线段cout << "(" << segment.source().x() << ", " << segment.source().y() << ") - "<< "(" << segment.target().x() << ", " << segment.target().y() << ")\n";}cout << "\n";
}//------- 三维Delaunay三角剖分测试 -------
void test_3d_delaunay() {cout << "===== 三维Delaunay三角剖分测试 =====" << endl;// 生成10个随机三维点CGAL::Random_points_in_sphere_3<Point_3> gen(50.0);vector<Point_3> points;const int NUM_POINTS = 10;CGAL::cpp11::copy_n(gen, NUM_POINTS, back_inserter(points));// 构建三维Delaunay三角网CGAL::Delaunay_triangulation_3<K> dt;dt.insert(points.begin(), points.end());// 输出统计信息cout << "顶点数: " << dt.number_of_vertices() << endl;cout << "边数: " << dt.number_of_edges() << endl;cout << "面数: " << dt.number_of_facets() << endl;cout << "四面体数: " << dt.number_of_cells() << endl;// 遍历所有四面体cout << "\n四面体列表:" << endl;for (auto cell = dt.finite_cells_begin(); cell != dt.finite_cells_end(); ++cell) {const Point_3& p0 = cell->vertex(0)->point();const Point_3& p1 = cell->vertex(1)->point();const Point_3& p2 = cell->vertex(2)->point();const Point_3& p3 = cell->vertex(3)->point();cout << "四面体: \n";cout << " (" << p0.x() << ", " << p0.y() << ", " << p0.z() << ")\n"<< " (" << p1.x() << ", " << p1.y() << ", " << p1.z() << ")\n"<< " (" << p2.x() << ", " << p2.y() << ", " << p2.z() << ")\n"<< " (" << p3.x() << ", " << p3.y() << ", " << p3.z() << ")\n";}cout << "\n";
}int main() {// 运行各测试用例test_2d_convex_hull();test_3d_convex_hull();test_2d_delaunay();test_3d_delaunay();return 0;
}
相关文章:
、CGAL(几何计算)的安装与使用指南)
【C++游戏引擎开发】第9篇:数学计算库GLM(线性代数)、CGAL(几何计算)的安装与使用指南
写在前面 两天都没手搓实现可用的凸包生成算法相关的代码,自觉无法手搓相关数学库,遂改为使用成熟数学库。 一、GLM库安装与介绍 1.1 vcpkg安装GLM 跨平台C包管理利器vcpkg完全指南 在PowerShell中执行命令: vcpkg install glm# 集成到系…...
)
408 计算机网络 知识点记忆(8)
前言 本文基于王道考研课程与湖科大计算机网络课程教学内容,系统梳理核心知识记忆点和框架,既为个人复习沉淀思考,亦希望能与同行者互助共进。(PS:后续将持续迭代优化细节) 往期内容 408 计算机网络 知识…...

基于Python脚本实现Flink on YARN任务批量触发Savepoint的实践指南
基于Python脚本实现Flink on YARN任务批量触发Savepoint的实践指南 一、背景与价值 在流计算生产环境中,Flink on YARN的部署方式凭借其资源管理优势被广泛采用。Savepoint作为Flink任务状态的一致性快照,承载着故障恢复、版本升级、作业暂停等重要场景…...

我可能用到的网站和软件
我可能用到的网站和软件 程序员交流的网站代码管理工具前端组件库前端框架在线工具人工智能问答工具学习的网站Windows系统电脑的常用工具 程序员交流的网站 csdn博客博客园 - 开发者的网上家园InfoQ - 软件开发及相关领域-极客邦掘金 (juejin.cn) 代码管理工具 GitHub 有时…...

FPGA状态机设计:流水灯实现、Modelsim仿真、HDLBits练习
一、状态机思想 1.概念 状态机(Finite State Machine, FSM)是计算机科学和工程领域中的一种抽象模型,用于描述系统在不同状态之间的转换逻辑。其核心思想是将复杂的行为拆解为有限的状态,并通过事件触发状态间的转移。 2.状态机…...

2024年第十五届蓝桥杯CC++大学A组--成绩统计
2024年第十五届蓝桥杯C&C大学A组--成绩统计 题目: 动态规划, 对于该题,考虑动态规划解法,先取前k个人的成绩计算其方差,并将成绩记录在数组中,记录当前均值,设小蓝已检查前i-1个人的成绩&…...
——ListBox控件详解)
WinForm真入门(13)——ListBox控件详解
WinForm ListBox 详解与案例 一、核心概念 ListBox 是 Windows 窗体中用于展示可滚动列表项的控件,支持单选或多选操作,适用于需要用户从固定数据集中选择一项或多项的场景。 二、核心属性 属性说明Items管理列表项的集合,支持动…...

Kotlin 学习-集合
/*** kotlin 集合* List:是一个有序列表,可通过索引(下标)访问元素。元素可以在list中出现多次、元素可重复* Set:是元素唯一的集合。一般来说 set中的元素顺序并不重要、无序集合* Map:(字典)是一组键值对。键是唯一的…...

解决java使用easyexcel填充模版后,高度不一致问题
自定义工具,可以通过获取上一行行高设置后面所以行的高度 package org.springblade.modules.api.utils;import com.alibaba.excel.write.handler.RowWriteHandler; import com.alibaba.excel.write.metadata.holder.WriteSheetHolder; import com.alibaba.excel.wr…...

数据结构与算法之ACM Fellow-算法4.3 最小生成树
数据结构与算法之ACM Fellow-算法4.3 最小生成树 加权图 是一种为每条边关联一个 权值 或是 成本 的图模型。这种图能够自然地表示许多应用。在一幅航空图中,边表示航线,权值则可以表示距离或是费用。在一幅电路图中,边表示导线,…...

使用POCO库进行ZIP压缩和解压
使用POCO库进行ZIP压缩和解压 POCO C Libraries提供了一个ZIP模块,可以方便地进行文件和数据流的压缩与解压操作。下面我将介绍如何使用POCO的ZIP模块进行这些操作。 1. 基本ZIP文件操作 压缩文件/目录到ZIP #include <Poco/Zip/Compress.h> #include <…...

自动驾驶的未来:多模态感知融合技术最新进展
作为自动驾驶领域的专业人士,我很高兴与大家分享关于多模态感知融合技术的前沿研究和实践经验。在迅速发展的自动驾驶领域,多模态感知融合已成为提升系统性能的关键技术。本文将深入探讨基于摄像头和激光雷达的多模态感知融合技术,重点关注最…...

亮相2025全球分布式云大会,火山引擎边缘云落地AI新场景
4 月 9 日,2025 全球分布式云大会暨 AI 基础设施大会在深圳成功举办,火山引擎边缘云产品解决方案高级总监沈建发出席并以《智启边缘,畅想未来:边缘计算新场景落地与 Al 趋势新畅想》为主题,分享了边缘计算在 AI 技术趋…...

XCode集成第三方framework步骤
一、添加 .framework 文件到项目 拖拽或手动添加 在Xcode中,直接将 .framework 文件拖入项目导航器的目标文件夹中, 确保 .framework 文件被复制到项目目录内(非外部路径)。或通过菜单操作: General → Frameworks, Libra…...
无损分区管理,硬盘管理的“瑞士军刀”!
打工人们你们好!这里是摸鱼 特供版~ 今天给大家带来一款简单易用、功能强大的无损分区软件——分区助手技术员版,让你的硬盘管理变得轻松又高效! 推荐指数:★★★★★ 软件简介 分区助手技术员版是一款功能强大的硬盘分区工具&…...

VS Code下开发FPGA——FPGA开发体验提升__下
上一篇:IntelliJ IDEA下开发FPGA-CSDN博客 Type:Quartus 一、安装插件 在应用商店先安装Digtal IDE插件 安装后,把其他相关的Verilog插件禁用,避免可能的冲突。重启后,可能会弹出下面提示 这是插件默认要求的工具链&a…...

ffmpeg播放音视频流程
文章目录 🎬 FFmpeg 解码播放流程概览(以音视频文件为例)1️⃣ 创建结构体2️⃣ 打开音视频文件3️⃣ 查找解码器并打开解码器4️⃣ 循环读取数据包(Packet)5️⃣ 解码成帧(Frame)6️⃣ 播放 / …...

SpringCloud微服务: 分布式架构实战
# SpringCloud微服务: 分布式架构实战 第一章:理解SpringCloud微服务架构 什么是SpringCloud微服务架构? 在当今互联网应用开发中,微服务架构已经成为业界的主流趋势。SpringCloud是一个基于Spring Boot的快速开发微服务架构的工具࿰…...

AI预测3D新模型百十个定位预测+胆码预测+去和尾2025年4月11日第49弹
从今天开始,咱们还是暂时基于旧的模型进行预测,好了,废话不多说,按照老办法,重点8-9码定位,配合三胆下1或下2,杀1-2个和尾,再杀6-8个和值,可以做到100-300注左右。 (1)定…...

Spring其它知识点
33.Spring 源码用到了哪些设计模式? 工厂模式:通过BeanFactory或者ApplicationContext创建Bean对象。BeanFactory是延迟注入,使用到Bean的时候才注入。ApplicationContext是在容器启动时,一次性创建所有的Bean。单例模型…...

【models】Transformer 之 各种 Attention 原理和实现
Transformer 之 各种 Attention 原理和实现 本文将介绍Transformer 中常见的Attention的原理和实现,其中包括: Self Attention、Spatial Attention、Temporal Attention、Cross Attention、Grouped Attention、Tensor Product Attention、FlashAttentio…...

C++ 学习资源整理
awesome-cpp(C 资源大全) 🔗 https://github.com/fffaraz/awesome-cpp 收集了各种 C 库、框架、教程和示例代码。 CPlusPlusThings(C 基础知识整理) 🔗 https://github.com/Light-City/CPlusPlusThings 包…...

opengrok搭建与配置
前提条件 需要配置好docker与docker-compose环境 1.代码准备 mkdir -p /data/opengrok/{etc,src,data} cd /data/opengrok/src/ # 克隆一个测试项目 git clone https://git.kernel.org/pub/scm/linux/kernel/git/stable/linux-stable.git 2.创建docker-compose.yml文件&…...

老硬件也能运行的Win11 IoT LTSC (OEM)物联网版
#记录工作 Windows 11 IoT Enterprise LTSC 2024 属于物联网相关的版本。 Windows 11 IoT Enterprise 是为物联网设备和场景设计的操作系统版本。它通常针对特定的工业控制、智能设备等物联网应用进行了优化和定制,以满足这些领域对稳定性、安全性和长期支持的需求…...

JavaScript 代码混淆与反混淆技术详解
一、代码混淆:让别人看不懂你的代码 混淆技术就是一种“代码伪装术”,目的是让别人很难看懂你的代码逻辑,从而保护你的核心算法或敏感信息。 1. 变量名压缩 原理:把变量名改成乱码,比如把calculatePrice改成a&#…...

数据库守护神-WAL机制
什么是WAL机制? WAL(Write-Ahead Logging,预写日志)是一种保证数据库操作原子性和持久性的核心机制。其核心原则可概括为: 任何数据修改操作,必须在对应的日志记录持久化到磁盘之后,才能将实际…...
Git开发
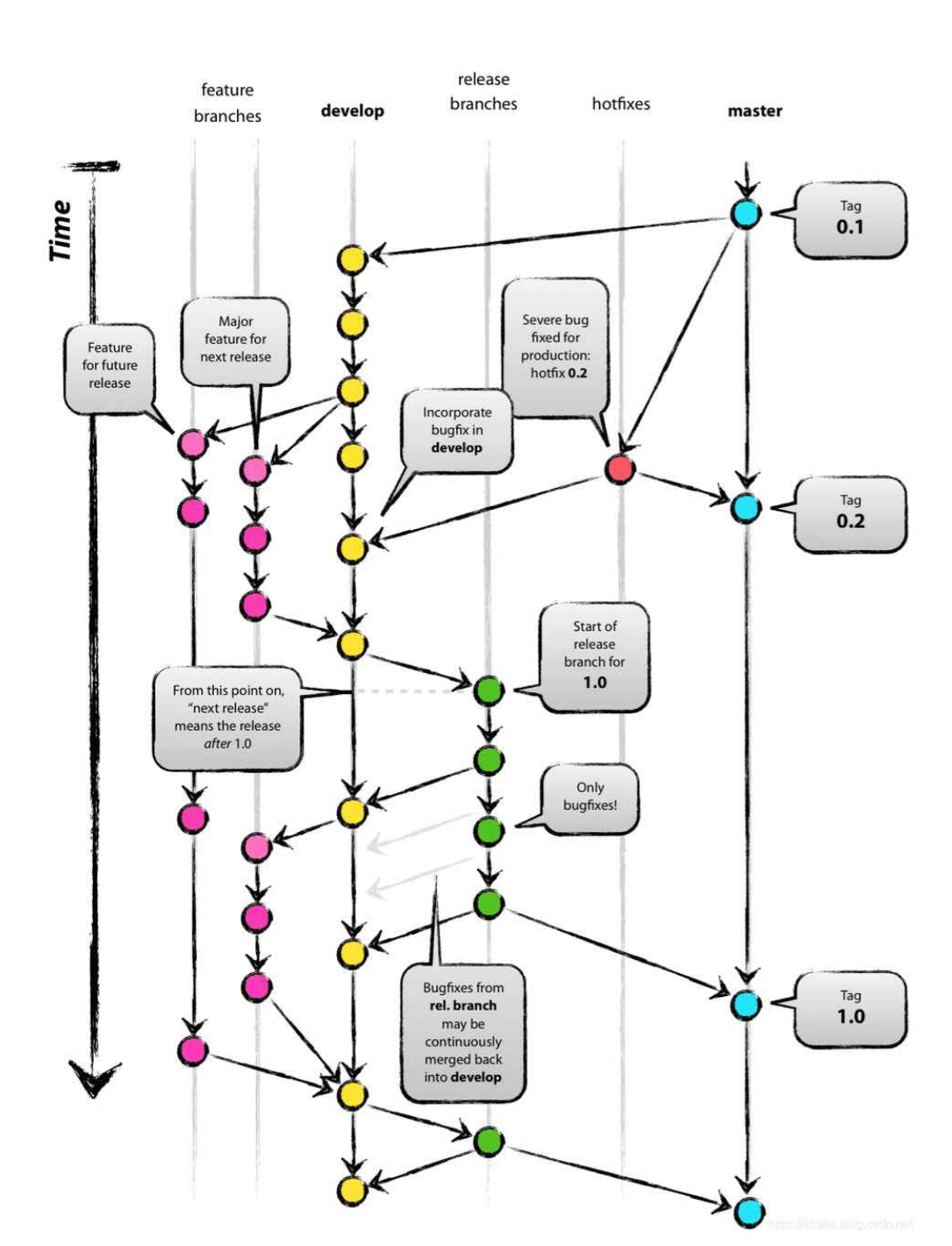
目录 Linux下Git安装Git基本指令分支管理远程仓库与本地仓库标签管理多人协作同一分支下不同分支下 企业级开发模型 -- git flow 模型 在现实中,当我们完成一个文档的初稿后,后面可能还需要对初稿进行反复修改,从而形成不同版本的文档。显然&…...

verilog有符号数的乘法
无符号整数的乘法 1、单周期乘法器( 无符号整数 ) 对于低速要求的乘法器,可以简单的使用 * 实现。 module Mult(input wire [7:0] multiplicand ,input wire [7:0] multipliter ,output wire [7:0] product);as…...

【蓝桥杯】动态规划:背包问题
这篇文章主要记录动态规划方面的学习。 动态规划的核心思想: 把大问题分解成小问题,记住小问题的解,避免重复计算。 动态规划(DP)的三大特点: ①最优子结构:大问题的最优解可以由小问题的最优解推导出来 ②重叠子问题:在求解过程中会反复遇到相同的小问题 ③无后效…...

DevDocs:抓取并整理技术文档的MCP服务
GitHub:https://github.com/cyberagiinc/DevDocs 更多AI开源软件:发现分享好用的AI工具、AI开源软件、AI模型、AI变现 - 小众AI DevDocs 是一个完全免费的开源工具,由 CyberAGI 团队开发,托管在 GitHub 上。它专为程序员和软件开发…...
