算法魅力揭秘:螺旋矩阵 II 的模拟填充与规则总结
算法魅力揭秘:螺旋矩阵 II 的模拟填充与规则总结
作为一个算法人,我们经常在竞赛和面试中遇到各种“矩阵类”问题,而螺旋矩阵 II 是其中一颗耀眼的明星。今天我将带大家从直观理解到实战代码,全面拆解螺旋矩阵 II 的规律与实现。相信读完这篇文章,你不仅能掌握这个题目,更能学到如何将“模拟法”巧妙运用于复杂场景。
一、问题描述与案例分析
问题:给定一个正整数 n,要求生成一个 n x n 的矩阵,其数字按照螺旋顺序从 1 填充到 n*n。
比如,当 n = 3 时,结果矩阵应为:
1 2 3
8 9 4
7 6 5
螺旋矩阵的独特之处在于:我们需要动态调整填充方向(右 → 下 → 左 → 上),并处理边界条件,防止越界或重复填充。这是一次对模拟能力与逻辑细致性的全面考验。
二、解题思路:规则分解与模拟填充
1. 明确填充方向
螺旋矩阵的填充遵循固定顺序:
- 右:列坐标 +1,行坐标不变;
- 下:行坐标 +1,列坐标不变;
- 左:列坐标 -1,行坐标不变;
- 上:行坐标 -1,列坐标不变。
通过定义一个方向数组:
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)] # 右、下、左、上
每次转向时调整当前方向索引,便能轻松完成方向切换。
2. 边界条件与填充控制
为了防止越界或重复填充,我们需设置动态边界,或者通过矩阵值 0 判断当前格子是否已填充。
3. 填充过程模拟
从左上角((0, 0))开始填充,每次根据当前方向计算下一个位置,若越界或碰壁则转向,直到填满所有格子。
三、代码实现:详细拆解与示例
以下是 Python 实现螺旋矩阵的完整代码,并附有详细注释说明每一步的逻辑。
def generate_spiral_matrix(n):"""生成一个 n x n 的螺旋矩阵"""# 初始化一个空矩阵matrix = [[0] * n for _ in range(n)]# 定义填充方向:右、下、左、上directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]direction_index = 0 # 当前方向索引,从右开始# 起始位置row, col = 0, 0for num in range(1, n * n + 1): # 填充数字从1到n*nmatrix[row][col] = num # 填入当前数字# 计算下一个位置next_row = row + directions[direction_index][0]next_col = col + directions[direction_index][1]# 如果越界或下一个格子已填充,则切换方向if not (0 <= next_row < n and 0 <= next_col < n) or matrix[next_row][next_col] != 0:direction_index = (direction_index + 1) % 4 # 顺时针切换方向next_row = row + directions[direction_index][0]next_col = col + directions[direction_index][1]# 更新当前位置row, col = next_row, next_colreturn matrix
示例运行
以 n=4 为例,调用函数并打印结果:
result = generate_spiral_matrix(4)
for row in result:print(row)
输出结果:
[1, 2, 3, 4]
[12, 13, 14, 5]
[11, 16, 15, 6]
[10, 9, 8, 7]
四、代码逻辑总结
- 初始化矩阵与方向数组:构造空矩阵,并定义方向数组管理填充路径。
- 填充循环:从数字
1到n*n,逐格填入。 - 方向判断与切换:每次尝试移动到下一个位置,若越界或碰壁,则调整方向。
- 动态更新坐标:确保当前位置随方向变化而改变。
这种方法逻辑清晰,代码简洁,易于扩展到更复杂的规则中,比如支持不同形状的“螺旋”。
五、常见问题与优化思路
-
问题:重复填充或越界
- 原因:边界条件判断不全。
- 解决方案:严格检查下一步是否超出范围或已被填充。
-
问题:代码复杂度高
- 原因:方向切换逻辑不清晰。
- 解决方案:使用方向数组统一管理,避免硬编码。
-
优化建议
- 若矩阵尺寸极大,可以提前计算需要填充的范围,减少不必要的循环检查。
六、螺旋矩阵的延伸应用
螺旋矩阵的填充策略不仅适用于二维数组问题,还能在以下场景中应用:
- 数据可视化:生成图像处理中的“螺旋”扫描路径。
- 游戏开发:实现迷宫类游戏的路径探索。
- 硬件设计:优化存储器访问路径以减少延迟。
七、结语
螺旋矩阵 II 虽然是一个看似基础的题目,但它在数据模拟与逻辑推理上的要求却不低。从方向管理到边界判断,每一步都考验着代码实现的严谨性。更重要的是,通过这个题目,我们能学到模拟类算法的核心思想,为解决更多复杂问题打下基础。
相关文章:

算法魅力揭秘:螺旋矩阵 II 的模拟填充与规则总结
算法魅力揭秘:螺旋矩阵 II 的模拟填充与规则总结 作为一个算法人,我们经常在竞赛和面试中遇到各种“矩阵类”问题,而螺旋矩阵 II 是其中一颗耀眼的明星。今天我将带大家从直观理解到实战代码,全面拆解螺旋矩阵 II 的规律与实现。…...

一个插件,免费使用所有顶级大模型(Deepseek,Gpt,Grok,Gemini)
DeepSider是一款集成于浏览器侧边栏的AI对话工具,可免费使用所有顶级大模型 包括GPT-4o,Grok3,Claude 3.5 Sonnet,Claude 3.7,Gemini 2.0,Deepseek R1满血版等 以极简交互与超快的响应速度,完成AI搜索、实时问答、内容创作、翻译、…...

springboot Filter实现请求响应全链路拦截!完整日志监控方案
一、为什么你需要这个过滤器? 日志痛点: 🚨 请求参数散落在各处? 🚨 响应数据无法统一记录? 🚨 日志与业务代码严重耦合? 解决方案: 一个Filter同时拦截请…...
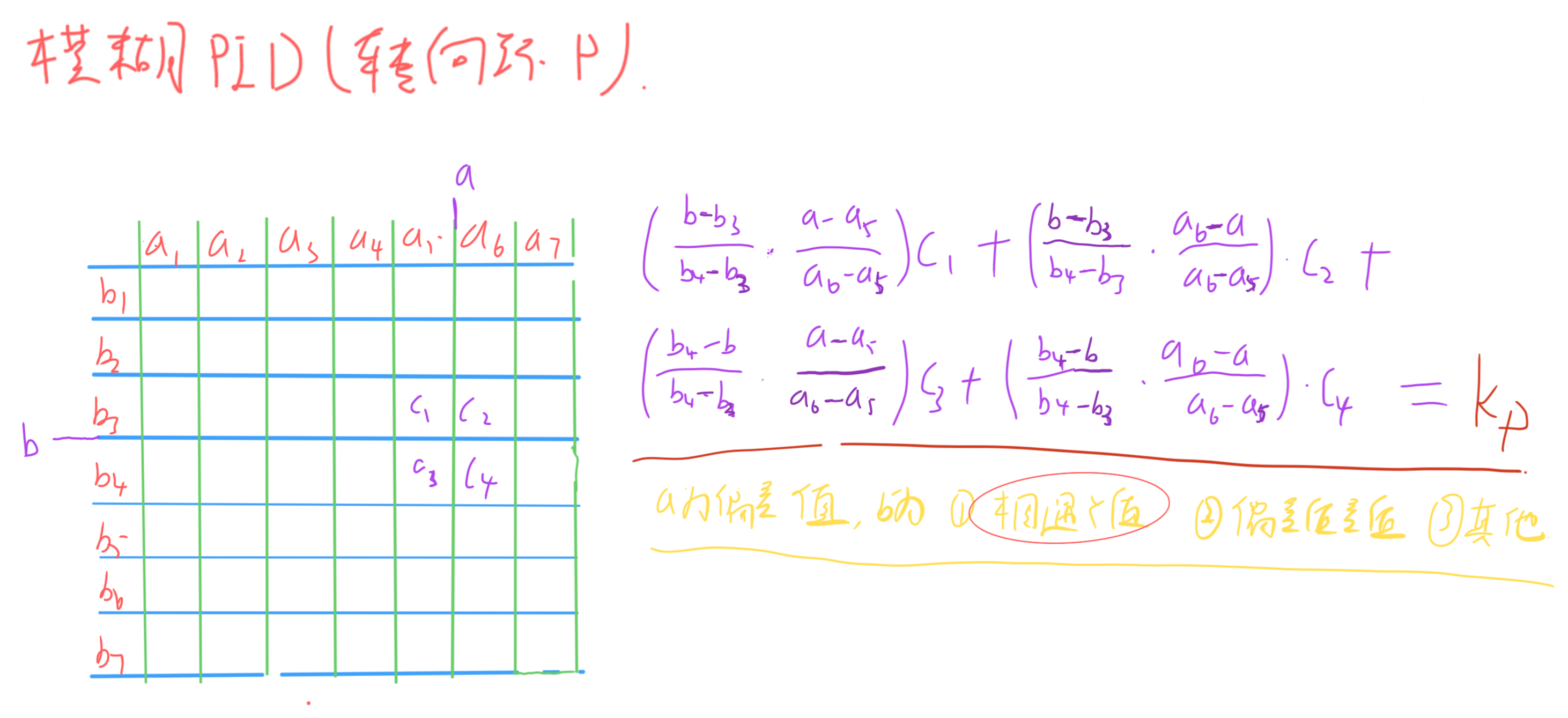
智能车摄像头开源—9 动态权、模糊PID、速度决策、路径优化
目录 一、前言 二、动态权 1.概述 2.偏差值加动态权 三、模糊PID 四、速度决策 1.曲率计算 2.速度拟合 3.速度控制 五、路径 六、国赛视频 一、前言 在前中期通过识别直道、弯道等元素可进行加减速操作实现速度的控制,可进一步缩减一圈的运行速度ÿ…...

《2025蓝桥杯C++B组:D:产值调整》
**作者的个人gitee** 作者的算法讲解主页▶️ 每日一言:“泪眼问花花不语,乱红飞过秋千去🌸🌸” 题目 二.解题策略 本题比较简单,我的思路是写三个函数分别计算黄金白银铜一次新产值,通过k次循环即可获…...

蓝队技能-Web入侵-入口查杀攻击链
Web攻击事件 分析思路: 1、利用时间节点筛选日志行为 2、利用对漏洞进行筛选日志行为 3、利用后门查杀进行筛选日志行为 4、利用文件修改时间筛选日志行为 Web日志分析 明确存储路径以及查看细节 常见中间件存储路径 IIS、Apache、Tomcat 等中间件的日志存放目…...

Android11车载WiFi热点默认名称及密码配置
一、背景 基于车厂信息安全要求,车载热点默认名称不能使用统一的名称,以及默认密码不能为简单的1~9。 基于旧项目经验,组装工厂自动化测试及客户整车组装的时候均存在多台设备同时打开,亦不太推荐使用统一的热点名称,连接无法区分。 二、需求 根据客户的要求,默认名称…...

对于GAI虚假信息对舆论观察分析
摘要 生成式人工智能(Generative Artificial Intelligence, GAI)的技术革新重构了信息生产机制,但也加剧了虚假信息对舆论生态的异化风险。 关键词:生成式人工智能、虚假信息、舆论异化、智能治理 一、生成式人工智能虚假信息下…...

问题 | 对于初学者来说,esp32和stm32哪个比较适合?
对于初学者选择ESP32还是STM32入门嵌入式开发,需综合考虑学习目标、兴趣方向及未来职业规划。以下是两者的对比分析及建议: 1. 适合初学者的关键因素 ESP32的优势 内置无线通信:集成Wi-Fi和蓝牙功能,无需额外模块即可开发物联网…...

grafana/loki 部署搜集 k8s 集群日志
grafana/loki 和 grafana/loki-stack 的区别 Grafana 提供了多个 Helm Chart 用于在 Kubernetes 集群中部署 Loki 及相关组件,其中主要包括 grafana/loki 和 grafana/loki-stack。它们的主要区别如下: 1.grafana/loki Helm Chart: 专注于 Loki 部署: 该 Chart 专门…...

EN控制同步整流WD1020 ,3.0V-21V 的宽 VIN 输入范围,0.9V-20V 的宽输出电压范围
WD1020 是一款功能强大且性能卓越的电源管理芯片,凭借其独特的特点在众多电子设备领域中展现出广泛的应用前景。以下是对其特点和应用电路的详细阐述: 集成式功率 MOSFET:WD1020 集成了低 RDS(开)功率 MOSFETÿ…...

asm汇编语言源代码之-获取环境变量
提供1个子程序: 1. 读取环境变量 GETENVSTR 具体功能及参数描述如下 GETENVSTR PROC FAR ;IN: DSPSP SEG. ; ES:BX -> ENV VAR NAME ;OUT: DS:DX -> ENV VAR VALUE; IF DX0FFFFH, NOT FOUND ; more source code at http://www.ahjoe.com/source/srcdown.aspPU…...

2025认证杯一阶段各题需要使用的模型或算法(冲刺阶段)
A题(小行星轨迹预测) 问题一:三角测量法、最小二乘法、空间几何算法、最优化方法 问题二:Gauss/Laplace轨道确定方法、差分校正法、数值积分算法(如Runge-Kutta法)、卡尔曼滤波器 B题(谣言在…...

①(PROFINET 转 EtherNet/IP)EtherCAT/Ethernet/IP/Profinet/ModbusTCP协议互转工业串口网关
型号 协议转换通信网关 PROFINET 转 EtherNet/IP MS-GW32 概述 MS-GW32 是 PROFINET 和 EtherNet/IP 协议转换网关,为用户提供两种不同通讯协议的 PLC 进行数据交互的解决方案,可以轻松容易将 EtherNet/IP 网络接入 PROFINET 网络中,方便…...

LeetCode 3272.统计好整数的数目:枚举+排列组合+哈希表
【LetMeFly】3272.统计好整数的数目:枚举排列组合哈希表 力扣题目链接:https://leetcode.cn/problems/find-the-count-of-good-integers/ 给你两个 正 整数 n 和 k 。 如果一个整数 x 满足以下条件,那么它被称为 k 回文 整数 。 x 是一个…...

Linux中的tar -P选项
tar -P选项 Linux中的tar命令可用于文件和目录的归档以及压缩解压缩。而其中的-P选项是什么含义呢?下面我们就来看一看 1、不添加-P选项 对于如下压缩命令: tar -czvf pkg.tar.gz /opt/software执行该命名,控制台首行输出将会提示…...

Linux目录探秘:文件系统的核心架构
引言 Linux文件系统就像一棵精心设计的大树🌳,每个分支都有其特定的用途和规范。与Windows不同,Linux采用单一的目录结构,所有设备、分区和网络资源都挂载在这个统一的目录树下。本文将带你深入探索Linux目录结构的奥秘ÿ…...

国标GB28181视频平台EasyCVR如何搭建汽车修理厂远程视频网络监控方案
一、背景分析 近年我国汽车保有量持续攀升,与之相伴的汽车保养维修需求也逐渐提高。随着社会经济的发展,消费者对汽车维修服务质量的要求越来越高,这使得汽车维修店的安全防范与人员管理问题面临着巨大挑战。 多数汽车维修店分布分散&#…...

python【标准库】multiprocessing
文章目录 介绍多进程Process 创建子进程共享内存数据多进程通信Pool创建子进程多进程案例多进程注意事项介绍 python3.10.17版本multiprocessing 是一个多进程标准模块,使用类似于threading模块的API创建子进程,充分利用多核CPU来并行处理任务。提供本地、远程的并发,高效避…...

南墙WAF非标端口防护实战解析——指定端口安全策略深度剖析
本文系统解析非标端口DDoS攻击防护难点,重点阐述南墙WAF在指定端口防御中的技术突破。通过某金融机构真实攻防案例,结合Gartner最新防御架构模型,揭示如何构建基于智能流量建模的精准防护体系,为金融、政务等关键领域提供可落地的…...
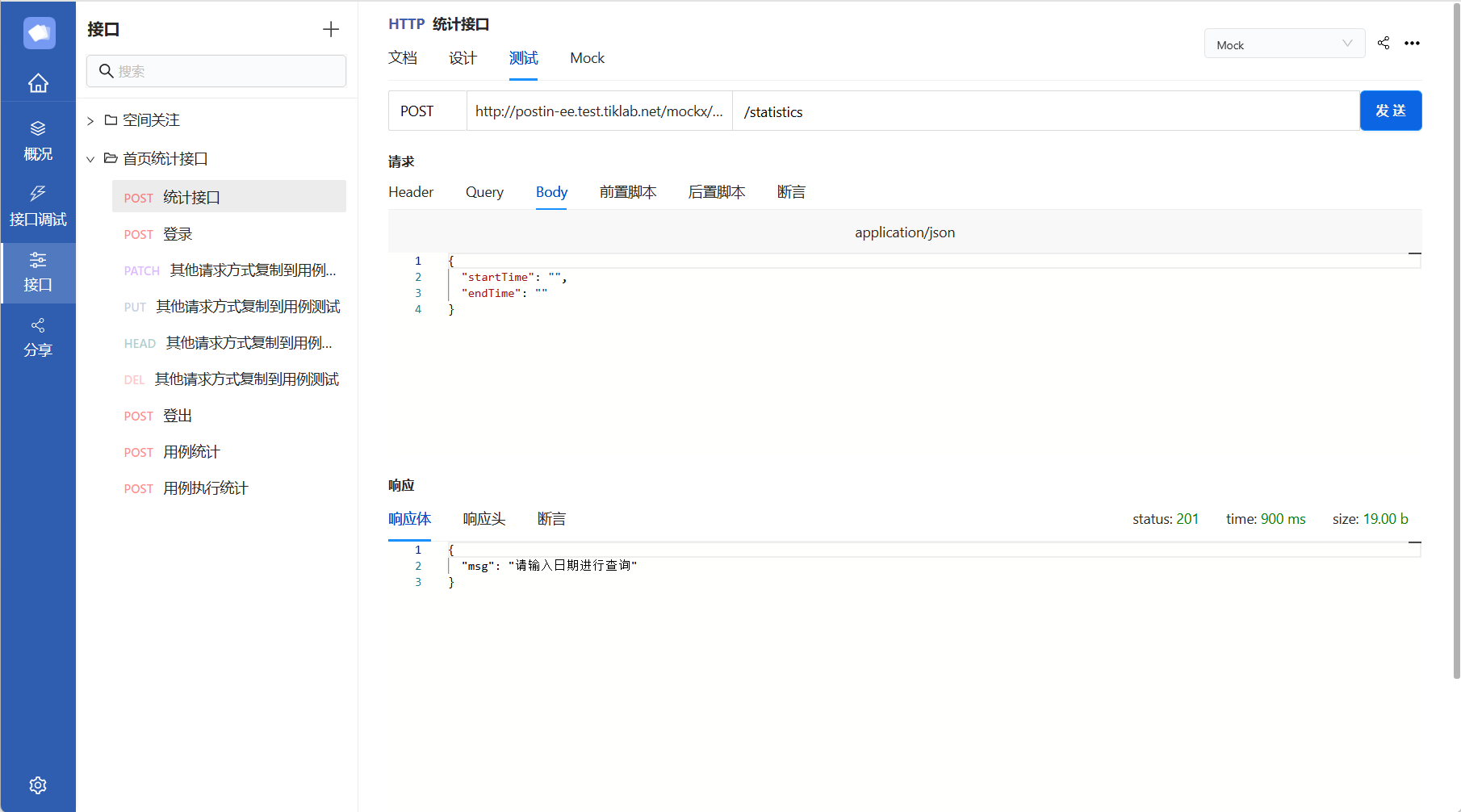
PostIn安装及入门教程
PostIn是一款国产开源免费的接口管理工具,包含项目管理、接口调试、接口文档设计、接口数据MOCK等模块,支持常见的HTTP协议、websocket协议等,支持免登陆本地接口调试,本文将介绍如何快速安装配置及入门使用教程。 1、安装 私有…...

spring cloud微服务API网关详解及各种解决方案详解
微服务API网关详解 1. 核心概念 定义:API网关作为微服务的统一入口,负责请求路由、认证、限流、监控等功能,简化客户端与后端服务的交互。核心功能: 路由与转发:将请求分发到对应服务。协议转换:HTTP/HTTP…...

最新版PhpStorm超详细图文安装教程,带补丁包(2025最新版保姆级教程)
目录 前言 一、PhpStorm最新版下载 二、PhpStorm安装 三、PhpStorm补丁 四、运行PhpStorm 前言 PhpStorm 是 JetBrains 公司推出的 专业 PHP 集成开发环境(IDE),专为提升 PHP 开发效率设计。其核心功能包括智能代码补全、实时语法错误检…...

FileInputStream 详解与记忆方法
FileInputStream 详解与记忆方法 一、FileInputStream 核心概念 FileInputStream 是 Java 中用于从文件读取原始字节的类,继承自 InputStream 抽象类。 1. 核心特点 特性说明继承关系InputStream → FileInputStream数据单位字节(8bit)用…...

【计算机网络】同步操作 vs 异步操作:核心区别与实战场景解析
📌 引言 在网络通信和分布式系统中,**同步(Synchronous)和异步(Asynchronous)**是两种基础却易混淆的操作模式。本文将通过代码示例、生活类比和对比表格,帮你彻底理解它们的区别与应用场景。 1…...

linux kernel arch 目录介绍
一:arch 目录 二:常用arch...

ES6变量声明:let、var、const全面解析
一、引言 ECMAScript 6(简称 ES6)的发布为 JavaScript 带来了许多革命性的变化,其中变量声明方式的更新尤为重要。let、var和const成为开发者日常编码中频繁使用的关键字。 本文将深入解析这三种声明方式的核心特性、区别及最佳实践ÿ…...

Linux 入门八:Linux 多进程
一、概述 1.1 什么是进程? 在 Linux 系统中,进程是程序的一次动态执行过程。程序是静态的可执行文件,而进程是程序运行时的实例,系统会为其分配内存、CPU 时间片等资源。例如,输入 ls 命令时,系统创建进程…...

单调栈 —— 1.基本概念与核心算法
1. 基本概念 1.1 知识预备 在理解单调栈之前,我们需要先掌握两个基础概念:栈(Stack) 和 单调性(Monotonicity)。 什么是栈(Stack) 栈是一种**后进先出(LIFO, Last-In…...

工程师 - 场效应管分类
What Are the Different Types of FETs? Pulse Octopart Staff Jul 31, 2021 Field effect transistors (FETs) are today’s workhorses for digital logic, but they enjoy plenty of applications outside of digital integrated circuits, everything from motor driver…...
