【数据结构】堆排序详细图解
堆排序目录
- 1、什么是堆?
- 1.1、什么是大顶堆
- 1.2、什么是小顶堆
- 2、堆排序的过程
- 3、堆排序的图解
- 3.1、将数组映射成一个完全二叉树
- 3.2、将数组转变为一个大顶堆
- 3.3、开始进行堆排序
- 4、堆排序代码
1、什么是堆?
堆的定义:在一棵完全二叉树中,每一棵子树的根节点值均大于或小于其左右子树的所有根节点值,被称为堆。其中每一棵子树的根节点值均大于左右子树的节点时,这棵树被称为大顶堆,反之,被称为小顶堆。
堆的特殊定义导致了堆具有特殊的结构,也就是说,一个堆的根节点,肯定是最大/最小的,因此,堆排序就是要将一串数组放进一个堆中去,先将这个堆构建好,然后我们就可以肯定堆顶元素是这串数组中最大/最小的了,之后我们就取走堆顶元素,将堆中最后一个元素放到堆顶,然后再维护这个堆,让它重新成为一个合法的堆即可。
1.1、什么是大顶堆

我们对堆中的节点按层进行编号,映射到数组中就是下面这个样子:

大顶堆特点: a r r [ i ] > = a r r [ 2 i + 1 ] & & a r r [ i ] > = a r r [ 2 i + 2 ] arr[i]>=arr[2i+1]\&\&arr[i]>=arr[2i+2] arr[i]>=arr[2i+1]&&arr[i]>=arr[2i+2]
1.2、什么是小顶堆


小顶堆特点: a r r [ i ] < = a r r [ 2 i + 1 ] & & a r r [ i ] < = a r r [ 2 i + 2 ] arr[i]<=arr[2i+1]\&\&arr[i]<=arr[2i+2] arr[i]<=arr[2i+1]&&arr[i]<=arr[2i+2] //i对应第几个节点,i从0开始标号
一般升序采用大顶堆,降序采用小顶堆
2、堆排序的过程
堆排序的过程:
-
根据拿到的数组构建大顶堆/小顶堆;
-
从堆顶取走元素,放到其应该存在的位置中去。从堆底拿到堆中最后一个元素,放到堆顶,此时这个堆很可能不再合法也就是说不再是一个堆;
-
维护这个堆,通过自己写的方法调整堆中节点结构,让它重新变成一个堆;
-
重复2,3过程,直到堆被取空,此时数组也被完全排列好;
3、堆排序的图解
3.1、将数组映射成一个完全二叉树
我们先自己写了一个无序的数组,如图所示,这个数组是很没有规律的。然后我们既然想把这个数组构建成堆

接下来,我们根据这个数组的结构映射出一个完全二叉树的结构,如下图所示:

3.2、将数组转变为一个大顶堆
在这里我们使用大顶堆进行排序,基于小顶堆的堆排序和这里的算法思路相同,只是实现起来有微小的差异,不过需要声明的是:基于数组的堆排序使用大顶堆排序更加方便,写起来代码量更少一些。
大顶堆的构建,我们可以使用递归的方法来构建,但是这里我们暂且不深入研究递归,因此我们使用从堆底元素一个个排查构建的基础手段进行堆的构建,也就是从数组尾部一个一个往前找,直到找到第一个不是叶子结点的节点后,我们对以它为根节点的子树进行整改,让其成为一个堆,这样一个个的往前遍历整改,就能够使得这棵树完全成为一个堆。这里只是简述了我的堆构建算法的大体思路,其中有很多细节将在下面进行详细的展示,同时使用我的算法在构建堆的时候存在一个非常重要的细节,它关系到这个堆能否被成功构建,接下来我们开始详细讲解如何构建一个堆。
-
后往前找,找到了第一个不是叶子结点的节点,如图所示:

可见该节点的叶子节点都小于根节点,也就是15,因此这棵子树本身就是一个大顶堆,我们继续向前遍历。 -
这时我们遍历到了值为7的节点,这个节点也大于其左子树和右子树,因此它也是一个大顶堆,我们继续向前遍历:

-
我们这时遍历到了值为1的节点,很不幸,它小于它的左子树和右子树,它不再是堆了:

这时我们应该怎么做?我们应该从它的
左右孩子中挑选出最大的一个,然后和根节点进行交换,这样就足以保证这棵子树的根节点大于它的所有直接孩子了。这里我们进行交换,会得到一个这样的新结构:
-
我们这时遍历到了以值为3的节点为根的子树,这个子树显然也不是一个大顶堆,3比它的左右孩子都小,如图所示:

这时我们需要将其变成一个大顶堆,有了前面的经验,我们做起来轻车熟路,选择根节点孩子节点中的最大值和根节点交换就行了,如图所示:
等等!这,这不对吧?这棵子树的根节点确确实实已经大于它的左右
直接孩子了,但是,由于3和15的交换,导致了该子树的右子树不再是一个大顶堆。现在,3是该子树的右子树的根节点,而这个根节点的右孩子是12,12大于3,它已经不符合大顶堆的概念了。这时,重要的知识点来了:由于大顶堆构建导致的一次节点值互换,有极大的可能直接导致以参与值交换的孩子节点为根节点的子树不再是一个大顶堆,简而言之,大顶堆的构建过程中的值互换操作,会导致一个更小的子树不再是大顶堆,放到这里就是,节点值为3的子树,为了变成大顶堆,和它的右孩子节点,也就是值为15的节点发生了交换,这时这颗子树的根节点值不再是3了,而是15,如上图所示,而这时,这个子树的右子树的根节点不再是15了,而变成了3,这就直接导致这个右子树不再是堆了,其有序性遭到了破坏。这时,我们要继续深入,攘外必先安内,解决掉这个问题。我们将当前的游标指向当前树的右子树根节点,也就是现在值为3的节点:

我们将此刻标红的节点继续处理,变成大顶堆,它没有右孩子,只有左孩子,因此不需要找最大孩子,直接交换就行:
现在我们将解决了刚才的问题,现在以15为根节点(也就是最初以3为根节点)的那个子树,彻彻底底确确实实的变成大顶堆了。可见,关于堆的维护,其实是穿插在堆的构建中的,构建堆的操作可能导致一个子树不再是堆,这时我们就应该在一次交换操作之后检索以参与交换的孩子节点为根节点的子树是否还是一个堆,如果不是了,那么我们必须要将当前的根节点游标指向它,将以它为根节点的子树作为新的问题规模,重复堆构建操作。现在我们解决了这个问题,就要回退到之前的位置,并继续向前遍历。 -
现在我们终于遍历到首节点了,也就是堆顶,或者说这棵树的根节点,也就是值为6的节点:

我们通过观察发现,现在这棵树显然不是一个大顶堆,根节点的左右孩子都比根节点大,我们挑选最大的
直接孩子也就是15,和6交换:

有了之前的经历,我们已经见怪不怪了,由于6和15的交换,导致了这棵树的左子树不再是一个堆,因为现在以6为根节点的子树小于它的直接左右孩子的值,也就是6和12,好事多磨,我们没有办法,只得向下深入,将游标重新指向当前值为6的节点,将其重新进行堆构建:

我们发现当前子树的根节点的左右孩子最大的是12,因此我们做一个交换,并且在交换后我们将游标指向参与交换的孩子节点位置,检测这次交换是否造成了子树堆的破坏:

好在没有,现在我们将游标回退到之前的位置,一个大顶堆也宣告完成:
以上就是堆构建的过程,然而,你以为这就完了吗?答案是还没有,这只是把一个堆构建了出来,我们实际上还没有开始进行排序,但是实际上整个过程我们已经完成了大半了,堆的构建以及维护就是上面讲的内容了,而这些内容就是最为核心的内容,并且这个构建算法需要在堆排序中反复使用,因此大家要多加学习。接下来,我们开始进行堆排序。
3.3、开始进行堆排序
那么,堆排序的过程是怎样的呢?现在我们已经得到了构建一个大顶堆的算法,因此我们现在可以对这个堆进行一些操作并有自信将其变回一个新的大顶堆了。所以我们先将堆顶元素和堆底元素进行替换:

也就是将15和3进行互换,如上图所示。在互换后我们会得到如下图所示的一个新树,此时它已经不是大顶堆了:

之后,我们将堆底元素拿走,放到数组的最末端去,有:

在这个操作之后,我们发现以该树根节点为根节点的子树不再是大顶堆了,因为根节点发生了变化,因此我们对这棵树进行维护,使用上文“将数组转变为一个大顶堆”中提到的方法,让这棵新树重现变为大顶堆:
先让3和12交换:

然后我们发现有一棵左子树不再是大顶堆了,我们继续交换:

在此之后,又发现更小的一棵子树不是大顶堆了,我们继续进行堆维护操作:

至此,一棵新的大顶堆树又完成了,我们重复上文提到的堆顶元素和堆底元素交换的过程,并同样重复拿走交换后的堆底元素的操作:



至此,我们又拿到了除15外最大的数字并排列到了15之后,重复这个过程,我们最终将得到一个从小到大的有序数组。在每次交换取数之后,再次进行堆的维护,这样一来我们就可以不断的取走当前剩余数字中最大的,并维持大顶堆,保证我们下一次取数也能立刻找到最大的。以上就是堆排序的过程。
4、堆排序代码
public class HeapSort {public static void main(String[] args) {int[] arr = new int[] { 5, 2, 1, 6, 4, 8, 11, 34, 56, 17, 26 };// 测试数组heapSort(arr);System.out.println(Arrays.toString(arr));}public static void heapSort(int[] arr) {for (int i = arr.length - 1; i >= 0; i--) {adjustSort(arr, i, arr.length);}for (int i = arr.length - 1; i >= 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;adjustSort(arr, 0, i);}}public static void adjustSort(int[] arr, int parent, int lenght) {int temp = arr[parent];int Child = 2 * parent + 1;while (Child < lenght) {// 找到左右子节点中较大的那个节点,如果左边大就用child,如果右边大就用child++if (Child + 1 < lenght && arr[Child] < arr[Child + 1]) {Child++;}if (temp >= arr[Child]) {break;}arr[parent] = arr[Child];parent = Child;// 查找当前节点的子节点,如果有子节点,继续调整Child = parent * 2 + 1;}// 交换数据arr[parent] = temp;}
}
adjustSort负责维护大顶堆,heapSort负责将堆顶元素与最后一个数对调,然后重复前面的数
码字不易,如果有收获不妨点赞、收藏、关注支持一下,各位的支持就是我创作的最大动力❤️

相关文章:

【数据结构】堆排序详细图解
堆排序目录 1、什么是堆?1.1、什么是大顶堆1.2、什么是小顶堆 2、堆排序的过程3、堆排序的图解3.1、将数组映射成一个完全二叉树3.2、将数组转变为一个大顶堆3.3、开始进行堆排序 4、堆排序代码 1、什么是堆? 堆的定义:在一棵完全二叉树中&a…...
如何排查Dubbo的序列化问题?)
Dubbo(45)如何排查Dubbo的序列化问题?
排查Dubbo的序列化问题需要从多个角度进行分析,包括序列化协议的配置、序列化对象的定义、序列化框架的兼容性等。以下是详细的排查步骤及相关代码示例: 1. 检查序列化协议配置 Dubbo支持多种序列化协议(如Hessian、Kryo、FST等)…...

有哪些基于solidity的应用
🔥 Solidity 常见应用分类(附例子) 🏦 1. DeFi(去中心化金融) Solidity 的最大应用场景之一。 项目功能示例合约逻辑Uniswap去中心化交易所(AMM)流动性池、定价算法、swap函数Aave /…...

CST1016.基于Spring Boot+Vue高校竞赛管理系统
计算机/JAVA毕业设计 【CST1016.基于Spring BootVue高校竞赛管理系统】 【项目介绍】 高校竞赛管理系统,基于 DeepSeek Spring AI Spring Boot Vue 实现,功能丰富、界面精美 【业务模块】 系统共有两类用户,分别是学生用户和管理员用户&a…...

安卓性能调优之-掉帧测试
掉帧指的是某一帧没有在规定时间内完成渲染,导致 UI 画面不流畅,产生视觉上的卡顿、跳帧现象。 Android目标帧率: 一般情况下,Android设备的屏幕刷新率是60Hz,即每秒需要渲染60帧(Frame Per Second, FPS&a…...

GPT-SoVITS:5 步实现 AI 语音克隆
在 AI 技术高速迭代的今天,语音合成早已突破”机械朗读“的局限 —— 从短视频创作者的虚拟配音、游戏角色的个性化声线,到智能客服的自然交互,GPT-SoVITS正凭借其强大的多模态融合能力,成为实现”AI 声音克隆“与“情感化语音生成…...

记录:安装 Docker Desktop 时直接设置安装路径及容器存储路径
近期学用 deepseek 本地知识库的构建,准备尝试几个不同的 RAG 工具,结果基本都需要 Docker 支持,故又重新拾起 Docker 来安装,刚好看到个不用目录链接就可以直接设置安装路径的方法,就记录一下,以免以后忘…...

AI IDE 提示词
好的,这就将之前的分析内容整理成一篇适合发布在 CSDN 上的博客文章。 告别代码生成混乱:AI IDE 提示词模式权威指南 作者: (你的名字/昵称) 日期: 2025年4月14日 前言 随着人工智能技术的飞速发展,AI 助手(如 GitHub Copilot…...

Vue使用axios实现:上传文件、下载文件
Vue 使用 axios 框架,系列文章: 《Vue使用axios实现Ajax请求》 《Vue使用axios二次封装、解决跨域问题》 《Vue使用axios实现:上传文件、下载文件》 在实际开发过程中,浏览器通常需要和服务器端进行数据交互。而 Vue.js 并未提供与服务器端通信的接口。Axios 提供了一些方便…...

QPS是什么??
QPS QPS 是 Queries Per Second 的缩写,指每秒处理的查询请求数量,是衡量系统性能和吞吐量的重要指标,尤其在以下场景中广泛应用: 1. 数据库系统 QPS表示数据库每秒能够处理的查询次数,反映数据库的查询处理能力。 …...

算法训练之贪心
♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥ ♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥ ♥♥♥我们一起努力成为更好的自己~♥♥♥ ♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥ ♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥ ✨✨✨✨✨✨ 个…...

Vagrant 安装指南:从零开始搭建开发环境
Vagrant 是一款强大的虚拟化工具,能够帮助开发者快速创建和管理轻量级的、可复制的开发环境。它通过与 VirtualBox、VMware 或 Hyper-V 等虚拟机提供程序结合使用,让你在本地轻松运行虚拟机。本文将详细介绍如何在 Windows、macOS 和 Linux 系统上安装 V…...

APIGen-MT:高效生成多轮人机交互Agent数据的两阶段框架
APIGen-MT:高效生成多轮人机交互数据的两阶段框架 引言 随着人工智能技术的飞速发展,AI代理(Agent)已从简单的聊天机器人发展为能够执行复杂现实任务的系统,例如管理金融交易、安排预约和处理客户服务等。然而&#x…...

【NLP】 21. Transformer整体流程概述 Encoder 与 Decoder架构对比
1. Transformer 整体流程概述 Transformer 模型的整个处理流程可以概括为从自注意力(Self-Attention)到多头注意力,再加上残差连接、层归一化、堆叠多层的结构。其核心思想是利用注意力机制对输入进行并行计算,从而避免传统 RNN …...

《Vue Router实战教程》21.扩展 RouterLink
欢迎观看《Vue Router 实战(第4版)》视频课程 扩展 RouterLink RouterLink 组件提供了足够的 props 来满足大多数基本应用程序的需求,但它并未尝试涵盖所有可能的用例,在某些高级情况下,你可能会发现自己使用了 v-sl…...

开发一个答题pk小程序的大致成本是多少
答题 PK 小程序通常指的是一种允许用户之间进行实时或异步答题竞赛的应用程序,可能结合PK答题、积分系统、排行榜等功能。 一、首先,确定答题 PK 小程序的基本功能模块。这可能包括用户注册登录、题库管理、题目类型(单选、多选、判断等&am…...

Android 应用蓝牙连接通信实现
Android 应用蓝牙连接通信实现,主要包括如下步骤: 一.打开蓝牙 // 获取蓝牙适配器 BluetoothAdapter bluetoothAdapter BluetoothAdapter.getDefaultAdapter() 1.判断蓝牙是否打开, bluetoothAdapter.isEnabled() 2. 如果未打开,执行打开蓝牙…...

GPT-2 语言模型 - 模型训练
本节代码是一个完整的机器学习工作流程,用于训练一个基于GPT-2的语言模型。下面是对这段代码的详细解释: 文件目录如下 1. 初始化和数据准备 设置随机种子 random.seed(1002) 确保结果的可重复性。 定义参数 test_rate 0.2 context_length 128 tes…...

科技项目验收测试包括哪些内容?有什么作用?
在现代科技快速发展的背景下,科技项目的验收测试已成为项目管理中的重要环节。科技项目验收测试是一种系统性的方法,旨在评估一个科技项目是否达到预定的技术指标和要求,确认项目的完成质量。该测试通常在项目实施完成后进行,通过…...

Java 设计模式:组合模式详解
Java 设计模式:组合模式详解 组合模式(Composite Pattern)是一种结构型设计模式,它允许将对象组织成树形结构,以统一的方式处理单个对象和对象集合。组合模式适用于需要表示“部分-整体”层次结构的场景,例…...

java实现加密解密
AES加密/解密核心步骤 参考 https://flying-fish.blog.csdn.net/article/details/142688630?fromshareblogdetail&sharetypeblogdetail&sharerId142688630&sharereferPC&sharesourceweixin_48616345&sharefromfrom_link工具类 import javax.crypto.Cip…...

websoket 学习笔记
目录 基本概念 工作原理 优势 应用场景 HTTP协议与 webSoket协议之间的对比 消息推送场景 1. 轮询(Polling) 2. 长轮询(Long Polling) 3. 服务器发送事件(Server-Sent Events, SSE) 4. WebSocket…...
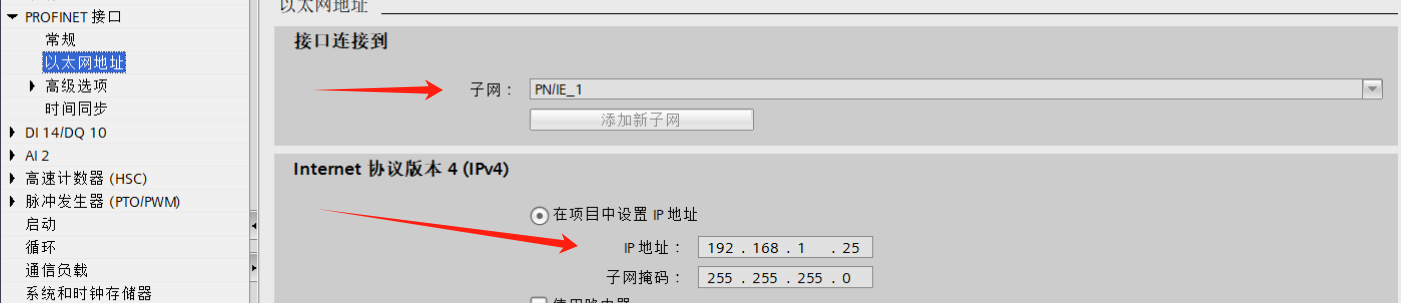
博途 TIA Portal之1200做从站与汇川EASY的TCP通讯
上篇我们写到了博途做主站与汇川EASY的通讯。通讯操作起来很简单,当然所谓的简单,也是相对的,如果操作成功一次,那么后面就很容易了, 如果操作不成功,就会很遭心。本篇我们将1200做从站,与汇川EASY做主站进行TCP的通讯。 1、硬件准备 1200PLC一台,带调试助手的PC机一…...

【数据结构_6下篇】有关链表的oj题
思路: 1.分别求出这两个链表的长度 2.创建两个引用,指向两个链表的头节点;找到长度长的链表,让她的引用先走差值步数 3.让这两个引用,同时往后走,每个循环各自走一步 然后再判定两个引用是否指向同一个…...

vscode+wsl 运行编译 c++
linux 的 windows 子系统(wsl)是 windows 的一项功能,可以安装 Linux 的发行版,例如(Ubuntu,Kali,Arch Linux)等,从而可以直接在 windows 下使用 Linux 应用程序…...
)
快速幂(蓝桥杯)
1. 递归实现 递归方法通过将问题分解为更小的子问题来实现。具体步骤如下: 如果指数 b 为 0,返回 1。 如果 b 是偶数,则递归计算 (a^2)b/2。 如果 b 是奇数,则递归计算 a⋅(a^2)(b−1)/2。 伪代码: function fas…...

狂神SQL学习笔记一:初识MySQL、关系型数据库和非关系型数据库
菜鸟教程学习一半了,但是已经疲倦了,所以换一个课程学习,来提升学习质量,可能会有很多已经学习到的地方,就当是复习巩固了。 按照SQL学习课程来划分,分为45集,所以可能也会写45篇文章ÿ…...

关于 Spring Boot 微服务解决方案的对比,并以 Spring Cloud Alibaba 为例,详细说明其核心组件的使用方式、配置及代码示例
以下是关于 Spring Boot 微服务解决方案的对比,并以 Spring Cloud Alibaba 为例,详细说明其核心组件的使用方式、配置及代码示例: 关于 Spring Cloud Alibaba 致力于提供微服务开发的一站式解决方案! https://sca.aliyun.com/?spm7145af80…...

VS 基于git工程编译版本自动添加版本号
目录 概要 实现方案 概要 最近在用visual Studio 开发MFC项目时,需要在release版本编译后的exe文件自动追加版本信息。 由于我们用的git工程管理,即需要基于最新的git 提交来打版本。 比如: MFCApplication_V1.0.2_9.exe 由于git 提交信…...

小程序开发指南
小程序开发指南 目录 1. 小程序开发概述 1.1 什么是小程序1.2 小程序的优势1.3 小程序的发展历程 2. 开发准备工作 2.1 选择开发平台2.2 开发环境搭建2.3 开发模式选择 3. 小程序开发流程 3.1 项目规划3.2 界面设计3.3 代码开发3.4 基本开发示例3.5 数据存储3.6 网络请求3.7 …...
