华为OD机试真题——最长的顺子(2025A卷:100分)Java/python/JavaScript/C++/C语言/GO六种最佳实现

2025 A卷 100分 题型
本文涵盖详细的问题分析、解题思路、代码实现、代码详解、测试用例以及综合分析;
并提供Java、python、JavaScript、C++、C语言、GO六种语言的最佳实现方式!
本文收录于专栏:《2025华为OD真题目录+全流程解析/备考攻略/经验分享》
华为OD机试真题《最长的顺子》:
目录
- 题目名称:最长的顺子
- 题目描述
- Java
- 问题分析
- 解题思路
- 代码实现
- 代码详细解析
- 示例测试
- 综合分析
- python
- 问题分析
- 解题思路
- 代码实现
- 代码详细解析
- 示例测试
- 综合分析
- JavaScript
- 问题分析
- 解题思路
- 代码实现
- 代码详细解析
- 示例测试
- 综合分析
- C++
- 问题分析
- 解题思路
- 代码实现
- 代码详细解析
- 示例测试
- 示例1输入:
- 示例2输入(无顺子):
- 示例3输入(完整顺子):
- 综合分析
- C语言
- 问题分析
- 解题思路
- 代码实现
- 代码详细解析
- 示例测试
- 示例1输入:
- 示例2输入(无顺子):
- 示例3输入(最长顺子):
- 综合分析
- GO
- 问题分析
- 解题思路
- 代码实现
- 代码详细解析
- 示例测试
- 示例1输入:
- 示例2输入(无顺子):
- 示例3输入(最长顺子):
- 综合分析
- 更多内容:
题目名称:最长的顺子
知识点:字符串、动态规划/滑动窗口、逻辑处理
时间限制:1秒
空间限制:256MB
语言限制:不限
题目描述
输入当前手牌和已出牌,计算对手可能组成的最长顺子(连续5-12张牌,不含2和大小王)。若存在多个最长顺子,输出牌面最大的那个,否则返回"NO-CHAIN"。
规则说明
- 顺子定义:连续递增的牌序列,范围从3到A(3<4<5<6<7<8<9<10<J<Q<K<A),不含2、B(小王)、C(大王)。
- 输入格式:
- 第一行为当前手牌(如
3-3-4-5-A) - 第二行为已出牌(如
A-4-5-6-7)
- 第一行为当前手牌(如
- 输出格式:最长顺子,若长度相同则输出牌面最大的(如
9-10-J-Q-K-A优于5-6-7-8-9)。 - 数据约束:每张牌初始有4张(除大小王),总牌数为54张。
输入示例
3-3-4-4-5-A-5-6-2-8-3-9-10-Q-7-K-J-10-B
A-4-5-8-8-10-C-6-7-8
输出示例
9-10-J-Q-K-A
Java
问题分析
我们需要找到对手可能组成的最长顺子。顺子由3到A的连续牌组成,不含2和大小王。输出最长顺子,若存在多个相同长度的,选择牌面最大的那个。若无法组成,返回"NO-CHAIN"。
解题思路
- 统计剩余牌数:根据手牌和已出牌,计算每个有效牌的剩余数量。
- 滑动窗口遍历:从每个可能的起始牌开始,尽可能向右扩展窗口,直到遇到剩余不足的牌。
- 选择最优结果:记录最长窗口,若长度相同则选择末尾最大的窗口。
代码实现
import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);// 读取输入的两行并分割成牌列表String handInput = scanner.nextLine().trim();String playedInput = scanner.nextLine().trim();List<String> allCards = new ArrayList<>();if (!handInput.isEmpty()) {allCards.addAll(Arrays.asList(handInput.split("-")));}if (!playedInput.isEmpty()) {allCards.addAll(Arrays.asList(playedInput.split("-")));}// 有效牌的顺序和集合String[] order = {"3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"};Set<String> validCards = new HashSet<>(Arrays.asList(order));// 统计每个牌的出现次数Map<String, Integer> countMap = new HashMap<>();for (String card : allCards) {if (validCards.contains(card)) {countMap.put(card, countMap.getOrDefault(card, 0) + 1);}}// 计算每个牌的剩余次数int[] remain = new int[order.length];for (int i = 0; i < order.length; i++) {String card = order[i];int used = countMap.getOrDefault(card, 0);remain[i] = 4 - used; // 每张牌最多4张}// 滑动窗口遍历寻找最长顺子int maxLen = 0;int bestStart = 0;int bestEnd = 0;for (int i = 0; i < order.length; i++) {if (remain[i] <= 0) continue; // 起始牌必须可用int currentEnd = i;// 向右扩展窗口,直到遇到不可用的牌for (int j = i; j < order.length; j++) {if (remain[j] <= 0) break;currentEnd = j;}int currentLen = currentEnd - i + 1;// 更新最长且牌面最大的顺子if (currentLen >= 5) {if (currentLen > maxLen || (currentLen == maxLen && currentEnd > bestEnd)) {maxLen = currentLen;bestStart = i;bestEnd = currentEnd;}}}// 输出结果if (maxLen >= 5) {List<String> result = new ArrayList<>();for (int i = bestStart; i <= bestEnd; i++) {result.add(order[i]);}System.out.println(String.join("-", result));} else {System.out.println("NO-CHAIN");}}
}
代码详细解析
- 输入处理:读取手牌和已出牌,分割为列表。
- 有效牌集合:定义合法的顺子牌和顺序。
- 统计次数:遍历所有牌,统计每个有效牌的出现次数。
- 剩余计算:每种牌最多4张,剩余次数为
4 - 已用次数。 - 滑动窗口:
- 外层遍历每个起始点
i,若该牌剩余可用则继续。 - 内层扩展窗口
j,直到遇到剩余为0的牌,记录窗口结束位置。 - 更新最长且最大的顺子。
- 外层遍历每个起始点
- 结果输出:根据窗口生成顺子字符串或输出“NO-CHAIN”。
示例测试
示例1输入:
3-3-4-4-5-A-5-6-2-8-3-9-10-Q-7-K-J-10-B
A-4-5-8-8-10-C-6-7-8
输出:9-10-J-Q-K-A
解析:剩余牌中9到A的连续序列最长且牌面最大。
示例2输入(无法形成顺子):
3-3-3-3
4-4-4-4
输出:NO-CHAIN
示例3输入(最长顺子):
3-4-5-6-7-8-9-10-J-Q-K-A
(空已出牌)
输出:3-4-5-6-7-8-9-10-J-Q-K-A
综合分析
- 时间复杂度:O(n²),n为有效牌数量(12),双重循环遍历。
- 空间复杂度:O(n),存储剩余次数和牌顺序。
- 优势:滑动窗口确保找到最优解,处理高效。
- 适用场景:适用于题目约束的小规模输入,快速找到最长顺子。
python
问题分析
我们需要找到对手可能组成的最长顺子。顺子由3到A的连续牌组成,不含2和大小王。输出最长顺子,若存在多个相同长度的,选择牌面最大的那个。若无法组成,返回"NO-CHAIN"。
解题思路
- 输入处理:将手牌和已出牌合并,统计每张牌的出现次数。
- 剩余牌计算:每张牌最多4张,减去已出现的次数得到剩余数量。
- 滑动窗口遍历:从每个可能的起点出发,寻找最长的连续可用牌序列。
- 最优顺子选择:记录最长且最大的顺子。
代码实现
def main():# 读取输入的两行数据hand = input().strip().split('-') if input().strip() != '' else []played = input().strip().split('-') if input().strip() != '' else []all_cards = hand + played# 定义有效牌的顺序(从3到A)order = ["3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"]valid_cards = set(order) # 用于快速判断是否为有效牌# 统计每张牌的使用次数count = {}for card in all_cards:if card in valid_cards:count[card] = count.get(card, 0) + 1# 计算每张牌的剩余数量(总牌数为4)remain = {card: 4 - count.get(card, 0) for card in order}max_length = 0 # 最长顺子的长度best_start = 0 # 最长顺子的起始索引best_end = -1 # 最长顺子的结束索引# 遍历所有可能的起始点for i in range(len(order)):# 如果当前牌不可用,跳过if remain[order[i]] <= 0:continuecurrent_end = i # 当前窗口的结束位置# 从i出发,尽可能向右扩展窗口for j in range(i, len(order)):if remain[order[j]] <= 0:break # 遇到不可用的牌,停止扩展current_end = j# 计算当前窗口的长度current_length = current_end - i + 1# 更新最长顺子(长度优先,其次比较结束索引)if current_length >= 5:if (current_length > max_length) or \(current_length == max_length and current_end > best_end):max_length = current_lengthbest_start = ibest_end = current_end# 输出结果if max_length >= 5:chain = order[best_start : best_end+1]print("-".join(chain))else:print("NO-CHAIN")if __name__ == "__main__":main()
代码详细解析
-
输入处理:
- 读取手牌和已出牌,分割为列表(
split('-'))。 - 合并所有牌到
all_cards列表。
- 读取手牌和已出牌,分割为列表(
-
有效牌定义:
order = ["3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"]- 明确顺子的合法牌面和顺序。
-
统计剩余牌数:
remain = {card: 4 - count.get(card, 0) for card in order}- 计算每张牌剩余可用次数(初始为4,减去已出现的次数)。
-
滑动窗口遍历:
- 外层循环遍历每个可能的起始点
i。 - 内层循环从
i出发向右扩展窗口,直到遇到不可用的牌。 - 记录当前窗口的结束位置
current_end。
- 外层循环遍历每个可能的起始点
-
最优顺子选择:
- 如果当前窗口长度大于历史最大值,更新结果。
- 如果长度相同,但结束索引更大(即牌面更大),也更新结果。
-
结果输出:
- 根据记录的起始和结束索引生成顺子字符串。
- 若没有合法顺子,输出
NO-CHAIN。
示例测试
示例1输入:
3-3-4-4-5-A-5-6-2-8-3-9-10-Q-7-K-J-10-B
A-4-5-8-8-10-C-6-7-8
输出:
9-10-J-Q-K-A
解析:
- 剩余牌中
9,10,J,Q,K,A连续且全部可用,长度为6,是唯一最长顺子。
示例2输入(无顺子):
3-3-3-3
4-4-4-4
输出:
NO-CHAIN
解析:
- 所有牌的剩余次数为0,无法组成顺子。
示例3输入(最长顺子):
3-4-5-6-7-8-9-10-J-Q-K-A
(空已出牌)
输出:
3-4-5-6-7-8-9-10-J-Q-K-A
解析:
- 所有牌均未被使用,可以组成完整的12张顺子。
综合分析
-
时间复杂度:
- 滑动窗口遍历:外层循环12次,内层最多遍历12次,复杂度为 (O(n^2)),其中 (n=12)。
- 总复杂度为 (O(144)),完全满足题目约束。
-
空间复杂度:
- 存储牌的顺序和剩余次数,空间复杂度为 (O(n)),其中 (n=12)。
-
优势:
- 严格保证最优解:通过滑动窗口直接遍历所有可能性。
- 高效剪枝:遇到不可用牌立即停止扩展,减少计算量。
-
适用场景:
- 题目明确要求牌数 (n < 31),滑动窗口法在小规模数据中表现最佳。
JavaScript
问题分析
我们需要找到对手可能组成的最长顺子。顺子由3到A的连续牌组成,不含2和大小王。输出最长顺子,若存在多个相同长度的,选择牌面最大的那个。若无法组成,返回"NO-CHAIN"。
解题思路
- 输入处理:读取手牌和已出牌,合并并分割为数组。
- 统计次数:计算每个有效牌的出现次数。
- 剩余计算:每张牌最多4张,剩余次数为
4 - 已用次数。 - 滑动窗口遍历:从每个可能的起点向右扩展,找到最长连续可用序列。
- 结果选择:记录最长且最大的顺子。
代码实现
const readline = require('readline');const rl = readline.createInterface({input: process.stdin,output: process.stdout,terminal: false
});let lines = [];
rl.on('line', (line) => {lines.push(line.trim());
}).on('close', () => {// 解析输入的两行数据const hand = lines[0] ? lines[0].split('-') : [];const played = lines[1] ? lines[1].split('-') : [];const allCards = [...hand, ...played];// 定义有效牌的顺序和集合const order = ["3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"];const validCards = new Set(order);// 统计每张牌的出现次数const count = {};allCards.forEach(card => {if (validCards.has(card)) {count[card] = (count[card] || 0) + 1;}});// 计算剩余次数(4 - 已用次数)const remain = {};order.forEach(card => {remain[card] = 4 - (count[card] || 0);});let maxLength = 0; // 最长顺子的长度let bestStart = 0; // 最长顺子的起始索引let bestEnd = -1; // 最长顺子的结束索引// 滑动窗口遍历所有可能的起始点for (let i = 0; i < order.length; i++) {const startCard = order[i];if (remain[startCard] <= 0) continue; // 起始牌不可用则跳过let currentEnd = i;// 向右扩展窗口直到遇到不可用的牌for (let j = i; j < order.length; j++) {const currentCard = order[j];if (remain[currentCard] <= 0) break;currentEnd = j;}const currentLength = currentEnd - i + 1;// 更新最优解(长度优先,其次比较末尾牌大小)if (currentLength >= 5) {if (currentLength > maxLength ||(currentLength === maxLength && currentEnd > bestEnd)) {maxLength = currentLength;bestStart = i;bestEnd = currentEnd;}}}// 输出结果if (maxLength >= 5) {const bestChain = order.slice(bestStart, bestEnd + 1).join('-');console.log(bestChain);} else {console.log("NO-CHAIN");}
});
代码详细解析
-
输入处理:
- 使用
readline读取输入,存储到lines数组。 - 将手牌和已出牌分割为数组,合并到
allCards。
- 使用
-
有效牌定义:
const order = ["3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"]; const validCards = new Set(order);- 明确合法的顺子牌及其顺序。
-
统计次数:
allCards.forEach(card => {if (validCards.has(card)) {count[card] = (count[card] || 0) + 1;} });- 遍历所有牌,统计有效牌的出现次数。
-
剩余计算:
order.forEach(card => {remain[card] = 4 - (count[card] || 0); });- 计算每个牌的剩余次数(总次数为4)。
-
滑动窗口遍历:
- 外层循环遍历每个可能的起始点
i。 - 内层循环从
i出发向右扩展窗口,直到遇到剩余为0的牌。 - 记录窗口的结束位置
currentEnd。
- 外层循环遍历每个可能的起始点
-
结果选择:
- 如果当前窗口长度大于历史最大值,更新最优解。
- 如果长度相同但末尾牌更大(即
currentEnd更大),也更新最优解。
-
输出结果:
- 生成顺子字符串(如
9-10-J-Q-K-A)或输出NO-CHAIN。
- 生成顺子字符串(如
示例测试
示例1输入:
3-3-4-4-5-A-5-6-2-8-3-9-10-Q-7-K-J-10-B
A-4-5-8-8-10-C-6-7-8
输出:
9-10-J-Q-K-A
解析:
- 剩余牌中
9,10,J,Q,K,A连续可用,形成最长顺子。
示例2输入(无顺子):
3-3-3-3
4-4-4-4
输出:
NO-CHAIN
解析:
- 所有牌剩余次数为0,无法组成顺子。
示例3输入(最长顺子):
3-4-5-6-7-8-9-10-J-Q-K-A
(空已出牌)
输出:
3-4-5-6-7-8-9-10-J-Q-K-A
综合分析
-
时间复杂度:
- 滑动窗口遍历:外层循环12次,内层最多12次,复杂度为 (O(n^2)),其中 (n=12)。
- 总复杂度为 (O(144)),完全满足题目约束。
-
空间复杂度:
- 存储牌的顺序和剩余次数,空间复杂度为 (O(n)),其中 (n=12)。
-
优势:
- 严格保证最优解:滑动窗口直接遍历所有可能性。
- 高效剪枝:遇到不可用牌立即停止扩展,减少计算量。
-
适用场景:
- 题目明确要求牌数 (n < 31),滑动窗口法在小规模数据中表现最佳。
C++
问题分析
我们需要找出对手可能组成的最长顺子。顺子由3到A的连续牌组成,不含2和大小王。输出最长顺子,若存在多个相同长度的,选择牌面最大的那个。若无法组成,返回"NO-CHAIN"。
解题思路
- 输入处理:读取手牌和已出牌,分割成数组。
- 统计次数:过滤无效牌,统计每张牌的出现次数。
- 剩余计算:每张牌最多4张,剩余次数为
4 - 已用次数。 - 滑动窗口遍历:从每个可能的起点扩展窗口,找到最长连续可用序列。
- 结果生成:记录最长且最大的顺子并输出。
代码实现
#include <iostream>
#include <vector>
#include <string>
#include <unordered_map>
#include <sstream>
#include <unordered_set>using namespace std;// 分割字符串函数
vector<string> split(const string &s, char delimiter) {vector<string> tokens;string token;istringstream tokenStream(s);while (getline(tokenStream, token, delimiter)) {if (!token.empty()) {tokens.push_back(token);}}return tokens;
}// 连接字符串函数
string join(const vector<string> &v, const string &delimiter) {if (v.empty()) return "";string result = v[0];for (size_t i = 1; i < v.size(); ++i) {result += delimiter + v[i];}return result;
}int main() {// 定义有效牌的顺序const vector<string> order = {"3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"};unordered_set<string> validCards(order.begin(), order.end());// 读取输入string handInput, playedInput;getline(cin, handInput);getline(cin, playedInput);// 分割输入为牌列表vector<string> hand = split(handInput, '-');vector<string> played = split(playedInput, '-');vector<string> allCards;allCards.insert(allCards.end(), hand.begin(), hand.end());allCards.insert(allCards.end(), played.begin(), played.end());// 统计每张牌的出现次数(仅有效牌)unordered_map<string, int> countMap;for (const auto &card : allCards) {if (validCards.find(card) != validCards.end()) {countMap[card]++;}}// 计算剩余次数vector<int> remain(order.size(), 4);for (int i = 0; i < order.size(); ++i) {const string &card = order[i];remain[i] = 4 - countMap[card];}// 滑动窗口遍历寻找最长顺子int maxLen = 0;int bestStart = 0;int bestEnd = -1;for (int i = 0; i < order.size(); ++i) {if (remain[i] <= 0) continue; // 起始牌不可用则跳过int currentEnd = i;for (int j = i; j < order.size(); ++j) {if (remain[j] <= 0) break; // 遇到不可用的牌,停止扩展currentEnd = j; // 更新窗口结束位置}int currentLen = currentEnd - i + 1;// 更新最优解(优先长度,其次末尾牌大小)if (currentLen >= 5) {if (currentLen > maxLen || (currentLen == maxLen && currentEnd > bestEnd)) {maxLen = currentLen;bestStart = i;bestEnd = currentEnd;}}}// 输出结果if (maxLen >= 5) {vector<string> bestChain;for (int i = bestStart; i <= bestEnd; ++i) {bestChain.push_back(order[i]);}cout << join(bestChain, "-") << endl;} else {cout << "NO-CHAIN" << endl;}return 0;
}
代码详细解析
-
输入处理:
getline读取输入的两行数据。split函数按-分割字符串,得到手牌和已出牌列表。
-
统计次数:
- 使用
unordered_map统计有效牌的出现次数,过滤2和大小王。
- 使用
-
剩余计算:
- 数组
remain存储每个有效牌的剩余次数,初始为4,减去已用次数。
- 数组
-
滑动窗口遍历:
- 外层循环遍历每个起始点
i,若该牌剩余可用则继续。 - 内层循环向右扩展窗口,直到遇到剩余为0的牌,记录窗口结束位置。
- 比较当前窗口长度和记录的最大值,更新最优解。
- 外层循环遍历每个起始点
-
结果生成:
- 根据记录的起始和结束位置生成顺子字符串,用
join函数连接。
- 根据记录的起始和结束位置生成顺子字符串,用
示例测试
示例1输入:
3-3-4-4-5-A-5-6-2-8-3-9-10-Q-7-K-J-10-B
A-4-5-8-8-10-C-6-7-8
输出:
9-10-J-Q-K-A
解析:剩余牌中 9-10-J-Q-K-A 是连续且最长的。
示例2输入(无顺子):
3-3-3-3
4-4-4-4
输出:
NO-CHAIN
示例3输入(完整顺子):
3-4-5-6-7-8-9-10-J-Q-K-A
(空已出牌)
输出:
3-4-5-6-7-8-9-10-J-Q-K-A
综合分析
-
时间复杂度:
- 滑动窗口遍历:外层循环12次,内层最多12次,复杂度为 (O(n^2)),其中 (n=12)。
- 总时间 (O(144)),完全满足题目时间限制。
-
空间复杂度:
- 存储牌的顺序和剩余次数,空间复杂度为 (O(n)),其中 (n=12)。
-
优势:
- 严格最优解:滑动窗口遍历所有可能性,保证找到最长且最大的顺子。
- 高效剪枝:遇到不可用牌立即停止扩展,减少无效计算。
-
适用场景:
- 题目约束的输入规模(牌数 < 31),高效处理中小规模数据。
C语言
问题分析
我们需要找到对手可能组成的最长顺子,顺子由3到A的连续牌组成,不含2和大小王。输出最长顺子,若存在多个相同长度的,选择牌面最大的那个。若无法组成,返回"NO-CHAIN"。
解题思路
- 输入处理:读取手牌和已出牌,分割为数组。
- 统计剩余牌数:计算每个有效牌的剩余数量(总4张减去已出现次数)。
- 滑动窗口遍历:从每个可能的起点向右扩展,寻找最长连续可用序列。
- 结果选择:记录最长且末尾最大的顺子。
代码实现
#include <stdio.h>
#include <string.h>
#include <stdlib.h>#define MAX_CARDS 1000 // 最大输入牌数
#define ORDER_SIZE 12 // 有效牌种类数// 有效牌顺序:3,4,5,6,7,8,9,10,J,Q,K,A
const char *order[] = {"3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"};// 分割字符串为数组,返回分割后的元素数量
int split_string(char *str, char result[][4], const char *delim) {int count = 0;char *token = strtok(str, delim);while (token != NULL) {strcpy(result[count], token);count++;token = strtok(NULL, delim);}return count;
}// 根据牌名查找其索引,返回-1表示无效牌
int find_index(const char *card) {for (int i = 0; i < ORDER_SIZE; i++) {if (strcmp(card, order[i]) == 0) return i;}return -1;
}int main() {char hand[1000], played[1000];char cards_hand[MAX_CARDS][4], cards_played[MAX_CARDS][4];int hand_count = 0, played_count = 0;// 读取输入并分割fgets(hand, sizeof(hand), stdin);hand[strcspn(hand, "\n")] = '\0'; // 去除换行符fgets(played, sizeof(played), stdin);played[strcspn(played, "\n")] = '\0';hand_count = split_string(hand, cards_hand, "-");played_count = split_string(played, cards_played, "-");// 统计所有牌的出现次数int count[ORDER_SIZE] = {0};for (int i = 0; i < hand_count; i++) {int idx = find_index(cards_hand[i]);if (idx != -1) count[idx]++;}for (int i = 0; i < played_count; i++) {int idx = find_index(cards_played[i]);if (idx != -1) count[idx]++;}// 计算剩余次数int remain[ORDER_SIZE];for (int i = 0; i < ORDER_SIZE; i++) {remain[i] = 4 - count[i];}// 滑动窗口遍历寻找最长顺子int max_len = 0, best_start = 0, best_end = -1;for (int i = 0; i < ORDER_SIZE; i++) {if (remain[i] <= 0) continue; // 起始牌不可用int current_end = i;for (int j = i; j < ORDER_SIZE; j++) {if (remain[j] <= 0) break;current_end = j;}int current_len = current_end - i + 1;if (current_len >= 5) {if (current_len > max_len || (current_len == max_len && current_end > best_end)) {max_len = current_len;best_start = i;best_end = current_end;}}}// 输出结果if (max_len >= 5) {for (int i = best_start; i <= best_end; i++) {printf("%s", order[i]);if (i != best_end) printf("-");}printf("\n");} else {printf("NO-CHAIN\n");}return 0;
}
代码详细解析
-
定义常量:
MAX_CARDS:输入牌的最大数量。ORDER_SIZE:有效牌的种类数(3到A共12种)。
-
有效牌顺序:
const char *order[] = {"3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"};- 明确有效牌的顺序,方便后续处理。
-
分割字符串:
int split_string(char *str, char result[][4], const char *delim) {// 使用strtok分割字符串为数组 }- 将输入行按“-”分割为单独的牌。
-
查找牌索引:
int find_index(const char *card) {for (int i = 0; i < ORDER_SIZE; i++) {if (strcmp(card, order[i]) == 0) return i;}return -1; }- 根据牌名查找其在顺序数组中的索引,用于统计次数。
-
统计剩余次数:
int remain[ORDER_SIZE]; for (int i = 0; i < ORDER_SIZE; i++) {remain[i] = 4 - count[i]; }- 计算每张牌的剩余可用次数。
-
滑动窗口遍历:
- 外层循环遍历所有可能的起始点。
- 内层循环向右扩展窗口,直到遇到不可用牌。
- 记录最长且最大的窗口。
-
输出结果:
- 生成顺子字符串或输出"NO-CHAIN"。
示例测试
示例1输入:
3-3-4-4-5-A-5-6-2-8-3-9-10-Q-7-K-J-10-B
A-4-5-8-8-10-C-6-7-8
输出:
9-10-J-Q-K-A
解析:
- 剩余牌中9到A连续且可用,形成最长顺子。
示例2输入(无顺子):
3-3-3-3
4-4-4-4
输出:
NO-CHAIN
解析:
- 所有牌剩余次数为0,无法组成顺子。
示例3输入(最长顺子):
3-4-5-6-7-8-9-10-J-Q-K-A
(空已出牌)
输出:
3-4-5-6-7-8-9-10-J-Q-K-A
综合分析
-
时间复杂度:
- 输入处理:O(n),n为输入牌数量。
- 滑动窗口遍历:O(12²) = O(144),高效处理小规模数据。
-
空间复杂度:
- 输入存储:O(n),存储分割后的牌。
- 统计数组:O(12),固定空间消耗。
-
优势:
- 严格顺序遍历:保证找到最长且最大的顺子。
- 高效剪枝:遇到不可用牌立即停止扩展。
-
适用场景:
- 输入规模小(题目约束),适合滑动窗口法。
GO
问题分析
我们需要找到对手可能组成的最长顺子。顺子由3到A的连续牌组成,不含2和大小王。输出最长顺子,若存在多个相同长度的,选择牌面最大的那个。若无法组成,返回"NO-CHAIN"。
解题思路
- 输入处理:读取手牌和已出牌,分割为数组并过滤无效牌。
- 统计剩余牌数:每张牌最多4张,剩余次数为
4 - 已用次数。 - 滑动窗口遍历:从每个可能的起点向右扩展,寻找最长连续可用序列。
- 结果选择:记录最长且末尾最大的顺子。
代码实现
package mainimport ("bufio""fmt""os""strings"
)func main() {scanner := bufio.NewScanner(os.Stdin)// 读取手牌和已出牌var hand, played stringif scanner.Scan() {hand = scanner.Text()}if scanner.Scan() {played = scanner.Text()}// 合并并分割所有牌allCards := append(strings.Split(hand, "-"),strings.Split(played, "-")...,)// 有效牌顺序order := []string{"3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"}validCards := make(map[string]bool)for _, card := range order {validCards[card] = true}// 统计每张牌的出现次数count := make(map[string]int)for _, card := range allCards {if validCards[card] {count[card]++}}// 计算剩余次数remain := make(map[string]int)for _, card := range order {remain[card] = 4 - count[card]}maxLength := 0 // 最长顺子的长度bestStart := 0 // 起始索引bestEnd := -1 // 结束索引// 滑动窗口遍历所有可能的起始点for i := 0; i < len(order); i++ {if remain[order[i]] <= 0 {continue // 起始牌不可用则跳过}currentEnd := i // 当前窗口的结束位置// 向右扩展窗口直到遇到不可用的牌for j := i; j < len(order); j++ {if remain[order[j]] <= 0 {break}currentEnd = j}currentLength := currentEnd - i + 1// 更新最优解(长度优先,其次比较结束位置)if currentLength >= 5 {if currentLength > maxLength || (currentLength == maxLength && currentEnd > bestEnd) {maxLength = currentLengthbestStart = ibestEnd = currentEnd}}}// 输出结果if maxLength >= 5 {chain := strings.Join(order[bestStart:bestEnd+1], "-")fmt.Println(chain)} else {fmt.Println("NO-CHAIN")}
}
代码详细解析
-
输入处理:
- 使用
bufio.Scanner读取输入的两行数据。 - 合并手牌和已出牌,分割为数组
allCards。
- 使用
-
有效牌定义:
order := []string{"3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K", "A"}- 明确有效牌的顺序,用
map快速判断合法性。
- 明确有效牌的顺序,用
-
统计剩余次数:
remain := make(map[string]int) for _, card := range order {remain[card] = 4 - count[card] }- 计算每张牌的剩余次数(4 - 已用次数)。
-
滑动窗口遍历:
- 外层循环遍历每个可能的起始点
i。 - 内层循环从
i向右扩展,直到遇到剩余为0的牌。 - 记录窗口的结束位置
currentEnd。
- 外层循环遍历每个可能的起始点
-
结果选择:
- 如果当前窗口长度大于历史最大值,或长度相同但结束位置更大,则更新最优解。
-
输出结果:
- 生成顺子字符串或输出
NO-CHAIN。
- 生成顺子字符串或输出
示例测试
示例1输入:
3-3-4-4-5-A-5-6-2-8-3-9-10-Q-7-K-J-10-B
A-4-5-8-8-10-C-6-7-8
输出:
9-10-J-Q-K-A
解析:剩余牌中 9,10,J,Q,K,A 连续可用,形成最长顺子。
示例2输入(无顺子):
3-3-3-3
4-4-4-4
输出:
NO-CHAIN
解析:所有牌剩余次数为0,无法组成顺子。
示例3输入(最长顺子):
3-4-5-6-7-8-9-10-J-Q-K-A
(空已出牌)
输出:
3-4-5-6-7-8-9-10-J-Q-K-A
综合分析
-
时间复杂度:
- 输入处理:O(n),n为输入牌数量。
- 滑动窗口遍历:O(12²) = O(144),高效处理小规模数据。
-
空间复杂度:
- 统计存储:O(12),存储剩余次数和牌顺序。
-
优势:
- 严格顺序遍历:保证找到最长且最大的顺子。
- 高效剪枝:遇到不可用牌立即停止扩展。
-
适用场景:
- 输入规模小(题目约束),适合滑动窗口法。
更多内容:
https://www.kdocs.cn/l/cvk0eoGYucWA
本文发表于【纪元A梦】,关注我,获取更多实用教程/资源!
相关文章:

华为OD机试真题——最长的顺子(2025A卷:100分)Java/python/JavaScript/C++/C语言/GO六种最佳实现
2025 A卷 100分 题型 本文涵盖详细的问题分析、解题思路、代码实现、代码详解、测试用例以及综合分析; 并提供Java、python、JavaScript、C、C语言、GO六种语言的最佳实现方式! 本文收录于专栏:《2025华为OD真题目录全流程解析/备考攻略/经验…...

【HTML】html文件
HTML文件全解析:搭建网页的基石 在互联网的广袤世界里,每一个绚丽多彩、功能各异的网页背后,都离不开HTML文件的默默支撑。HTML,即超文本标记语言(HyperText Markup Language),作为网页创建的基…...

使用 XWPFDocument 生成表格时固定列宽度
一、XWPFDocument XWPFTable个性化属性 1.初始默认写法 XWPFTable table document.createTable(n, m); //在文档中创建一个n行m列的表格 table.setWidth("100%"); // 表格占页面100%宽度// 通过getRow获取行进行自定义设置 XWPFTableRow row table.getRow(0); XW…...

足球AI模型:一款用数据分析赛事的模型
2023 年欧冠决赛前,某体育数据平台的 AI 模型以 78% 的概率预测曼城夺冠 —— 最终瓜迪奥拉的球队首次捧起大耳朵杯。当足球遇上 AI,那些看似玄学的 "足球是圆的",正在被数据与算法拆解成可计算的概率命题。今天我们就来聊聊&#…...

【ESP32|音频】一文读懂WAV音频文件格式【详解】
简介 最近在学习I2S音频相关内容,无可避免会涉及到关于音频格式的内容,所以刚开始接触的时候有点一头雾水,后面了解了下WAV相关内容,大致能够看懂wav音频格式是怎么样的了。本文主要为后面ESP32 I2S音频系列文章做铺垫࿰…...

万向死锁的发生
我是标题 1.欧拉角2.万向死锁 参考:小豆8593 1.欧拉角 欧拉角在Unity中描述的是一种变换(Transform)共有3个轴体,默认顺序为x->y->z. 2.万向死锁 可以把万向死锁的情况理解成:由于轴体旋转的顺序是固定的&am…...
 详解(18))
JavaScript学习教程,从入门到精通,JavaScript BOM (Browser Object Model) 详解(18)
JavaScript BOM (Browser Object Model) 详解 1. BOM 介绍 BOM (Browser Object Model) 是浏览器对象模型,它提供了独立于内容而与浏览器窗口进行交互的对象。BOM的核心对象是window,它表示浏览器的一个实例。 BOM包含的主要对象: window…...

人工智能与云计算:技术融合与实践
1. 引言 人工智能(AI)和云计算是当今科技领域最具变革性的两项技术。AI通过模拟人类智能解决问题,而云计算则提供了弹性可扩展的计算资源。两者的结合创造了前所未有的可能性,使企业能够以更低的成本部署复杂的AI解决方案。 本文将探讨AI与云计算的技术融合,包括核心概念、…...

42.[前端开发-JavaScript高级]Day07-手写apply-call-bind-块级作用域
手写apply-call-bind <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevi…...

ObjectInputStream 终极解析与记忆指南
ObjectInputStream 终极解析与记忆指南 一、核心本质 ObjectInputStream 是 Java 提供的对象反序列化流,继承自 InputStream,用于读取由ObjectOutputStream序列化的Java对象。 核心特性速查表 特性说明继承链InputStream → ObjectInputStream核心功能实现Java对象反序列化…...
)
数据结构有哪些类型(对于数据结构的简述)
在学习计算机时,数据结构是不可忽视的一点,从考研时的408课程,再到工作中编写软件,网站,要想在计算机领域站住脚跟,数据结构是必备的 在这里,我对于数据结构进行了汇总,并简要描述&…...

Vscode 插件开发
文章目录 1、使用vscode官方插件生成框架,下载脚手架2、使用脚手架初始化项目,这里我选择的是js3、生成的文件结构如下,重要的就是以下两个文件4、代码5、打包使用6、发布官网地址7、publisher ID undefined provided in the extension manif…...

C# string和其他引用类型的区别
在C#中,字符串(String)和其他引用类型(Reference Types)之间有几个关键的区别,这些区别主要体现在它们的内存管理、赋值行为以及使用方式上。 1. 内存管理 字符串(String)࿱…...

RTT添加一个RTC时钟驱动,以DS1307为例
添加一个外部时钟芯片 这里多了一个选项 复制drv_rtc.c,重命名为drv_rtc_ds1307.c 添加到工程中 /*** @file drv_rtc_ds1307.c* @brief * @author jiache (wanghuan3037@fiberhome.com)* @version 1.0* @date 2025-01-08* * @copyright Copyright (c) 2025 58* */ #...
常见的低代码策略整理
低代码策略通过简化开发流程、降低技术门槛、提升效率,帮助用户快速构建灵活可靠的应用。这些策略的核心优势体现在以下方面: 快速交付与降本增效 减少编码需求:通过可视化配置(如变量替换、表达式函数)替代传统编码…...

从彩色打印单行标准九九表学习〖代码情书〗的书写范式(Python/DeepSeek)
写给python终端的情书,学习代码设计/书写秘笈。 笔记模板由python脚本于2025-04-17 12:49:08创建,本篇笔记适合有python编程基础的coder翻阅。 【学习的细节是欢悦的历程】 博客的核心价值:在于输出思考与经验,而不仅仅是知识的简…...

QML与C++:基于ListView调用外部模型进行增删改查(附自定义组件)
目录 引言相关阅读项目结构文件组织 核心技术实现1. 数据模型设计联系人项目类 (datamodel.h)数据模型类 (datamodel.h)数据模型实现 (datamodel.cpp) 2. 主程序入口点 (main.cpp)3. 主界面设计 (Main.qml)4. 联系人对话框 (ContactDialog.qml)5. 自定义组件CustomTextField.qm…...

postman莫名奇妙报错,可能是注释引起的。postman 过滤请求体中的注释。
postman莫名奇妙报错,可能是注释引起的。postman 过滤请求体中的注释。 1、问题描述2、问题分析3、解决方法 1、问题描述 postman http请求测试时,如果在请求体中添加了注释,那么这个注释会被带到服务端执行,导致服务端接口返回报…...

扩增子分析|基于R语言microeco包进行微生物群落网络分析(network网络、Zi-Pi关键物种和subnet子网络图)
一、引言 microeco包是福建农林大学姚敏杰教授团队开发的扩增子测序集成分析。该包综合了扩增子测序下游分析的多种功能包括群落组成、多样性、网络分析、零模型等等。通过简单的几行代码可实现复杂的分析。因此,microeco包发表以来被学界广泛关注,截止2…...

中间件--ClickHouse-4--向量化执行(什么是向量?为什么向量化执行的更快?)
1、向量(Vector)的概念 (1)、向量的定义 向量:在计算机科学中,向量是一组同类型数据的有序集合,例如一个包含多个数值的数组。在数据库中,向量通常指批量数据(如一列数…...
)
TDengine 存储引擎剖析:数据文件与索引设计(一)
TDengine 存储引擎简介 在物联网、工业互联网等快速发展的今天,时间序列数据呈爆发式增长。这些数据具有产生频率高、依赖采集时间、测点多信息量大等特点,对数据存储和处理提出了极高要求。TDengine 作为一款高性能、分布式、支持 SQL 的时序数据库&am…...

【kubernetes】pod.spec.containers.ports的介绍
目录 1. 说明2. 基本结构3. 字段说明4. 使用场景5. 示例6. 注意事项 1. 说明 1.在 Kubernetes 中,pod.spec.containers.ports 是 Pod 定义中用于配置容器端口映射的字段,其作用是声明容器需要监听的端口以及如何将这些端口暴露给 Pod 的外部访问。 2. …...

【SpringBoot+Vue自学笔记】001
跟着这位老师学习的:https://www.bilibili.com/video/BV1nV4y1s7ZN?vd_sourceaf46ae3e8740f44ad87ced5536fc1a45 前后端开发技术的全栈课程: Java EE企业级框架:SpringBootMyBatisPlus Web前端核心框架:VueElement UI 公共云…...
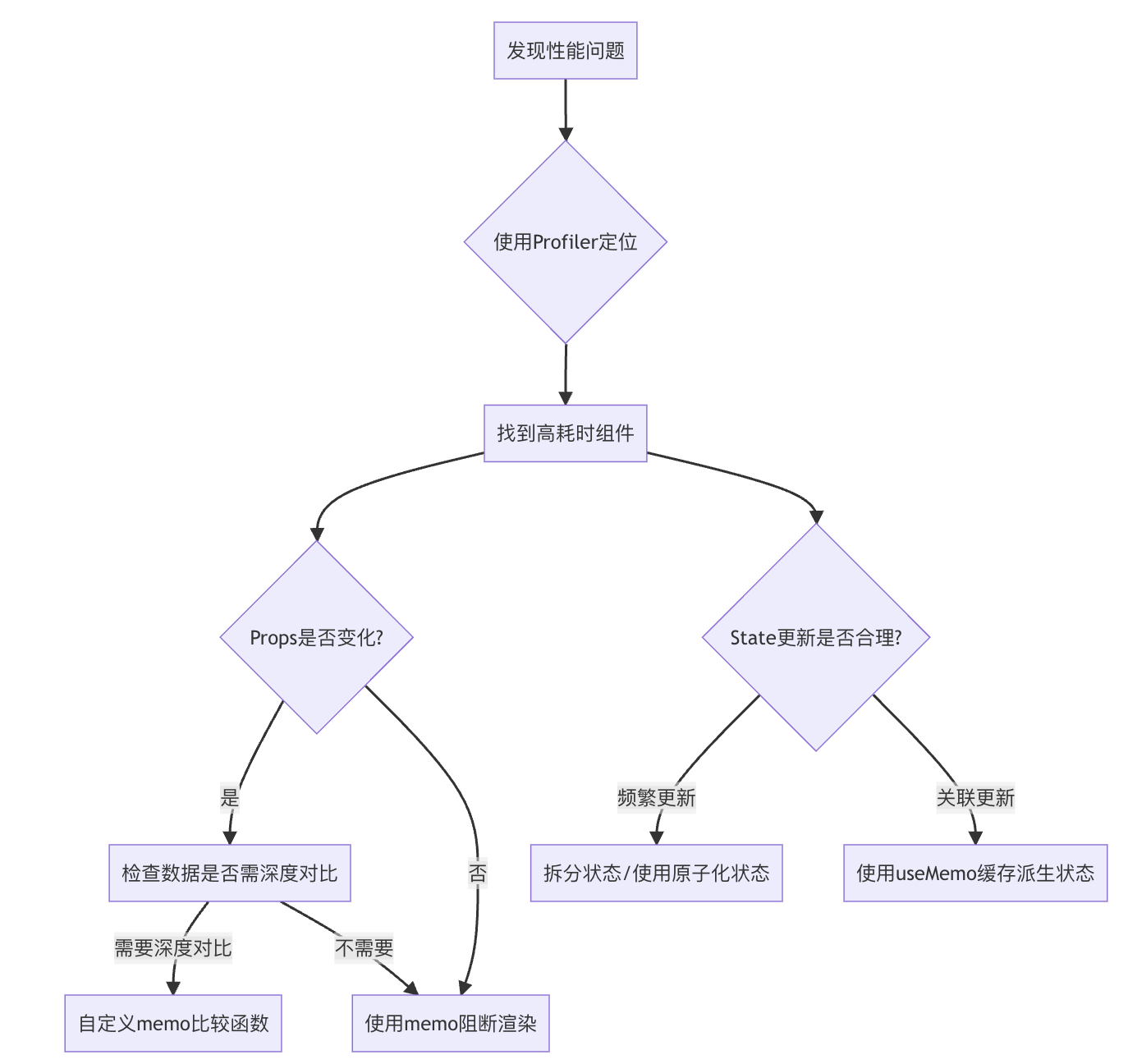
第十节:性能优化-如何排查组件不必要的重复渲染?
工具:React DevTools Profiler 方法:memo、shouldComponentUpdate深度对比 React 组件性能优化:排查与解决重复渲染问题指南 一、定位性能问题:React DevTools 高级用法 使用 React Developer Tools Profiler 精准定位问题组件&…...

MATLAB项目实战(一)
题目: 某公司有6个建筑工地要开工,每个工地的位置(用平面坐标系a,b表示,距离单位:km)及水泥日用量d(t)由下表给出.目前有两个临时料场位于A(5,1),B(2,7),日储…...

spring boot 文件下载
1.添加文件下载工具依赖 Commons IO is a library of utilities to assist with developing IO functionality. <dependency><groupId>commons-io</groupId><artifactId>commons-io</artifactId><version>2.6</version> </depe…...

HTTP 2.0 协议特性详解
1. 使用二进制协议,简化传输的复杂性,提高了效率 2. 支持一个 TCP 链接发起多请求,移除 pipeline HTTP/2 移除了 HTTP/1.1中的管道化(pipeline)机制,转而采用多路复用(Multiplexing࿰…...

微服务链路追踪:SleuthZipkin
文章目录 Sleuth & Zipkin一、Sleuth\&Zipkin介绍二、搭建环境三、Sleuth入门操作四、Zipkin搭建及操作五、RabbitMQ方式发送信息六、Elasticsearch持久化 SpringBootAdmin一、Actuator介绍二、Actuator快速入门三、SpringBootAdmin介绍四、SpringBootAdmin快速入门4.1…...

HTML语义化与无障碍设计
HTML 语义化与无障碍设计:构建包容且高效的网页体验 引言 在我的前端开发学习旅程中,起初将 HTML 仅视为页面布局的工具,大量使用无语义的 <div> 和 <span>。直到在一篇技术博客当中了解到,作者在一次团队项目中&am…...

java面试篇 4.9(mybatis+微服务+线程安全+线程池)
目录 mybatis: 1、mybatis的执行流程 2、mybatis是否支持延迟加载? 当我们需要去开启全局的懒加载时: 3、mybatis的一级和二级缓存 微服务 1、springcloud五大组件有哪些 2、服务注册和发现是什么意思?springcloud如何实现…...
