无约束最优化问题的求解算法--梯度下降法（Gradient Descent）

梯度下降法

• 梯度下降法（Gradient Descent）：是一个非常通用的优化算法帮助机器学习求解最优解。所有优化算法的目的都是期待以最快的速度求解模型参数θ，梯度下降就是一种经典常用的优化算法。
• 使用梯度下降法的原因：
  • 如果机器学习的损失函数是非凸函数，使用解析解公式求解θ，设置梯度为0会得到很多极值，甚至可能是极大值。
  1. 解析解计算成本高 ：当特征维度N较大时，解析解需要计算矩阵的逆（复杂度O(N³)），计算时间呈指数级增长。例如，特征数量从4增加到16，计算时间会从1秒暴增到64秒。
  2. 更适合高维和大规模数据：梯度下降法通过迭代逼近最优解，避免了直接求逆的计算瓶颈，尤其适合特征维度高或数据量大的场景（如深度学习）。
  3. 动态优化的优势：解析解需要一次性求解，而梯度下降可以逐步优化，灵活适应在线学习或超大规模数据的分批训练。

---

梯度下降法原理（通俗版）

1. 初始化：随机猜一个起点：就像猜工资时先随便说个数，计算机一开始也会随机给参数θ（比如W₁, W₂…Wₙ）赋一组初始值。
2. 计算误差（Loss）：用当前的θ预测结果（ŷ），并计算预测值ŷ和真实值y的差距（比如用均方误差MSE）。 目标：让这个误差越小越好。
3. 调整参数：根据反馈改进：如果误差变小了：说明调整方向正确，继续按这个方向微调θ；如果误差变大了：说明调反了，换个方向调整（比如增大改减小，或反之）。
4. 重复直到最优：像“道士下山”一样，一步步试探，最终找到误差最低的θ（山谷最低点）。

• 核心思想**“猜-反馈-改进”循环**，通过不断试错逼近最优解，而不是直接计算复杂公式。

---

类比简化

• 猜工资游戏： 朋友说“高了/低了”，你逐步逼近正确答案。
• 梯度下降：计算机用“误差”反馈（如MSE）指导参数调整方向，直到最优。

梯度下降法公式

• 参数更新公式：
  $$W_j^{(t+1)}=W_j^{(t)}-\eta \cdot {\text{gradient}}_j$$
• 符号说明：
  • $W_j^{(t)}$：第 $t$轮迭代时的参数$W_j$（$\theta$ 中的一个分量）。
  • $\eta$（或$\alpha$）：学习率（learning rate），控制每次调整的步长（类似“下山时的步幅”）。
  • ${\text{gradient}}_j$：损失函数对 $W_j$的梯度（即当前方向上的“最陡下降方向”）。

核心作用：

• 梯度（gradient） 告诉参数“往哪个方向调整能最快降低误差”。
• 学习率（η） 决定调整的幅度：
  • η太大 → 可能“跨过”最优解（震荡甚至发散）。
  • η太小 → 收敛慢（下山速度太慢）。
    
    关键点：

1. 梯度决定方向（往哪走），学习率决定步幅（走多远）。
2. 所有参数$W_j$同时按各自梯度调整，直到收敛。

---

• 公式的直观意义：“沿着梯度方向，迈一小步，反复走，直到最低点。”
  $$\text{新参数}=\text{旧参数}-\text{步长}\times \text{最陡方向}$$

学习率的设置

• 权重更新公式：$W_j^{t+1}=W_j^t-\eta \cdot {\text{gradient}}_j$
  • $W_j^t$：当前权重
  • $\eta$（eta）：学习率（控制每次调整的幅度）
  • ${\text{gradient}}_j$：损失函数对权重的梯度
    
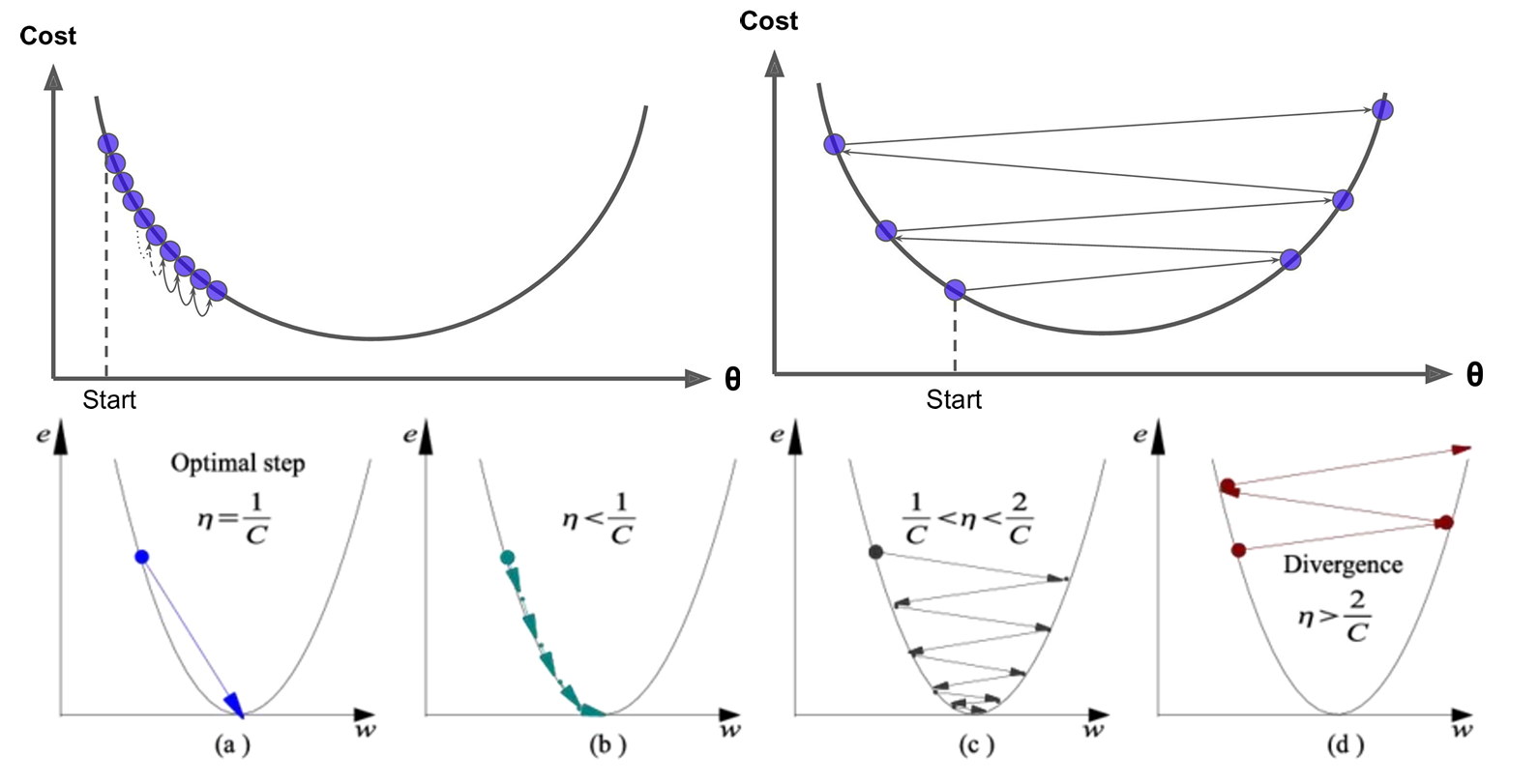
• 学习率的影响
  1. 学习率太大（如 η=1.0）：调整幅度过大，容易“跨过”最优解，导致震荡甚至无法收敛。类似“步子太大，容易走过头，来回摇摆”。
  2. 学习率太小（如 η=0.0001）：每次调整幅度过小，收敛速度极慢，训练时间大幅增加。类似“小碎步前进，要走很久才能到达目标”。

如何选择学习率？

✅ 常用初始值：0.1、0.01、0.001、0.0001（根据问题调整）
✅ 动态调整策略：

• 学习率衰减：随着训练进行，逐步减小 η（越接近最优解，步伐越小）。
• 自适应优化算法：如 Adam、RMSprop 等，自动调整学习率。
  

全局最优解

• 如果损失函数是非凸函数，梯度下降法是有可能落到局部最小值的，所以其实步长不能设置的太小太稳健，那样就很容易落入局部最优解，虽说局部最小值也没大问题，因为模型只要是堪用的就好嘛，但是我们肯定还是尽量要奔着全局最优解去。

梯度下降法流程

• 梯度下降法就像一个人蒙着眼睛下山的过程，通过不断试探找到最低点。
• 以下是具体步骤：

1. 随机初始化：先随便猜一组参数值（θ或W），就像随机站在山上的某个点。
   • 实现方法：np.random.rand()或np.random.randn()
2. 计算梯度：计算当前位置的"坡度"（梯度）。梯度是损失函数在该点的斜率，指向最陡上升方向。
   • 关键点：梯度指向上升方向，所以我们要往反方向走才能下降。
3. 参数更新：
   • 如果梯度(g)为负 → 需要增大θ
   • 如果梯度(g)为正 → 需要减小θ
   • 更新公式：${\theta }_{new}={\theta }_{old}-\eta \times gradient$ （η是学习率，控制步长）
4. 判断收敛：
   • 不能简单判断梯度=0（可能是局部最低或最高点）
   • 更好的方法是观察损失值的变化：当损失值基本不再下降时停止
   • 实际做法：设置阈值，当损失变化小于阈值时停止

• 关键问题
  1. 如何随机初始化？：使用随机函数生成初始参数值
  2. 如何计算梯度？：需要求损失函数对各个参数的偏导数（这是后续要详细讲解的部分）
  3. 如何调整参数？：按照公式：新参数 = 旧参数 - 学习率×梯度
  4. 如何判断收敛？：监测损失值的变化幅度，而不是梯度本身

损失函数的导函数

• 推导损失函数的导函数
  
• $J(\theta )$是损失函数
• ${\theta }_j$是某个特征维度$X_j$对应的权值系数
• 损失函数是MSE，MSE中x、y是已知的，θ是未知的，而θ不是一个变量而是一堆变量。所以我们只能对含有一推变量的函数MSE中的一个变量求导，即偏导，下面就是对${\theta }_j$求偏
  导。
  
  

三种梯度下降法

---

梯度下降法核心步骤回顾

1. 初始化参数：随机生成初始参数（θ/W）。
2. 计算梯度：求损失函数对参数的偏导（梯度），确定下降方向。
3. 更新参数：沿梯度反方向调整参数（学习率η控制步长）。
4. 判断收敛：通过损失变化或梯度接近零终止迭代。

---

优缺点详解

1. 全量梯度下降 (Batch Gradient Descent, BGD)

• 公式：
  $${\theta }_j^{t+1}={\theta }_j^t-\eta \cdot \frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j^{(i)}$$
  说明：
• ${\theta }_j^t$: 第 $t$ 次迭代的参数${\theta }_j$（第$j$ 维）。
• $\eta$: 学习率（步长）。
• $m$: 训练集总样本数。
• $h_{\theta }(x^{(i)})$: 模型对样本$x^{(i)}$的预测值。
• 特点：每次迭代使用全部样本计算梯度，更新稳定但计算成本高。
• 优点：
  • 梯度方向准确，收敛稳定（数学上保证凸函数的全局最优）。
  • 易于并行化（因梯度计算依赖全数据集）。
• 缺点：
  • 计算成本高（每次迭代需遍历全部数据）。
  • 内存占用大，无法处理超出内存的数据集。
  • 对非凸函数可能陷入局部最优。

2. 随机梯度下降 (Stochastic Gradient Descent, SGD)

公式：
$${\theta }_j^{t+1}={\theta }_j^t-\eta \cdot \left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j^{(i)}$$
说明：

• $i$: 随机选取的单个样本索引（$i\sim \text{Uniform}(1,m)$）。
• 特点：每次迭代仅用一个样本更新参数，计算快但噪声大。
• 优点：
  • 计算速度快，适合大规模或流式数据。
  • 随机性可能逃离局部最优（非凸优化中表现更好）。
• 缺点：
  • 梯度估计噪声大，收敛不稳定（需精细调节学习率）。
  • 难以并行化（因更新依赖单个样本）。

3. 小批量梯度下降 (Mini-Batch Gradient Descent, MBGD)

公式：
$${\theta }_j^{t+1}={\theta }_j^t-\eta \cdot \frac{1}{b}\sum _{i=k}^{k+b-1}\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j^{(i)}$$
说明：

• $b$: 小批量大小（通常$b\in [32,256]$）。
• $k$: 当前批次的起始样本索引。
• 特点：折中方案，平衡计算效率和稳定性。
• 优点：
  • 平衡BGD的稳定性和SGD的速度（主流深度学习选择）。
  • 可利用GPU并行计算小批量数据。
• 缺点：
  • 需手动调节批量大小（k）和学习率。
  • 仍存在一定噪声（但比SGD小）。

---

收敛路径：
BGD  → 平滑但慢  
SGD  → 快速但震荡  
MBGD → 折中方案

---

三种梯度下降的区别与对比

类型	全量（批量）梯度下降 (BGD)	随机梯度下降 (SGD)	小批量梯度下降 (MBGD)
每次迭代的样本量	全部样本（N）	单个样本（1）	小批量样本（k，通常32-256）
梯度计算方式	真实梯度（全局平均）	噪声梯度（单个样本的估计）	近似梯度（局部平均）
参数更新频率	每轮迭代1次更新	每样本1次更新	每k个样本1次更新
收敛性	稳定，但可能陷入局部最优	不稳定，震荡大	平衡稳定性和随机性
计算效率	慢（尤其大数据集）	快（适合在线学习）	适中（GPU并行优化友好）
内存需求	高（需加载全部数据）	低	中
适用场景	凸函数、小数据集	非凸优化、大规模数据	深度学习等大多数场景

---

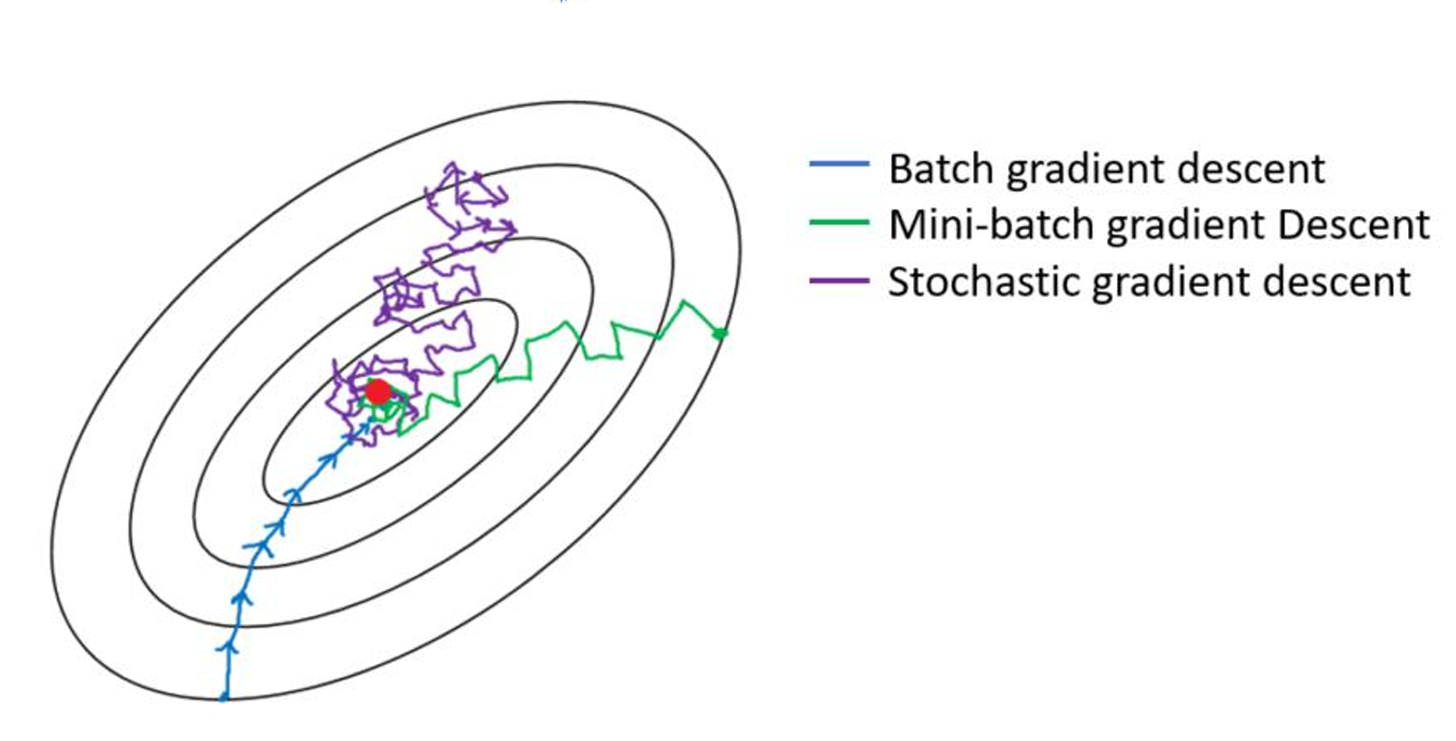
如何选择？

• 数据量小 → BGD（确保精度）。
• 数据量大/在线学习 → SGD（牺牲稳定性换速度）。
• 深度学习/默认推荐 → MBGD（批量大小常选32/64/128）。

---

梯度下降法的问题与挑战