算法-堆+单调栈
堆
首先堆在我们的Java中我们的是一个优先队列类
PriorityQueue
然后我们要弄最大堆和最小堆
最大堆:
PriorityQueue<Integer> pq = new PriorityQueue<Integer>((a, b) -> b - a);
最小堆:
PriorityQueue<Integer> pq = new PriorityQueue<Integer>((a, b) -> a-b);
1046最后一块石头的重量
我们让最大的和第二大的石头相撞,我们就能得到最小的结果
所以我们维护一个最大堆
PriorityQueue<Integer> pq = new PriorityQueue<Integer>((a, b) -> b - a);

2558从数量最多的堆取走礼物

3264K次乘数运算后的最终数组
我们还有一种思路是
我们往堆里面存的类型是数组
ProityQueue<int[]>
然后【0】是我们的值
【1】是我们的这个元素的下标
两个元素按值的大小排序,当值相同是按照谁的下标靠前来排序
PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> a[0] != b[0] ? a[0]-b[0] : a[1]-b[1]);
2530执行k次操作后的最大分数

单调栈
739每日温度
我们遇到第一个不是递增的温度的时候,我们前面的节点计算就结束了
所以我们用个栈,来存我们的单调递增的天的下标
然后用变量i,来往后遍历
当遇到我们的第一个不是递增的温度时
我们用 当前变量i减去栈中天的下标
然后把距离差记录到我们的数组里

1475商品折扣后的最终价格
我们的栈是从右往左收集的

看看我们的收集情况和弹出情况
收集:
我们从右往左进行收集我们的元素的值
弹出情况:
如果我们遍历到i这个位置,我们的price【i】比我们栈元素大
说明我们不能打折,我们要右边小于左边才能打折
所以我们不断弹出,直到遇见第一个比我们小的数字,如果stack为空那就是不打折,不为空那就是打折
ps:如果右边弹出完,然后继续遍历左边的值是否有影响?因为我们用不到数组右边那一大段了
不会,因为我们能弹出,就是因为当前元素比栈元素小,
所以当前元素又是最靠左,又比之前栈里的元素小,所以之前右边的元素弹出没有用到就无所谓了

503下一个更大元素

962最大宽度坡


我们首先维护一个单调递减的栈
然后把我们单调递减的值对应的下标放到我们的栈里面
然后我们要求最远距离
所以我们就从右往左进行遍历
为啥一满足条件,就把栈里的元素弹出呢?
因为我们最右边,肯定才是最远的,我们从右往左遍历,最右边那个值n和i的位置的差值
肯定比n-1和i位置的差值大
所以栈里的这个元素的位置,已经没必要使用了
853车队
首先我们要有个Time【】数组,记录各个位置到终点target的时间(起始的时候,每个位置只有一辆车)
然后我们用一个栈来维护我们的结果
因为我们是从地点0往地点target开始遍历的,
所以我们在前面的地点,遇到比我们花费时间久的,也就是我前面地点的Time花费比我后面地点的Time多
就说明他会卡住我们,形成一个车队
所以我们把栈里的pop出,把这个前面的慢车+进去
遇到前面比我们花费时间少的,加进去
说人话,
time【i】>栈里车耗费的时间
我们就把栈里的弹出来,然后把i这个位置的车当作一个组放进去
time【i】<栈里车耗费的时间
说明我们追不上前面,我们把它当作一个组放进去

1124表现良好的最长时间段

前缀知识:前缀和

单调栈解法
劳累天的值为1
不劳累天的值为-1
然后我们要求和>1的最长子数组

看看代码
我们计算前缀和
然后维护一个前缀和单调递减的栈,栈里面存的是我们位置的下标
(说一下为什么我们的栈要单调递减,跳过的比它大的元素怎么办
首先我们的栈是从左往右遍历,而我们的差值的计算是从右往左
例如
3 5 2 1 4
3 5 2 1 6
我们的栈里面是【3,2,1】为啥5没用呢,因为我们从右往左遍历我们遇到的数字有这样的情况
nums【j】>3但是nums【j】<5 这样子的情况,我们就不用考虑5 例如第一个例子 4>3 4<5
nums【j】>5>3 考虑5的情况,也明显是左边的3更远,所以5根本没用 第二个例子 6>5>3
所以单调递减栈外那些比我们栈内元素值大的元素我们都没必要去考虑,你看我们分析的情况下那值对我们根本没影响
)
然后我们从后往前遍历,来算两个位置之间的差值,然后我们的ans保存差值的最大值

(重要)132模式
我们的位置是 i <j <k
然后我们要求的是
nums【j】>nums【k】>nums【i】

其实我们也想到了,这个就是枚举而已,但是我们要枚举哪个好一点呢?
如何在确定一个数后快速找到另外两个数
枚举 i:
由于 i 是 132 结构中最小的数,那么相当于我们要从 i 后面,找到一个对数 (j,k),使得 (j,k) 都满足比 i 大,同时 j 和 k 之间存在 j > k 的关系。由于我们的遍历是单向的,因此我们可以将问题转化为找 k,首先 k 需要比 i 大,同时在 [i, k] 之间存在比 k 大的数即可。
枚举 j:
由于 j 是 132 结构里最大的数,因此我们需要在 j 的右边中比 j 小的「最大」的数,在 j 的左边找比 j 小的「最小」的数。这很容易联想到单调栈,但是朴素的单调栈是帮助我们找到左边或者右边「最近」的数,无法直接满足我们「最大」和「最小」的要求,需要引入额外逻辑。
枚举 k:
由于 k 是 132 结构中的中间值,这里的分析逻辑和「枚举 i」类似,因为遍历是单向的,我们需要找到 k 左边的 i,同时确保 [i,k] 之间存在比 i 和 k 大的数字

开始我们的答案解析

处理过程:
我们从后往前做,维护一个「单调递减」的栈,同时使用 k 记录所有出栈元素的最大值(k 代表满足 132 结构中的 2)
我们从后往前进行遍历
我们出栈的条件是nums【i】>deque.peeLast()
如果我们的K有值的话,就说明我们满足了(J>K)
看看我们的K的逻辑
我们是单调栈不满足单调递减的时候弹出,此时我们的K才有值,不满足单调递减说明我们已经找到了(J>K)所以我们后面就剩找K>i了
这就是为啥我们的nums【i】<k的时候我们return true

矩形面积
42接雨水

相关文章:

算法-堆+单调栈
堆 首先堆在我们的Java中我们的是一个优先队列类 PriorityQueue 然后我们要弄最大堆和最小堆 最大堆: PriorityQueue<Integer> pq new PriorityQueue<Integer>((a, b) -> b - a); 最小堆: PriorityQueue<Integer> pq new P…...

物联网平台管理系统
物联网平台管理系统概述 物联网平台管理系统是物联网架构中的核心枢纽,承担着承上启下的关键作用。它向下连接各类物联网设备,实现设备的接入、管理与控制;向上为应用开发提供统一的数据接口和共性模块工具,支撑起各种丰富多彩的…...

STM32CubeMX-H7-15-SPI通信协议读写W25Q64
前言 SPI(Serial Peripheral Interface)通信协议是一种高速、全双工、同步的串行通信协议 本篇文章就使用W25Q64模块来学习SPI,包括软件SPI代码的编写,硬件SPI,中断SPI和DMASPI SPI的应用场景和模块 !这里是抄AI的&a…...

【软考】论devops在企业信息系统开发中的应用
摘要: 随着互联网的不断发展,各行各业都在建设自己的企业信息系统,而随着业务的不断升级和复杂化,系统的更新迭代速度越来越快,系统也越来越复杂。对于信息系统开发者,架构师,管理者,…...

生物化学笔记:医学免疫学原理22 肿瘤及肿瘤治疗
肿瘤及肿瘤治疗 免疫疗法 CAR-T细胞介绍...

JVM考古现场(二十二):降维打击·用二向箔优化内存模型
"警报!三维堆内存正在经历二维化坍缩!" 我腰间的玄铁令突然震动,在蜀山剑派的量子剑阵中投射出诡异的曼德博分形——这是三体文明发动降维打击的铁证! 楔子:二向箔奇点降临 昆仑镜监控日志: // …...

第三阶段面试题
Nginx nginx常用模块以及其功能 proxy模块,进行代理功能 ssl模块,进行HTTPS协议的使用 gzip模块,进行传输数据的压缩 upstream模块,进行反向代理时使用 static模块,静态资源进行访问的模块 cache模块࿰…...

操作系统-PV
🧠 背景:为什么会有 PV? 类比:内存(生产者) 和 CPU(消费者) 内存 / IO / 磁盘 / 网络下载 → 不断“生产数据” 例如:读取文件、下载视频、从数据库加载信息 CPU → 负…...

nuxt3路由切换页面出不来,刷新可以
nuxt3遇到一个奇怪的现象: 不管是router.push()跳转还是navigateTo()跳转,浏览器url变了,但是页面是空白的,没加载出来,刷新之后页面正常。 解决方案: <template>下的所有内容必须套在一个div里面...

Spring Boot配置文件优先级全解析:如何优雅覆盖默认配置?
📚 一、为什么需要了解配置文件优先级? 想象一下,你正在玩一个游戏🎮,游戏里有默认设置,但你可以通过不同的方式修改这些设置: 游戏内置的默认设置(就像Spring Boot的默认配置&…...

医院数据中心智能化数据上报与调数机制设计
针对医院数据中心的智能化数据上报与调数机制设计,需兼顾数据安全性、效率性、合规性及智能化能力。以下为系统性设计方案,分为核心模块、技术架构和关键流程三部分: 一、核心模块设计 1. 数据上报模块 子模块功能描述多源接入层对接HIS/LIS/PACS/EMR等异构系统,支持API/E…...

Linux之基础命令
Linux作为开源操作系统的代表,以其高效、灵活和强大的命令行工具闻名。无论是系统管理、开发调试还是日常使用,掌握基础命令都是与Linux系统交互的必备技能。本文整理了20个最常用的Linux基础命令,帮助新手快速入门。 目录 目录与文件导航文…...

【MATLAB代码例程】AOA与TOA结合的高精度平面地位,适用于四个基站的情况,附完整的代码
本代码实现了一种基于到达角(AOA) 和到达时间(TOA) 的混合定位算法,适用于二维平面内移动或静止目标的定位。通过4个基站的协同测量,结合最小二乘法和几何解算,能够有效估计目标位置,并支持噪声模拟、误差分析和可视化输出。适用于室内定位、无人机导航、工业监测等场景…...

PC主板及CPU ID 信息、笔记本电脑唯一 MAC地址获取
🥇 版权: 本文由【墨理学AI】原创首发、各位读者大大、敬请查阅、感谢三连 🎉 声明: 作为全网 AI 领域 干货最多的博主之一,❤️ 不负光阴不负卿 ❤️ 文章目录 PC主板及CPU ID 信息物理 MAC地址获取win11 新电脑 wmic 安装❤️ 欢迎一起学AI…...

RK3568笔记八十二: 利用AI生成的简单数据转发服务程序
若该文为原创文章,转载请注明原文出处。 测试AI编写代码能力,做了个简单的数据转发功能,后期想部署到服务器 功能相对简单,大概功能如下: 1、打开TCP服务端,等待客户端连接 2、客户端连接后发送ID:1234格式,服务端收到,解析出ID:1234并记录 3、相同的ID数据之间互…...

C++17 信号量模拟实现
C17 信号量模拟实现 一、实现原理 C17 标准库没有原生信号量(C20才有),但可以通过 std::mutex std::condition_variable 模拟实现。以下是核心逻辑: #include <mutex> #include <condition_variable>class CountingSemaphore { private:…...

web后端语言中篇
#作者:允砸儿 #日期:乙巳青蛇年 三月十八 笔者本来打算隔一天给它更完的,但是事情有点多这几天,实在是抱歉。废话不多说直接进入正题。 PHP流程控制语句 什么是流控:流程控制语句用于决定代码的执行顺序。 #注意流程控制语句…...

Spine-Leaf 与 传统三层架构:全面对比与解析
本文将详细介绍Spine-Leaf架构,深入对比传统三层架构(Core、Aggre、Access),并探讨其与Full-mesh网络和软件定义网络(SDN)的关联。通过通俗易懂的示例和数据中心网络分析,我将帮助您理解Spine-L…...

Vmware esxi 查看硬盘健康状况
起因 硬盘掉盘 - - 使用自带的命令esxcli 列出所有硬盘 esxcli storage core device list[rootlocalhost:~] esxcli storage core device list t10.NVMe____INTEL_MEMPEK1W016GAL____________________PHBT83660BYP016D____00000001Display Name: Local NVMe Disk (t10.NVMe…...

React 事件处理基础
React 中最常见的两个需求,一个是列表渲染,另一个就是绑定点击事件。 这一篇就是从最基础的按钮点击开始,分四个阶段,逐步理解 React 中事件的写法和参数传递方式。 📍阶段一:最简单的点击事件 function A…...

pandas库详解
CONTENT 基本数据结构SeriesDataFrame 数据读取与写入读取 CSV 文件写入 CSV 文件 数据清洗处理缺失值数据类型转换 数据操作索引与切片数据合并数据分组与聚合 数据可视化 基本数据结构 Series Series 属于一维标记数组,由一组数据和对应的索引构成。 import pa…...

焊接机器人的设计
一、引言 随着制造业的发展,焊接工艺在各个领域得到广泛应用。焊接机器人具有焊接质量高、效率高、劳动强度低等优点,能够满足现代制造业对焊接生产的要求。设计一款性能优良的焊接机器人,对于提高焊接生产的自动化水平和产品质量具有重要意…...

python进阶: 深入了解调试利器 Pdb
Python是一种广泛使用的编程语言,以其简洁和可读性著称。在开发和调试过程中,遇到错误和问题是不可避免的。Python为此提供了一个强大的调试工具——Pdb(Python Debugger)。 Pdb是Python标准库中自带的调试器,可以帮助…...
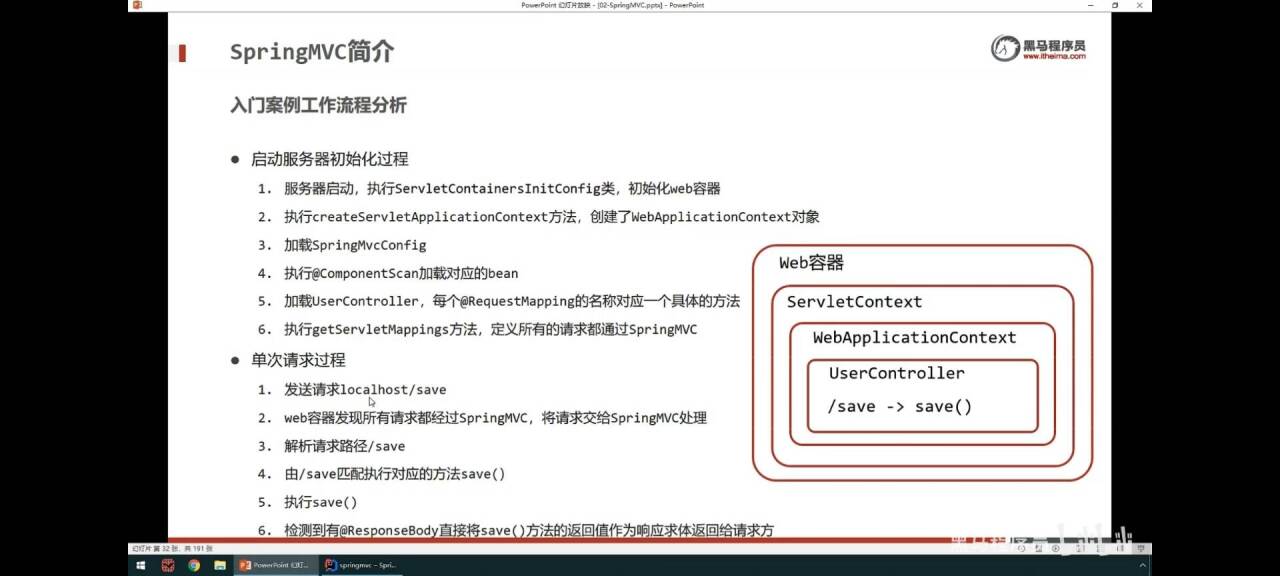
4.黑马学习笔记-SpringMVC(P43-P47)
1.SpringMVC简介 SpringMVC技术(更少的代码,简便)与servlet技术功能相同,属于web层开发技术。 SpringMVC是一种基于java实现MVC模型的轻量级web框架。 轻量级指的是(内存占用比较低,运行效率高)…...

【文件操作与IO】详细解析文件操作与IO (一)
本篇博客给大家带来的是文件操作的知识点. 🐎文章专栏: JavaEE初阶 🚀若有问题 评论区见 ❤ 欢迎大家点赞 评论 收藏 分享 如果你不知道分享给谁,那就分享给薯条. 你们的支持是我不断创作的动力 . 王子,公主请阅🚀 要开心要快乐顺便进步 一. …...

PMP考试费能报销吗?报销流程是什么?
最近也是到了6月和8月PMP考试的报名高峰期,后台有小伙伴最常问的问题就是,PMP考试费比较贵,能不能报销?报销流程是什么? 先给大家分享一下最新PMP报名消息和考试信息: 添加图片注释,不超过 140…...

机器学习05-CNN
CNN(卷积神经网络)学习文档 一、引言 卷积神经网络(Convolutional Neural Network,CNN)是深度学习中的一种重要网络结构,在图像识别、计算机视觉等领域取得了巨大成功。CNN 的设计灵感来源于生物视觉系统…...

c++ string构造函数和assign函数
c string构造函数和assign函数 #include <iostream> #include <stdlib.h> #include <string> #include <string.h>int main() {char buff[10] {a,b,c,d,e,f,g,h,i,\0};std::string str1;str1.assign(&buff[0],0,10);int length str1.length();i…...

学习threejs,使用EffectComposer后期处理组合器(采用RenderPass、GlitchPass渲染通道)
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:threejs gis工程师 文章目录 一、🍀前言1.1 ☘️THREE.EffectComposer 后期…...

物联网通信协议——TCP与MQTT的对比
在物联网通信中,MQTT和TCP的实现方式和原理完全不同,因为两者属于协议栈的不同层级,解决的问题也不同。以下从协议层级、工作机制和典型场景三个角度详细解释: 1. 协议层级与定位 特性TCPMQTT协议层级传输层(第4层&am…...
