【初阶数据结构】树——二叉树(上)
文章目录
目录
前言
一、树
1.树的概念与结构
2.树相关术语
3.树的表示
二、二叉树
1.概念与结构
2.特殊的二叉树
3.二叉树存储结构
总结
前言
本篇带大家学习一种非线性数据结构——树,简单认识树和二叉数以及了解二叉树的存储结构。
一、树
1.树的概念与结构

- 有⼀个特殊的结点,称为根结点,根结点没有前驱结点。
- 除根结点外,其余结点被分成 M(M>0) 个互不相交的集合 T1、T2、……、Tm ,其中每⼀个集合 Ti(1 <= i <= m) 又是⼀棵结构与树类似的⼦树。每棵⼦树的根结点有且只有⼀个前驱,可以有 0 个或多个后继。因此,树是递归定义的
注:树形结构中,子树之间不能有交集,否则就不是树形结构。
- 子树是不相交的(如果存在相交就是图了,图以后得课程会有讲解)
- 除了根结点外,每个结点有且仅有一个父结点
- 一棵N个结点的树有N-1条边
2.树相关术语
3.树的表示
struct TreeNode
{struct Node* child; // 左边开始的第⼀个孩⼦结点struct Node* brother; // 指向其右边的下⼀个兄弟结点int data; // 结点中的数据域
};

4.树形结构实际运用场景


二、二叉树
1.概念与结构

- 二叉树不存在度大于 2 的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树

2.特殊的二叉树

完全二叉树

二叉树性质根据满二叉树的特点可知:
- 若规定根结点的层数为 1 ,则一棵非空二叉树的第 i 层上最多有 2 i−1 个结点
- 若规定根结点的层数为 1 ,则深度为 h 的二叉树的最大结点数是 2 h − 1
- 若规定根结点的层数为 1 ,具有 n 个结点的满二叉树的深度 h = log2 (n + 1) ( log 以2为底, n+1 为对数)
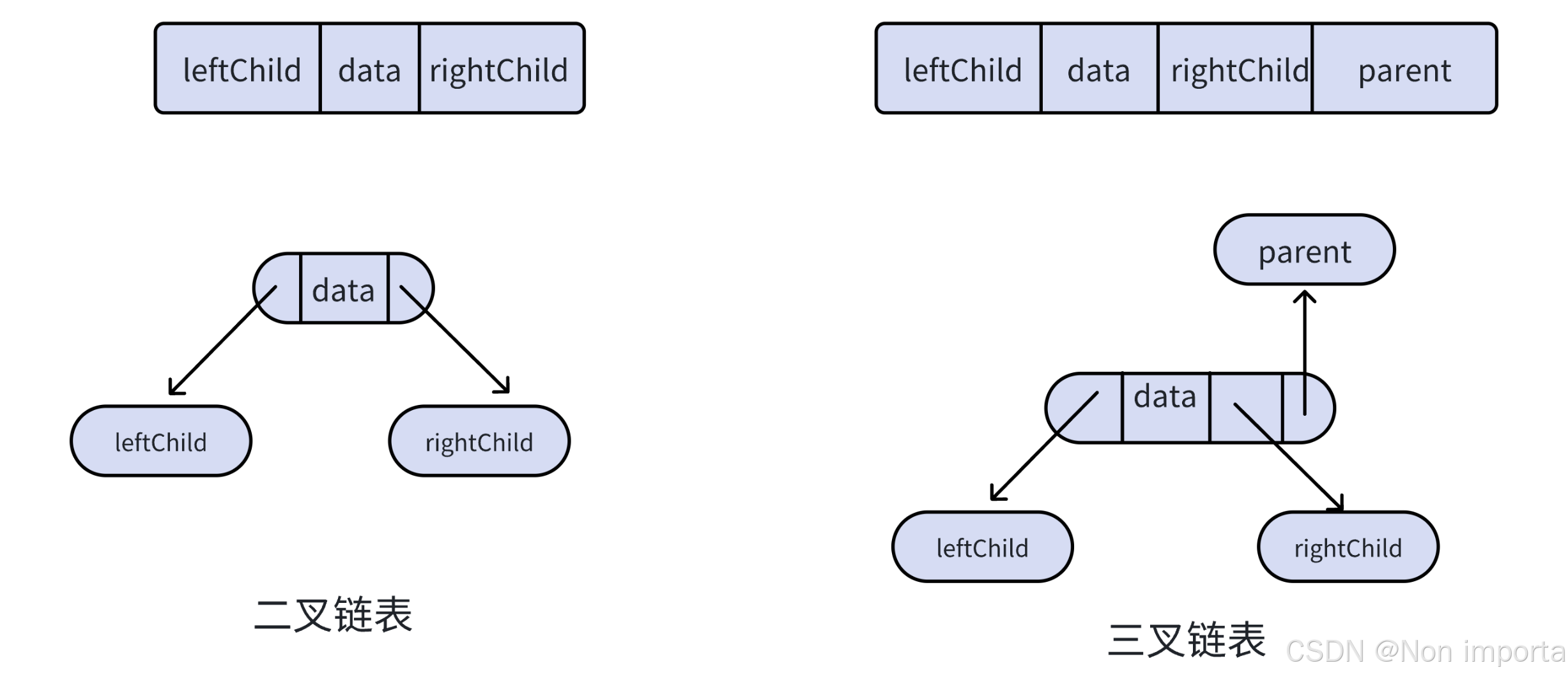
3.二叉树存储结构
顺序结构


链式结构

总结
非常感谢大家阅读完这篇博客。希望这篇文章能够为您带来一些有价值的信息和启示。如果您发现有问题或者有建议,欢迎在评论区留言,我们一起交流学习。
相关文章:

【初阶数据结构】树——二叉树(上)
文章目录 目录 前言 一、树 1.树的概念与结构 2.树相关术语 3.树的表示 二、二叉树 1.概念与结构 2.特殊的二叉树 3.二叉树存储结构 总结 前言 本篇带大家学习一种非线性数据结构——树,简单认识树和二叉数以及了解二叉树的存储结构。 一、树 1.树的概念与结构 树…...
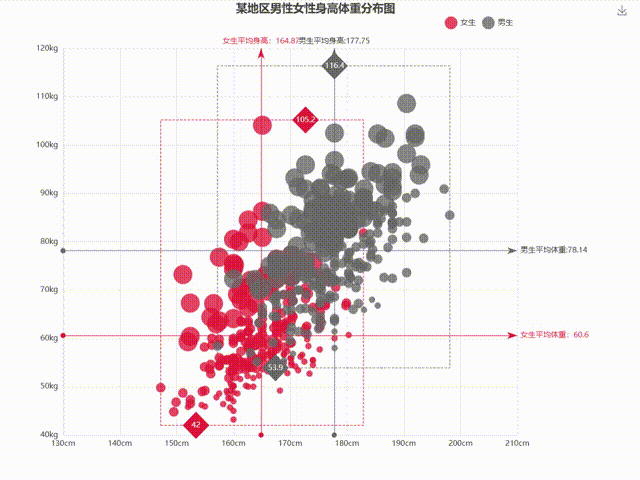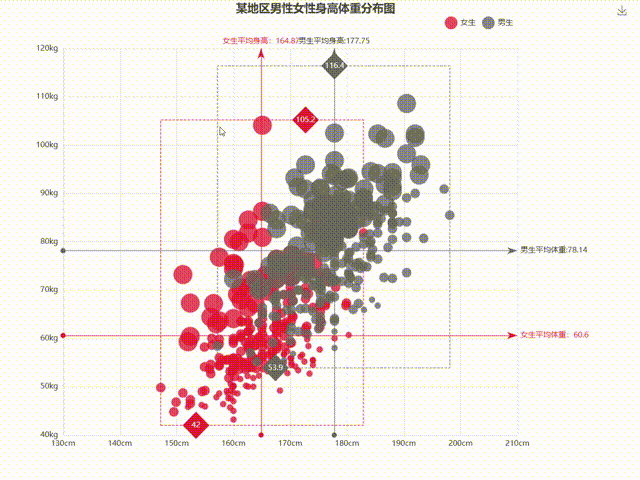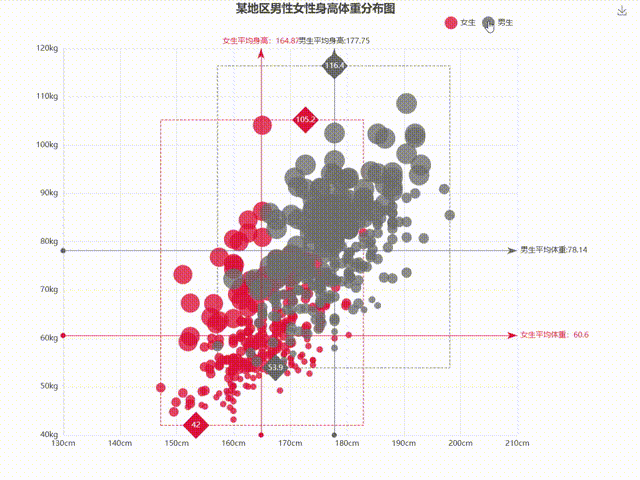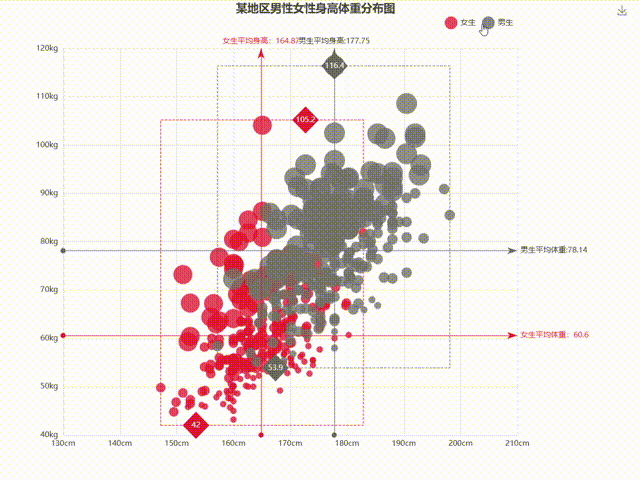
ECharts散点图-散点图14,附视频讲解与代码下载
引言: ECharts散点图是一种常见的数据可视化图表类型,它通过在二维坐标系或其它坐标系中绘制散乱的点来展示数据之间的关系。本文将详细介绍如何使用ECharts库实现一个散点图,包括图表效果预览、视频讲解及代码下载,让你轻松掌握…...

C++中的算术转换、其他隐式类型转换和显示转换详解
C中的类型转换(Type Conversion)是指将一个数据类型的值转换为另一个数据类型的过程,主要包括: 一、算术类型转换(Arithmetic Conversions) 算术类型转换通常发生在算术运算或比较中,称为**“标…...

GAIA-2:用于自动驾驶的可控多视图生成世界模型
25年3月来自英国创业公司 Wayze 的论文“GAIA-2: A Controllable Multi-View Generative World Model for Autonomous Driving”。(注:23年9月其发布GAIA-1) 生成模型为模拟复杂环境提供一种可扩展且灵活的范例,但目前的方法不足…...
CMake / MsBuild Ninja Make/ MSVC g++ clang++ 等c++编译概念解释)
(一)CMake / MsBuild Ninja Make/ MSVC g++ clang++ 等c++编译概念解释
c 几个编译概念 一 概念二 层级关系总结2.1层级表格2.2 关键点说明2.3 示例流程(以 Ninja 为例)2.4 示例流程(Windows 平台) 三 总结 一 概念 CMake 通过 CMakeLists.txt 生成不同平台的构建文件(如 .sln、build.n…...

创建 Node.js Playwright 项目:从零开始搭建自动化测试环境
一、环境准备 在开始创建 Playwright 项目之前,确保你的电脑上已经安装了以下工具: Node.js:Playwright 依赖于 Node.js 环境,确保你已经安装了最新版本的 Node.js。可以通过以下命令检查是否安装成功: node -v npm -…...

浅谈AI致幻
文章目录 当前形势下存在的AI幻觉(AI致幻)什么是AI幻觉AI幻觉的类型为什么AI会产生幻觉AI幻觉的危害与影响当前应对AI幻觉的技术与方法行业与学术界的最新进展未来挑战与展望结论 当前形势下存在的AI幻觉(AI致幻) 什么是AI幻觉 …...

postman乘法计算,变量赋值
postman脚本怎么计算乘法 在Postman中,你可以通过多种方式计算乘法,这取决于你的具体需求。例如,如果你想在发送请求前计算乘法结果,或者在测试标签中计算响应数据的乘法,下面是一些常见的方法。 1. 使用JavaScript代…...

自定义错误码的必要性
为什么要使用错误码,直接返回一个错误信息不好么? 下面介绍一下,在程序开发中使用错误码的必要性~ 便于排查问题 想象你开了一家奶茶店,顾客下单后可能出现各种问题: 没珍珠了(错误码:50…...

车载软件架构 --- 二级boot设计说明需求规范
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 周末洗了一个澡,换了一身衣服,出了门却不知道去哪儿,不知道去找谁,漫无目的走着,大概这就是成年人最深的孤独吧! 旧人不知我近况,新人不知我过…...

管理杂谈——采石矶大捷的传奇与启示
南宋抗金史上,岳飞与岳家军的铁血传奇家喻户晓,但另一位力挽狂澜的“文官战神”却常被忽视——他从未掌兵,却在南宋存亡之际整合溃军,以少胜多,缔造采石矶大捷。此人正是虞允文。一介书生何以扭转乾坤?他的…...

Java高效合并Excel报表实战:GcExcel让数据处理更简单
前言:为什么需要自动化合并Excel? 在日常办公场景中,Excel报表合并是数据分析的基础操作。根据2023年企业办公效率报告显示: 财务人员平均每周花费6.2小时在Excel合并操作上人工合并的错误率高达15%90%的中大型企业已采用自动化…...

第十四届蓝桥杯 2023 C/C++组 平方差
目录 题目: 题目描述: 题目链接: 思路: 核心思路: 第一种思路: 第二种思路: 坑点: 代码: 数学找规律 O(n) 50分代码详解: O(1)满分代码详解&#x…...

前端路由缓存实现
vue3缓存实现完整版,查看这篇设计和实现方式吧,更完整...

I/O复用函数的使用——select
I/O复用函数的使用——select 目录 一、概念 二、select接口 2.1 基础概念 2.2 使用 select 函数的标准输入读取代码 2.3 基于 select 模型的多客户端 TCP 服务器实现 一、概念 i/o复用使得程序能同时监听多个文件描述符,可以提高程序性能。 之前为了让服务器能…...

ubuntu20.04安装安装x11vnc服务基于gdm3或lightdm这两种主流的显示管理器。
前言:在服务端安装vnc服务,可以方便的远程操作服务器,而不用非要插上显示器才行。所以在服务器上安装vnc是很重要的。在ubuntu20中,默认的显示管理器已经变为gdm3,它可以带来与 GNOME 无缝衔接的体验,强调功…...

图像预处理-图像轮廓特征查找
其实就是外接轮廓,有了轮廓点就可以找到最上、最下、最左、最右的四个坐标(因为有xmin,xmax,ymin,ymax)。就可以绘制出矩形。 一.外接矩形 cv.boundingRect(轮廓点) - 返回x,y,w,h,传入一个轮廓的轮廓点,若有多个轮廓需…...

全同态加密医疗数据分析集python实现
目录 摘要一、前言二、全同态加密与医疗数据分析概述2.1 全同态加密(FHE)简介2.2 医疗数据分析需求三、数据生成与预处理四、系统架构与流程4.1 系统架构图五、核心数学公式六、异步任务调度与(可选)GPU 加速七、PyQt6 GUI 设计八、完整代码实现九、自查测试与总结十、展望…...

list的学习
list的介绍 list文档的介绍 list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过指针指向其前一个元素和后一…...

HarmonyOS:Navigation实现导航之页面设置和路由操作
导读 设置标题栏模式设置菜单栏设置工具栏路由操作页面跳转页面返回页面替换页面删除移动页面参数获取路由拦截 子页面页面显示类型页面生命周期页面监听和查询 页面转场关闭转场自定义转场共享元素转场 跨包动态路由系统路由表自定义路由表 示例代码 Navigation组件适用于模块…...

管道位移自动化监测方案
一、背景 管道系统在区域性地质沉降作用下易形成非均匀应力场集中现象,诱发管体屈曲变形及环焊缝界面剥离等连续损伤累积效应,进而导致管道力学性能退化与临界承载能力衰减。传统人工巡检受限于空间覆盖度不足及数据采集周期长(≥72h…...
和 plumberpdf 的对比分析及使用建议)
AI之pdf解析:Tesseract、PaddleOCR、RapidPaddle(可能为 RapidOCR)和 plumberpdf 的对比分析及使用建议
目录标题 Tesseract、PaddleOCR、RapidPaddle(可能为 RapidOCR)和 plumberpdf 的对比分析1. Tesseract类型: 开源 OCR 引擎特点:缺点:适用场景: 2. PaddleOCR (推荐)类型:特点:缺点:适用场景: 复杂版式文档、多语言混合文本、需要高精度识别的场景&#…...

【学习笔记】机器学习(Machine Learning) | 第五周| 分类与逻辑回归
机器学习(Machine Learning) 简要声明 基于吴恩达教授(Andrew Ng)课程视频 BiliBili课程资源 文章目录 机器学习(Machine Learning)简要声明 一、逻辑回归的基本原理分类判断条件模型输出的解释Sigmoid 函数与 Logistic 函数逻辑…...

悬停以及点击切换图片
为了实现悬停切换图片的功能,我们可以为每个按钮添加鼠标悬停事件监听器。以下是详细步骤和代码: 首先在控制器类中添加初始化方法,并添加事件监听器: package com.example.demo6;import javafx.event.ActionEvent; import java…...

Python 深度学习 第8章 计算机视觉中的深度学习 - 卷积神经网络使用实例
Python 深度学习 第8章 计算机视觉中的深度学习 - 卷积神经网络使用实例 内容概要 第8章深入探讨了计算机视觉中的深度学习,特别是卷积神经网络(convnets)的应用。本章详细介绍了卷积层和池化层的工作原理、数据增强技术、预训练模型的特征…...
之推导式)
Python基础总结(九)之推导式
文章目录 一、列表推导式1.1 列表推导式的格式1.2 列表推导式的注意事项1.3 列表推导式示例 二、 字典推导式2.1 字典推导式格式2.2 字典推导式注意事项2.3 字典推导式示例 三、 元组推导式3.1 元组推导式格式3.3 元组推导式示例 Python中的推导式有列表推导式,字典…...

[免费]SpringBoot+Vue博物馆(预约)管理系统【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的SpringBootVue博物馆(预约)管理系统,分享下哈。 项目视频演示 【免费】SpringBootVue博物馆(预约)管理系统 Java毕业设计_哔哩哔哩_bilibili 项目介绍 随着计算机科学技术的日渐成熟ÿ…...

基于LangChain4J的AI Services实践:用声明式接口重构LLM应用开发
基于LangChain4J的AI Services实践:用声明式接口重构LLM应用开发 前言:当Java开发遇上LLM编程困境 在LLM应用开发领域,Java开发者常面临两大痛点:一是需要手动编排Prompt工程、记忆管理和结果解析等底层组件,二是复杂…...

制作一款打飞机游戏12:初稿原型
当前进展 任务回顾:在之前,我们做了大量的规划和原型设计。我们创建了关卡,添加了侧向滚动和BOSS模式背景重复,还制作了一个紧凑的瓦片集。原型完成:我们完成了五个原型,基本实现了飞机飞行、滚动…...

【python】pyCharm常用快捷键使用-(2)
pyCharm常用快捷键使用 快速导入任意类 【CTRLALTSPACE】代码补全【CTRLSHIFTENTER】代码快速修正【ALTENTER】代码调试快捷键...
