线性代数 | 知识点整理 Ref 2
注:本文为 “线性代数 | 知识点整理” 相关文章合辑。
因 csdn 篇幅合并超限分篇连载,本篇为 Ref 2。
略作重排,未整理去重。
图片清晰度限于引文原状。
如有内容异常,请看原文。
【数学】线性代数知识点总结
阿巴 Jun 于 2024-11-11 16:58:05 发布
0. 前言
线性代数是数学的一个分支,线性代数的研究对象是向量、向量空间(又称线性空间),线性变换和有限维的线性方程组。即线性代数主要处理线性关系问题,线性关系即数学对象之间的关系是以一次形式来表达的。
线性(Linear)是指量与量之间按比例、成直线的关系,在数学上可以理解为一阶导数为常数的函数。
根据同济大学数学系编著的《线性代数》教材,将知识点按行列式、矩阵、向量组的线性相关性、相似矩阵及二次型、线性空间与线性变换五部分进行归纳总结。
1. 行列式
1.1 定义
矩阵的行列式,determinate(简称 det),是基于该矩阵的行列数据所计算的一个标量, n n n 阶行列式的几何意义是以 n n n 个向量为邻边的 n n n 维图形的体积。

注意:行列式的行数 = 列数,行列式引入求解线性方程组(后面将提到)。
1.2 性质
-
性质 1:行列互换,其值不变
即行列式与它的转置行列式的值相等, ∣ A ∣ = ∣ A T ∣ |A| = |A^T| ∣A∣=∣AT∣。
-
性质 2:行列式某行(列)的元素全为 0,行列式的值为 0。
几何上可以理解为该 n n n 阶行列式的值等于 n n n 维图形的体积,现在有一个维度(向量)长度为 0,则该图形这个维度上体积为 0。
放在定义式中,累加的每一项都是 0,因为累加的每一项是取自不同行不同列的 n n n 个元素乘积。
-
性质 3:行列式的某两行(列)元素相等或对应成比例,则行列式为零
几何上理解为组成 n n n 维图形的 n n n 个向量中,有两向量(边)在同一直线上,故在该图形这个维度上体积为 0。
在定义式中,成比例的项可以提出公因式,提出公因式后奇排列和偶排列的项会一一抵消(可以列一个简单的 3 阶行列式进行感受)。
-
性质 4:某行(列)所有的元素都是两个数的和,则可将其拆成两个行列式之和
如: ∣ a 1 + b 1 a 2 + b 2 a 3 + b 3 c 1 c 2 c 3 d 1 d 2 d 3 ∣ = ∣ a 1 a 2 a 3 c 1 c 2 c 3 d 1 d 2 d 3 ∣ + ∣ b 1 b 2 b 3 c 1 c 2 c 3 d 1 d 2 d 3 ∣ \left|\begin{array}{ccc} a_1 + b_1 & a_2 + b_2 & a_3 + b_3 \\ c_1 & c_2 & c_3 \\ d_1 & d_2 & d_3 \end{array}\right| = \left|\begin{array}{ccc} a_1 & a_2 & a_3 \\ c_1 & c_2 & c_3 \\ d_1 & d_2 & d_3 \end{array}\right| + \left|\begin{array}{ccc} b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ d_1 & d_2 & d_3 \end{array}\right| a1+b1c1d1a2+b2c2d2a3+b3c3d3 = a1c1d1a2c2d2a3c3d3 + b1c1d1b2c2d2b3c3d3
理解这件事情需要从定义式入手。

定义式是多项的累加,而每项都包含不同行列的元素之积,这里的可拆其实就是定义式中进行乘法分配律。
注意:行列式拆是只拆某行(列),而矩阵 A + B A + B A+B 相加指的是所有元素相加。
-
性质 5:两行(列)互换,行列式的值反号
反号是因为奇偶排列发生了改变,要理解这一点从定义中行列式的定义式入手, j 1 j 2 ⋯ j n j_1 j_2 \cdots j_n j1j2⋯jn 是排列,当为偶排列时带正号,为奇排列时带负号,行列式行(列)互换,奇偶排列改变,行列式的值反号。
-
性质 6:某行(列)元素有公因子 k k k( k ≠ 0 k \neq 0 k=0),则 k k k 可提到行列式外面
要理解性质 6 需要和性质 5 一样从行列式的定义式入手,某行(列)的元素都有公因子,代表定义式中累加的每一项都有公因子,那么相当于将每一项的这个公因子 k k k 提取到外面。
注意:行列式只是某行(列)公因子提到外面,而矩阵是每一个元素的公因子提到外面。
-
性质 7:某行(列)的 k k k 倍加到另一行(列),行列式的值不变
从定义式入手,结合定理 4,可以将其 “乘法分配律”,之后拆成原来的行列式与被加那行(列)替换为 k k k 倍加的那行的行列式相加,再根据性质 3 的理解,知道被加那行(列)替换为 k k k 倍加的那行的行列式为 0。
1.3 行列式展开定理(公式)
1.3.1 余子式与代数余子式
-
定义:在 n n n 阶行列式中,划去元素 a i j a_{ij} aij 所在的 i i i 行与 j j j 列的元,剩下的元不改变原来的顺序所构成的 n − 1 n - 1 n−1 阶行列式称为元素 a i j a_{ij} aij 的余子式。数学表示上记作 M i j M_{ij} Mij。
如: ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right| a11a21a31a12a22a32a13a23a33 中, a 22 a_{22} a22 的余子式 M 22 = ∣ a 11 a 13 a 31 a 33 ∣ M_{22} = \left|\begin{array}{cc} a_{11} & a_{13} \\ a_{31} & a_{33} \end{array}\right| M22= a11a31a13a33
-
而根据 M i j M_{ij} Mij 定义代数余子式 A i j = ( − 1 ) i + j M i j A_{ij} = (-1)^{i + j} M_{ij} Aij=(−1)i+jMij
则在上面行列式中 A 22 = ( − 1 ) 2 + 2 M 22 = ∣ a 11 a 13 a 31 a 33 ∣ A_{22} = (-1)^{2 + 2} M_{22} = \left|\begin{array}{cc} a_{11} & a_{13} \\ a_{31} & a_{33} \end{array}\right| A22=(−1)2+2M22= a11a31a13a33
-
引理:一个 n n n 阶行列式,如果其中第 i i i 行所有元素除 ( i , j ) (i, j) (i,j) 元 a i j a_{ij} aij 外都为零,那么这行列式等于 a i j a_{ij} aij 与它的代数余子式的乘积,即 D = a i j A i j D = a_{ij} A_{ij} D=aijAij
这一引理可以根据行列式的计算式推导(将 i i i 行和 j j j 列包含的含 0 项全部划掉,仅剩含 a i j a_{ij} aij 的项,提出 a i j a_{ij} aij 后剩下的为代数余子式)。
1.3.2 行列式按行(列)展开法则
-
定义:行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,即 D = a i 1 A i 1 + a i 2 A i 2 + ⋯ + a i n A i n D = a_{i1} A_{i1} + a_{i2} A_{i2} + \cdots + a_{in} A_{in} D=ai1Ai1+ai2Ai2+⋯+ainAin ( i = 1 , 2 , … , n ) (i = 1, 2, \ldots, n) (i=1,2,…,n) 或 D = a 1 j A 1 j + a 2 j A 2 j + ⋯ + a n j A n j D = a_{1j} A_{1j} + a_{2j} A_{2j} + \cdots + a_{nj} A_{nj} D=a1jA1j+a2jA2j+⋯+anjAnj ( j = 1 , 2 , … , n ) (j = 1, 2, \ldots, n) (j=1,2,…,n)。
这个法则可以根据引理与性质 4 或行列式计算式推导得到。
-
推论:行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零,即 a i 1 A j 1 + a i 2 A j 2 + ⋯ + a i n A j n = 0 a_{i1} A_{j1} + a_{i2} A_{j2} + \cdots + a_{in} A_{jn} = 0 ai1Aj1+ai2Aj2+⋯+ainAjn=0 ( i ≠ j ) (i \neq j) (i=j) 或 a 1 i A 1 j + a 2 i A 2 j + ⋯ + a n i A n j = 0 a_{1i} A_{1j} + a_{2i} A_{2j} + \cdots + a_{ni} A_{nj} = 0 a1iA1j+a2iA2j+⋯+aniAnj=0 ( i ≠ j ) (i \neq j) (i=j)。
推论的证明根据性质 3:行列式的某两行(列)元素相等或对应成比例,则行列式为零。
2. 矩阵
2.1 定义
-
由 m × n m \times n m×n 个数 a i j ( i = 1 , 2 , … , m ; j = 1 , 2 , … , n ) a_{ij} (i = 1, 2, \ldots, m; \ j = 1, 2, \ldots, n) aij(i=1,2,…,m; j=1,2,…,n) 排成的 m m m 行 n n n 列的数表 a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} a11a21⋮am1a12a22⋮am2⋯⋯⋯a1na2n⋮amn 称为 m m m 行 n n n 列矩阵,简称 m × n m \times n m×n 矩阵,记作 A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ) A = \left( \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) A= a11a21⋮am1a12a22⋮am2⋯⋯⋯a1na2n⋮amn 简记为 A = A m × n = ( a i j ) m × n = ( a i j ) A = A_{m \times n} = (a_{ij})_{m \times n} = (a_{ij}) A=Am×n=(aij)m×n=(aij)。
这 m × n m \times n m×n 个数称为矩阵 A A A 的元素,简称为元。元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。
- 行数和列数都等于 n n n 的矩阵称为 n n n 阶矩阵或 n n n 阶方阵。
2.1.1 矩阵与行列式概念区分

2.1.2 矩阵与线性变换
线性变换与矩阵之间存在着一一对应关系

由于矩阵和线性变换之间存在一一对应的关系,因此可以利用矩阵来研究线性变换,也可以利用线性变换来解释矩阵的含义。
2.2 矩阵的运算
2.2.1 矩阵的加法
-
定义:设由两个 m × n m \times n m×n 矩阵 A = ( a i j ) A = (a_{ij}) A=(aij) 和 B = ( b i j ) B = (b_{ij}) B=(bij),那么矩阵 A A A 与 B B B 的和记作 A + B A + B A+B,规定为 A + B = ( a 11 + b 11 a 12 + b 12 ⋯ a 1 n + b 1 n a 21 + b 21 a 22 + b 22 ⋯ a 2 n + b 2 n ⋮ ⋮ ⋮ a m 1 + b m 1 a m 2 + b m 2 ⋯ a m n + b m n ) A + B = \left( \begin{array}{cccc} a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1n} + b_{1n} \\ a_{21} + b_{21} & a_{22} + b_{22} & \cdots & a_{2n} + b_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} + b_{m1} & a_{m2} + b_{m2} & \cdots & a_{mn} + b_{mn} \end{array} \right) A+B= a11+b11a21+b21⋮am1+bm1a12+b12a22+b22⋮am2+bm2⋯⋯⋯a1n+b1na2n+b2n⋮amn+bmn 。
注意:只有两个矩阵 同型 时(行数等于行数、列数等于列数),这两个矩阵才能进行加法运算。
行列式加法是某行或某列加,矩阵是同型矩阵对应元素一一相加。
-
矩阵加法的运算规律
-
交换律: A + B = B + A A + B = B + A A+B=B+A
-
结合律: ( A + B ) + C = A + ( B + C ) (A + B) + C = A + (B + C) (A+B)+C=A+(B+C)
-
矩阵减法相当于: A − B = A + ( − B ) A - B = A + (-B) A−B=A+(−B)
其中 − B -B −B 称为 B B B 的负矩阵,有: B + ( − B ) = O B + (-B) = O B+(−B)=O
-
2.2.2 数与矩阵相乘
-
定义:数 λ \lambda λ 与矩阵 A A A 的乘积记作 λ A \lambda A λA 或 A λ A\lambda Aλ,规定为 λ A = A λ = ( λ a 11 λ a 12 ⋯ λ a 1 n λ a 21 λ a 22 ⋯ λ a 2 n ⋮ ⋮ ⋮ λ a m 1 λ a m 2 ⋯ λ a m n ) \lambda A = A\lambda = \left( \begin{array}{cccc} \lambda a_{11} & \lambda a_{12} & \cdots & \lambda a_{1n} \\ \lambda a_{21} & \lambda a_{22} & \cdots & \lambda a_{2n} \\ \vdots & \vdots & & \vdots \\ \lambda a_{m1} & \lambda a_{m2} & \cdots & \lambda a_{mn} \end{array} \right) λA=Aλ= λa11λa21⋮λam1λa12λa22⋮λam2⋯⋯⋯λa1nλa2n⋮λamn 。
行列式数乘是乘某行(列),矩阵数乘是乘每个元素。
-
矩阵数乘的运算规律
-
结合律: ( λ μ ) A = λ ( μ A ) (\lambda \mu) A = \lambda (\mu A) (λμ)A=λ(μA)
-
分配律: ( λ + μ ) A = λ A + μ A (\lambda + \mu) A = \lambda A + \mu A (λ+μ)A=λA+μA, λ ( A + B ) = λ A + λ B \lambda (A + B) = \lambda A + \lambda B λ(A+B)=λA+λB
-
2.2.3 矩阵与矩阵相乘
-
定义:设 A = ( a i j ) A = (a_{ij}) A=(aij) 是一个 m × s m \times s m×s 矩阵, B = ( b i j ) B = (b_{ij}) B=(bij) 是一个 s × n s \times n s×n 矩阵,那么规定矩阵 A A A 与矩阵 B B B 的乘积是一个 m × n m \times n m×n 矩阵 C = ( c i j ) C = (c_{ij}) C=(cij),其中 c i j = a i 1 b 1 j + a i 2 b 2 j + ⋯ + a i s b s j = ∑ k = 1 s a i k b k j c_{ij} = a_{i1} b_{1j} + a_{i2} b_{2j} + \cdots + a_{is} b_{sj} = \sum_{k=1}^{s} a_{ik} b_{kj} cij=ai1b1j+ai2b2j+⋯+aisbsj=∑k=1saikbkj ( i = 1 , 2 , … , m ; j = 1 , 2 , … , n ) (i = 1, 2, \ldots, m; \ j = 1, 2, \ldots, n) (i=1,2,…,m; j=1,2,…,n) 并把此乘积记作 C = A B C = AB C=AB。

显然,只有左矩阵的列数等于右矩阵的行数时,两个矩阵才能相乘。
-
矩阵乘法的运算规律
-
结合律: ( A B ) C = A ( B C ) (AB) C = A (BC) (AB)C=A(BC)
-
数乘的结合律: λ ( A B ) = ( λ A ) B = A ( λ B ) \lambda (AB) = (\lambda A) B = A (\lambda B) λ(AB)=(λA)B=A(λB)
-
分配律: A ( B + C ) = A B + A C A (B + C) = AB + AC A(B+C)=AB+AC, ( B + C ) A = B A + C A (B + C) A = BA + CA (B+C)A=BA+CA
-
单位矩阵再矩阵乘法中作用类似于数字 1: E m A m × n = A m × n E n = A E_m A_{m \times n} = A_{m \times n} E_n = A EmAm×n=Am×nEn=A
推论:矩阵乘法不一定满足交换律,但是纯量阵 λ E \lambda E λE 与任何同阶方阵都是可交换的,即: ( λ E n ) A n = λ A n = A n ( λ E n ) (\lambda E_n) A_n = \lambda A_n = A_n (\lambda E_n) (λEn)An=λAn=An(λEn)
-
2.2.4 矩阵的幂运算
-
定义:设 A A A 是 n n n 阶方阵,定义 A 1 = A A^1 = A A1=A, A 2 = A 1 A 1 A^2 = A^1 A^1 A2=A1A1,KaTeX parse error: Can't use function '\)' in math mode at position 6: \dots\̲)̲,A^{k + 1} = A^k A^1$,
其中 k k k 为正整数,显然只有方阵的幂才有意义。
-
矩阵的幂满足的运算规律
-
A k A l = A k + l A^k A^l = A^{k + l} AkAl=Ak+l
-
( A k ) l = A k l (A^k)^l = A^{kl} (Ak)l=Akl
-
2.2.5 矩阵的转置
-
定义:把矩阵 A A A 的行换成同序数的列得到的新矩阵,叫做 A A A 的 转置矩阵,记作 A T A^T AT。
注意:若 A = A T A = A^T A=AT,则将 A A A 称为 对称阵;若 A = − A T A = -A^T A=−AT,则将 A A A 称为 反对称阵。
-
转置矩阵的运算性质
-
( A T ) T = A (A^T)^T = A (AT)T=A
-
( A + B ) T = A T + B T (A + B)^T = A^T + B^T (A+B)T=AT+BT
-
( λ A ) T = λ A T (\lambda A)^T = \lambda A^T (λA)T=λAT
-
( A B ) T = B T A T (AB)^T = B^T A^T (AB)T=BTAT(穿脱原则)
-
2.2.6 方阵的行列式
-
定义:由 n n n 阶方阵 A A A 的元素所构成的行列式(各元素的位置不变),称为方阵 A A A 的行列式,记作 det A \det A detA 或 ∣ A ∣ |A| ∣A∣。
注意:方阵与行列式是两个不同概念, n n n 阶方阵是 n 2 n^2 n2 个数按一定方式排列成的 数表,而 n n n 阶行列式则是这个数表的数按一定的运算法则所确定的一个 数。
-
由 A A A 确定的 ∣ A ∣ |A| ∣A∣ 满足的运算规律
-
∣ A T ∣ = ∣ A ∣ |A^T| = |A| ∣AT∣=∣A∣(行列式性质 1)
-
∣ λ A ∣ = λ n ∣ A ∣ |\lambda A| = \lambda^n |A| ∣λA∣=λn∣A∣
-
∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB| = |A||B| ∣AB∣=∣A∣∣B∣
-
2.2.7 伴随矩阵
-
定义:行列式 ∣ A ∣ |A| ∣A∣ 的各个元素的代数余子式 ∣ A i j ∣ |A_{ij}| ∣Aij∣ 所构成的如下的矩阵 A ∗ = ( A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋯ ⋯ ⋯ ⋯ A 1 n A 2 n ⋯ A n n ) A^* = \left( \begin{array}{cccc} A_{11} & A_{21} & \cdots & A_{n1} \\ A_{12} & A_{22} & \cdots & A_{n2} \\ \cdots & \cdots & \cdots & \cdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \end{array} \right) A∗= A11A12⋯A1nA21A22⋯A2n⋯⋯⋯⋯An1An2⋯Ann 称为矩阵 A A A 的伴随矩阵。
-
伴随矩阵满足的性质:
A A ∗ = A ∗ A = ∣ A ∣ E AA^* = A^*A = |A|E AA∗=A∗A=∣A∣E
2.3 逆矩阵
2.3.1 定义
-
对于 n n n 阶矩阵 A A A,如果有一个 n n n 阶矩阵 B B B,使 A B = B A = E AB = BA = E AB=BA=E,则说矩阵 A A A 是可逆的,并把矩阵 B B B 称为 A A A 的逆矩阵,简称逆阵。
-
若矩阵 A A A 是可逆的,那么 A A A 的逆矩阵是唯一的。
-
A A A 的逆矩阵记作 A − 1 A^{-1} A−1,即若 A B = B A = E AB = BA = E AB=BA=E,则 B = A − 1 B = A^{-1} B=A−1。
2.3.2 相关定理
-
若矩阵 A A A 可逆,则 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0
-
若 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0,则矩阵 A A A 可逆,且 A − 1 = 1 ∣ A ∣ A ∗ A^{-1} = \frac{1}{|A|} A^* A−1=∣A∣1A∗
由定理 1 和 2 可知, A A A 是可逆矩阵的充分必要条件是 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0,即可逆矩阵就是非奇异矩阵。
推论:
-
若 A B = E AB = E AB=E(或 B A = E BA = E BA=E),则 B = A − 1 B = A^{-1} B=A−1
-
如果 A A A、 B B B 为同阶矩阵且均可逆,则 A − 1 A^{-1} A−1、 A T A^T AT、 λ A \lambda A λA ( λ ≠ 0 \lambda \neq 0 λ=0) 与 A B AB AB 也可逆,且
( A − 1 ) − 1 = A (A^{-1})^{-1} = A (A−1)−1=A
( A T ) − 1 = ( A − 1 ) T (A^T)^{-1} = (A^{-1})^T (AT)−1=(A−1)T
( λ A ) − 1 = 1 λ A − 1 (\lambda A)^{-1} = \frac{1}{\lambda} A^{-1} (λA)−1=λ1A−1
( A B ) − 1 = B − 1 A − 1 (AB)^{-1} = B^{-1} A^{-1} (AB)−1=B−1A−1
2.4 矩阵的初等变换与线性方程组
2.4.1 矩阵的初等变换
-
定义:下面三种变换称为矩阵的初等行变换:
-
对换两行(对换 i i i, j j j 两行,记作 r i ↔ r j r_i \leftrightarrow r_j ri↔rj);
-
以数 k ≠ 0 k \neq 0 k=0 乘某一行中的所有元(第 i i i 行乘 k k k,记作 r i × k r_i \times k ri×k);
-
把某一行所有元的 k k k 倍加到另一行对应的元上去(第 j j j 行的 k k k 倍加到第 i i i 行上,记作 r i + k r j r_i + k r_j ri+krj).
把定义中的 “行” 换成 “列”,即得矩阵的初等列变换的定义(所用记号是把 “ r r r” 换成 “ c c c”)
矩阵的初等行变换与初等列变换,统称初等变换。
-
-
显然,三种初等变换都是 可逆 的,且其逆变换是同一类型的初等变换:
-
r i ↔ r j r_i \leftrightarrow r_j ri↔rj 的逆变换是其本身
-
r i × k r_i \times k ri×k 的逆变换是 r i × ( 1 k ) r_i \times (\frac{1}{k}) ri×(k1)(或记作 r i ÷ k r_i \div k ri÷k)
-
r i + k r j r_i + k r_j ri+krj 的逆变换为 r i + ( − k ) r j r_i + (-k) r_j ri+(−k)rj(或记作 r i − k r j r_i - k r_j ri−krj)
-
2.4.2 矩阵之间的等价关系
如果矩阵 A A A 经有限次初等行变换变成矩阵 B B B,就称矩阵 A A A 与 B B B 行等价,记作 A ∼ r B A \stackrel{r}{\sim} B A∼rB;如果矩阵 A A A 经有限次初等列变换变成矩阵 B B B,就称矩阵 A A A 与 B B B 列等价,记作 A ∼ c B A \stackrel{c}{\sim} B A∼cB;如果矩阵 A A A 经有限次初等变换变成矩阵 B B B,就称矩阵 A A A 与 B B B 等价,记作 A ∼ B A \sim B A∼B。


-
矩阵之间的等价关系具有下列性质:
-
反身性: A ∼ A A \sim A A∼A;
-
对称性:若 A ∼ B A \sim B A∼B,则 B ∼ A B \sim A B∼A;
-
传递性:若 A ∼ B A \sim B A∼B, B ∼ C B \sim C B∼C,则 A ∼ C A \sim C A∼C。
-
我们可以通过初等变换来将矩阵变换为 “阶梯形”,便于计算:



这些矩阵相互之间的关系可以用下图表示:

2.5 初等变换与矩阵乘法的关系
2.5.1 初等矩阵
-
定义:由单位矩阵 E E E 经过一次初等变换得到的矩阵称为 初等矩阵。其中三种初等变换对应有三种初等矩阵
-
把单位矩阵中第 i i i, j j j 两行对换(或第 i i i, j j j 两列对换)
-
以数 k ≠ 0 k \neq 0 k=0 乘单位矩阵的第 i i i 行(或第 i i i 列)
-
以 k k k 乘单位矩阵的第 j j j 行加到第 i i i 行上或以 k k k 乘单位矩阵的第 i i i 列加到第 j j j 列上
-
-
定理:设 A A A 与 B B B 为 m × n m \times n m×n 矩阵,那么
-
A ∼ r B A \stackrel{r}{\sim} B A∼rB 的充分必要条件是存在 m m m 阶可逆矩阵 P P P,使 P A = B PA = B PA=B;
-
A ∼ c B A \stackrel{c}{\sim} B A∼cB 的充分必要条件是存在 n n n 阶可逆矩阵 Q Q Q,使 A Q = B AQ = B AQ=B;
-
A ∼ B A \sim B A∼B 的充分必要条件是存在 m m m 阶可逆矩阵 P P P 及 n n n 阶可逆矩阵 Q Q Q,使 P A Q = B PAQ = B PAQ=B。
-
以上定理可以用初等矩阵与矩阵 A A A 左乘与右乘证得,同时引出下面定义。
2.5.2 初等变换与矩阵乘法
-
性质:设 A A A 是一个 m × n m \times n m×n 矩阵,对 A A A 施行一次初等行变换,相当于在 A A A 的左边乘相应的 m m m 阶初等矩阵;对 A A A 施行一次初等列变换,相当于在 A A A 的右边乘相应的 n n n 阶初等矩阵。

2.6 矩阵的秩
2.6.1 秩
-
定义:设在矩阵 A A A 中有一个不等于 0 的 r r r 阶子式 D D D,且所有 r + 1 r + 1 r+1 阶子式(如果存在的话)全等于 0,那么 D D D 称为矩阵 A A A 的最高阶非零子式,数 r r r 称为矩阵 A A A 的秩,记作 R ( A ) R(A) R(A)。并规定零矩阵的秩等于 0
矩阵 A A A 的秩就是 A A A 中非零子式的最高阶数
-
关于矩阵的秩有以下结论:

-
一般的矩阵,当行数和列数较高时,按定义求秩是很麻烦的,一个自然的想法是用初等变换将一般的矩阵化为行阶梯形矩阵,行阶梯形矩阵的秩就等于非零行的行数,而两个等价的矩阵的秩相等。
-
矩阵的秩的性质:

2.6.2 结合秩判断线性方程组的解

3. 向量组的线性相关性
3.1 向量组及其线性组合
-
向量定义:
n n n 个有次序的数 a 1 , a 2 , ⋯ , a n a_1, a_2, \cdots, a_n a1,a2,⋯,an 所组成的数组称为 n n n 维向量,这 n n n 个数称为该向量的 n n n 个分量,第 i i i 个数 a i a_i ai 称为第 i i i 个分量。
-
分量全为实数的向量称为实向量
-
分量为复数的向量称为复向量
-
向量分为行向量和列向量
-
向量组定义:若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组。

-
定理:向量 b b b 能由向量组 A : a 1 , a 2 , ⋯ , a m A: a_1, a_2, \cdots, a_m A:a1,a2,⋯,am 线性表示的充分必要条件是矩阵 A = ( a 1 , a 2 , ⋯ , a m ) A = (a_1, a_2, \cdots, a_m) A=(a1,a2,⋯,am) 的秩等于矩阵 B = ( b 1 , b 2 , ⋯ , b m ) B = (b_1, b_2, \cdots, b_m) B=(b1,b2,⋯,bm) 的秩。


-
定理:向量组 B : b 1 , b 2 , ⋯ , b l B: b_1, b_2, \cdots, b_l B:b1,b2,⋯,bl 能由向量组 A : a 1 , a 2 , ⋯ , a m A: a_1, a_2, \cdots, a_m A:a1,a2,⋯,am 线性表示的充分必要条件是矩阵 A = ( a 1 , a 2 , ⋯ , a m ) A = (a_1, a_2, \cdots, a_m) A=(a1,a2,⋯,am) 的秩等于矩阵 ( A , B ) = ( a 1 , ⋯ , a m , b 1 , ⋯ , b l ) (A, B) = (a_1, \cdots, a_m, b_1, \cdots, b_l) (A,B)=(a1,⋯,am,b1,⋯,bl) 的秩,即 R ( A ) = R ( A , B ) R(A) = R(A, B) R(A)=R(A,B)
推论:向量组 A : a 1 , a 2 , ⋯ , a m A: a_1, a_2, \cdots, a_m A:a1,a2,⋯,am 与向量组 B : b 1 , b 2 , ⋯ , b l B: b_1, b_2, \cdots, b_l B:b1,b2,⋯,bl 等价的充分必要条件是 R ( A ) = R ( B ) = R ( A , B ) R(A) = R(B) = R(A, B) R(A)=R(B)=R(A,B)

3.2 向量组的线性相关性
-
定义:给定向量组 A : a 1 , a 2 , ⋯ , a m A: a_1, a_2, \cdots, a_m A:a1,a2,⋯,am,如果存在不全为零的数 k 1 , k 2 , ⋯ , k m k_1, k_2, \cdots, k_m k1,k2,⋯,km 使 k 1 a 1 + k 2 a 2 + ⋯ + k m a m = 0 k_1 a_1 + k_2 a_2 + \cdots + k_m a_m = 0 k1a1+k2a2+⋯+kmam=0,则称向量组 A A A 是线性相关的,否则称它线性无关。

-
线性相关与线性无关有其几何意义:

-
线性相关与线性无关的判断非常重要:


-
定理:

3.3 向量组的秩
-
定义:设有向量组 A A A,如果在 A A A 中能选出 r r r 个向量 a 1 , a 2 , ⋯ , a r a_1, a_2, \cdots, a_r a1,a2,⋯,ar 满足:
-
向量组 A 0 : a 1 , a 2 , ⋯ , a r A_0: a_1, a_2, \cdots, a_r A0:a1,a2,⋯,ar 线性无关;
-
向量组 A A A 中任意 r + 1 r + 1 r+1 个向量(如果 A A A 中有 r + 1 r + 1 r+1 个向量的话)都线性相关;
那么称向量组 A 0 A_0 A0 是向量组 A A A 的一个最大线性无关向量组,简称最大无关组。
最大无关组所含向量个数 r r r 称为向量组 A A A 的秩,记作 R A R_A RA。

-
3.4 线性方程组的解的结构

-
基础解系

-
解的关系

3.5 向量空间
3.5.1 向量空间定义
-
设 V V V 为 n n n 维向量的集合,如果集合 V V V 非空,且集合 V V V 对于向量的加法及数乘两种运算 封闭,那么就称集合 V V V 为向量空间。
-
所谓 封闭,是指在集合 V V V 中可以进行向量的加法以及数乘两种运算。具体地说,就是:若 a ∈ V a \in V a∈V, b ∈ V b \in V b∈V,则 a + b ∈ V a + b \in V a+b∈V;若 a ∈ V a \in V a∈V, λ ∈ R \lambda \in R λ∈R,则 λ a ∈ V \lambda a \in V λa∈V。
3.5.2 向量空间的基的概念

相对应的 坐标 概念:

4. 相似矩阵及二次型
4.1 向量的内积、长度及正交性
4.1.1 向量的内积

-
内积具有下列性质:
-
[ x , y ] = [ y , x ] [x, y] = [y, x] [x,y]=[y,x]
-
[ λ x , y ] = λ [ x , y ] [\lambda x, y] = \lambda [x, y] [λx,y]=λ[x,y]
-
[ x + y , z ] = [ x , z ] + [ y , z ] [x + y, z] = [x, z] + [y, z] [x+y,z]=[x,z]+[y,z]
-
当 x = 0 x = 0 x=0 时, [ x , x ] = 0 [x, x] = 0 [x,x]=0;当 x ≠ 0 x \neq 0 x=0 时, [ x , x ] > 0 [x, x] > 0 [x,x]>0
-
4.1.2 向量的长度

-
向量长度具有下列性质:
-
非负性:当 x ≠ 0 x \neq 0 x=0 时, ∣ ∣ x ∣ ∣ > 0 ||x|| > 0 ∣∣x∣∣>0;当 x = 0 x = 0 x=0 时, ∣ ∣ x ∣ ∣ = 0 ||x|| = 0 ∣∣x∣∣=0
-
齐次性: ∣ ∣ λ x ∣ ∣ = ∣ λ ∣ ∣ ∣ x ∣ ∣ ||\lambda x|| = |\lambda| ||x|| ∣∣λx∣∣=∣λ∣∣∣x∣∣
-
4.1.3 正交向量组
-
当 [ x , y ] = 0 [x, y] = 0 [x,y]=0 时,称向量 x x x 和向量 y y y 正交。

4.1.4 求规范正交基的方法
思路:基 $\Rightarrow) 正交基 $\Rightarrow) 规范正交基


4.1.5 正交矩阵及正交变换


4.2 方阵的特征值和特征向量

上面定义式可以进行以下推导:

特征值有以下相关结论:
设 n n n 阶矩阵 A = ( a i j ) A = (a_{ij}) A=(aij)

特征值与特征向量有以下定理:

4.3 相似矩阵


那么求相似变换矩阵 P P P,使 P − 1 A P = Λ P^{-1} AP = \Lambda P−1AP=Λ 为对角矩阵,这就称为把矩阵 A A A 对角化

4.4 对称矩阵的对角化


判断是否能够对角化:

对称矩阵对角化步骤:

4.5 二次型
4.5.1 二次型及其标准型


将二次型变成标准型:

4.5.2 矩阵合同

观察二次型的矩阵表示方式与合同的定义式,发现相同点。
4.5.3 化二次型为标准型


4.5.4 正定二次型



5. 线性空间与线性变换
5.1 线性空间的定义与性质


-
线性空间的性质:
-
零元素是唯一的,任意元素的负元素也是唯一的
-
如下等式成立: 0 ⋅ α = 0 0 \cdot \alpha = 0 0⋅α=0, ( − 1 ) ⋅ α = − α (-1) \cdot \alpha = -\alpha (−1)⋅α=−α


注意:一组向量要么线性相关要么线性无关,不存在第三种情况
-
5.2 维数、基与坐标


注意(基):

注意(坐标):

过渡矩阵:


5.3 坐标变换


5.4 线性变换
5.4.1 线性映射
-
概念:

线性映射概念:

相关性质:

5.4.2 线性映射的矩阵表示



5.4.2 线性变换的矩阵表示
线性变换概念:

线性变换的矩阵表示:



线性变换的运算:

线代知识点总结
dulu~dulu 已于 2024-12-17 11:39:53 修改
本节是线代某些知识点总结,可能较零碎。
对于简单的知识点,例如 “两行对应成比例,行列式为 0" 就不讲了。暂时不举例题,有时间会继续补充!
一 初等行 / 列变换
1. 计算行列式时,行列变换都可
因为 D = D T D = D^T D=DT,所以不论动行 / 列都是等价的。> 变换规则:>> 1.“倍乘”:行列式的某行 (列) 乘某个元素 k k k。相应的,若行列式中某行 (列) 元素有公因子 k k k ( k ≠ 0 k \neq 0 k=0),则 k k k 可提到行列式外面,即:>> ∣ k A ∣ = k n ∣ A ∣ |kA| = k^n |A| ∣kA∣=kn∣A∣ >> 2.“互换”:行列式中两行 (列) 互换,行列式变号。>> 3.“倍加”:某行 (列) 的 k k k 倍加到另一行 (列),行列式不变。
2. 求矩阵的秩时,行列变换都可
因为初等变换不改变某个矩阵非零子式的最高阶数,秩指的就是非零子式的最高阶数。> 初等变换的规则:>> 1.“倍乘”:一个非零常数乘矩阵矩阵的某一行 (列)。>> 2.“互换”:互换矩阵中某两行 (列) 的位置。>> 3.“倍加”:将矩阵的某一行 (列) 的 k k k 倍加到令一行 (列)。>>注意:>> 某矩阵乘元素 k k k,是矩阵中的每个元素都乘 k k k,要与行列式区分。>> 也就是 ∣ k A ∣ = k n ∣ A ∣ |kA| = k^n |A| ∣kA∣=kn∣A∣。
3. 解线性方程组时,仅能使用初等行变换
因为矩阵的每一种初等行变换都对应着线性方程组的同解变换,而作列变换会改变原来的方程。

4. 判定解的情况,单纯求 r ( A ) r(A) r(A), r ( A , b ) r(A, b) r(A,b) 的过程行列变换都可
注:将 r ( A , b ) r(A, b) r(A,b) 化行阶梯求秩时,往往我们需要 同时得到 r ( A ) r(A) r(A),如果想用列变换的话, 只能对 A A A 单独列变换,千万不要将 b b b 列和 A A A 的列混合运算,这样 r ( A ) r(A) r(A) 就不准了。(但 r ( A , b ) r(A, b) r(A,b) 是准的)。

但是,如果涉及到求通解或唯一解,那么就只能做行变换化行阶梯了,所以建议一开始就只做行变换。>总结:求解的过程,就只进行 初等行变换化行阶梯 求秩,并且顺势化为行最简型求解 。
5. 求向量组极大无关组、线性表出关系,则仅行变换**
因为初等行变换不改变列向量组的线性表出关系。例如下图, β \beta β 矩阵中, β 3 = β 2 + β 1 \beta_3 = \beta_2 + \beta_1 β3=β2+β1, α \alpha α 矩阵同样有这样的关系。

6. 求向量组的秩时,行列变换都可
求向量组的秩,其实最后会转化为求矩阵的秩,原理就是 “矩阵的秩 = 行向量组的秩 = 列向量组的秩”,所以求向量组的秩也是行列变换都可。

但是一般求向量组的秩后面会继续求解极大无关组 / 线性表出关系,这时只能做行变换,所以还是建议从开头就只使用行变换。
7. 求特征值时,行列变换都可
因为特征多项式本质上是行列式,求行列式时,行列都可以换。

8. 求特征向量时,仅做行变换
因为求特征向量时,本质是在解线性方程组,只能进行初等行变换。

9. 求逆矩阵时,对 ( A , E ) (A, E) (A,E) 仅做初等行变换
因为以 A − 1 A^{-1} A−1 左乘 A A A 得到 E E E,以 A − 1 A^{-1} A−1 左乘 E E E 得到 A − 1 A^{-1} A−1,以 A − 1 A^{-1} A−1 左乘的过程就是做初等行变换的过程。

所以怎么体现 A A A 和 E E E 做了完全一样的 A − 1 A^{-1} A−1 所带来的初等行变换,就是将 A A A, E E E 横着拼在一起,此时做的初等行变换就是同步的了。

总结:
除了① 求行列式的值(求特征值本质上就是求行列式的值)和 ② 单纯求秩,行列变换都可,其余情况通通只做行变换。
二 要牢记
先写那么多,后面有再补充:

一些推导:

对于 A B ≠ B A AB \neq BA AB=BA 的补充:

在 A B ≠ B A AB \neq BA AB=BA 的情况下,只能写成 ( A + B ) 2 = A 2 + A B + B A + B 2 (A + B)^2 = A^2 + AB + BA + B^2 (A+B)2=A2+AB+BA+B2

1. 矩阵的逆

推导如下:

初等矩阵的逆:

2. 矩阵的伴随

三 某某子式
1. 余子式
在 n n n 阶行列式中,去掉元素 a a a 所在的第 i i i 行、第 j j j 列元素,由剩下的元素按原来的位置与顺序组成的 n − 1 n - 1 n−1 阶行列式称为元素 a a a 的余子式,记作 M i j M_{ij} Mij。
2. 代数余子式
余子式 M i j M_{ij} Mij 乘 ( − 1 ) i + j (-1)^{i + j} (−1)i+j 后称为 a a a 的代数余子式,记作 A i j A_{ij} Aij

3. k k k 阶子式
给定一个矩阵,任取 k k k 行,任取 k k k 列,共 k 2 k^2 k2 个数构成的行列式,出现在矩阵的秩中,定义如下:
设 A A A 是 m × n m \times n m×n 矩阵,则若存在 k k k 阶子式不为零,而任意 k + 1 k + 1 k+1 阶子式(如果有的话)全为零,则 r ( A ) = k r(A) = k r(A)=k,且若 A A A 为 n × n n \times n n×n 矩阵,则:

4. k k k 阶主子式
指在行列式中选 k k k 行 k k k 列,但要求行和列的下标相同。如:行为 r 1 r_1 r1、 r 2 r_2 r2、 r 3 r_3 r3,列必须为 c 1 c_1 c1、 c 2 c_2 c2、 c 3 c_3 c3;行为 r 2 r_2 r2、 r 3 r_3 r3、 r 5 r_5 r5,列必须为 c 2 c_2 c2、 c 3 c_3 c3、 c 5 c_5 c5。因此, k k k 阶主子式不唯一。
这在矩阵相似会用到,下面会讲。
5. 顺序主子式
顺序主子式是在主子式上再加限定,顺序主子式是由 1~ k k k 行和 1~ k k k 列所确定的子式。>例如:>> 1 阶时:取第 1 行,第 1 列>> 2 阶时:取第 1、2 行,第 1、2 列>> 3 阶时:取第 1、2、3 行,第 1、2、3 列>> 4 阶时:取第 1、2、3、4 行,第 1、2、3、4 列>> 实际上,主子式的主对角线元素是原 n n n 阶行列式的主对角线元素的一部分,且顺序相同。>> 所以 k k k 阶主子式是不唯一的,而 k k k 阶顺序主子式是唯一的。
用在判断 二次型正定上,下面会讲。
四 矩阵的秩
① 0 ≤ r ( A ) ≤ min { m , n } 0 \leq r(A) \leq \min\{m, n\} 0≤r(A)≤min{m,n}
② r ( k A ) = r ( A ) r(kA) = r(A) r(kA)=r(A) ( k ≠ 0 k \neq 0 k=0)
③ r ( A B ) ≤ min { r ( A ) , r ( B ) } r(AB) \leq \min\{r(A), r(B)\} r(AB)≤min{r(A),r(B)}
④ r ( A + B ) ≤ r ( A ) + r ( B ) r(A + B) \leq r(A) + r(B) r(A+B)≤r(A)+r(B)
⑤

r ( A ) = n − 1 r(A) = n - 1 r(A)=n−1, r ( A ∗ ) = 1 r(A^*) = 1 r(A∗)=1 的证明:

进而可得出一个重要结论:> A m × n B n × s = 0 A_{m \times n} B_{n \times s} = 0 Am×nBn×s=0,则 r ( A ) + r ( B ) ≤ n r(A) + r(B) \leq n r(A)+r(B)≤n**
所以,看到 A × B A \times B A×B 就要想到两个结论:

⑥ 设 A A A 是 m × n m \times n m×n 矩阵, P P P, Q Q Q 分别是 m m m 阶, n n n 阶可逆矩阵,则> r ( A ) = r ( P A ) = r ( A Q ) = r ( P A Q ) r(A) = r(PA) = r(AQ) = r(PAQ) r(A)=r(PA)=r(AQ)=r(PAQ)
⑦ r ( A ) = r ( A T ) = r ( A A T ) = r ( A T A ) r(A) = r(A^T) = r(AA^T) = r(A^T A) r(A)=r(AT)=r(AAT)=r(ATA)
关于⑤的例题:

为什么 A x = b Ax = b Ax=b 有 n − r + 1 n - r + 1 n−r+1 个线性无关的解:

五 常用特征值与特征向量

针对 P − 1 A P = B P^{-1} AP = B P−1AP=B,如果知道 B B B 的特征值和特征向量,想要反求 A A A 的特征值特征向量,结论:
特征值不变,特征向量为 P ξ P\xi Pξ
证明过程:

注意这样一道例题:




关于特征值的一些提示:

六 矩阵,向量组,方程组
矩阵,向量组
① 向量组是由有限个相同维数的行向量或者列向量组成,其中向量是由 n n n 个实数组成的有序数组,是一个 n × 1 n \times 1 n×1 的矩阵 ( n n n 维列向量) 或是一个 1 × n 1 \times n 1×n 的矩阵 ( n n n 维行向量)。
② 矩阵是由 m × n m \times n m×n 个数排列成 m m m 行 n n n 列的数表。
一个向量组可以看作是一个矩阵的列(或行)向量集合。如果一个矩阵有 n n n 列,那么这 n n n 列就可以看作是一个由 n n n 个向量组成的向量组。反过来,一个矩阵也可以看作是由其列(或行)向量组成的向量组。
1. 怎么判断两个矩阵等价
矩阵等价的前提: A A A 与 B B B 是 ** 同型 **矩阵,即 A A A, B B B 行数,列数相同>> 矩阵等价的 充要条件:
① r ( A ) = r ( B ) r(A) = r(B) r(A)=r(B)
② P A Q = B PAQ = B PAQ=B, P P P, Q Q Q 可逆
2. 怎么判断两个向量组是等价向量组
向量组等价的前提: A A A, B B B 矩阵 ** 同维 **>> 若 r ( Ⅰ ) = r ( Ⅱ ) = r ( Ⅰ , Ⅱ ) r(\text{Ⅰ}) = r(\text{Ⅱ}) = r(\text{Ⅰ}, \text{Ⅱ}) r(Ⅰ)=r(Ⅱ)=r(Ⅰ,Ⅱ)>> 向量组等价的 充要条件:
① r ( Ⅰ ) = r ( Ⅱ ) r(\text{Ⅰ}) = r(\text{Ⅱ}) r(Ⅰ)=r(Ⅱ),且 (Ⅰ) 可由 (Ⅱ) 线性表出(单向表出即可)
② r ( Ⅱ ) = r ( Ⅰ ) r(\text{Ⅱ}) = r(\text{Ⅰ}) r(Ⅱ)=r(Ⅰ),且 (Ⅱ) 可由 (Ⅰ) 线性表出(单向表出即可)
③ r ( Ⅰ ) = r ( Ⅱ ) r(\text{Ⅰ}) = r(\text{Ⅱ}) r(Ⅰ)=r(Ⅱ),且 (Ⅰ) 可由 (Ⅱ) 线性表出(单向表出即可)
④ r ( Ⅰ ) = r ( Ⅱ ) = r ( Ⅰ , Ⅱ ) r(\text{Ⅰ}) = r(\text{Ⅱ}) = r(\text{Ⅰ}, \text{Ⅱ}) r(Ⅰ)=r(Ⅱ)=r(Ⅰ,Ⅱ),即>> r ( Ⅰ ) = r ( Ⅱ ) = r ( Ⅰ , Ⅱ ) r(\text{Ⅰ}) = r(\text{Ⅱ}) = r(\text{Ⅰ}, \text{Ⅱ}) r(Ⅰ)=r(Ⅱ)=r(Ⅰ,Ⅱ)
⑤ Ⅰ 和 Ⅱ 能够相互线性表示。

总结
① 两个矩阵 A A A 与 B B B 等价指的是 A A A 可以通过有限次初等变换变成 B B B。两个不同型矩阵是不可能等价的。
② 两个向量组等价只指的是它们能够互相线性表示,它们各自所含向量的个数可能是不一样的。
③ 两个向量组等价,一个线性无关,另一个不一定线性无关。

例题:

D. 即使 Ⅰ 和 Ⅱ 同为 n n n 维向量组,但是 s s s 与 t t t 的关系未知,也就是行数相等,列数未知,所以 A A A, B B B 两个矩阵可能不同型,不能等价。>> B. (Ⅰ) 可由(Ⅱ)表示,缺少其他条件,如果 ① 加上 (Ⅱ) 可由 (Ⅰ) 线性表出 或者 ② r ( Ⅰ ) = r ( Ⅱ ) r(\text{Ⅰ}) = r(\text{Ⅱ}) r(Ⅰ)=r(Ⅱ) 就对了>> C 正确>> D r ( A ) = r ( B ) r(A) = r(B) r(A)=r(B),只能推出两个向量组秩相同,缺少其他条件,如果加上 ① 加上 (Ⅱ) 可由 (Ⅰ) 线性表出 或者 ② 加上 (Ⅰ ) 可由 (Ⅱ) 线性表出或者③ r ( Ⅰ ) = r ( Ⅱ ) = r ( Ⅰ , Ⅱ ) r(\text{Ⅰ}) = r(\text{Ⅱ}) = r(\text{Ⅰ}, \text{Ⅱ}) r(Ⅰ)=r(Ⅱ)=r(Ⅰ,Ⅱ),就对了。

3. 矩阵和向量等价的比较

例题:

A. ( α 1 , α 2 , α 3 , 0 \alpha_1 ,\alpha_2, \alpha_3 ,0 α1,α2,α3,0) 能与 ( α 1 , α 2 , α 3 \alpha_1 ,\alpha_2, \alpha_3 α1,α2,α3) 相互线性表示,但是 ( α 1 , α 2 , α 3 , 0 \alpha_1 ,\alpha_2, \alpha_3 ,0 α1,α2,α3,0) 不是 A x = 0 Ax=0 Ax=0 的基础解系>> B. 基础解系一定是线性无关的,但是 B 选项 3 个向量是线性相关的(3 个向量相加 = 0)>> C. 像上面举的例子一样,$ α 1 α 2 , \alpha_1\alpha_2, α1α2,\beta_1 \beta_2$ 等秩,但是 α 1 α 2 \alpha_1\alpha_2 α1α2 与 β 1 β 2 \beta_1 \beta_2 β1β2 不能相互线性表示。
D.
在 ( α 1 , α 2 , α 3 \alpha_1 ,\alpha_2, \alpha_3 α1,α2,α3) 的右边乘可逆矩阵,不改变原来矩阵的秩,且 ( β 1 , β 2 , β 3 \beta_1 ,\beta_2, \beta_3 β1,β2,β3 ) 与 ( α 1 , α 2 , α 3 \alpha_1 ,\alpha_2, \alpha_3 α1,α2,α3) 能相互线性表示>>所以,求 A x = 0 Ax=0 Ax=0 的另一个基础解析,需要满足与 ( α 1 , α 2 , α 3 \alpha_1 ,\alpha_2, \alpha_3 α1,α2,α3) 等价且等秩。

4. 同解方程组
若两个方程组 A m × n x = 0 A_{m \times n} x = 0 Am×nx=0 与 B s × n x = 0 B_{s \times n} x = 0 Bs×nx=0 有完全相同的解,则称它们为同解方程组
充要条件:
① A x = 0 Ax=0 Ax=0 的解满足 B x = 0 Bx=0 Bx=0,且 B x = 0 Bx=0 Bx=0 的解满足 A x = 0 Ax=0 Ax=0(互相把解代入求出结果即可)
② r ( A ) = r ( B ) r(A) = r(B) r(A)=r(B),且 A x = 0 Ax=0 Ax=0 的解满足 B x = 0 Bx=0 Bx=0(或 B x = 0 Bx=0 Bx=0 的解满足 A x = 0 Ax=0 Ax=0)
③ r ( A ) = r ( B ) = r ( [ A B ] ) r(A) = r(B) = r \left( \begin{bmatrix} A \\ B \end{bmatrix} \right) r(A)=r(B)=r([AB])(三秩相同)

如果是齐次线性方程组,那么 A A A, B B B 是同解方程组,若是非齐次那么就不对了。
例 1:

例 2:

例 3:

七 齐次线性方程组和非齐次线性方程组
齐次线性方程组有解的条件:
① r ( A ) = n r(A) = n r(A)=n 时,方程组有 唯一零解。
② r ( A ) = r < n r(A) = r < n r(A)=r<n 时,方程组有非零解(无穷多解),且有 n − r n - r n−r 个线性无关解>>齐次方程组其实就是解和系数的正交,例如,给你一个条件:
α 1 = 2 α 2 + α 3 \alpha_{1} = 2\alpha_{2} + \alpha_{3} α1=2α2+α3----> α 1 − 2 α 2 − α 3 + 0 α 4 = 0 \alpha_{1} - 2\alpha_{2} - \alpha_{3} + 0 \alpha_{4} = 0 α1−2α2−α3+0α4=0

则 ( 1 , − 2 , − 1 , 0 ) (1, -2, -1, 0) (1,−2,−1,0) 就是齐次方程组的基础解系
非齐次线性无关组有解的条件:
① 若 r ( 4 ) ≠ r ( [ A , b ] ) r(4) \neq r([A, b]) r(4)=r([A,b]),则方程组无解;
② 若 r ( A ) = r ( [ A , b ] ) = n r(A) = r([A, b]) = n r(A)=r([A,b])=n,则方程组有唯一解;
③ r ( A ) = r ( [ A , b ] ) = r < n r(A) = r([A, b]) = r < n r(A)=r([A,b])=r<n,则方程组有无穷多解。
非齐次方程组的通解的求法:
① 求 A x = 0 Ax = 0 Ax=0 的解
② 求 A x = b Ax = b Ax=b 的一个特解
③ 非齐次方程组的通解 = 齐次方程组的解 + 一个非齐次的特解

如果 A A A 行满秩,则 r ( A ) = r ( A ∣ b ) r(A) = r(A|b) r(A)=r(A∣b),那么方程组一定有解。
如果 A A A 列满秩,则 r ( A ) r(A) r(A) 与 r ( A ∣ b ) r(A|b) r(A∣b) 的关系不确定:
① r ( A ) < r ( A ∣ b ) r(A) < r(A|b) r(A)<r(A∣b),则无解
② r ( A ) = r ( A ∣ b ) < n r(A) = r(A|b) < n r(A)=r(A∣b)<n,有无穷多解
③ r ( A ) = r ( A ∣ b ) = n r(A) = r(A|b) = n r(A)=r(A∣b)=n,有唯一解
非齐次方程组解的性质:> 若 η 1 , η 2 , η 3 \eta_1, \eta_2, \eta_3 η1,η2,η3 是非齐次线性方程组 A x = b Ax = b Ax=b 的解, ξ \xi ξ 是对应齐次方程组 A x = 0 Ax = 0 Ax=0 的解,则:
(1) η 1 − η 2 \eta_1 - \eta_2 η1−η2 是 A x = 0 Ax = 0 Ax=0 的解;
(2) k ξ + η k\xi + \eta kξ+η 是 A x = b Ax = b Ax=b 的解
扩展:

解释:
- p p p 个解的任意组合,都是齐次线性方程组的解
- 非齐次的解线性组合也能得到齐次线性方程组的解,但是需要满足 k 1 + k 2 + ⋯ + k p = 0 k_1 + k_2 + \cdots + k_p = 0 k1+k2+⋯+kp=0,例如, α 1 − α 2 \alpha_1 - \alpha_2 α1−α2(1 - 1 = 0), α 1 − α 2 \alpha_1 - \alpha_2 α1−α2 就是齐次线性方程组的解。
- 非齐次的解线性组合也能得到非齐次线性方程组的解,但是需要满足 k 1 + k 2 + ⋯ + k p = 1 k_1 + k_2 + \cdots + k_p = 1 k1+k2+⋯+kp=1,例如, ( α 1 + α 2 ) / 2 (\alpha_1 + \alpha_2)/2 (α1+α2)/2,就是非齐次线性方程组的一个解。
- 齐次线性方程组的解与非齐次线性方程组的解相加,得到的是非齐次线性方程组的解。
- r ( A ) = r r(A) = r r(A)=r, A A A 就有 n − r n - r n−r 个线性无关的解,而 x 1 , x 2 , … , x n − r x_1, x_2, \ldots, x_{n - r} x1,x2,…,xn−r 刚好是 A x = 0 Ax = 0 Ax=0 的 n − r n - r n−r 个线性无关解,所以>> k 1 x 1 + k 2 x 2 + ⋯ + k n − r x n − r k_1 x_1 + k_2 x_2 + \cdots + k_{n - r} x_{n - r} k1x1+k2x2+⋯+kn−rxn−r 是 A x = 0 Ax = 0 Ax=0 的解。
例题:

A. α 1 − α 2 \alpha_1 - \alpha_2 α1−α2 是组合系数是 1 - 1 = 0, α 1 − α 2 \alpha_1 - \alpha_2 α1−α2 是 A x = 0 Ax = 0 Ax=0 的解
B. 3 α 1 − 2 α 2 3\alpha_1 - 2\alpha_2 3α1−2α2 是 A x = b Ax = b Ax=b 的解,C, D 同理。
八 对比记忆
1.
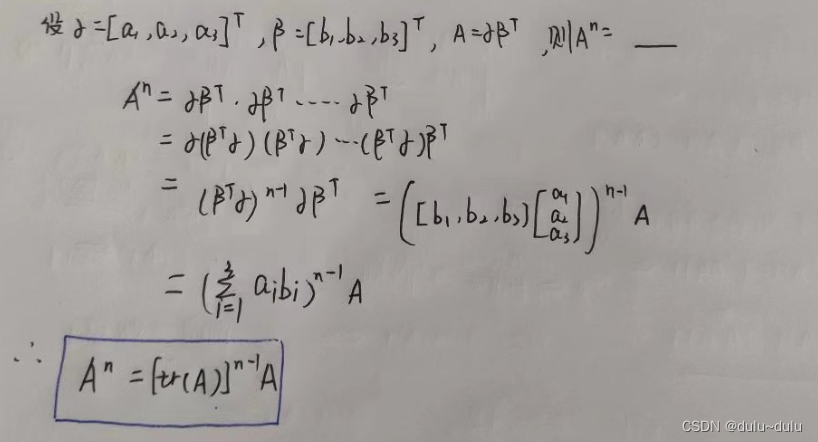
矩阵 A A A 的 tr ( A ) \text{tr}(A) tr(A): tra ( A ) = \text{tra}(A) = tra(A)= 矩阵 A A A 的迹 = = = 对角线元素之和
2. 对于秩为 1 的 n n n 阶矩阵 A A A 或 A = α β T A = \alpha \beta^T A=αβT(或 β T α \beta^T \alpha βTα)( α \alpha α, β \beta β 都是 n n n 维非零列向量),其特征值为 λ 1 = λ 2 = λ 3 = ⋯ = λ n − 1 = 0 \lambda_1 = \lambda_2 = \lambda_3 = \cdots = \lambda_{n - 1} = 0 λ1=λ2=λ3=⋯=λn−1=0, λ n = ∑ i = 1 n a i i = β T α \lambda_n = \sum_{i = 1}^{n} a_{ii} = \beta^T \alpha λn=∑i=1naii=βTα(或 α T β \alpha^T \beta αTβ)

3.

例题 1:

例题 2:

九 相似与正交
存在 n n n 阶可逆矩阵 P P P,使得 P − 1 A P = B P^{-1} AP = B P−1AP=B,则称 A A A 相似于 B B B,记为 A ∼ B A \sim B A∼B
若 A ∼ B A \sim B A∼B
① ∣ A ∣ = ∣ B ∣ |A| = |B| ∣A∣=∣B∣
② r ( A ) = r ( B ) r(A) = r(B) r(A)=r(B)
③ tr ( A ) = tr ( B ) \text{tr}(A) = \text{tr}(B) tr(A)=tr(B)
④ λ A = λ B \lambda_A = \lambda_B λA=λB( ∣ λ E − A ∣ = ∣ λ E − B ∣ |\lambda E - A| = |\lambda E - B| ∣λE−A∣=∣λE−B∣)
⑤ r ( λ E − A ) = r ( λ E − B ) r(\lambda E - A) = r(\lambda E - B) r(λE−A)=r(λE−B)
⑥ A A A, B B B 各阶主子式之和分别相同
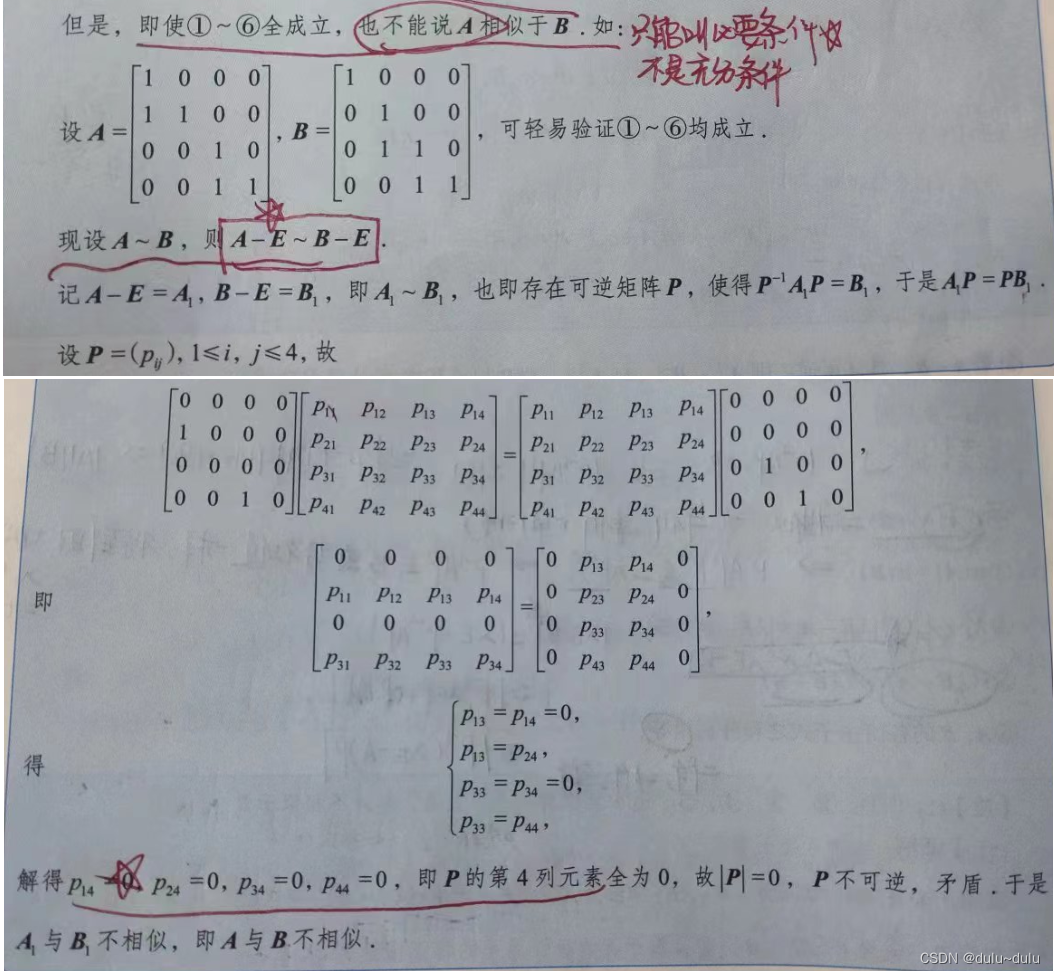
也就是说, A A A 与 B B B 即使特征值相同,但也不一定相似。但是如果 A A A, B B B 都是实对称矩阵,那么相似,则一定特征值相同(实对称矩阵一定能相似对角化,特征值相同一定能相似于同一个对角矩阵,根据传递性 A ∼ B A \sim B A∼B)。
如何判定矩阵相似
① 定义法
存在 n n n 阶可逆矩阵 P P P,使得 P − 1 A P = B P^{-1} AP = B P−1AP=B
② 传递法
A ∼ Λ A \sim \Lambda A∼Λ, Λ ∼ B \Lambda \sim B Λ∼B,则 A ∼ B A \sim B A∼B,其中 Λ \Lambda Λ 为对角阵
这就要说到矩阵的相似对角化
矩阵可相似对角化的条件:
充要条件:
① n n n 阶矩阵 A A A 可相似对角化 ⇔ \Leftrightarrow ⇔ 有 n n n 个线性无关的特征向量。
② n n n 阶矩阵 A A A 可相似对角化 ⇔ \Leftrightarrow ⇔ A A A 对应于每个 k k k 重特征值都有 k k k 个线性无关的特征向量
必要条件:
③ n n n 阶矩阵 A A A 有 n n n 个不同特征值 ⇒ \Rightarrow ⇒ A A A 可相似对角化
④ n n n 阶矩阵为 实对称矩阵 ⇒ \Rightarrow ⇒ A A A 可相似对角化
对于矩阵相似对角化的步骤:
① 求特征值
② 求特征向量
③ 正交化(如果需要的话),单位化 η 1 , η 2 , η 3 , … , η n \eta_1, \eta_2, \eta_3, \ldots, \eta_n η1,η2,η3,…,ηn
④ 令 Q = [ η 1 , η 2 , η 3 , … , η n ] Q = [\eta_1, \eta_2, \eta_3, \ldots, \eta_n] Q=[η1,η2,η3,…,ηn],则 Q Q Q 为正交矩阵,且 Q − 1 A Q = Q T A Q = Λ Q^{-1} AQ = Q^T AQ = \Lambda Q−1AQ=QTAQ=Λ
上面提到了实对称矩阵,实对称矩阵就是组成 A A A 的元素都是实数。对于实对称矩阵( A T = A A^T = A AT=A)要记住:

对于正交,需要记住:
① α T β = 0 \alpha^T \beta = 0 αTβ=0,则 α \alpha α, β \beta β 是正交向量
② 若满足 A T A = E A^T A = E ATA=E,则 A A A 是正交矩阵
A T A = E ⇔ A − 1 = A T A^T A = E \Leftrightarrow A^{-1} = A^T ATA=E⇔A−1=AT
③ 若 A A A 为正交矩阵,则 A T A^T AT 为正交矩阵, A − 1 A^{-1} A−1 为正交矩阵, A ∗ A^* A∗ 为正交矩阵, − A -A −A 为正交矩阵
④ 若 A A A, B B B 为同阶正交矩阵,则 A B AB AB 为正交矩阵, A + B A + B A+B 不一定为正交矩阵
⑤ 若 A A A 为正交矩阵,则其特征值的取值范围为 { − 1 , 1 } \{-1, 1\} {−1,1}

在易错知识点有补充。
例题:

不可对角化的矩阵怎么判断相似:
例题:

如果 A A A 与 B B B 相似,那么:
对于任意实数 k k k 和整数 n n n,有 ( A + k E ) n (A + kE)^n (A+kE)n 与 ( B + k E ) n (B + kE)^n (B+kE)n 相似
对于上面这道题,取 k = − 1 k = -1 k=−1, n = 1 n = 1 n=1,判断哪两个矩阵相似。
矩阵相似还可得出:
① A ∼ B A \sim B A∼B, A k = B k A^k = B^k Ak=Bk, f ( A ) = f ( B ) f(A) = f(B) f(A)=f(B)
② 若 A ∼ B A \sim B A∼B,且 A A A 可逆,则 A − 1 ∼ B − 1 A^{-1} \sim B^{-1} A−1∼B−1, f ( A − 1 ) = f ( B − 1 ) f(A^{-1}) = f(B^{-1}) f(A−1)=f(B−1)
③ 若 A ∼ B A \sim B A∼B, A ∗ ∼ B ∗ A^* \sim B^* A∗∼B∗
④ 若 A ∼ B A \sim B A∼B, A T ∼ B T A^T \sim B^T AT∼BT

注:
提醒:

再次提醒,矩阵等价怎么判定:
设 A A A, B B B 均为 m × n m \times n m×n 矩阵,若存在可逆矩阵 P m × n P_{m \times n} Pm×n, Q m × n Q_{m \times n} Qm×n,使得 P A Q = B PAQ = B PAQ=B,则 A A A, B B B 是等价矩阵。若 A A A, B B B 是同型矩阵,则 A A A 与 B B B 等价的充分必要条件是 r ( A ) = r ( B ) r(A) = r(B) r(A)=r(B)
十 实对称矩阵
实对称矩阵中不同特征值对应的特征向量相互正交。

实对称矩阵可以用正交矩阵相似对角化,这是必然的。

要与合同区别,合同:对于实对称矩阵 A A A,必存在可逆矩阵 C C C,使得 C T A C = λ C^T A C = \lambda CTAC=λ, λ \lambda λ 对角矩阵,这里的 C C C 不是 A A A 的特征向量, λ \lambda λ 也不是 A A A 的特征值。
若普通矩阵能相似对角化,能不能用正交矩阵相似对角化?
对于 n n n 阶实对称矩阵, n n n 个线性无关的特征向量即使不正交,也可以通过施密特正交实现正交化,再单位化得到正交矩阵。那普通矩阵可以相似对角化,他也有 n n n 个线性无关的特征向量,其特征向量是否可以正交化,单位化,再用得到的正交矩阵 Q Q Q 进行相似对角化?
答案是否定的。

1. A A A 为 n n n 阶实对称矩阵的充分必要条件为: A A A 有 n n n 个正交的特征向量。

为什么不能是普通矩阵
例题:

2. A A A 为实对称矩阵的则 A ∗ A^* A∗ 为实对称矩阵,反过来不对。

十一 合同
设 A A A, B B B 为 n n n 阶矩阵,若存在可逆矩阵 C C C,使得 C T A C = B C^T A C = B CTAC=B,则称 A A A 与 B B B 合同,即 A ≅ B A \cong B A≅B。 A A A 与 B B B 合同,就是指同一个 二次型 在 可逆线性变换 下的两个不同状态的联系。



注:由于我们已经规定,对称矩阵才是二次型矩阵,所以二次型矩阵都是对称矩阵,相应的和对称矩阵合同的矩阵也是对称矩阵。
例题:




十二 二次型
关于二次型化标准型或规范型的方法:配方法,正交变化有总结如下:

所以我们可以进一步得到
等价,合同和相似的关系:

注:相似一定合同的前提条件是 A A A, B B B 都是实对称矩阵

例题:




关于配方法和正交变换分别给一个例题:
配方法:

正交变换:


① 若 λ 1 = λ 2 \lambda_1 = \lambda_2 λ1=λ2,那么两个同一特征值对应的特征向量需要正交化,如果本来就正交可以不做这一步,所以在计算特征值的时候,可以将两个特征向量写为正交的,这样就免去了施密特正交化,直接进入单位化即可。
② λ 1 ≠ λ 2 ≠ λ 3 \lambda_1 \neq \lambda_2 \neq \lambda_3 λ1=λ2=λ3,那么不用进行施密特正交,直接单位化即可。
常见题型:
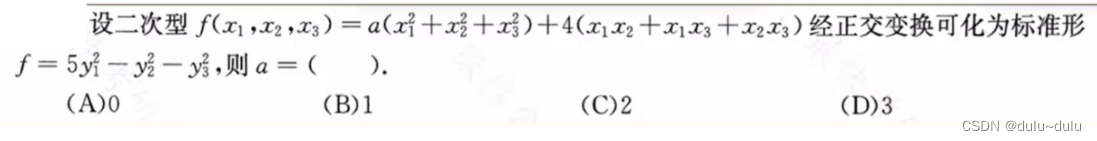

这里记录一个例题:


若二次型中只有混合项,没有平方项,要怎么做?

两类典型大题:【线代救命 #6】一个视频彻底搞懂二次型 !!_哔哩哔哩_bilibili
如果两个矩阵相似,那么可以直接用标准型作为桥梁,无需化为规范型:

如果两个矩阵不相似,那么只能用规范型作为桥梁,因为两个矩阵合同,规范型是唯一的:

十三 二次型正定
二次型正定的充要条件:
n n n 元二次型 f = x T A x f = x^T A x f=xTAx 正定 ⇔ \Leftrightarrow ⇔ 对任意 x ≠ 0 x \neq 0 x=0,有 x T A x > 0 x^T A x > 0 xTAx>0(定义)
① ⇔ \Leftrightarrow ⇔ f f f 的正惯性指数 p = n p = n p=n
② ⇔ \Leftrightarrow ⇔ 存在可逆矩阵 D D D,使得 A = D T D A = D^T D A=DTD
③ ⇔ \Leftrightarrow ⇔ A ≅ E A \cong E A≅E, A A A 与 E E E 合同
② ③ 推导:

④ ⇔ \Leftrightarrow ⇔ A A A 的特征值 λ > 0 \lambda > 0 λ>0
⑤ ⇔ \Leftrightarrow ⇔ A A A 的全部顺序主子式 > 0
二次型正定的必要条件:
① a i i > 0 a_{ii} > 0 aii>0,对角线元素全部大于 0
② ∣ A ∣ > 0 |A| > 0 ∣A∣>0
最好是使用充要条件 ① ④ ⑤ 判断二次型是否正定,如果非要用定义法,来看个例题:

注意上题,不能直接将 f f f 判定为正定:
因为将二次型化为标准型的过程一定要做可逆线性变换

例题 1:


例题 2:




看到这种平方和形式的二次型,要想到他一些性质:
平方和形式的二次型(重要):


例题:

答案 C,由于二次型矩阵正定,则 r ( B ) r(B) r(B) 满秩,进而推出 ∣ B ∣ ≠ 0 |B| \neq 0 ∣B∣=0

注意一定要是平方和,下面这个就不是,就只能用开头讲的特征值法,配方法和合同变换:

关于正定的重要结论:


十四 秩 1 矩阵的性质(重要)
假设 A A A 是一个秩为 1 的矩阵, α \alpha α 与 β \beta β 为列向量,且 α β T = β α T = A \alpha \beta^T = \beta \alpha^T = A αβT=βαT=A
1. 如果一个矩阵能由一个列向量 × \times × 一个行向量表示,那么这个矩阵秩一定为 1,即 r = 1 r = 1 r=1。同样,一个秩为 1 的矩阵,可以拆成一个列向量 × \times × 一个行向量,并且表示方法不唯一。

2. 矩阵 A A A 的迹(对角线的和)= α T β = β T α \alpha^T \beta = \beta^T \alpha αTβ=βTα,也就是内积
同时, ∣ A ∣ = |A| = ∣A∣= 对角线元素的乘积
3. A A A 的特征值为 λ 1 = tr ( A ) \lambda_1 = \text{tr}(A) λ1=tr(A),其余特征值全部为 0
4. A A A 的特征向量:
对于 λ 1 = tr ( A ) \lambda_1 = \text{tr}(A) λ1=tr(A) 对应的特征向量:
A = β α T A = \beta \alpha^T A=βαT --> A β = β α T β = tr ( A ) ⋅ β A\beta = \beta \alpha^T \beta = \text{tr}(A) \cdot \beta Aβ=βαTβ=tr(A)⋅β,所以 λ 1 = tr ( A ) \lambda_1 = \text{tr}(A) λ1=tr(A),特征向量为 k β k\beta kβ, k ≠ 0 k \neq 0 k=0
也就是说 λ 1 = tr ( A ) \lambda_1 = \text{tr}(A) λ1=tr(A) 对应的特征向量是组成 A A A 矩阵前面的列向量。
对于 λ = 0 \lambda = 0 λ=0 对应的特征向量:
A α = λ α A\alpha = \lambda \alpha Aα=λα --> A α = 0 A\alpha = 0 Aα=0,即求 A X = 0 AX = 0 AX=0 的齐次解,就是 λ = 0 \lambda = 0 λ=0 对应的特征向量

5. tr ( A ) \text{tr}(A) tr(A) 是 1 重特征值,0 是 n − 1 n - 1 n−1 重特征值
① tr ( A ) ≠ 0 \text{tr}(A) \neq 0 tr(A)=0, r ( A ) = n − r = n − 1 r(A) = n - r = n - 1 r(A)=n−r=n−1,所以当 tr ( A ) ≠ 0 \text{tr}(A) \neq 0 tr(A)=0 时,秩 1 矩阵一定能相似对角化
② tr ( A ) = 0 \text{tr}(A) = 0 tr(A)=0,这时 0 是 n n n 重特征值:
r ( A ) = n − r = n − 1 ≠ n r(A) = n - r = n - 1 \neq n r(A)=n−r=n−1=n,所以不能相似对角化
6. A n = tr ( A ) n − 1 A A^n = \text{tr}(A)^{n - 1} A An=tr(A)n−1A

例题 1:

例题 2:

补充:其他特殊矩阵
幂零矩阵:3 阶矩阵: A 3 = 0 A^3 = 0 A3=0,4 阶矩阵: A 4 = 0 A^4 = 0 A4=0
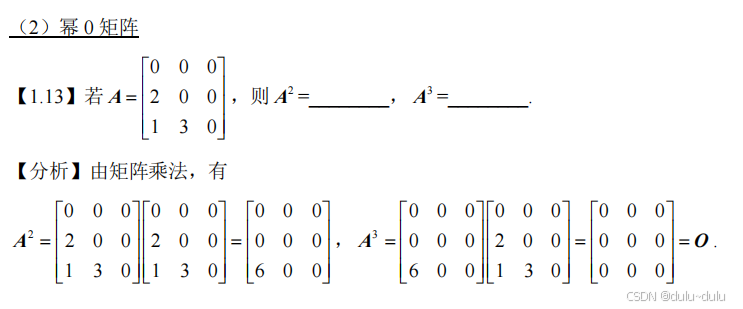



十五 关于 a B + B a aB + Ba aB+Ba(重要)


十六 同解和向量组等价


首先排除 A, C,只有行向量才和方程组的解有关系。由于 A 可由 B 线性表出,B 更具有代表性,约束更多,D 正确。

注:列向量组等价不能推出同解,行向量组等价才能推出同解。经过列变换,列向量组等价,但此时方程组的结构已经发生改变,所以解方程组只能行变换。
行向量组等价是向量组等价与方程通解的桥梁。


24 年数二:

由方程组 A x = 0 Ax = 0 Ax=0 的解均是 B T x = 0 B^T x = 0 BTx=0 的解,得 A x = 0 Ax = 0 Ax=0 与 [ A B T ] \begin{bmatrix} A \\ B^T \end{bmatrix} [ABT] x = 0 x = 0 x=0 通解。利用 r ( A ) = r ( [ A B T ] ) r(A) = r \left( \begin{bmatrix} A \\ B^T \end{bmatrix} \right) r(A)=r([ABT]) 就很好做
十七 从 A A A —> A − 1 A^{-1} A−1 原理
A A A 和 E E E 同时做初等行变换,在 A A A 化作 E E E 的同时, E E E 变为 A − 1 A^{-1} A−1

例题:


A A A 经过一系列初等行变换可变为下三角矩阵,而变化的过程就被记录在了画圈圈的部分,即画圈圈部分为 P P P

再经过初等列变换,可使 P A Q PAQ PAQ 为对角矩阵
十八 分块矩阵的初等变换
① 
② 做行变换时左乘,做列变换时右乘。
③

例题:




十九 看到就要想到

对于(1)补充一点,记住即可。

(4)的证明如下:

补充:
1.
A i j = a i j A_{ij} = a_{ij} Aij=aij --> A T = A A^T = A AT=A


A i j + a i j = 0 A_{ij} + a_{ij} = 0 Aij+aij=0 --> A T = − A A^T = -A AT=−A

除此之外,还能得到 A A A 是一个正交矩阵:
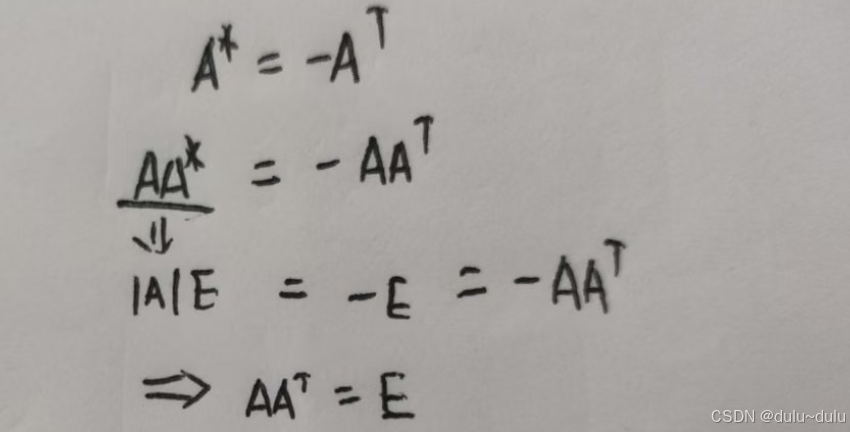

① P T A P = B P^T A P = B PTAP=B,所以 A A A 与 B B B 一定等价,且合同
② 看了上面,这里不告诉我们 P P P 可逆,我们也应该知道 P P P 矩阵可逆。 P T = P ∗ P^T = P^* PT=P∗, P P P 是正交阵,所以 A A A 与 B B B 相似。
2.
以下两题来自:
【线代救命 #5】一个视频带你拿捏矩阵相似,出题老头汗流浃背!_哔哩哔哩_bilibili

看这题需要直到,正交矩阵 Q Q Q 的特征值只能是 1 或 -1({-1,1})

3.
求 A ∗ x = 0 A^* x = 0 A∗x=0 的全部解:

对应这道题:

4. A A A 与 A T A^T AT 特征值不同,特征向量正交(重要)

相似地,可以证明 实对称矩阵不同特征值对应的特征向量相互正交。

5. A A A 可相似对角化

答案:D

6. A B AB AB 与 B A BA BA 的非零特征值相同。

由于 A B AB AB 与 B A BA BA 的非零特征值相同,所以 A B AB AB 的其中两个特征值为 1,1
又因为:

所以答案:1,1,0
二十 易错


分块矩阵
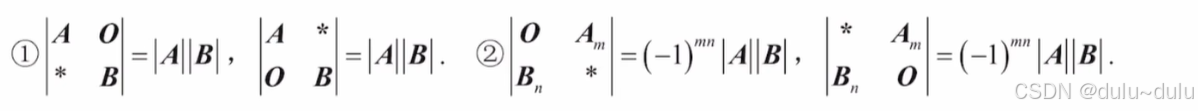
分块矩阵转置

分块矩阵求逆:副对角线求逆,分别求逆,并且对调

主副对角线求逆:

二阶求伴随:主对调,副变号

这里应该是 A B = 0 AB = 0 AB=0 不能推出 A = 0 A = 0 A=0 或 B = 0 B = 0 B=0

做题常犯错误:

-
虽然 A T A^T AT 的特征值与 A A A 相同,但特征向量不再是 ξ \xi ξ,要单独计算才能得出,要求 A T A^T AT 的特征值,只能先将 A A A 转置,然后再求特征值。

但是有一个性质:
A T A^T AT 与 A A A 属于不同特征值的特征向量正交。

-
λ 2 = 1 \lambda^2 = 1 λ2=1, λ = ± 1 \lambda = \pm 1 λ=±1,只能说 A A A 的特征值取值范围是 ${1, -1})

所以进一步可以解释这一段:
若 A A A 为正交矩阵,则其特征值的取值范围为 ${-1, 1})

25 合工大卷五 9:

答案:B
补充:
反对称矩阵的性质

Ref 1 / 3
-
线性代数 | 知识点整理 Ref 1-CSDN博客
https://blog.csdn.net/u013669912/article/details/147263380 -
线性代数 | 知识点整理 Ref 3-CSDN博客
https://blog.csdn.net/u013669912/article/details/147253667
via:
-
【数学】线性代数知识点总结-CSDN博客
https://blog.csdn.net/weixin_52924460/article/details/142375463 -
线代知识点总结_线性代数-CSDN博客
https://blog.csdn.net/weixin_69884785/article/details/139663333
相关文章:

线性代数 | 知识点整理 Ref 2
注:本文为 “线性代数 | 知识点整理” 相关文章合辑。 因 csdn 篇幅合并超限分篇连载,本篇为 Ref 2。 略作重排,未整理去重。 图片清晰度限于引文原状。 如有内容异常,请看原文。 【数学】线性代数知识点总结 阿巴 Jun 于 2024-…...
)
PyTorch深度学习框架60天进阶学习计划 - 第47天:模型压缩蒸馏技术(一)
PyTorch深度学习框架60天进阶学习计划 - 第47天:模型压缩蒸馏技术(一) 第一部分:知识蒸馏的温度调节机制详解 欢迎来到我们学习计划的第47天!今天我们将深入探讨模型压缩技术中的两个重要方法:知识蒸馏和…...

华为OD机试真题——最小的调整次数/特异性双端队列(2025A卷:100分)Java/python/JavaScript/C++/C语言/GO六种最佳实现
2025 A卷 100分 题型 本文涵盖详细的问题分析、解题思路、代码实现、代码详解、测试用例以及综合分析; 并提供Java、python、JavaScript、C、C语言、GO六种语言的最佳实现方式! 2025华为OD真题目录全流程解析/备考攻略/经验分享 华为OD机试真题《最小的调…...
)
java+postgresql+swagger-多表关联insert操作(九)
入参为json,然后根据需要对多张表进行操作: 入参格式: {"username": "车主01","usertel": "11111111111","useridtype": "2","useridcard": null,"proname&qu…...

[密码学基础]国密算法深度解析:中国密码标准的自主化之路
国密算法深度解析:中国密码标准的自主化之路 国密算法(SM系列算法)是中国自主研发的密码技术标准体系,旨在打破国际密码技术垄断,保障国家信息安全。本文将从技术原理、应用场景和生态发展三个维度,全面解…...

Flink-01学习 介绍Flink及上手小项目之词频统计
flink简介 官网 概述: 学习Flink具体包括四个关键概念:流数据的持续处理,事件时间,有状态流处理和状态快照。 Apache Flink 是一个开源的流处理框架,旨在处理批处理和实时数据处理,具有高吞吐量和低延迟的…...

自注意力机制、多头自注意力机制、填充掩码 Python实现
原理讲解 【Transformer系列(2)】注意力机制、自注意力机制、多头注意力机制、通道注意力机制、空间注意力机制超详细讲解 自注意力机制 import torch import torch.nn as nn# 自注意力机制 class SelfAttention(nn.Module):def __init__(self, input…...

目标检测篇---R-CNN梳理
目标检测系列文章 第一章 R-CNN 目录 目标检测系列文章📄 论文标题🧠 论文逻辑梳理1. 引言部分梳理 (动机与思想) 📝 三句话总结🔍 方法逻辑梳理🚀 关键创新点🔗 方法流程图补充边界框回归 (BBR)1. BBR 的…...

C#处理网络传输中不完整的数据流
1、背景 在读取byte数组的场景(例如:读取文件、网络传输数据)中,特别是网络传输的场景中,非常有可能接收了不完整的byte数组,在将byte数组转换时,因字符的缺失/增多,转为乱码。如下…...

HTML 初识
段落标签 <p><!-- 段落标签 -->Lorem ipsum dolor sit amet consectetur adipisicing elit. Fugiat, voluptate iure. Obcaecati explicabo sint ipsum impedit! Dolorum omnis voluptas sint unde sed, ipsa molestiae quo sapiente quos et ad reprehenderit.&l…...

MATLAB 训练CNN模型 yolo v4
学生对小车控制提出了更好的要求,能否加入深度学习模型。 考虑到小车用matlab来做,yolo v5及以上版本都需要在pytorch下训练,还是用早期版本来演示。 1 yolov4 调用 参考 trainYOLOv4ObjectDetector (mathworks.com) name "tiny-yo…...

【前端】跟着maxkb学习logicflow流程图画法
文章目录 背景1. 选定学习对象-maxkb应用逻辑编排2. 确定实现框架3. 关键逻辑:查看app-node.js4. 学习开始节点绘制流程数据形式 5. 给节点增加表单输入框遇到过的问题 背景 看看前端如何绘制流程图,界面好看点。 "logicflow/core": "1.…...
字符串)
数据结构-C语言版本(八)字符串
数据结构中的字符串:概念、操作与实战 第一部分 字符串的分类及常见形式 字符串是由零个或多个字符组成的有限序列,是编程中最基础也最重要的数据结构之一。 1. C语言中的字符串表示 字符数组形式 char str1[10] {H, e, l, l, o, \0};字符串字面量…...

Arduino示例代码讲解:Project 07 - Keyboard 键盘
Arduino示例代码讲解:Project 07 - Keyboard 键盘 Project 07 - Keyboard 键盘程序功能概述功能:硬件要求:输出:代码结构全局变量`setup()` 函数`loop()` 函数读取电位器值:打印电位器值:播放音调:运行过程注意事项Project 07 - Keyboard 键盘 /*Arduino Starter Kit e…...

oracle expdp/impdp 用法详解
oracle expdp/impdp 用法详解 创建逻辑目录,该命令不会在操作系统创建真正的目录,最好以system等管理员创建。 create directory db_bak as d:\test\dump; 查看管理理员目录(同时查看操作系统是否存在,因为Oracle并不关心该目录是…...

【漏洞复现】CVE-2024-38856(ApacheOfbiz RCE)
【漏洞复现】CVE-2024-38856(ApacheOfbiz RCE) 1. 漏洞描述 Apache OFBiz 是一个开源的企业资源规划(ERP)系统。它提供了一套企业应用程序,用于集成和自动化企业的许多业务流程。 这个漏洞是由于对 CVE-2023-51467 的…...

超详细VMware虚拟机扩容磁盘容量-无坑版
1.环境: 虚拟机:VMware Workstation 17 Pro-17.5.2 Linux系统:Ubuntu 22.04 LTS 2.硬盘容量 虚拟机当前硬盘容量180G -> 扩展至 300G 3.操作步骤 (1)在虚拟机关机的状态下,虚拟机硬盘扩容之前必…...

每日一题算法——移除链表元素、反转链表
移除链表元素 力扣题目链接 我的解法: 注意细节:要删掉移除的元素。 class Solution { public:ListNode* removeElements(ListNode* head, int val) {while(head!nullptr){if(head->valval){headhead->next;}}ListNode* nowhead head;while(n…...

全面理解Linux 系统日志:核心文件与查看方法
全文目录 1 Linux 系统日志分类及功能1.1 通用日志1.1.1 /var/log/messages1.1.2 /var/log/syslog 1.2 安全相关日志1.2.1 /var/log/auth.log(Debian/Ubuntu)或 /var/log/secure(RHEL/CentOS)1.2.2 /var/log/audit/au…...

机器学习-08-关联规则更新
总结 本系列是机器学习课程的系列课程,主要介绍机器学习中关联规则和协同过滤。 参考 机器学习(三):Apriori算法(算法精讲) Apriori 算法 理论 重点 【手撕算法】【Apriori】关联规则Apriori原理、代码…...

Flutter与FastAPI的OSS系统实现
作者:孙嘉成 目录 一、对象存储 二、FastAPI与对象存储 2.1 缤纷云S4服务API对接与鉴权实现 2.2 RESTful接口设计与异步路由优化 三、Flutter界面与数据交互开发 3.1 应用的创建 3.2页面的搭建 3.3 文件的上传 关键词:对象存储、FastAPI、Flutte…...

Kubernetes控制平面组件:API Server详解(二)
云原生学习路线导航页(持续更新中) kubernetes学习系列快捷链接 Kubernetes架构原则和对象设计(一)Kubernetes架构原则和对象设计(二)Kubernetes架构原则和对象设计(三)Kubernetes控…...

MySQL-锁机制3-意向共享锁与意向排它锁、死锁
文章目录 一、意向锁二、死锁应该如何避免死锁问题? 总结 一、意向锁 在表获取共享锁或者排它锁时,需要先检查该表有没有被其它事务获取过X锁,通过意向锁可以避免大量的行锁扫描,提升表获取锁的效率。意向锁是一种表级锁…...

报告系统状态的连续日期 mysql + pandas(连续值判断)
本题用到知识点:row_number(), union, date_sub(), to_timedelta()…… 目录 思路 pandas Mysql 思路 链接:报告系统状态的连续日期 思路: 判断连续性常用的一个方法,增量相同的两个列的差值是固定的。 让日期与行号 * 天数…...

pytest自动化中关于使用fixture是否影响用例的独立性
第一个问题:难道使用fixture 会影响用例独立吗? ✅ 简单回答: 使用 fixture ≠ 不独立。 只要你的 fixture 是每次测试都能自己运行、自己产生数据的,那么测试用例依然是“逻辑独立”的。 ✅ 怎么判断 fixture 是否影响独立性&a…...

Token与axios拦截器
目录 一、Token 详解 1. Token 的定义与作用 2. Token 的工作流程 3. Token 的优势 4. Token 的安全实践 5. JWT 结构示例 二、Axios 拦截器详解 1. 拦截器的作用 2. 请求拦截器 3. 响应拦截器 4. 拦截器常见场景 5. 移除拦截器 三、完整代码示例 四、总结 五、…...

unity3d实现物体闪烁
unity3d实现物体闪烁,代码如下: using UnityEngine;public class Test : MonoBehaviour {//创建一个常量,用来接收时间的变化值private float shake;//通过控制物体的MeshRenderer组件的开关来实现物体闪烁的效果private MeshRenderer BoxColliderClick…...
)
C#—Lazy<T> 类型(延迟初始化/懒加载模式)
C# 的 Lazy<T> 类型 Lazy<T> 是 C# 中的一个类,用于实现延迟初始化(懒加载)模式。它提供了一种线程安全的方式来延迟创建大型或资源密集型对象,直到第一次实际需要时才进行初始化。 主要特点 延迟初始化:…...

Spring Boot 项目启动命令解析
Spring Boot 项目启动命令参数 一、启动命令基础格式 java [JVM参数] [Spring Boot参数] -jar your-project.jar必选部分:java -jar your-project.jar 启动可执行 JAR 包。 可选部分: JVM 参数:控制 Java 虚拟机行为(如内存、垃…...
?及 `docker run` 详细执行过程)
为什么 Docker 容器中有额外的目录(如 `/dev`、`/proc`、`/sys`)?及 `docker run` 详细执行过程
、当你使用 docker run 启动一个基于极简镜像(如 scratch 或手动构建的镜像)的容器时,发现容器内出现了 /dev、/proc、/sys 等目录,即使你的镜像中并未包含这些目录。这是因为 Docker 在启动容器时,会自动挂载一些必要…...

