神经网络的 “成长密码”:正向传播与反向传播深度解析(四)
引言
在神经网络的神秘世界里,正向传播和反向传播是驱动模型学习和进化的核心机制。它们如同神经网络的 “左右脑”,正向传播负责信息的前向流动与初步处理,反向传播则通过优化权重参数来提升模型性能,二者相辅相成,共同构建了神经网络强大的学习能力。今天,就让我们深入探索这两种关键过程,揭开神经网络高效学习的秘密。
一、正向传播:信息的前向之旅
(一)正向传播的定义与流程
正向传播是神经网络中信息从输入层开始,依次经过隐藏层,最终到达输出层的传递过程。在这个过程中,输入数据首先会在神经元中进行线性加权组合。假设神经元的输入为\(x_1, x_2, \cdots, x_n\),对应的权重为\(w_{1}, w_{2}, \cdots, w_{n}\),偏置为b,那么线性加权组合的结果\(z = w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{n}x_{n} + b\)。之后,z会经过激活函数f进行非线性变换,得到神经元的输出\(a = f(z)\) 。这样的计算过程在隐藏层和输出层的每个神经元中依次进行,信息就像接力赛中的接力棒一样,在不同层之间逐层向前传递,最终得到网络的输出结果 。
(二)神经网络的结构与正向传播的关系
神经网络的结构通常包含输入层、隐藏层和输出层。虽然理论上神经网络允许跳层连接(如残差网络中的跳跃连接),但一般不允许横向和倒着连接。这种结构设计保证了信息在正向传播过程中的有序流动,使得网络能够按照特定的逻辑对输入数据进行逐步处理。输入层负责接收外部数据,隐藏层通过层层的线性加权和激活函数变换,对数据进行特征提取和抽象,输出层则根据隐藏层的处理结果给出最终的预测或分类输出 。
二、神经网络的训练之旅:从随机到精准
(一)训练的起点与目标
神经网络在训练开始时,其权重参数是随机初始化的。这就意味着在初始阶段,网络的输出结果往往与真实值相差甚远,就像一个刚接触新知识的学习者,对问题的判断可能并不准确。而训练的目的,就是要赋予神经网络自我更新和学习的能力,通过不断调整权重参数,让网络的输出能够尽可能地接近真实值,实现完美的输出效果 。
(二)梯度下降法:训练的有力武器
在神经网络的训练过程中,梯度下降法是优化权重参数的核心方法。它的基本思想是通过计算损失函数关于权重参数的偏导数,来确定权重参数的更新方向。简单来说,就是朝着损失函数值下降最快的方向去调整权重,就好比在下山时,总是沿着坡度最陡的方向前进,这样能最快地到达山底 。通过不断地迭代更新权重参数,使得损失函数值逐渐减小,网络的性能也随之不断提升 。
三、反向传播:误差的逆向溯源与参数优化
(一)反向传播算法示例
以一个简单的两层神经元网络为例来详细说明反向传播过程。假设网络的输入为x,第一层神经元的权重为\(w_{1}\),第二层神经元的权重为\(w_{2}\),输出为y,真实值为\(y_{true}\) 。首先进行正向传播得到网络输出y,然后计算损失函数\(L(y, y_{true})\),比如采用欧式距离作为损失函数,即\(L=\frac{1}{2}(y - y_{true})^2\) 。
反向传播从输出层开始,计算损失函数对输出层神经元权重的偏导数\(\frac{\partial L}{\partial w_{2}}\) 。根据链式法则,\(\frac{\partial L}{\partial w_{2}}=\frac{\partial L}{\partial y}\frac{\partial y}{\partial w_{2}}\) 。这里,\(\frac{\partial L}{\partial y}\)表示损失函数对输出的导数,\(\frac{\partial y}{\partial w_{2}}\)表示输出对权重\(w_{2}\)的导数。计算出\(\frac{\partial L}{\partial w_{2}}\)后,就可以根据梯度下降法的规则来更新权重\(w_{2}\),例如\(w_{2}=w_{2}-\eta\frac{\partial L}{\partial w_{2}}\),其中\(\eta\)是学习率,控制着权重更新的步长 。
接着,将误差(损失函数对输出的导数)通过链式法则逐层向后传递到第一层神经元,计算\(\frac{\partial L}{\partial w_{1}}\) 。同样根据链式法则,\(\frac{\partial L}{\partial w_{1}}=\frac{\partial L}{\partial y}\frac{\partial y}{\partial a_{1}}\frac{\partial a_{1}}{\partial w_{1}}\),其中\(a_{1}\)是第一层神经元的输出。计算出\(\frac{\partial L}{\partial w_{1}}\)后,更新权重\(w_{1}\) 。
(二)反向传播的核心原理与计算公式
反向传播的核心就是利用链式法则实现误差的逆向分解,计算损失函数关于各个权重参数的偏导数。对于一般的神经网络,假设网络有L层,第l层的权重为\(W^{l}\),输入为\(a^{l - 1}\),输出为\(a^{l}\),激活函数为\(f^{l}\) 。那么,损失函数L对\(W^{l}\)的偏导数计算公式为:
\(\frac{\partial L}{\partial W^{l}}=\frac{\partial L}{\partial a^{L}}\prod_{k = l}^{L - 1}\frac{\partial a^{k + 1}}{\partial a^{k}}\frac{\partial a^{k}}{\partial W^{l}}\)
通过这样的计算,能够精确地得到每个权重参数对损失函数的影响程度,从而根据梯度下降法的规则,沿着梯度的反方向更新权重参数,使得损失函数值不断减小,实现网络的优化 。
(三)激活函数可导的重要性
在反向传播过程中,激活函数必须是可导的。因为在利用链式法则计算偏导数时,需要对激活函数求导。如果激活函数不可导,就无法按照链式法则计算损失函数对权重参数的偏导数,也就无法进行反向传播和权重更新 。例如,ReLU 函数(\(f(x)=\max(0, x)\))在\(x > 0\)时导数为 1,\(x \leq 0\)时导数为 0,这种可导性使得它在神经网络中被广泛应用;而像符号函数(\(sgn(x)=\begin{cases}1, & x > 0 \\ 0, & x = 0 \\ -1, & x < 0\end{cases}\))在\(x = 0\)处不可导,就不适合直接作为神经网络中的激活函数 。
四、面试常见问题及解析
问题 1:请简要描述正向传播和反向传播的过程。
解析:正向传播是信息从输入层流向输出层的过程。输入数据在神经元中进行线性加权组合,再经过激活函数处理,逐层向前传递,最终得到网络输出 。反向传播则从输出层开始,计算损失函数关于权重参数的偏导数,利用链式法则将误差逐层向后传递,根据偏导数更新权重参数,使得损失函数值不断减小,优化网络性能 。
问题 2:为什么激活函数需要可导?
解析:因为在反向传播过程中,要使用链式法则计算损失函数对权重参数的偏导数,这就要求激活函数可导。只有激活函数可导,才能在链式法则的计算中包含激活函数的导数项,从而准确计算出每个权重参数对损失函数的影响,进而根据梯度下降法更新权重参数 。如果激活函数不可导,就无法进行反向传播和权重更新,神经网络也就无法通过训练优化性能 。
问题 3:在反向传播中,链式法则起到了什么作用?
解析:链式法则在反向传播中起着核心作用。它使得误差能够从输出层开始,沿着网络的层次结构逐层向后传递,分解计算出损失函数对每一层权重参数的偏导数 。通过链式法则,将复杂的损失函数偏导数计算转化为多个简单导数的乘积,从而实现对权重参数的精确调整,保证了神经网络能够根据误差反馈有效地更新权重,优化网络性能 。
问题 4:梯度下降法在神经网络训练中是如何工作的?
解析:梯度下降法通过计算损失函数关于权重参数的偏导数,确定权重参数的更新方向。在每次迭代中,沿着损失函数梯度的反方向更新权重参数,更新公式为\(w = w - \eta\frac{\partial L}{\partial w}\),其中w是权重参数,\(\eta\)是学习率,\(\frac{\partial L}{\partial w}\)是损失函数对权重的偏导数 。通过不断迭代,逐步减小损失函数值,使网络输出不断接近真实值,实现神经网络的训练和优化 。
五、总结
正向传播和反向传播是神经网络训练过程中不可或缺的两个环节。正向传播负责信息的初步处理和输出,反向传播则通过误差的逆向传播和权重参数的优化,让神经网络能够不断学习和改进。理解这两个过程,以及与之相关的梯度下降法、损失函数和激活函数的原理,是掌握神经网络技术的关键 。希望通过本文的解析,能帮助大家在神经网络的学习道路上更进一步,在实际应用中更好地运用这一强大的技术 。
相关文章:
)
神经网络的 “成长密码”:正向传播与反向传播深度解析(四)
引言 在神经网络的神秘世界里,正向传播和反向传播是驱动模型学习和进化的核心机制。它们如同神经网络的 “左右脑”,正向传播负责信息的前向流动与初步处理,反向传播则通过优化权重参数来提升模型性能,二者相辅相成,共…...

Mujoco robosuite 机器人模型
import ctypes import os# 获取当前脚本所在的目录 script_dir os.path.dirname(os.path.abspath(__file__))# 构建库文件的相对路径 lib_relative_path os.path.join(dynamic_models, UR5e, Jb.so)# 拼接成完整的路径 lib_path os.path.join(script_dir, lib_relative_path…...

在Ubuntu 18.04下编译OpenJDK 11
在Ubuntu 18.04下编译OpenJDK 11 源码下载地址: 链接: https://pan.baidu.com/s/1QAdu-B6n9KqeBakGlpBS3Q 密码: 8lho Linux下的环境要求 不同版本的jdk会要求在不同版本的Ubuntu下编译,不要用太高版本的Ubuntu或者gcc,特别是gcc…...

K8s:概念、特点、核心组件与简单应用
一、引言 在当今云计算和容器技术蓬勃发展的时代,Kubernetes(简称 K8s)已成为容器编排领域的事实标准。它为管理容器化应用提供了高效、可靠的解决方案,极大地简化了应用的部署、扩展和运维过程。无论是小型初创公司还是大型企业…...

STM32的定时器输出PWM时,死区时间(DTR)如何计算
在 STM32F429(以及所有 STM32F4 “高级定时器”)中,死区时间由 TIMx_BDTR 寄存器的 8 位 “Dead‑Time Generator” 字段 DTG[7:0] 来配置。其计算分三步: 计算死区时钟周期 tDTS TIM1 时钟源为 APB2 定时器时钟(PCL…...

STC32G12K128单片机GPIO模式SPI操作NorFlash并实现FatFS文件系统
STC32G12K128单片机GPIO模式SPI操作NorFlash并实现FatFS文件系统 NorFlash简介NorFlash操作驱动代码文件系统测试代码 NorFlash简介 NOR Flash是一种类型的非易失性存储器,它允许在不移除电源的情况下保留数据。NOR Flash的名字来源于其内部结构中使用的NOR逻辑门。…...

ClickHouse 设计与细节
1. 引言 ClickHouse 是一款备受欢迎的开源列式在线分析处理 (OLAP) 数据库管理系统,专为在海量数据集上实现高性能实时分析而设计,并具备极高的数据摄取速率 1。其在各种行业中得到了广泛应用,包括众多知名企业,例如超过半数的财…...

MySQL基础安装和学习
MySQL 是一种开源的关系型数据库管理系统(RDBMS),由瑞典公司 MySQL AB 开发,后被 Oracle 公司收购。它是一种基于客户端/服务器架构的数据库系统,广泛应用于 Web 应用开发和企业级数据管理。 MySQL 使用 SQL(Structured Query Language,结构化查询语言)作为与数据库交…...

智能体MCP 实现数据可视化分析
参考: 在线体验 https://www.doubao.com/chat/ 下载安装离线体验 WPS软件上的表格分析 云上创建 阿里mcp:https://developer.aliyun.com/article/1661198 (搜索加可视化) 案例 用cline 或者cherry studio实现 mcp server:excel-mcp-server、quickchart-mcp-server...

再看开源多模态RAG的视觉文档(OCR-Free)检索增强生成方案-VDocRAG
前期几个工作提到,基于OCR的文档解析RAG的方式进行知识库问答,受限文档结构复杂多样,各个环节的解析泛化能力较差,无法完美的对文档进行解析。因此出现了一些基于多模态大模型的RAG方案。如下: 【RAG&多模态】多模…...

生产环境大数据平台权限管理
引言:数据资产保护的生死线 在金融行业某头部企业发生的数据泄露事件中,由于权限管理漏洞导致千万级用户信息外泄,直接经济损失超过2.3亿元。这个案例揭示了生产环境大数据平台权限管理的重要性和复杂性。本文将深入探讨从权限模型设计到实施…...

深入浅出 NVIDIA CUDA 架构与并行计算技术
🐇明明跟你说过:个人主页 🏅个人专栏:《深度探秘:AI界的007》 🏅 🔖行路有良友,便是天堂🔖 目录 一、引言 1、CUDA为何重要:并行计算的时代 2、NVIDIA在…...

FPGA系列之DDS信号发生器设计(DE2-115开发板)
一、IP核 IP(Intellectual Property)原指知识产权、著作权等,在IC设计领域通常被理解为实现某种功能的设计。IP模块则是完成某种比较复杂算法或功能(如FIR滤波器、FFT、SDRAM控制器、PCIe接口、CPU核等)并且参数可修改的电路模块,…...

Rust: 从内存地址信息看内存布局
内存布局其实有几个:address(地址)、size(大小)、alignment(对齐位数,2 的自然数次幂,2,4,8…)。 今天主要从address来看内存的布局。 说明&…...

【Dv3Admin】从零搭建Git项目安装·配置·初始化
项目采用 Django 与 Vue3 技术栈构建,具备强大的后端扩展能力与现代前端交互体验。完整实现了权限管理、任务队列、WebSocket 通信、系统配置等功能,适用于构建中后台管理系统与多租户平台。 本文章内容涵盖环境搭建、虚拟环境配置、前后端部署、项目结…...

P3416-图论-法1.BFS / 法2.Floyd
这道题虽然标签有floyd但是直接bfs也能过 其实事实证明还是bfs快,因为bfs只需要遍历特定的点,但是floyd需要考虑遍历所有可能的中介点 法1.BFS 用字典存储每个点所能普及的范围,然后用对每个点bfs进行拓展 nint(input())temp[]#xmax0;yma…...

极狐GitLab 议题和史诗创建的速率限制如何设置?
极狐GitLab 是 GitLab 在中国的发行版,关于中文参考文档和资料有: 极狐GitLab 中文文档极狐GitLab 中文论坛极狐GitLab 官网 议题和史诗创建的速率限制 (BASIC SELF) 速率限制是为了控制新史诗和议题的创建速度。例如,如果您将限制设置为 …...

提交到Gitee仓库
文章目录 注册配置公钥创建空白的码云仓库把本地项目上传到码云对应的空白仓库中 注册 注册并激活码云账号( 注册页面地址:https://gitee.com/signup ) 可以在自己C盘/用户/用户名/.ssh 可以看到 有id_rsa.pub 以前在GitHub注册时搞过&…...
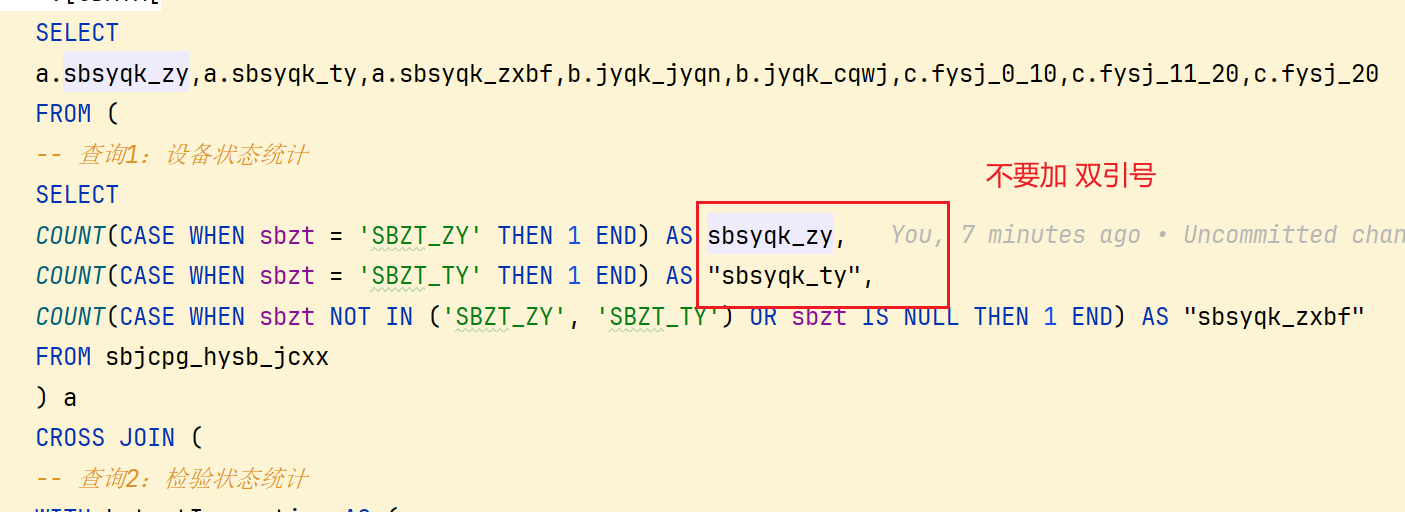
oracle中错误总结
oracle中给表起别名不能用as,用as报错 在 Oracle 数据库中,WITH 子句(即 CTE,公共表表达式)允许后续定义的子查询引用前面已经定义的 CTE,但 前面的 CTE 无法引用后面的 CTE。这种设计类似…...

纽约大学具身智能体在城市空间中的视觉导航之旅!CityWalker:从海量网络视频中学习城市导航
作者:Xinhao Liu, Jintong Li, Yicheng Jiang, Niranjan Sujay, Zhicheng Yang, Juexiao Zhang, John Abanes, Jing Zhang, Chen Feng单位:纽约大学论文标题:CityWalker: Learning Embodied Urban Navigation from Web-Scale Videos论文链接&…...

Go语言中 defer 使用场景及深度注意事项指南
文章精选推荐 1 JetBrains Ai assistant 编程工具让你的工作效率翻倍 2 Extra Icons:JetBrains IDE的图标增强神器 3 IDEA插件推荐-SequenceDiagram,自动生成时序图 4 BashSupport Pro 这个ides插件主要是用来干嘛的 ? 5 IDEA必装的插件&…...

OpenCV颜色变换cvtColor
OpenCV计算机视觉开发实践:基于Qt C - 商品搜索 - 京东 颜色变换是imgproc模块中一个常用的功能。我们生活中看到的大多数彩色图片都是RGB类型的,但是在进行图像处理时需要用到灰度图、二值图、HSV(六角锥体模型,这个模型中颜色的…...

Manus技术架构、实现内幕及分布式智能体项目实战
Manus技术架构、实现内幕及分布式智能体项目实战 模块一: 剖析Manus分布式多智能体全生命周期、九大核心模块及MCP协议,构建低幻觉、高效且具备动态失败处理能力的Manus系统。 模块二: 解析Manus大模型Agent操作电脑的原理与关键API…...

下载油管视频 - yt-dlp
文章目录 1. yt-dlp与you-get介绍1.1 主要功能对比1.2 使用场景1.3 安装 2. 基本命令介绍2.1 默认下载视频2.2 指定画质和格式规则2.3 下载播放列表2.4 备注 3. 参考资料 之前只使用you-get下载b站视频,当时了解you-get也可下载油管视频,但之前无此需求&…...

济南通过首个备案生活服务大模型,打造行业新标杆
近日,一则振奋人心的消息在人工智能领域传开:济南本土企业丽阳神州智能科技有限公司自主研发的 “丽阳雨露” 大模型成功通过国家网信办的备案。这一成果不仅是济南企业在科技创新道路上的重大突破,更标志着我国在生活服务领域的人工智能应用…...

系统架构师2025年论文《论软件三层结构的设计》
论软件三层结构的设计 摘要: 我所在的单位是某市主要医院之一,作为单位的主要技术骨干,2009 年 1 月,我主持了某市医院预约挂号系统的开发,该系统是医院信息化管理系统的一个子系统,由于医院系统对安全性、可靠性、可用性和响应速度要求很高,我选择了三层 C/S 结构作为…...

第6次课 贪心算法 A
向日葵朝着太阳转动,时刻追求自身成长的最大可能。 贪心策略在一轮轮的简单选择中,逐步导向最佳答案。 课堂学习 引入 贪心算法(英语:greedy algorithm),是用计算机来模拟一个「贪心」的人做出决策的过程…...

C# 高级编程:Lambda 表达式
在 C# 的高级编程中,Lambda 表达式是一个强大而灵活的工具,广泛应用于 LINQ 查询、委托、事件处理以及函数式编程等多个领域。它不仅使代码更简洁、表达更直接,而且在某些场景中能极大提高代码的可读性与可维护性。本文将从 Lambda 表达式的基本语法入手,深入探讨其原理、常…...
Hexo+Github+gitee图床零成本搭建自己的专属博客
一个详细、完善的 Hexo 博客部署教程,不仅涵盖了基本的安装、配置、生成与部署步骤,还增加了常见问题的解决、主题设置、图片上传等 在开始之前可以看看我最终搭建出来的成果:https://liangjh.blog 1.安装git和nodejs 在Windows上使用Git&a…...

数字信号处理技术架构与功能演进
数字信号处理(DSP)是通过数字运算实现信号分析、变换、滤波及调制解调的技术领域,其发展过程与技术应用如下: 一、定义与核心功能 技术定义:通过算法将模拟信号转换为数字形式进行处理,具有高精度、可编程…...
