数据结构初阶：二叉树（四）

概述：本篇博客主要介绍链式结构二叉树的实现。

目录

1.实现链式结构二叉树

1.1 二叉树的头文件（tree.h）

1.2 创建二叉树 

 1.3 前中后序遍历

1.3.1 遍历规则 

1.3.1.1 前序遍历代码实现

1.3.1.2  中序遍历代码实现

1.3.1.3  后序遍历代码实现

 1.4 二叉树结点的个数

 1.5 二叉树叶子结点个数

1.6  二叉树第k层结点个数

1.7  二叉树的深度/高度

​编辑

 1.8 查找值为x的结点

1.9 二叉树的销毁 

2. 小结 

---

1.实现链式结构二叉树

1.1 二叉树的头文件（tree.h）

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//定义链式结构二叉树
//二叉树结点的结构
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//前序遍历
void preOrder(BTNode* root);
//中序遍历
void InOrder(BTNode* root);
//后序遍历
void postOrder(BTNode* root);//二叉树结点个数
int BinaryTreeSize(BTNode* root);
//void BinaryTreeSize(BTNode* root,int* psize);//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root);//二叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k);//二叉树的深度/高度
int BinaryTreeDepth(BTNode* root);//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);//二叉树销毁
void BinaryTreeDestroy(BTNode** root);//层序遍历
void LevelOrder(BTNode* root);//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);

1.2 创建二叉树 

 用链表来表示一颗二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址，其结构如下：

//定义链式结构二叉树
//二叉树结点的结构
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;  // 指向当前结点左孩子struct BinaryTreeNode* right; // 指向当前结点右孩子
}BTNode;

二叉树的创建方式比较复杂，为了更好走进二叉树的学习中，我们先手动构建一颗链式二叉树。 

#include"Tree.h"
BTNode* buyNode(char x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->data = x;node->left = node->right = NULL;return node;
}
BTNode* creatBinaryTree()
{BTNode* nodeA = buyNode('A');BTNode* nodeB = buyNode('B');BTNode* nodeC = buyNode('C');BTNode* nodeD = buyNode('D');BTNode* nodeE = buyNode('E');BTNode* nodeF = buyNode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->left = nodeE;nodeC->right = nodeF;return nodeA;
}

回顾二叉树的概念，二叉树分为空树和非空二叉树，非空二叉树由根结点根结点的左子树、根结点的右子树组成的。 

 

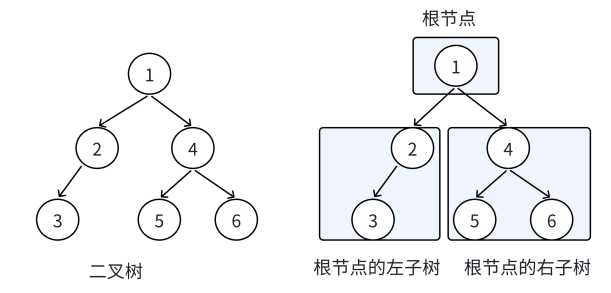
 根结点的左子树和右子树分别又是由子树结点、子树结点的左子树、子树结点的右子树组成的，因此二叉树定义式递归式的，后续链式二叉树的操作基本都是按照该概念实现的。

 1.3 前中后序遍历

二叉树的操作离不开树的遍历，我们先来看一下二叉树的遍历有哪些方式。 

 

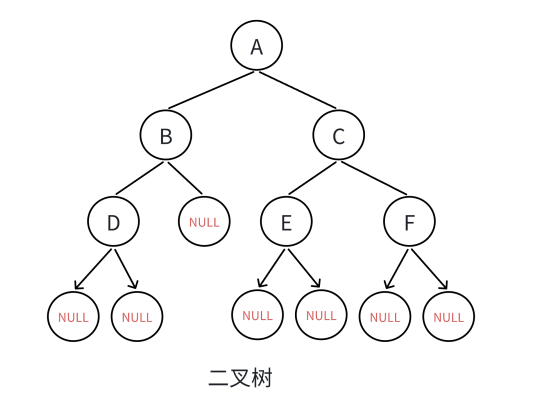
1.3.1 遍历规则 

 按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1）前序遍历(Preorder Traversal 亦称先序遍历)：访问根结点的操作发生在遍历其左右子树之前

访问顺序为：根结点、左子树、右子树

 2）中序遍历(Inorder Traversal)：访问根结点的操作发⽣在遍历其左右子树之中（间）

访问顺序为：左子树、根结点、右子树 

3）后序遍历(Postorder Traversal)：访问根结点的操作发生在遍历其左右子树之后

 访问顺序为：左子树、右子树、根结点

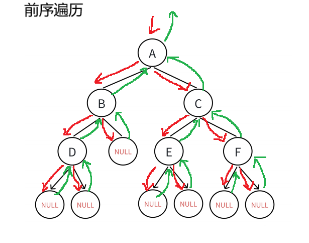
1.3.1.1 前序遍历代码实现

void preOrder(BTNode* root)
{if(root == NULL){printf("NULL ");return;}printf("%c ", root->data);preOrder(root->left);preOrder(root->right);
}

逻辑概述： 

 这段 代码定义了一个先序遍历二叉树的函数 `preOrder`。函数的参数是一个指向二叉树节点的指针 `root`。

如果 `root` 为空，函数会输出 `NULL` 并返回。否则，函数会先输出当前节点的数据，然后对左子树和右子树分别递归调用 `preOrder` 函数进行先序遍历。

在代码中，`printf("%c ", root->data);` 用于输出当前节点的数据，假设 `data` 是字符类型。 

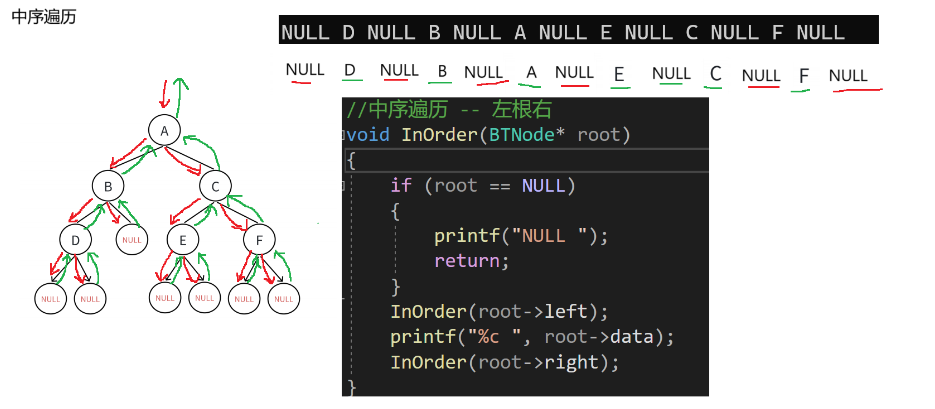
1.3.1.2  中序遍历代码实现

void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}

逻辑概述： 

这段代码是一个二叉树的中序遍历函数。其功能是：如果根节点为空，输出"NULL "并返回；否则，先对左子树进行中序遍历，然后输出根节点的数据，最后对右子树进行中序遍历。其实现过程与常见的二叉树中序遍历的逻辑一致。 

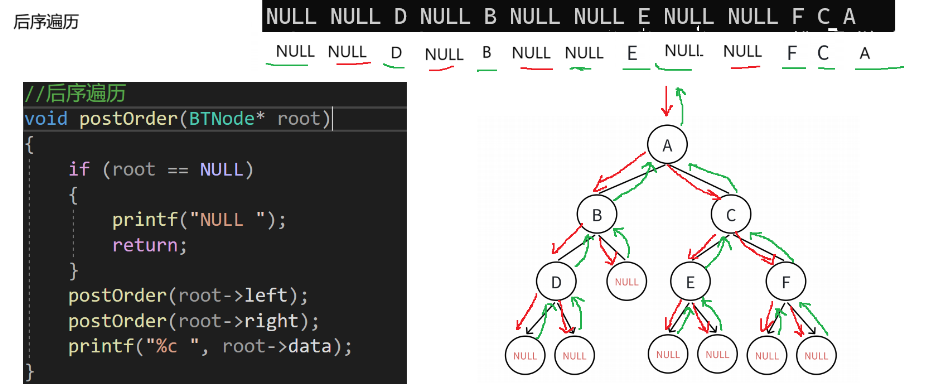
1.3.1.3  后序遍历代码实现

void postOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}postOrder(root->left);postOrder(root->right);printf("%c ", root->data);
}

逻辑概述： 

 这段代码定义了一个二叉树的后序遍历函数 `postOrder` 。函数的作用是：如果根节点为空，输出 `"NULL "` 并返回；否则，先对左子树进行后序遍历，再对右子树进行后序遍历，最后输出根节点的数据。这符合二叉树后序遍历的逻辑，即先遍历左子树，再遍历右子树，最后访问根节点。 

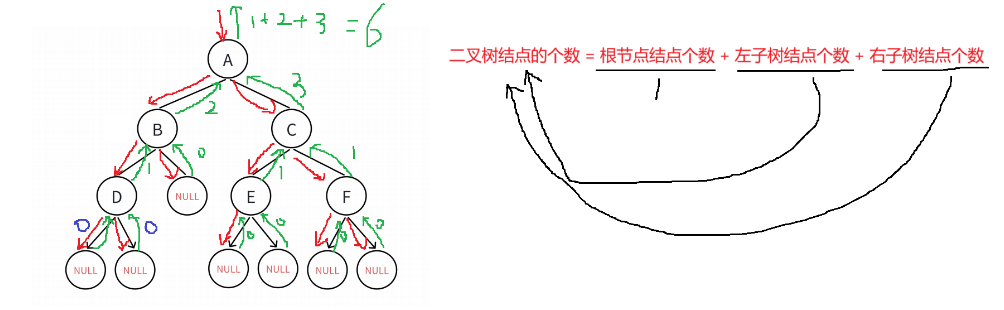
 1.4 二叉树结点的个数

int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return 1 + BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

逻辑概述： 

 这段代码定义了一个计算二叉树节点个数的函数 `BinaryTreeSize` 。

函数的逻辑是：如果根节点为空，返回 0；如果根节点的左右子树都为空，返回 1；否则，返回 1 加上左子树的节点个数和右子树的节点个数。其中，左子树和右子树的节点个数通过递归调用 `BinaryTreeLeafSize` 函数来计算。 

 

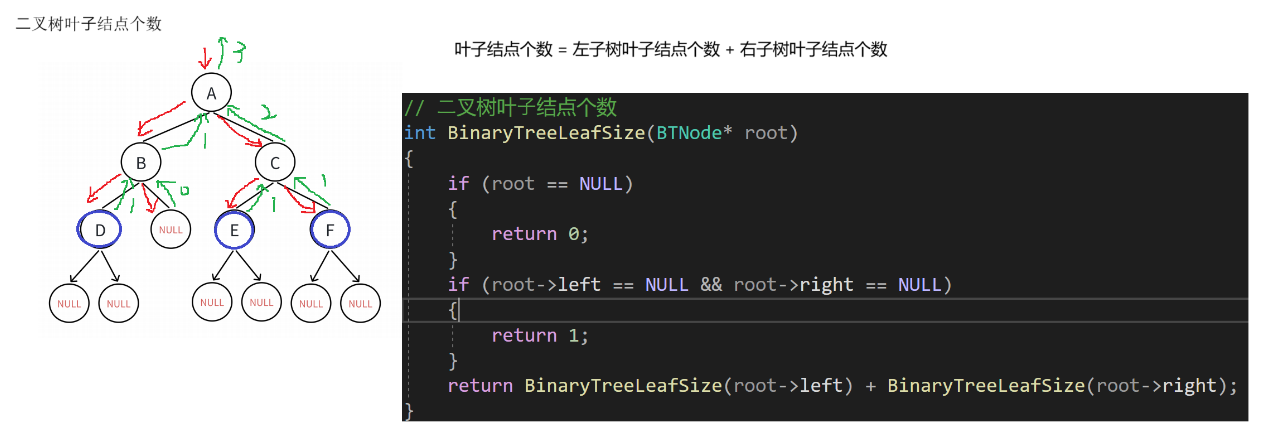
 1.5 二叉树叶子结点个数

//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

 逻辑概述：

 这段代码定义了一个计算二叉树叶子结点个数的函数`BinaryTreeLeafSize`。

函数的逻辑是：如果根节点为空，返回0；如果根节点的左右子树都为空，说明该节点为叶子节点，返回1；否则，通过递归调用函数本身，分别计算左子树和右子树的叶子节点个数，并将它们相加后返回。 

1.6  二叉树第k层结点个数

// 计算二叉树第 k 层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL) {return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

 逻辑概述：

这段代码的功能是计算二叉树中第k层的节点个数。如果根节点为空，返回0。如果k等于1，说明当前根节点就是第k层的节点，返回1。否则，通过递归调用函数本身，分别计算左子树和右子树中第k - 1层的节点个数，并将它们相加后返回。

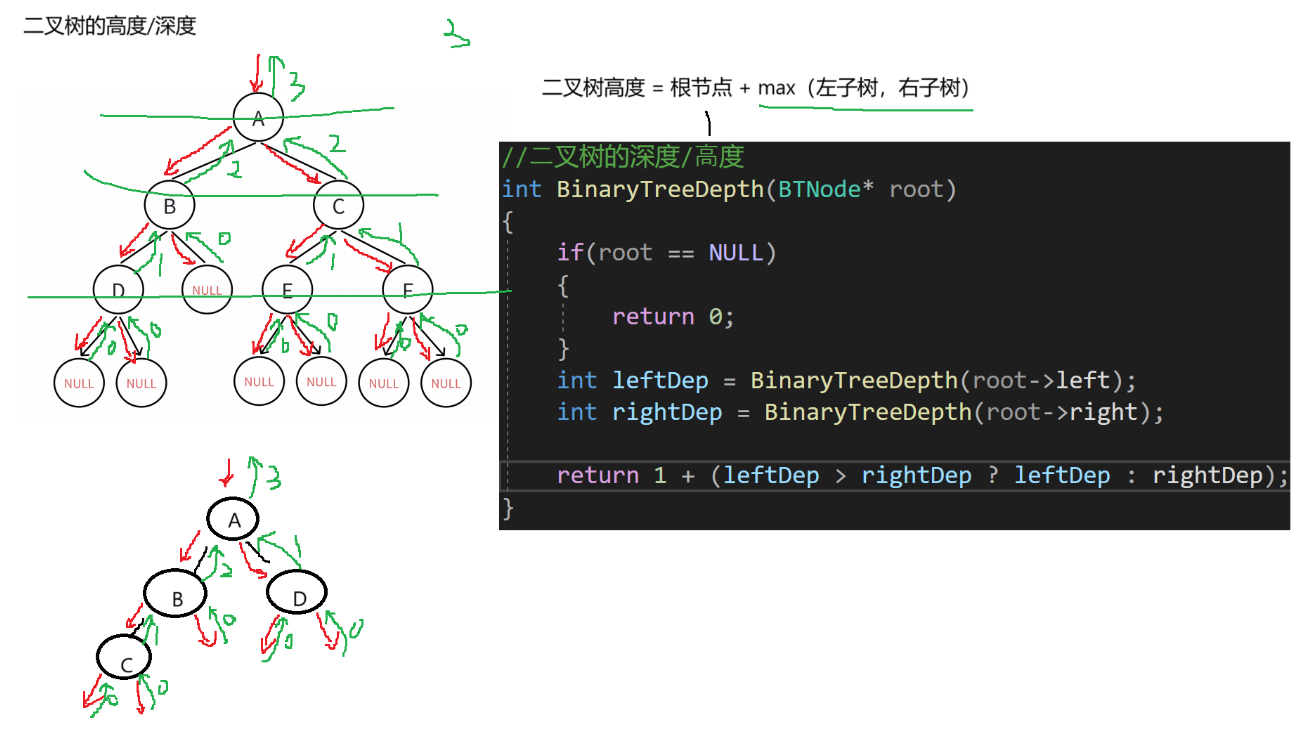
1.7  二叉树的深度/高度

//二叉树的深度/高度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDep = BinaryTreeDepth(root->left);int rightDep = BinaryTreeDepth(root->right);return 1 + (leftDep > rightDep ? leftDep : rightDep);
}

逻辑概述： 

 这段代码定义了一个计算二叉树深度（高度）的函数 `BinaryTreeDepth` 。

函数的逻辑是：如果根节点为空，返回 0 。然后分别计算左子树和右子树的深度，记为 `leftDep` 和 `rightDep` 。最后，二叉树的深度为 1 加上 `leftDep` 和 `rightDep` 中的较大值。 

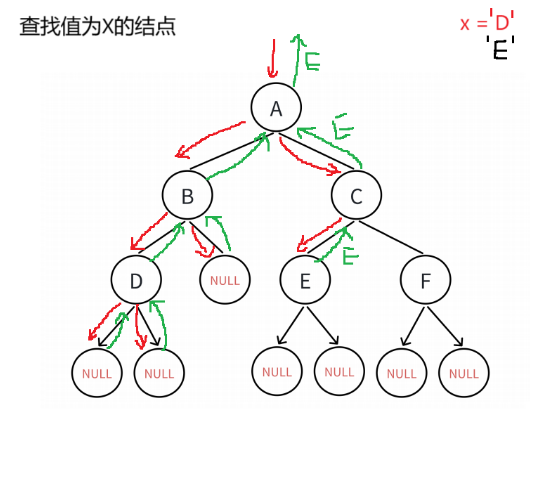
 1.8 查找值为x的结点

//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* leftFind = BinaryTreeFind(root->left, x);if (leftFind){return leftFind;}BTNode* rightFind = BinaryTreeFind(root->right, x);if (rightFind){return rightFind;}return NULL;
}

逻辑概述： 

 这段代码定义了一个在二叉树中查找值为`x`的节点的函数`BinaryTreeFind`。

函数的执行过程如下：
- 如果根节点为空，直接返回`NULL`，表示未找到。
- 如果根节点的值等于`x`，则返回根节点。
- 然后在左子树中递归查找值为`x`的节点，如果找到则返回该节点。
- 如果在左子树中未找到，再在右子树中递归查找值为`x`的节点，如果找到则返回该节点。
- 如果在整个二叉树中都未找到值为`x`的节点，则最终返回`NULL`。 

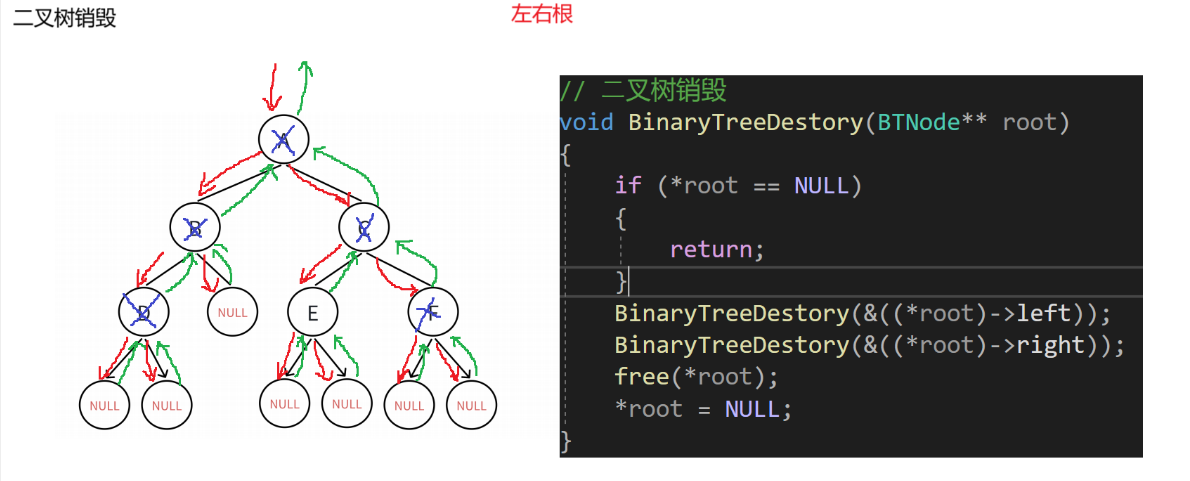
1.9 二叉树的销毁 

//二叉树销毁
void BinaryTreeDestroy(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestroy(&((*root)->left));BinaryTreeDestroy(&((*root)->right));*root == NULL;
}

2. 小结 

以上便是本篇博客的所有内容了，如果这篇博客能给大家带来知识，还请大家多多点赞。