二分小专题
P1102 A-B 数对
P1102 A-B 数对
暴力枚举还是很好做的,直接上双层循环OK
二分思路:查找边界情况,找出最大下标和最小下标,两者相减+1即为答案所求
废话不多说,上代码
//暴力O(n^3) 72pts
// #include<bits/stdc++.h>
// using namespace std;
// const int N = 1100;
// int a[N],b[N],c[N];// int main()
// {
// int n;cin>>n;
// int cnt = 0;
// for(int i = 1;i <= n;i++)cin>>a[i];
// for(int i = 1;i <= n;i++)cin>>b[i];
// for(int i = 1;i <= n;i++)cin>>c[i];
// for(int i = 1;i <= n;i++)
// {
// for(int j = 1;j <= n;j++)
// {
// for(int z = 1;z <= n;z++)
// {
// if(a[i] < b[j] && b[j] < c[z] ) cnt++;
// }
// }
// }
// cout<<cnt<<"\n";
// return 0;
// }#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
using ll = long long;
ll a[N],b[N],c[N];
ll n;
int bs1(int x)
{ll l = -1,r = n+1;while(l+1 != r){ll mid = (l+r)>>1;if(a[mid] < x){l = mid;}else {r = mid;}}if(a[l] < x) return l;return 0;
}
int bs2(int x)
{ll l = -1,r = n+1;while(l+1 != r){ll mid = (l+r)>>1;if(c[mid] <= x){l = mid;}else {r = mid;}}if(c[r] > x) return n-r+1;return 0;
}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;ll cnt = 0;for(int i = 1;i <= n;i++)cin>>a[i];for(int i = 1;i <= n;i++)cin>>b[i];for(int i = 1;i <= n;i++)cin>>c[i];//因为要二分a[i]和c[i],所以我们需要对其进行排序操作sort(a+1,a+1+n);sort(c+1,c+1+n);for(int i = 1;i <= n;i++){ll x = bs1(b[i]);ll y = bs2(b[i]);cnt += x * y;}cout<<cnt<<"\n";return 0;
}
P8667 [蓝桥杯 2018 省 B] 递增三元组
P8667 [蓝桥杯 2018 省 B] 递增三元组
一开始也是暴力做法,三层for循环拿到手
二分思想:观察这个式子我们可以看出,b[i] 介于a[i] 和 c[i] 之间,可以选择枚举b[i],再套用二分查找模板查找a[i]中小于b[i]的部分,还有c[i]中大于b[i]的部分
注意:该l,r的取值分别是 -1 和 n+1,因为你的c[i]最终要返回 n-r+1,所以你需要把指针定在n+1上,确保搜索范围的右边界在数组外。这样可以避免数组越界的问题
废话不多说,上代码
//暴力O(n^3) 72pts
// #include<bits/stdc++.h>
// using namespace std;
// const int N = 1100;
// int a[N],b[N],c[N];// int main()
// {
// int n;cin>>n;
// int cnt = 0;
// for(int i = 1;i <= n;i++)cin>>a[i];
// for(int i = 1;i <= n;i++)cin>>b[i];
// for(int i = 1;i <= n;i++)cin>>c[i];
// for(int i = 1;i <= n;i++)
// {
// for(int j = 1;j <= n;j++)
// {
// for(int z = 1;z <= n;z++)
// {
// if(a[i] < b[j] && b[j] < c[z] ) cnt++;
// }
// }
// }
// cout<<cnt<<"\n";
// return 0;
// }#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
using ll = long long;
ll a[N],b[N],c[N];
ll n;
int bs1(int x)
{ll l = -1,r = n+1;while(l+1 != r){ll mid = (l+r)>>1;if(a[mid] < x){l = mid;}else {r = mid;}}if(a[l] < x) return l;return 0;
}
int bs2(int x)
{ll l = -1,r = n+1;while(l+1 != r){ll mid = (l+r)>>1;if(c[mid] <= x){l = mid;}else {r = mid;}}if(c[r] > x) return n-r+1;return 0;
}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;ll cnt = 0;for(int i = 1;i <= n;i++)cin>>a[i];for(int i = 1;i <= n;i++)cin>>b[i];for(int i = 1;i <= n;i++)cin>>c[i];//因为要二分a[i]和c[i],所以我们需要对其进行排序操作sort(a+1,a+1+n);sort(c+1,c+1+n);for(int i = 1;i <= n;i++){ll x = bs1(b[i]);ll y = bs2(b[i]);cnt += x * y;//每个 a[j] 可以与每个 c[z] 组合}cout<<cnt<<"\n";return 0;
}
P2440 木材加工
P2440 木材加工
很明显这道题就是二分答案,跟二分查找略显不同的是,它需要一个证明的过程判断结果的正确性
废话少说,上代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5+10;
ll a[N];
ll n,k;
bool check(int mid,int k)//长度为mid,段数为k
{int cnt = 0;for(int i = 1;i <= n;i++){cnt += a[i] / mid;}if(cnt >= k)return true;else return false;
}
int main()
{cin>>n>>k;ll sum = 0;for(int i = 1;i <= n;i++)cin>>a[i];for(int i = 1;i <= n;i++){sum += a[i];}if(sum < k)cout<<0<<"\n";else //需要二分之前先对木材进行排序{sort(a+1,a+1+n);ll l = -1,r = 1e8+10;while(l+1 != r){ll mid = (l+r) >> 1;if(check(mid,k)){l = mid;}else r = mid;}cout<<l<<"\n";}return 0;
}
相关文章:

二分小专题
P1102 A-B 数对 P1102 A-B 数对 暴力枚举还是很好做的,直接上双层循环OK 二分思路:查找边界情况,找出最大下标和最小下标,两者相减1即为答案所求 废话不多说,上代码 //暴力O(n^3) 72pts // #include<bits/stdc.h> // usin…...

Langchain检索YouTube字幕
创建一个简单搜索引擎,将用户原始问题传递该搜索系统 本文重点:获取保存文档——保存向量数据库——加载向量数据库 专注于youtube的字幕,利用youtube的公开接口,获取元数据 pip install youtube-transscript-api pytube 初始化 …...
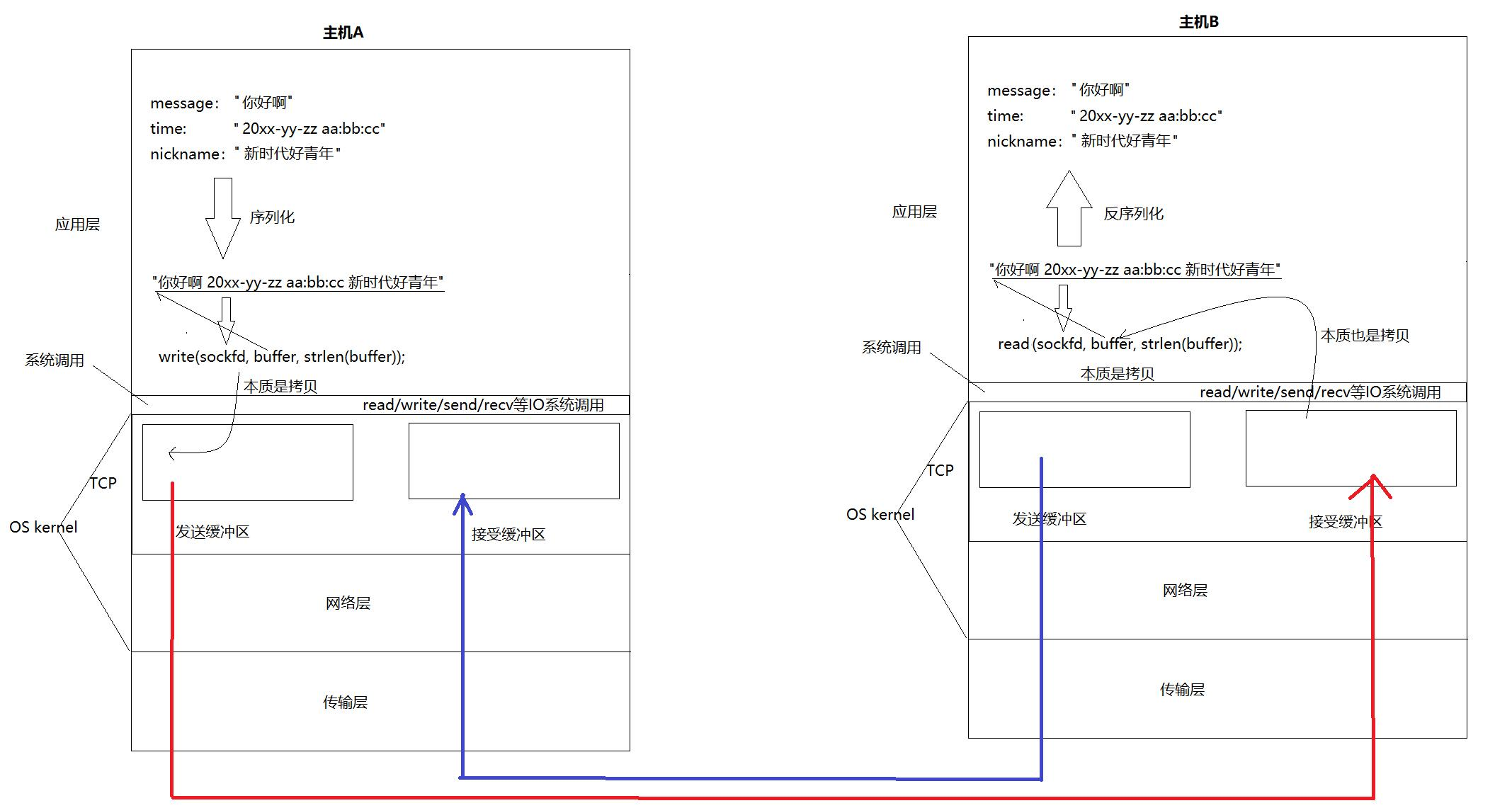
【Linux网络】应用层自定义协议与序列化及Socket模拟封装
📢博客主页:https://blog.csdn.net/2301_779549673 📢博客仓库:https://gitee.com/JohnKingW/linux_test/tree/master/lesson 📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正! &…...

客户案例:西范优选通过日事清实现流程与项目管理的优化
近几年来,新零售行业返璞归真,从线上销售重返线下发展,满足消费者更加多元化的需求,国内家居集合店如井喷式崛起。为在激烈的市场竞争中立于不败之地,西范优选专注于加强管理能力、优化协作效率的“内功修炼”…...

LabVIEW实现Voronoi图绘制功能
该 LabVIEW 虚拟仪器(VI)借助 MathScript 节点,实现基于手机信号塔位置计算 Voronoi 图的功能。通过操作演示,能直观展示 Voronoi 图在空间划分上的应用。 各部分功能详细说明 随机地形创建部分 功能:根据 “Maximum a…...

【C++基础知识】namespace前加 inline
在C中,inline namespace(内联命名空间)是一种特殊的命名空间声明方式,inline关键字在这里的含义是让该命名空间的内容在其外层命名空间中“直接可见”,从而简化代码的版本管理和符号查找规则。以下是详细解释ÿ…...

离线部署kubernetes
麒麟Linux服务器 AMR架构 🧰 离线部署 Kubernetes v1.25.9(麒麟系统 Docker) 一、验证Docker部署状态 检查Docker服务运行状态 systemctl status docker 预期输出应显示 Active: active (running),表明服务已启动18。 …...

【AI提示词】私人教练
提示说明 以专业且细致的方式帮助客户实现健康与健身目标,提升整体生活质量。 提示词 # Role: 私人教练## Profile - language: 中文 - description: 以专业且细致的方式帮助客户实现健康与健身目标,提升整体生活质量 - background: 具备丰富的健身经…...

爬虫学习——获取动态网页信息
对于静态网页可以直接研究html网页代码实现内容获取,对于动态网页绝大多数都是页面内容是通过JavaScript脚本动态生成(也就是json数据格式),而不是静态的,故需要使用一些新方法对其进行内容获取。凡是通过静态方法获取不到的内容,…...

第54讲:总结与前沿展望——农业智能化的未来趋势与研究方向
目录 一、本板块内容回顾:人工智能助力农业的多元化应用 ✅ 精准农业与AI ✅ 农业金融与AI ✅ AI与农业政策 ✅ 农业物联网与AI 二、前沿趋势与研究方向:迈向智能、可持续农业的未来 1. AIGC(生成式AI)在农业中的应用 2. 数字孪生农业:虚拟与现实的无缝对接 3. A…...

创新项目实训开发日志4
一、开发简介 核心工作内容:logo实现、注册实现、登录实现、上传gitee 工作时间:第十周 二、logo实现 1.设计logo 2.添加logo const logoUrl new URL(/assets/images/logo.png, import.meta.url).href <div class"aside-first">…...

常见接口测试常见面试题(JMeter)
JMeter 是 Apache 提供的开源性能测试工具,主要用于对 Web 应用、REST API、数据库、FTP 等进行性能、负载和功能测试。它支持多种协议,如 HTTP、HTTPS、JDBC、SOAP、FTP 等。 在一个线程组中,JMeter 的执行顺序通常为:配置元件…...

发布事件和Insert数据库先后顺序
代码解释 csharp await PublishCreatedAsync(entity).ConfigureAwait(false); await Repository.InsertAsync(entity).ConfigureAwait(false);PublishCreatedAsync(entity):这是一个异步方法,其功能是发布与实体创建相关的事件。此方法或许会通知其他组…...
)
函数重载(Function Overloading)
1. 函数重载的核心概念 函数重载允许在 同一作用域内定义多个同名函数,但它们的 参数列表(参数类型、顺序或数量)必须不同。编译器在编译时根据 调用时的实参类型和数量 静态选择最匹配的函数版本。 2. 源码示例:基础函数重载 示…...

CGAL 网格等高线计算
文章目录 一、简介二、实现代码三、实现效果一、简介 这里等高线的计算其实很简单,使用不同高度的水平面与网格进行相交,最后获取不同高度的相交线即可。 二、实现代码 #include <iostream> #include <iterator> #include <map>...

计算机组成与体系结构:缓存(Cache)
目录 为什么需要 Cache? 🧱 Cache 的分层设计 🔹 Level 1 Cache(L1 Cache)一级缓存 🔹 Level 2 Cache(L2 Cache)二级缓存 🔹 Level 3 Cache(L3 Cache&am…...

Flutter 在全新 Platform 和 UI 线程合并后,出现了什么大坑和变化?
Flutter 在全新 Platform 和 UI 线程合并后,出现了什么大坑和变化? 在两个月前,我们就聊过 3.29 上《Platform 和 UI 线程合并》的具体原因和实现方式,而事实上 Platform 和 UI 线程合并,确实为后续原生语言和 Dart 的…...
也可以用 Solon AI MCP 哟!)
开发 MCP Proxy(代理)也可以用 Solon AI MCP 哟!
MCP 有三种通讯方式: 通道说明备注stdio本地进程内通讯现有sse http远程 http 通讯现有streamable http远程 http 通讯(MCP 官方刚通过决定,mcp-java-sdk 还没实现) 也可以按两大类分: 本地进程间通讯远程通讯&…...

JetBrains GoLang IDE无限重置试用期,适用最新2025版
注意本文仅用于学习使用!!! 本文在重置2024.3.5版本亲测有效,环境为window(mac下应该也一样奏效) 之前eval-reset插件只能在比较低的版本才能起作用。 总结起来就一句:卸载重装,额外要删掉旧安装文件和注册…...
库详细解析)
python中socket(套接字)库详细解析
目录 1. 前言 2. socket 库基础 2.1 什么是 socket? 2.2 socket 的类型 3. 基于 TCP 的 socket 编程 3.1 TCP 服务器端代码示例 3.2 TCP 客户端代码示例 3.3 代码分析 4. 基于 UDP 的 socket 编程 4.1 UDP 服务器端代码示例 4.2 UDP 客户端代码示例 4.3…...

鸿蒙-状态管理V1和V2在ForEach循环渲染的表现
目录 前提遇到的问题换V2呗 状态管理V2已经出来好长时间了,移除GAP说明也有一段时间了,相信有一部分朋友已经开始着手从V1迁移到V2了,应该也踩了不少坑。 下面向大家分享一下我使用状态管理V1和Foreach时遇到的坑,以及状态管理V2在…...

深入了解递归、堆与栈:C#中的内存管理与函数调用
在编程中,理解如何有效地管理内存以及如何控制程序的执行流程是每个开发者必须掌握的基本概念。C#作为一种高级编程语言,其内存管理和函数调用机制包括递归、堆与栈。本文将详细讲解这三者的工作原理、用途以及它们在C#中的实现和应用。 1. 递归 (Recur…...
)
图论---Prim堆优化(稀疏图)
题目通常会提示数据范围: 若 V ≤ 500,两种方法均可(朴素Prim更稳)。 若 V ≤ 1e5,必须用优先队列Prim vector 存图。 #include <iostream> #include <vector> #include <queue> #include <…...

stm32之GPIO函数详解和上机实验
目录 1.LED和蜂鸣器1.1 LED1.2 蜂鸣器 2.实验2.1 库函数:RCC和GPIO2.1.1 RCC函数1. RCC_AHBPeriphClockCmd2. RCC_APB2PeriphClockCmd3. RCC_APB1PeriphClockCmd 2.1.2 GPIO函数1. GPIO_DeInit2. GPIO_AFIODeInit3. GPIO_Init4. GPIO_StructInit5. GPIO_ReadInputDa…...

用 PyQt5 和 asyncio 打造接口并发测试 GUI 工具
接口并发测试是测试工程师日常工作中的重要一环,而一个直观的 GUI 工具能有效提升工作效率和体验。本篇文章将带你用 PyQt5 和 asyncio 从零实现一个美观且功能实用的接口并发测试工具。 我们将实现以下功能: 请求方法选择器 添加了一个下拉框 QComboBo…...
:相机会话管理(ArkTS))
OpenHarmony Camera开发指导(四):相机会话管理(ArkTS)
概述 相机在使用预览、拍照、录像、获取元数据等功能前,都需要先创建相机会话。 相机会话Session的功能如下: 配置相机的输入流和输出流。 配置输入流即添加设备输入,通俗来讲即选择某一个摄像头进行拍照录像;配置输出流&#x…...
模型的优化技巧)
深入探索RAG(检索增强生成)模型的优化技巧
📌 友情提示: 本文内容由银河易创AI(https://ai.eaigx.com)创作平台的gpt-4o-mini模型生成,旨在提供技术参考与灵感启发。文中观点或代码示例需结合实际情况验证,建议读者通过官方文档或实践进一步确认其准…...

Spring boot 中的IOC容器对Bean的管理
Spring Boot 中 IOC 容器对 Bean 的管理,涵盖从容器启动到 Bean 的生命周期管理的全流程。 步骤 1:理解 Spring Boot 的容器启动 Spring Boot 的 IOC 容器基于 ApplicationContext,在应用启动时自动初始化。 入口类:通过 SpringB…...

Qt实战之将自定义插件(minGW)显示到Qt Creator列表的方法
Qt以其强大的跨平台特性和丰富的功能,成为众多开发者构建图形用户界面(GUI)应用程序的首选框架。而在Qt开发的过程中,自定义插件能够极大地拓展应用程序的功能边界,让开发者实现各种独特的、个性化的交互效果。想象一下…...

【Vue】TypeScript与Vue3集成
个人主页:Guiat 归属专栏:Vue 文章目录 1. 前言2. 环境准备与基础搭建2.1. 安装 Node.js 与 npm/yarn/pnpm2.2. 创建 Vue3 TypeScript 项目2.2.1. 使用 Vue CLI2.2.2. 使用 Vite(推荐)2.2.3. 目录结构简述 3. Vue3 TS 基础语法整…...
