数据结构——二叉树,堆
目录
1.树
1.1树的概念
1.2树的结构
2.二叉树
2.1二叉树的概念
2.2特殊的二叉树
2.3二叉树的性质
2.4二叉树的存储结构
2.4.1顺序结构
2.4.2链式结构
3.堆
3.1堆的概念
3.2堆的分类
3.3堆的实现
3.3.1初始化
3.3.2堆的构建
3.3.3堆的销毁
3.3.4堆的插入
3.3.5堆的删除
3.3.6取堆顶的数据
3.3.7堆的数据个数
3.3.8堆的判空
3.4堆排序
3.5 TOP-K问题
4.二叉树链式结构的实现
4.1二叉树结构
4.2二叉树遍历
4.2.1前序遍历
4.2.2中序遍历
4.2.3后序遍历
4.2.4层序遍历
4.3基础接口实现
4.3.1二叉树结点个数
4.3.2二叉树的高度
4.3.3 二叉树叶子结点个数
4.3.4 二叉树第k层结点个数
4.3.5 二叉树查找值为x的结点
4.3.6 通过前序遍历的数组构建二叉树
4.3.7 二叉树销毁
4.3.8 判断二叉树是否是完全二叉树
1.树
1.1树的概念

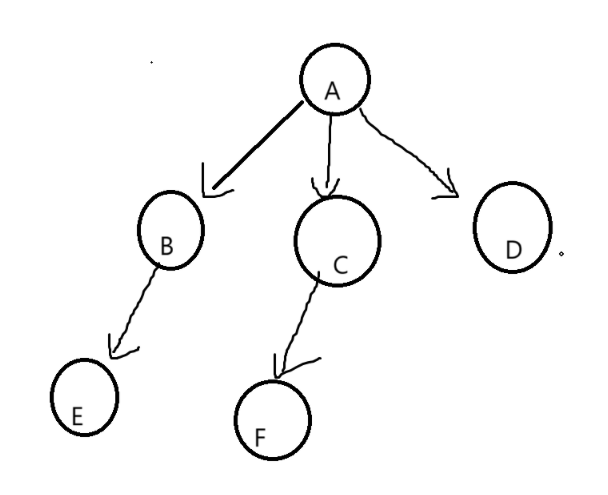
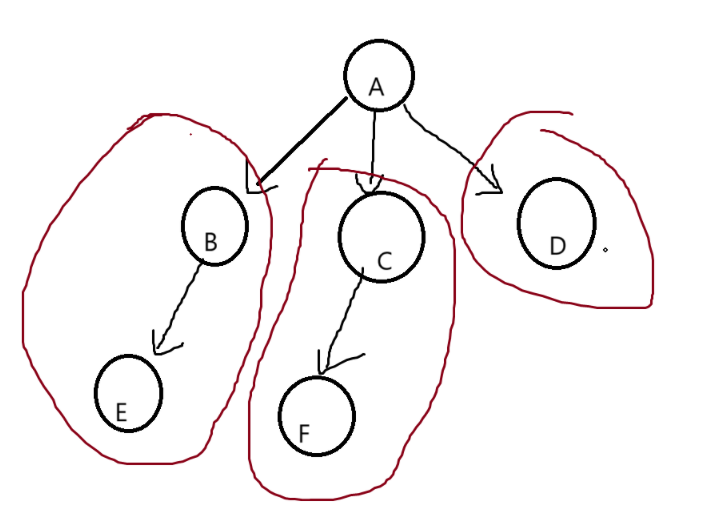
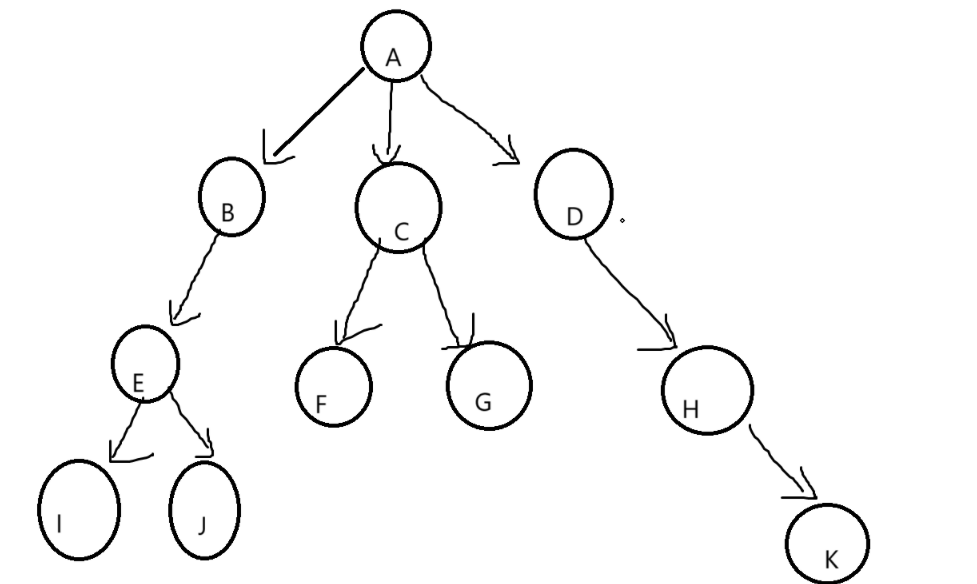
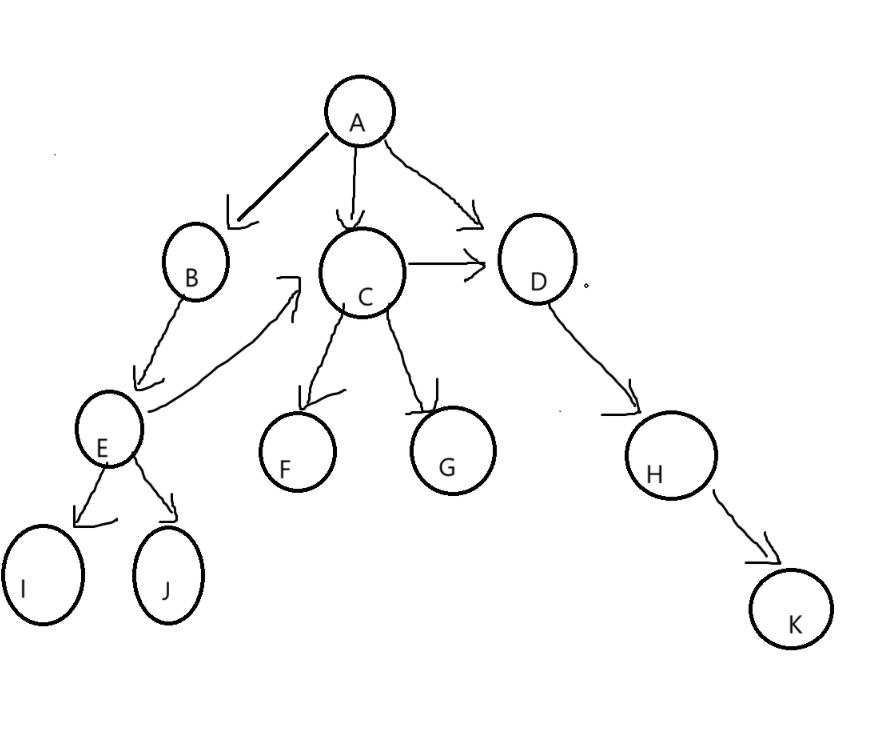
1.2树的结构
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一个孩子结点struct Node* pNextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域
};2.二叉树
2.1二叉树的概念
树的度为2的树,可以为空,也可以只有一个(根)节点,只有左右子树和节点
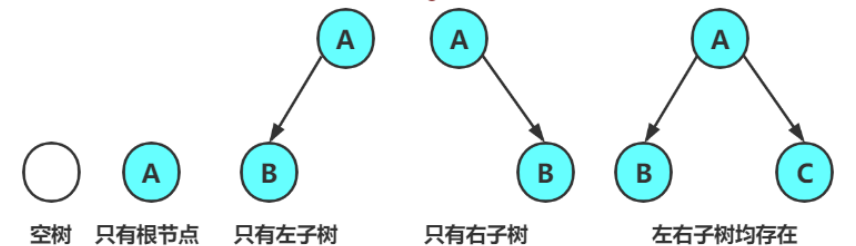
2.2特殊的二叉树
2.3二叉树的性质
1. 若规定根结点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有 2 *(i-1)个结点(*代表次方)2. 若规定根结点的层数为 1 ,则 深度为 h的二叉树的最大结点数是 2*h-1(*代表次方)3. 对任何一棵二叉树 , 如果度为 0 其叶结点个数为 , 度为 2 的分支结点个数为 , 则有 = + 14. 若规定根结点的层数为 1 ,具有 n 个结点的满二叉树的深度 , h=log(n+1)(ps :是log 以 2为底,n+1 为对数 )5. 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有结点从 0 开始编号,则对于序号为i 的结点有:1. 若 i>0 , i 位置结点的双亲序号: (i-1)/2 ; i=0 , i 为根结点编号,无双亲结点2. 若 2i+1<n ,左孩子序号: 2i+1 , 2i+1>=n 否则无左孩子3. 若 2i+2<n ,右孩子序号: 2i+2 , 2i+2>=n 否则无右孩子
2.4二叉树的存储结构
2.4.1顺序结构
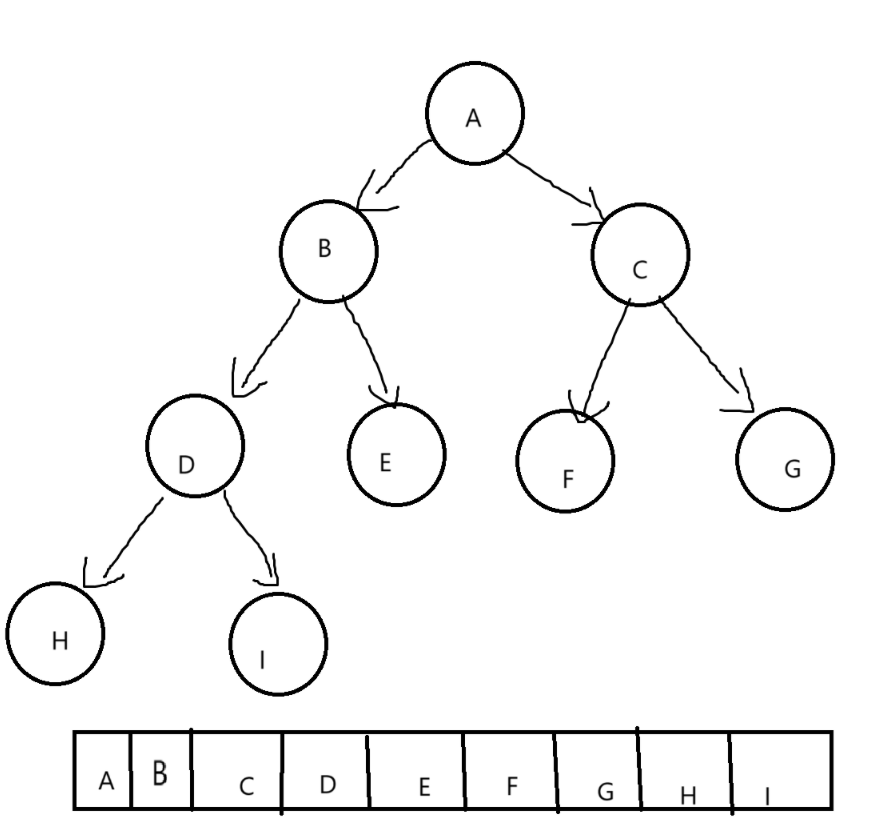
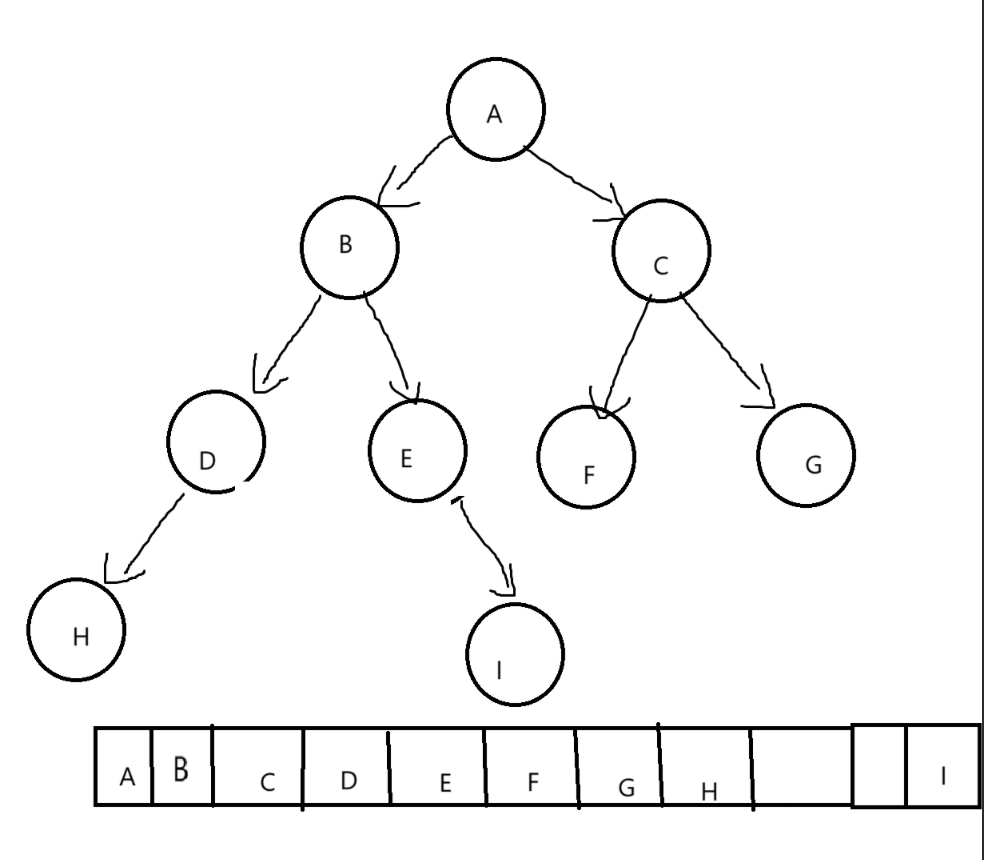
2.4.2链式结构
typedef int BTDataType;
// 二叉链
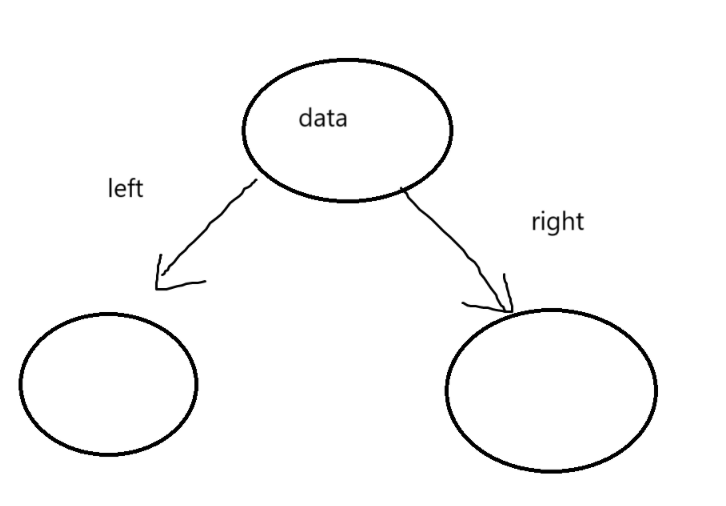
struct BinaryTreeNode
{struct BinTreeNode* left; // 指向当前结点左孩子struct BinTreeNode* right; // 指向当前结点右孩子BTDataType data; // 当前结点值域
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* parent; // 指向当前结点的双亲struct BinTreeNode* left; // 指向当前结点左孩子struct BinTreeNode* right; // 指向当前结点右孩子int data; // 当前结点值域
};3.堆
3.1堆的概念
就是一种二叉树,储存的方式是数组
3.2堆的分类
完全二叉树用数组存储堆有两种类型一种是小跟堆,一种是大根堆
小跟堆:任何一个父节点<=子节点
逻辑

存储

大根堆:任何一个父节点>=子节点
逻辑

存储

3.3堆的实现
创建文件不再叙述
3.3.1初始化
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;3.3.2堆的构建
void HeapCreate(Heap* hp)
{assert(hp);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}3.3.3堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}3.3.4堆的插入
当插入一个数据时,此时可能不符合小堆(大堆),因此插入一个数据化,要对数据进行调整,此时我们就要用到向上调整算法
用小堆举例
当我们数据插入到最后一位时,根据小堆性质(任何一个父节点<=子节点)与当前节点的父节点比较,如果父节点>子节点,交换数据,如此重复,直到父节点<=子节点,或者子节点在数组的位置<=0跳出;
//向上调整
void AdjustUp(HPDataType* HP, int child)
{int parent = (child - 1) / 2;//找到父节点while (child > 0){if (HP[parent] > HP[child])//建小堆,父节点<=子节点{swap(&HP[parent], &HP[child]);child = parent;parent = (child - 1) / 2;}//if (HP[parent] < HP[child])//建大堆,父节点>=子节点//{// swap(&HP[parent], &HP[child]);// child = parent;// parent = (child - 1) / 2;//}else{break;}}
}
//交换数据
void swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);//扩容if (hp->_capacity == hp->_size){int tmp = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;HPDataType* new = (HPDataType*)ralloc(hp->_a, 2 * sizeof(HPDataType));if (new == NULL){perror("new");return;}hp->_capacity = tmp;hp->_a = new;}hp->_a[hp->_size++] = x;向上调整AdjustUp(hp->_a, hp->_size - 1);//第一个参数的数组指针,第二个参数是x在数组的位置
}3.3.5堆的删除
对于堆的删除,我们不是删除堆的最后一个元素,而是删除堆顶的数据,也就是根节点的数据,对于根节点数据的删除,我们不能直接把数组的一个数据覆盖(根节点的数据)


我们发现直接覆盖根节点,父子关系就会混乱,同时小堆(大堆)的特性也会消失
这里,我们就可以用到,向下调整算法
同样用小堆举例
当删除数据之前,先把堆顶元素与最后一个元素交换,之后删除最后一个元素,对堆顶数据进行向下调整,当数据交换后,根据小堆性质(任何一个父节点<=子节点),先判断左右子节点那个小,与较小的子节点比较,如果父节点>子节点,交换数据,如此重复,直到父节点数据<=子节点数据,或者子节点在数组的位置>=n(数组内有效数组个数后一位)跳出;

void AdjustDown(HPDataType* HP, int n,int parent)
{//假设左孩子小int child = parent * 2 + 1;while (child < n){if (child+1<n && HP[child] > HP[child + 1]){child++;}if (HP[child] < HP[parent]){swap(&HP[child], &HP[parent]);parent = child;child = parent * 2 + 1;}//假设左孩子大//if (child + 1 < n && HP[child] > HP[child + 1])//大堆//{// child++;//}//if (HP[child] > HP[parent])//{// swap(&HP[child], &HP[parent]);// parent = child;// child = parent * 2 + 1;//}else{break;}}
}
void HeapPop(Heap* hp)
{assert(hp);assert(hp->_size > 0);Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;AdjustDown(hp->_a, hp->_size, 0);
}其实这里有点有排序的意味,当我们每次pop都是堆里最小的元素,当pop完整个数组,对于小堆,就可以获取一份从小到大的数据,但是这里并不是排序,这里我们只是打印排序,并没有把数组中的元素排序
3.3.6取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(hp->_size > 0);return hp->_a[0];
}3.3.7堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}3.3.8堆的判空
// 堆的判空
int HeapEmpty(Heap* hp)
{return hp->_size == 0;
}3.4堆排序
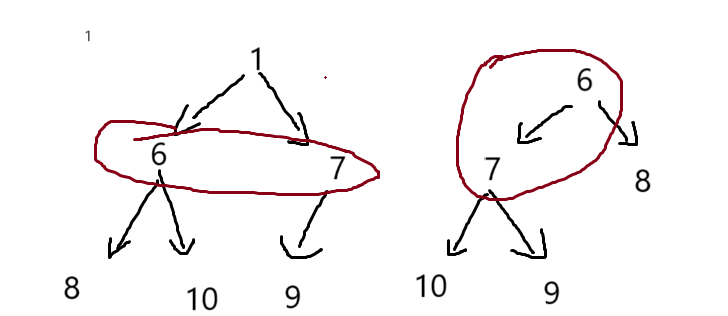
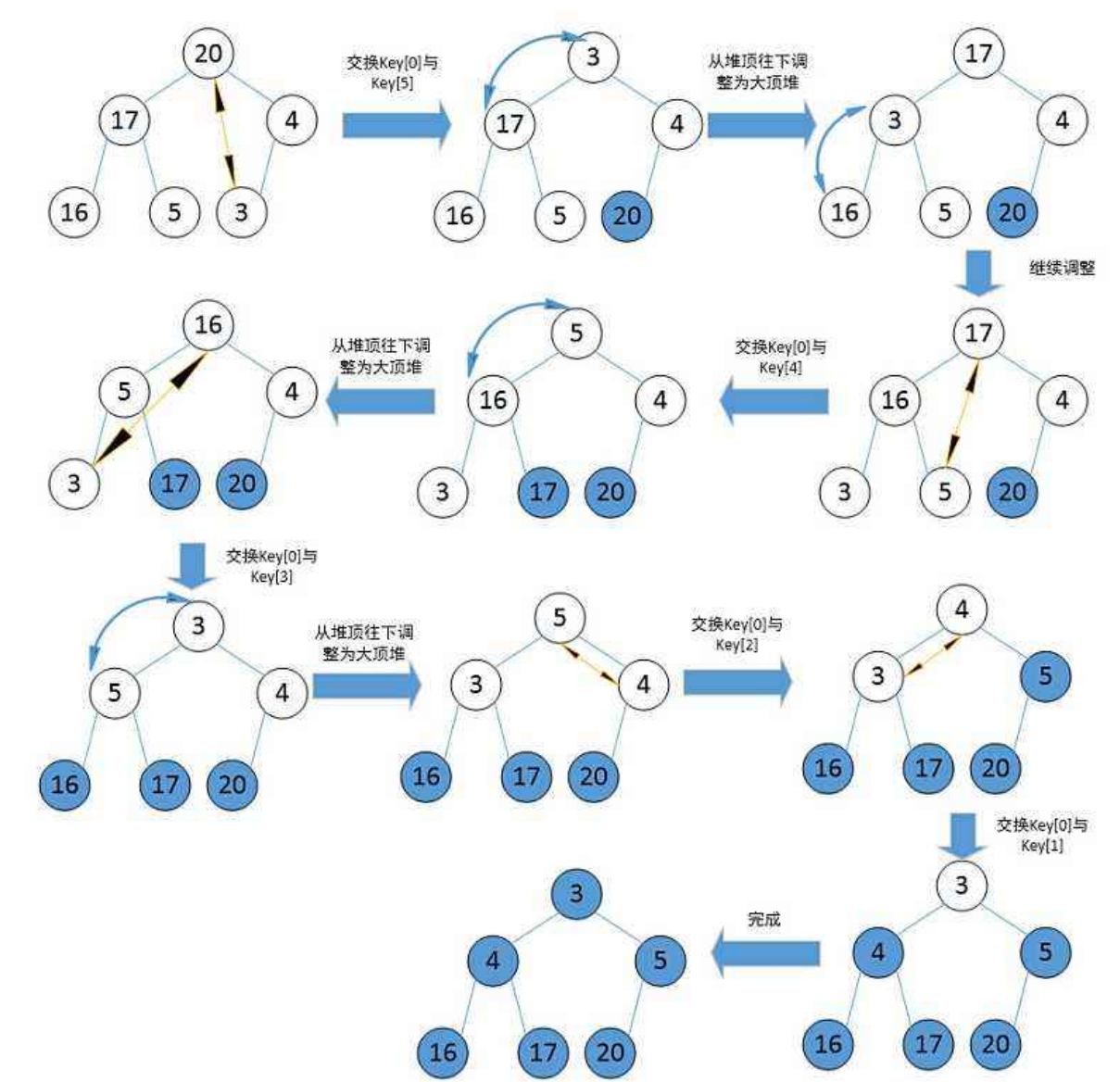
void HeapSort()
{int a[] = { 4,8,1,5,6,9,7,3,2};Heap hp;//升序建大堆//降序建小堆int n = sizeof(a) / sizeof(int);for (int i = 0; i <n; i++){AdjustUp(a, i);}int end = n-1;//最后一个元素的位置while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}![]()
对于向上调整建堆,它的时间复杂度是O(N*logN)
当我们用向下调整算法建堆时,时间复杂度为O(N)(此文章不做证明,有兴趣可以去查询)
void HeapSort()
{int a[] = { 4,8,1,5,6,9,7,3,2};Heap hp;//升序建大堆//降序建小堆int n = sizeof(a) / sizeof(int);int end = n-1;//最后一个元素的位置for (int i = (end - 1) / 2; i >= 0; i--)//(end - 1) / 2求父亲节点{AdjustDown(a, i, 0);}while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}3.5 TOP-K问题
前 k 个最大的元素,则建小堆前 k 个最小的元素,则建大堆
//创建数据
void CreateNDate()
{// 造数据int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}
void TestHeap()
{int k;printf("请输入k>:");scanf("%d", &k);int* kminheap = (int*)malloc(sizeof(int) * k);if (kminheap == NULL){perror("malloc fail");return;}const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");return;}// 读取文件中前k个数for (int i = 0; i < k; i++){fscanf(fout, "%d", &kminheap[i]);}// 建K个数的小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(kminheap, k, i);}// 读取剩下的N-K个数int x = 0;while (fscanf(fout, "%d", &x) > 0)//读取文件剩下的数据{if (x > kminheap[0]){kminheap[0] = x;AdjustDown(kminheap, k, 0);}}printf("最大前%d个数:", k);for (int i = 0; i < k; i++){printf("%d ", kminheap[i]);}printf("\n");
}int main()
{//创建数据CreateNDate();TestHeap();return 0;
}如何确定这前k个数是最大的,在创建数据时可以模上一个数,int x = (rand() + i) % 10000000;
就像这样,代表随机出来的数不可能超过10000000,之后我们可以在文件中改变几个数据,让这几个数据大于10000000,然后运行程序,看看前k个数是否为你改的几个数。
4.二叉树链式结构的实现
4.1二叉树结构
1. 空树2. 非空:根结点,根结点的左子树、根结点的右子树组成的。
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->_data = x;node->_left = NULL;node->_right = NULL;return node;
}
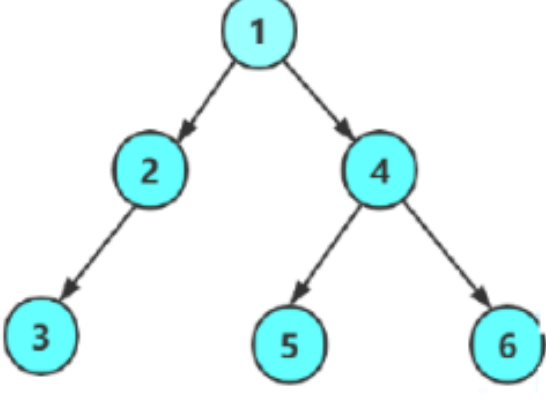
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;node1->_right = node4;node2->_left = node3;node4->_left = node5;node4->_right = node6;return node1;
}
4.2二叉树遍历
1. 前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点的操作发生在遍历其左右子树之前。2. 中序遍历 (Inorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之中(间)。3. 后序遍历 (Postorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之后。
4.2.1前序遍历
根 左子树 右子树


void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->_data);PrevOrder(root->_left);PrevOrder(root->_right);
}4.2.2中序遍历
左子树 根 右子树

void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->_left);printf("%d ", root->_data);InOrder(root->_right);
}4.2.3后序遍历
左子树 右子树 根

void Postorde(BTNode* root)
{if (root == NULL){printf("N ");return;}Postorde(root->_left);Postorde(root->_right);printf("%d ", root->_data);
}4.2.4层序遍历
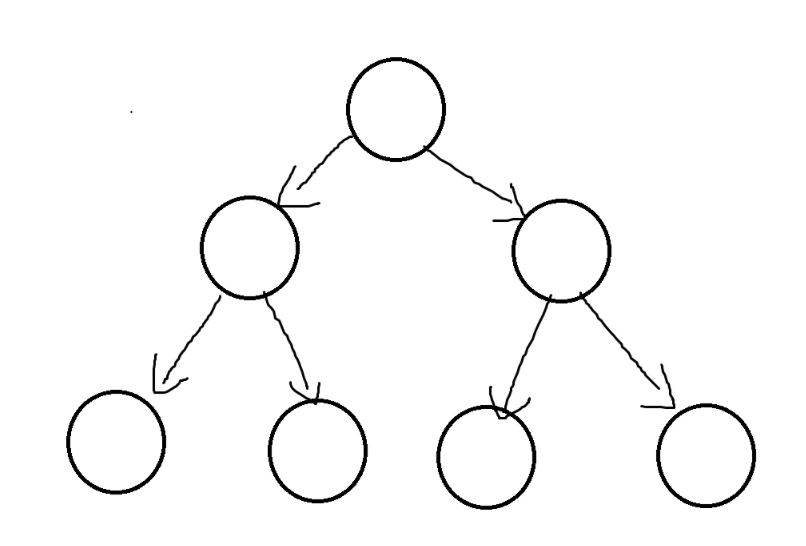
每层每层遍历


遍历的结果就是1,2,3,4,5,6,而这种遍历则需要用到队列来实现,当把1放进队列,把1的左右节点放进队列,把1丢出,再把2和4的左右节点放进队列,把2,4丢出,重复如此,就完成了层序遍历
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//初始化队列if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->_data);if (front->_left){QueuePush(&q,front->_left);}if (front->_right){QueuePush(&q, front->_right);}}QueueDestroy(&q);//队列销毁
}4.3基础接口实现
4.3.1二叉树结点个数
int size = 0;
int TreeSize(BTNode* root)
{if (root == NULL)return 0;else++size;TreeSize(root->_left);TreeSize(root->_right);return size;
}对于这个程序,每次我们调用都要使size=0,我们可以优化一下
int TreeSize(BTNode* root)
{return root == NULL ? 0 :TreeSize(root->_left) + TreeSize(root->_right) + 1;
}这个就相当于左子树的节点+右子树的节点+1(自己本身)
4.3.2二叉树的高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return TreeHeight(root->left) > TreeHeight(root->right) ?TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}这个程序有一些效率问题,每次判断完后,还要进入递归,导致重复计算很多,效率很低,因此可以用一个变量来存储
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->_left);int rightHeight = TreeHeight(root->_right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}4.3.3 二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL)//判断是否是叶子节点{return 1;}return BinaryTreeLeafSize(root->_left)+BinaryTreeLeafSize(root->_right);//递归左右子树}4.3.4 二叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)//根节点为第一层
{if (k == 1){return 1;}if (root == NULL){return 0;}return BinaryTreeLevelKSize(root->_left, k - 1) +BinaryTreeLevelKSize(root->_right, k - 1);//递归左右子树
}4.3.5 二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root->_data == x){return root;}BTNode* ret = BinaryTreeFind(root->_left, x);//存储结果if (ret)//当查到就返回{return ret;}return BinaryTreeFind(root->_right, x);
}4.3.6 通过前序遍历的数组构建二叉树
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(char* a, int n, int* pi)//char*a代表要构建的数据 n代表a内的数据个数
{if (a[*pi] == '#'){(*pi)++;return NULL;}if (n == *pi){return NULL;}BTNode* ret = (BTNode*)malloc(sizeof(BTNode));ret->_data = a[(*pi)++];ret->_left = BinaryTreeCreate(a,n,pi);ret->_right = BinaryTreeCreate(a,n,pi);return ret;
}4.3.7 二叉树销毁
对于二叉树的销毁,要选择后序遍历,如果选择前中序遍历销毁,就无法找到所有节点
void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;TreeDestory(root->_left);TreeDestory(root->_right);free(root);
}4.3.8 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}if (front->_left){QueuePush(&q, front->_left);}if (front->_right){QueuePush(&q, front->_right);}}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 如果有非空,就不是完全二叉树if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}相关文章:

数据结构——二叉树,堆
目录 1.树 1.1树的概念 1.2树的结构 2.二叉树 2.1二叉树的概念 2.2特殊的二叉树 2.3二叉树的性质 2.4二叉树的存储结构 2.4.1顺序结构 2.4.2链式结构 3.堆 3.1堆的概念 3.2堆的分类 3.3堆的实现 3.3.1初始化 3.3.2堆的构建 3.3.3堆的销毁 3.3.4堆的插入 3.3.5…...

Java面试实战:音视频场景下的微服务架构与缓存技术剖析
文章标题 Java面试实战:音视频场景下的微服务架构与缓存技术剖析 文章内容 第一轮提问 面试官: 谢先生,请问您对Spring Boot框架熟悉吗?它有哪些核心特性? 谢飞机: 熟悉,Spring Boot的核心特性包括自动配置、嵌入…...

龙虎榜——20250424
指数依然是震荡走势,接下来两天调整的概率较大 2025年4月24日龙虎榜行业方向分析 一、核心主线方向 化工(新能源材料产能集中) • 代表标的:红宝丽(环氧丙烷/锂电材料)、中欣氟材(氟化工&…...

大学生如何学好人工智能
大学生学好人工智能需要从多个方面入手,以下是一些建议: 扎实掌握基础知识 - 数学基础:人工智能涉及大量数学知识,要学好线性代数、概率论、数理统计、微积分等课程,为理解复杂的算法和模型奠定基础。 - 编程语言&…...

实时步数统计系统 kafka + spark +redis
基于微服务架构设计并实现了一个实时步数统计系统,采用生产者-消费者模式,利用Kafka实现消息队列,Spark Streaming处理实时数据流,Redis提供高性能数据存储,实现了一个高并发、低延迟的数据处理系统,支持多…...
CentOS 7 安装教程
准备: 软件:VMware Workstation 镜像文件:CentOS-7-x86_64-bin-DVD1.iso (附:教程较为详细,注释较多,故将操作的选项进行了加粗字体显示。) 1、文件–新建虚拟机–自定义 2、硬盘…...

Python+AI提示词出租车出行轨迹预测:梯度提升GBR、KNN、LR回归、随机森林融合及贝叶斯概率异常检测研究
原文链接:tecdat.cn/?p41693 在当今数字化浪潮席卷全球的时代,城市交通领域的海量数据如同蕴藏着无限价值的宝藏等待挖掘。作为数据科学家,我们肩负着从复杂数据中提取关键信息、构建有效模型以助力决策的使命(点击文末“阅读原文…...

直接偏好优化(Direct Preference Optimization,DPO):论文与源码解析
简介 虽然大规模无监督语言模型(LMs)学习了广泛的世界知识和一些推理技能,但由于它们是基于完全无监督训练,仍很难控制其行为。 微调无监督LM使其对齐偏好,尽管大规模无监督的语言模型(LMs)能…...

2025/4/23 心得
第一题。 习题2.1.9 最少翻转次数 题目描述 给定一个01序列,小x每次可以翻转一个元素,即将该元素从0变1或者从1变0。 现在小x希望最终序列是不下降序列,即不会存在相邻两个元素,左边元素的值比右边元素的值大。 请你帮小x求最…...

dmncdm达梦新云缓存数据库主从集群安装部署详细步骤说明
dmncdm达梦新云缓存数据库主从集群安装部署详细步骤说明 1 环境介绍2 安装部署dmncdm2.1 196部署cdm环境2.2 197部署cdm环境2.3 190部署cdm环境 3 主备集群/主从集群配置4 部署主备集群/主从集群5 部署日志6 更多达梦数据库全方位指南:安装 优化 与实战教程 1 环境介绍 cpu x8…...

UE5.2+VarjoXR3,Lumen、GI、Nanite无效的两种解决方案
一、问题描述 最近在做一个基于VarjoXR3的VR项目开发,UE版本使用的是5.2,效果采用Lumen。首先在PC版本中调整了一个效果,但是当切换到VR运行后,就发现Lumen效果就丢失了。但是测试的其他的头显就没有问题,比如Quest。…...

PH热榜 | 2025-04-24
1. Peek 标语:AI个人财务教练,帮你做出明智的财务决策。 介绍:Peek的人工智能助手能够主动进行财务检查,分析你的消费模式,并以一种细腻而积极的方式帮助你改善习惯。完全没有评判,也没有负罪感。就像为你…...

利用 SSE 实现文字吐字效果:技术与实践
利用 SSE 实现文字吐字效果:技术与实践 引言 在现代 Web 应用开发中,实时交互功能愈发重要。例如,在线聊天、实时数据监控、游戏中的实时更新等场景,都需要服务器能够及时将数据推送给客户端。传统的请求 - 响应模式在处理实时性要求较高的场景时显得力不从心,而 Server…...

POSIX多线程
在计算机编程的广阔领域中,POSIX 标准就像是一把通用的钥匙,开启了跨平台编程的大门。POSIX,即 Portable Operating System Interface(可移植操作系统接口) ,是 IEEE 为了规范各种 UNIX 操作系统提供的 API…...

济南国网数字化培训班学习笔记-第二组-1节-输电线路工程
输电线路工程 输电 电网定义 将发电场采集的电能通过输电线路传输到用户终端。由输电线路、变电站和配电网络等组成。 六精四化 安全、质量、进度、造价、技术、队伍 标准化,模块化,机械化,智能化 发展历程 1908-22kv-石龙坝水电-昆明…...

相机雷达外参标定算法调研
0. 简介 相机与激光雷达的外参标定是自动驾驶、机器人等领域的基础工作。精准的标定不仅有助于提高数据融合的效果,还能提升算法的整体性能。随着技术的发展,许多研究者和公司致力于开发高效的标定工具和算法,本文将对无目标标定和有目标标定…...

网络原理 - 7(TCP - 4)
目录 6. 拥塞控制 7. 延时应答 8. 捎带应答 9. 面向字节流 10. 异常情况 总结: 6. 拥塞控制 虽然 TCP 有了滑动窗口这个大杀器,就能够高效可靠的发送大量的数据,但是如果在刚开始阶段就发送大量的数据,仍然可能引起大量的…...
)
JAVA---面向对象(上)
今天写重生之我开始补知识 第二集 面向对象编程:拿东西过来做对应的事。 设计对象并使用 1.类和对象 类(设计图):是对象共同特征的描述; 对象:是具体存在的具体东西; 如何定义类…...

idea连接远程服务器kafka
一、idea插件安装 首先idea插件市场搜索“kafka”进行插件安装 二、kafka链接配置 1、检查服务器kafka配置 配置链接前需要保证远程服务器的kafka配置里边有配置好服务器IP,以及开放好kafka端口9092(如果有修改 过端口的开放对应端口就好) …...

Linux操作系统--基础I/O(上)
目录 1.回顾C文件接口 stdin、stdout、stderr 2.系统文件I/O 3.接口介绍 4.open函数返回值 5.文件描述符fd 5.1 0&1&2 1.回顾C文件接口 hello.c写文件 #include<stdio.h> #include<string.h>int main() {FILE *fp fopen("myfile","…...

IOMUXC_SetPinMux的0,1参数解释
IOMUXC_SetPinMux(IOMUXC_ENET1_RX_DATA0_FLEXCAN1_TX, 0); 这里的第二个参数 0 实际上传递给了 inputOnfield,它控制的是 SION(Software Input On)位。 当 inputOnfield 为 0 时,SION 关闭,此时引脚的输入/输出方向由…...

go 的 net 包
目录 一、net包的基本功能 1.1 IP地址处理 1.2 网络协议支持 1.3 连接管理 二、net包的主要功能模块 2.1 IP地址处理 2.2 TCP协议 2.3 UDP协议 2.4 Listener和Conn接口 三、高级功能 3.1 超时设置 3.2 KeepAlive控制 3.3 获取连接信息 四、实际应用场景 4.1 Web服…...

weibo_har鸿蒙微博分享,单例二次封装,鸿蒙微博,微博登录
weibo_har鸿蒙微博分享,单例二次封装,鸿蒙微博 HarmonyOS 5.0.3 Beta2 SDK,原样包含OpenHarmony SDK Ohos_sdk_public 5.0.3.131 (API Version 15 Beta2) 🏆简介 zyl/weibo_har是微博封装使用,支持原生core使用 &a…...

【MySQL数据库入门到精通-06 DCL操作】
一、DCL DCL英文全称是Data Control Language(数据控制语言),用来管理数据库用户、控制数据库的访 问权限。 二、管理用户 1.查询与创建用户 代码如下(示例): -- DCL 管理用户 -- 1.查询用户 use mysql; select *from user;-…...

第55讲:农业人工智能的跨学科融合与社会影响——构建更加可持续、包容的农业社会
目录 一、农业人工智能的多维融合:科技与社会的桥梁 1. 技术与社会:解决现代农业中的不平等 2. AI与伦理:塑造道德规范与社会责任 3. AI与政策:推动农业政策的科学决策与智能执行 二、AI与农业未来社会的构建:更绿色、更智能、更包容 1. 推动农业可持续发展:绿色农…...

nodejs之Express-介绍、路由
五、Express 1、express 介绍 express 是一个基于 Node.js 平台的极简、灵活的 WEB 应用开发框架,官方网址: https://www.expressjs.com.cn/ 简单来说,express 是一个封装好的工具包,封装了很多功能,便于我们开发 WEB 应用(HTTP 服务) (1)基本使用 第一步:初始化项目并…...

无感字符编码原址转换术——系统内存(Mermaid文本图表版/DeepSeek)
安全便捷无依赖,不学就会无感觉。 笔记模板由python脚本于2025-04-24 20:00:05创建,本篇笔记适合正在研究字符串编码制式的coder翻阅。 学习的细节是欢悦的历程 博客的核心价值:在于输出思考与经验,而不仅仅是知识的简单复述。 P…...

ecovadis认证需要提供哪些文件?ecovadis认证优势是什么?
EcoVadis认证详解:所需文件与核心优势 一、EcoVadis认证需要提供哪些文件? EcoVadis评估基于企业提交的ESG(环境、社会、治理)相关文档,具体包括以下四类核心主题的文件: 1. 环境(Environment…...

第七部分:向量数据库和索引策略
什么是矢量数据库? 简单来说,向量数据库是一种专门化的数据库,旨在优化存储和检索以高维向量形式表示的文本。 为什么这些数据库对RAG至关重要?因为向量表示能够在大规模文档库中进行高效的基于相似性的搜索,根据用户…...

Java 2025 技术全景与实战指南:从新特性到架构革新
作为一名Java开发者,2025年的技术浪潮将带给我们前所未有的机遇与挑战。本文将带你深入探索Java生态的最新发展,从语言特性到架构革新,助你在技术洪流中把握先机! 🌟 Java 2025 新特性全景 1. 模式匹配的全面进化 (J…...
