2025年GPLT团体程序设计天梯赛L1-L2
目录
1.珍惜生命
2.偷感好重
3.高温补贴
4.零头就抹了吧
5.这是字符串题
6.这不是字符串题
7.大幂数编辑
8.现代战争编辑
9.算式拆解
10.三点共线
11.胖达的山头
12.被n整除的n位数
1.珍惜生命

【解析】直接输出即可
#include<bits/stdc++.h>
using namespace std;
int main(){cout<<"Always code as if the guy who ends up maintaining your code will be a violent psychopath who knows where you live.";
} 2.偷感好重

【解析】直接将三个数相加即可
#include<bits/stdc++.h>
using namespace std;
int main(){
int a,b,c;
cin>>a>>b>>c;
int sum=a+b+c;
cout<<sum;
}3.高温补贴

【解析】这题才开始正向根据题意即先考虑是否补贴的话题意可能有些不清楚,那我们逆着想不补贴的情况写了,剩下的就是补贴的了。
#include<bits/stdc++.h>
using namespace std;
int main(){int T,s,t;cin>>T>>s>>t;int f=0;if((T>35&&t>=33)&&!s){
cout<<"Shi Nei"<<endl;
cout<<T; }else if(s&&(T<=35||t<33)){cout<<"Bu Re"<<endl;cout<<t;}else if((T<=35||t<33)&&!s){cout<<"Shu Shi"<<endl;cout<<t;}else{cout<<"Bu Tie"<<endl;cout<<T;}}4.零头就抹了吧

【解析】 二进制取整
#include<bits/stdc++.h>
using namespace std;
int n;
vector<int> a;
int main(){cin>>n;while(n){a.push_back(n>>1);n>>=1;
}
int k=1;
for(int i=0;i<a.size()-1;i++){k<<=1;
}
cout<<k;
}5.这是字符串题

【解析】数组模拟
#include<bits/stdc++.h>
using namespace std;
string s;
int a[27],b[27];
long long sum=0;
int main(){
cin>>s;
memset(b,0,sizeof(b));
for(int i=0;i<26;i++){cin>>a[i];
}
for(int i=0;i<s.size();i++){sum+=a[s[i]-'a'];b[s[i]-'a']++;
}
for(int i=0;i<26;i++){cout<<b[i];if(i!=25)cout<<" ";
}
cout<<endl;
cout<<sum;
} 6.这不是字符串题

【解析】哇,这个不是字符串题比不是字符串题要难得多啊,我的思路是数组纯模拟
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N];
int m,n;
string s;
void slove1(){
int b[N],c[N];int x,y;;cin>>x;for(int i=0;i<x;i++)cin>>b[i];cin>>y;for(int i=0;i<y;i++)cin>>c[i];int i=1,j=0;while(i<=n){if(a[i]==b[j])j++;else j=0;if(j==x)break;i++; } if(j==x){int d[N],cnt=0;for(int p=i+1;p<=n;p++)d[cnt++]=a[p]; int p,q;for(p=i-x+1,q=0;q<y;q++,p++)a[p]=c[q]; for(q=p,i=0;i<cnt;i++)a[q++]=d[i];n=q-1;}
}
void slove2(){for(int i=1;i<n;i++){if((a[i]+a[i+1])%2==0){int b[N];int k=(a[i]+a[i+1])/2;int cnt=0;for(int j=0,p=i+1;p<=n;p++,j++){b[j]=a[p];cnt++;}a[i+1]=k; for(int j=i+2,p=0;p<cnt;j++,p++){a[j]=b[p];} n++;i++;} }
}
void slove3(){int i,j;cin>>i>>j;int k[j-i+10];for(int p=0,q=i;q<=j;q++,p++){k[p]=a[q];}for(int p=j-i,q=i;q<=j;q++,p--){a[q]=k[p];}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=0;i<m;i++){int x;cin>>x;if(x==1){slove1();}else if(x==2){slove2(); }else if(x==3){slove3(); }
}
cout<<a[1];for(int i=2;i<=n;i++)
cout<<" "<<a[i];
} 7.大幂数
【解析】数据范围不是很大,可以暴力枚举
#include<bits/stdc++.h>
using namespace std;
int main(){int n;cin>>n;int f=0;int res,c;//降幂寻找// 2<n<2^31 意味着幂次最大为31 for(int i=31;i>=1;i--){//必须开long long 否则会爆!!! long long sum=1,j=2;while(sum<n){sum+=pow(j,i);if(sum==n){f=1;res=j;c=i;break;}j++;}//最大幂找到后退出 if(f)break; }if(f){printf("1^%d",c);for(int l=2;l<=res;l++)printf("+%d^%d",l,c);}else printf("Impossible for %d.",n);
} 8.现代战争
【解析】模拟
#include<bits/stdc++.h>
using namespace std;
long long g[1010][1010];
long long max_x=-0x3f3f3f3f3f;
int main(){int n,m,k;cin>>n>>m>>k;int x,y; for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>g[i][j];if(g[i][j]>=max_x){x=i,y=j;max_x=g[i][j];}}}while(k--){for(int p=1;p<=n;p++){g[p][y]=-0x3f3f3f3f3f;}for(int p=1;p<=m;p++){g[x][p]=-0x3f3f3f3f3f;}max_x=-0x3f3f3f3f;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(g[i][j]>=max_x){x=i,y=j;max_x=g[i][j];}} }
}
int c1=1;for(int i=1;i<=n;i++){int c=1,f=0;for(int j=1;j<=m;j++){if(!f&&g[i][j]!=-0x3f3f3f3f3f){f=1;cout<<g[i][j];}else if(g[i][j]!=-0x3f3f3f3f3f&&f){cout<<" "<<g[i][j];}}if(c1<=n-k&&f)cout<<endl;if(f)c1++;
}
}9.算式拆解

【解析】这个题就是模拟栈的过程
#include<bits/stdc++.h>
using namespace std;
char s[150];
vector<char> h,k;
int main(){scanf("%s",s);for(int i=0;i<strlen(s);i++){
//当遇到")"弹出if(s[i]==')') {while(h.size()&&h.back()!='('){char x=h.back();h.pop_back();k.push_back(x);}h.pop_back();while(k.size()){char x=k.back();k.pop_back();cout<<x; }cout<<endl;}else h.push_back(s[i]);
}
}10.三点共线

【解析】这个地方我直接用的暴力枚举和离散化处理。这题也有一个前置条件,即满足共线的条件x2=2*x1-x0。
#include<bits/stdc++.h>
using namespace std;
int n;
//便于离散化处理
const int N=4e6;
vector<int>a,b;
bool c[2*N+10];
int main(){cin>>n;//输入for(int i=0;i<n;i++){int x,y;cin>>x>>y;if(y==0)a.push_back(x);else if (y==1)b.push_back(x);else c[x+N]=true; }//进行去重,防止重复遍历sort(a.begin(),a.end());sort(b.begin(),b.end());a.erase(unique(a.begin(),a.end()),a.end());b.erase(unique(b.begin(),b.end()),b.end());//暴力枚举int k=0;for(int j=0;j<b.size();j++){for(int i=0;i<a.size();i++){
//满足共线条件int x3=2*b[j]-a[i];//离散化操作if(c[x3+N]){k=1;printf("[%d, 0] [%d, 1] [%d, 2]\n",a[i],b[j],x3);
}}
}
if(k==0)
cout<<-1;
}11.胖达的山头

【解析】1.区间分组问题
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
struct Range{int l,r;
}range[N];
bool cmp(Range x,Range y)
{return x.l<y.l;
}
int main()
{int n;cin>>n;for(int i=0;i<n;i++){
string a,b;
cin>>a>>b;
int p=0,q=0;for(int i=0;i<a.size();i++){if(a[i]!=':')p*=10,p+=a[i]-'0';
}
for(int i=0;i<b.size();i++){if(b[i]!=':')q*=10,q+=b[i]-'0';
}
range[i].l=p;
range[i].r=q;
}sort(range,range+n,cmp);priority_queue<int,vector<int>,greater<int>> heap;for(int i=0;i<n;i++){if(heap.empty()||heap.top()>=range[i].l) heap.push(range[i].r);else {heap.pop();heap.push(range[i].r);}}cout<<heap.size();return 0;
}2.将题目转化为在同一时刻最多有多少只胖达同时处于活跃状态,这个最大并发活跃数就是我们最少需要的山头数量,利用差分来写。具体的可以看PAT 2025天梯赛L2-3. 胖达的山头 - AcWing
#include<bits/stdc++.h>
using namespace std;
const int N=250000;
int sum[N];
int n;
int main(){cin>>n;
getchar();
memset(sum,0,sizeof(sum));
for(int i=0;i<n;i++){
string a,b;
cin>>a>>b;
int p=0,q=0;for(int i=0;i<a.size();i++){if(a[i]!=':')p*=10,p+=a[i]-'0';
}
for(int i=0;i<b.size();i++){if(b[i]!=':')q*=10,q+=b[i]-'0';
}
sum[p+1]++;
sum[q+2]--;
}
int ans=0;
for(int i=1;i<N;i++){sum[i]+=sum[i-1];ans=max(ans,sum[i]);
}
cout<<ans;
}12.被n整除的n位数

【解析】 dfs直接进行暴力搜索。
#include<bits/stdc++.h>
using namespace std;
long long a,b;
int n;
int k[20];
int f=0;
void dfs(int x,long long s){if(x==n){if(s>=a&&s<=b){cout<<s<<endl;f=1;}return ;}for(int i=0;i<=9;i++){long long k=s*10+i;
//回溯前进行判断是否能够被当前位置整除,剪枝if(k%(x+1)==0)dfs(x+1,s*10+i);}}
int main(){cin>>n;cin>>a>>b;
//这里没有保证a,b也是n位数,所以我们要用to_string函数,不能用a-pow(10,n-1)int l=to_string(a)[0]-'0';int r=to_string(b)[0]-'0';for(int i=l;i<=r;i++)dfs(1,i); if(!f)cout<<"No Solution";
}相关文章:

2025年GPLT团体程序设计天梯赛L1-L2
目录 1.珍惜生命 2.偷感好重 3.高温补贴 4.零头就抹了吧 5.这是字符串题 6.这不是字符串题 7.大幂数编辑 8.现代战争编辑 9.算式拆解 10.三点共线 11.胖达的山头 12.被n整除的n位数 1.珍惜生命 【解析】直接输出即可 #include<bits/stdc.h> using namespace…...

【每天一个知识点】IPv4(互联网协议版本4)和IPv6(互联网协议版本6)
IPv4(互联网协议版本4)和IPv6(互联网协议版本6)是用于在互联网上标识和定位设备的两种主要协议。它们的主要区别在于地址空间、结构、以及一些附加功能。以下是两者的对比: 1. 地址长度 IPv4: 地址长度为32位…...

金仓数据库征文-政务领域国产化数据库更替:金仓 KingbaseES 应用实践
目录 一.金仓数据库介绍 二.政务领域数据库替换的时代需求 三.金仓数据库 KingbaseES 在政务领域的替换优势 1.强大的兼容性与迁移能力 2.高安全性与稳定性保障 3.良好的国产化适配性 四.金仓数据库 KingbaseES 在政务领域的典型应用实践 1.电子政务办公系…...

Mac 「brew」快速安装MySQL
安装MySQL 在 macOS 上安装 MySQL 环境可以通过Homebrew快速实现,以下是步骤指南: 方法 1:使用 Homebrew 安装 MySQL 1. 安装 Homebrew 如果尚未安装 Homebrew,可以通过以下命令安装: /bin/bash -c "$(curl -…...

Android Studio开发中Application和Activity生命周期详解
文章目录 Application生命周期Application生命周期概述Application关键回调方法onCreate()onConfigurationChanged()onLowMemory()onTrimMemory()onTerminate() Application生命周期管理最佳实践 Activity生命周期Activity生命周期概述Activity生命周期回调方法onCreate()onSta…...

【一次成功!】Ubuntu22.04 安装 Autoware、 cuda、 cudnn、 TensorRT
背景 新买的工控机,32GB NVIDIA GeForce RTX 4060,只装了 Ubuntu22.04、ROS2 Humble。 一.安装Autoware Source installation - Autoware Documentation 1. 基础环境 OS Ubuntu 22.04ROS ROS 2 Humble#小鱼ros一键安装 wget http://fishros.com/install -O fishros &…...

【金仓数据库征文】金仓数据库:开启未来技术脑洞,探索数据库无限可能
我的个人主页 我的专栏: 人工智能领域、java-数据结构、Javase、C语言,希望能帮助到大家!!! 点赞👍收藏❤ 目录 引言:数据库进化的下一站 —— 未来科技的无限可能金仓数据库简介:国…...

微信小程序根据图片生成背景颜色有效果图
效果图 取得是图片中间10个像素算出背景颜色 .wxml <canvas type"2d" id"imageCanvas" style"--w: {{w}}px;--h: {{h}}px;" /> <view style"background: {{backgroundColor}};"><image bind:tap"updateIndex&qu…...

Redis ⑥-string | hash | list
string类型基本介绍 Redis 中的字符串,是直接按照二进制的方式进行存储的。也就是说,在存取的过程中,是不会做任何编码转换的。存的是啥,取的时候就是啥。 Redis 的这个机制,就使得 Redis 非常适合用来存储各种各样的…...

深入理解C语言函数之模拟实现strcpy()strcat()
文章目录 前言一、strcpy的模拟实现二、strcat的模拟实现总结 前言 前面我们用三种方法模拟实现了一下strlen,所以这篇文章模拟实现以下strcpy()strcat() 一、strcpy的模拟实现 首先我们去官网找到strcpy的用法和原…...

大数据组件学习之--Kafka 安装搭建
一、前置环境 在搭建kafka之前,请确认自己的hadoop、zookeeper是否搭建完成且可正常运行 二、下载并上传安装包(链接为百度网盘) kafka安装包 tar -zxvf /opt/software/kafka_2.12-2.4.1.tgz -C /opt/module/ 进入解压后的目录更改文件名…...

BIOS主板(非UEFI)安装fedora42的方法
BIOS主板(非UEFI)安装fedora42的方法 现实困难:将Fedora-Workstation-Live-42-1.1.x86_64.iso写入U盘制作成可启动U盘启动fedora42,按照向导将fedora42安装到真机的sda7分区中得到报错如下内容: /boot/efi 必需的 /boot/efi必须位于格式化为e…...

[吾爱出品] 【键鼠自动化工具】支持识别窗口、识图、发送文本、按键组合等
键鼠自动化工具 链接:https://pan.xunlei.com/s/VOOhDZkj-E0mdDZCvo3jp6s4A1?pwdfufb# 1、增加的找图点击功能(不算增加,只能算缝补),各种的不完善,但是能运行。 2、因为受限于原程序的界面,…...

图解YOLO(You Only Look Once)目标检测(v1-v5)
1. YOLO系列整体介绍 YOLO属于深度学习经典检测方法中的单阶段(one - stage)类型,与两阶段(two - stage,如Faster - rcnn、Mask - Rcnn系列)方法相对。 不同模型性能 单阶段方法的最核心优势是速度非常快…...

基于AI应用创业IDEA:使用百度搜索开放平台的MCP广场智能推荐MCPServices服务
基于AI应用创业IDEA:使用百度搜索开放平台的MCP广场智能推荐MCPServices服务 在当今快速发展的技术时代,人工智能(AI)已经成为推动各行各业创新的关键力量。特别是在创业领域,AI技术不仅能够帮助提升产品性能…...
WebRTC服务器Coturn服务器的管理平台功能
1、概述 开源的webrtc服务器提供管理平台功能,用户可以通过web页面进行访问配置coturn服务器,主要包括管理平台功能和telnet的管理功能,coturn相当于telnet服务器,可能通过配置来开启这两个功能,方便查看coturn服务器…...
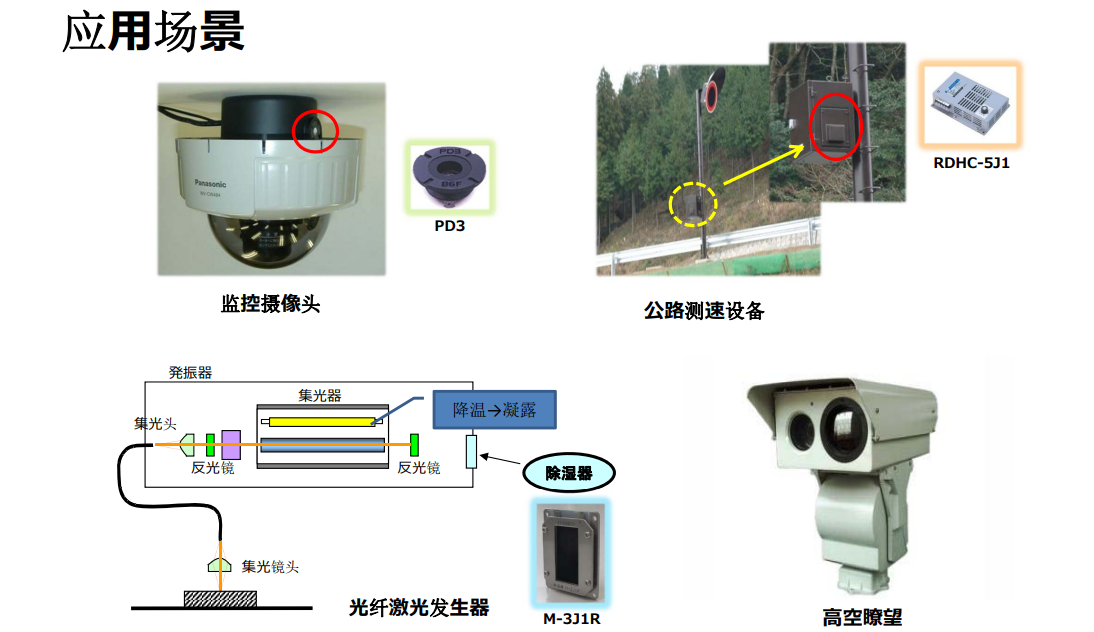
户外监控起雾终结者:PD3电解除湿器全方位解决方案
一、监控画面模糊?潮湿正在侵蚀您的安防系统! 清晨的浓雾中,监控画面逐渐模糊;暴雨过后,摄像头内部凝结水珠;冬季温差导致镜头起雾,关键画面完全丢失...这些场景每天都在全国各地的安防系统中上…...

[mysql]数据类型精讲
目录 数据类型精讲: 整数类型 浮点类型 日期和时间类型 文本字符串类型 数据类型精讲: 精度问题:不能损失数据 性能问题:表的设计,范式的讲解. 表设计的时候需要设置字段,我们现在要把字段类型讲完.,细节点一点点给大家拆解. Float和double是有精度的损失的,这边推荐使用…...

并发设计模式实战系列(7):Thread Local Storage (TLS)
🌟 大家好,我是摘星! 🌟 今天为大家带来的是并发设计模式实战系列,第七章Thread Local Storage (TLS),废话不多说直接开始~ 目录 一、核心原理深度拆解 1. TLS内存模型 2. 关键特性 二、生活化类比&a…...

跟我学C++中级篇——处理对象的复制
一、对象的传递 在应用程序中,经常会遇到不同线程或不同模块间需要进行对象的传递,本来传递不是什么多大的事。但问题是,如果对象的值大到一定的程度后,传递不是问题可对象值的处理反而成了问题了。举一个现实世界的例子…...

Tailwind CSS 实战:基于 Kooboo 构建企业官网页面(一)
目录 一、技术选型:为什么选择Tailwind Kooboo? 二、CDN方案 vs 传统安装 三、CDN方式实战步骤 一、技术选型:为什么选择Tailwind Kooboo? 1.1 黄金组合优势 Tailwind CSS:原子化CSS框架,提供&#x…...

Go语言实战:快速搭建完整的用户认证系统
前言 在本文中,我将介绍如何使用 Go 语言搭建一个包含用户注册、登录、登出功能的完整认证系统。该系统使用 SQLite 作为数据库,JWT 作为身份验证token,并实现了优雅关闭等特性。 技术栈 Go 语言 SQLite 数据库 JWT (JSON Web Token) G…...

Bolsig+超详细使用教程
文章目录 Bolsig介绍Bolsig的使用 Bolsig介绍 BOLSIG 是一款用于求解弱电离气体中电子玻尔兹曼方程的免费计算程序,适用于均匀电场条件下的群体实验、气体放电及碰撞型低温等离子体研究。在此类环境中,电子分布函数呈现非麦克斯韦特性,其形态…...

uni-app云开发总结
uni-app云开发总结 云开发无非就三个概念:云数据库、云函数、云存储 uni-app中新增了一个概念叫做云对象,它其实就是云函数的加强版,它是导出的一个对象,对象中可以包含多个操作数据库的函数,接下来咱们就详细对uni-…...

新闻速递丨Altair 与 Databricks 达成合作,加速数据驱动型创新
NEWS Altair 近日宣布与数据和人工智能公司 Databricks 达成战略合作,通过新一代数据统一化、图谱驱动智能和企业级人工智能(AI)技术赋能双方客户。 此次合作整合了两大平台的核心优势,将 Altair RapidMiner 平台的强大功能&…...

vscode和git 踩坑
git init经常 在 vscode push错误问题: 正确姿势:先 GitHub 上建仓库 → git clone 拉到本地 → 再用 VSCode 打开编辑 ❌ 不是:VSCode 里 git init → 再去 GitHub 选个仓库绑定 举个对比 操作流程是否推荐后果GitHub 创建仓库 → git clone → 用 VSC…...

《ATPL地面培训教材13:飞行原理》——第7章:失速
翻译:刘远贺;工具:Cursor & Cluade 3.7 第7章:失速 目录 引言失速的原因升力曲线失速恢复接近失速时的飞机行为接近失速时的飞行控制使用失速识别失速速度失速警告人工失速警告装置基本失速要求(EASA和FAR&…...

在html中如何创建vue自定义组件(以自定义文件上传组件为例,vue2+elementUI)
1、先上代码:vueUpload.js var dom <div class"upload-file"><el-upload :action"uploadFileUrl" :before-upload"handleBeforeUpload" :file-list"fileList" :limit"limit":on-error"handleUpl…...

《使用 Cesium 加载静态热力图显示的实现步骤》
Cesium——使用cesium 加载静态热力图显示 实现思路 要在 Cesium 中加载静态热力图,我们需要完成以下几个主要步骤: 1、计算热力图数据的四至范围和中心点。 2、初始化热力图并设置相关参数。 3、将数据添加到热力图中。 4、定位到热力图的位置并刷…...

Spring 事务传播行为
事务传播行为(Transaction Propagation Behavior)是指多个拥有事务的方法在嵌套调用时的事务控制方式。以下是常见的事务传播行为及其应用场景: 1. PROPAGATION_REQUIRED(默认) 定义:如果当前存在事务&…...
