代码随想录算法训练营第60期第十七天打卡
今天我们继续进入二叉树的下一个章节,今天的内容我在写今天的博客前大致看了一下部分题目难度不算大,那我们就进入今天的题目。
第一题对应力扣编号为654的题目最大二叉树
这道题目的坑相当多,我第一次题目没有看明白就是我不知道到底是如何构造出这棵二叉树的,我就直接看了视频讲解,现在我们先来看一下题目:

我们先看一下示例是什么意思,注意力扣上是这样解释的:

首先找出最大值,然后分割数组找到左边部分与右边部分然后递归构造出根节点的左子树与右子树就可以了,这样我才明白这道题目究竟是什么意思,既然要构造二叉树大家记住,我们大概率会选用前序遍历,为什么呢?因为我们构造二叉树一定是先要从根节点出发才能逐步构建起它的左子树与右子树进而递归构造出整棵二叉树,这个是大家一定要去了解的,后来看完讲解我发现这道题与我们昨天的最后一道题有异曲同工之妙,其实都还是递归构建,当然我们这里是需要先找出最大的元素作为根节点,随后我们就可以找到左子树与右子树,递归构建就可以了,我要说明一下注意我们后来的数组是左闭右开的,一定注意,我们传入数组递归构建就可以,我将代码放到下面大家可以自行参考:
class Solution {
public:TreeNode* constructMaximumBinaryTree(vector<int>& nums) {TreeNode* node = new TreeNode(0);//特殊情况要考虑上不要忘记if (nums.size() == 1) return new TreeNode(nums[0]);//那为什么没有考虑数组为空的情况呢?因为题目说了数组的大小是大于等于1的int maxValue = 0;//定义最大值int index = 0;//定义最大值的下标for (int i = 0; i < nums.size(); ++i){if (nums[i] > maxValue){maxValue = nums[i];index = i;}}node -> val = maxValue;//构造左子树if (index > 0){vector<int> newVec(nums.begin(), nums.begin() + index);node->left = constructMaximumBinaryTree(newVec);}//构造右子树if (index < (nums.size() - 1)){vector<int> newVec(nums.begin() + index + 1, nums.end());node -> right = constructMaximumBinaryTree(newVec);}return node;}
};那其实这道题目还有优化版本的代码大家可以发现我需要构造新的数组来存储左右子数,这样其实又耗时又耗空间,这里我再给出优化版的代码:
class Solution {
private:// 在左闭右开区间[left, right),构造二叉树TreeNode* traversal(vector<int>& nums, int left, int right) {if (left >= right) return nullptr;// 分割点下标:maxValueIndexint maxValueIndex = left;for (int i = left + 1; i < right; ++i) {if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;}TreeNode* root = new TreeNode(nums[maxValueIndex]);// 左闭右开:[left, maxValueIndex)root->left = traversal(nums, left, maxValueIndex);// 左闭右开:[maxValueIndex + 1, right)root->right = traversal(nums, maxValueIndex + 1, right);return root;}
public:TreeNode* constructMaximumBinaryTree(vector<int>& nums) {return traversal(nums, 0, nums.size());}
};这样就可以避免申请新的空间来重新建立数组,我们直接使用下标操作,不过建议大家先把最基础的版本搞明白其实就可以了。这道题目我就先分享到这里,接下来我们看下一道题目。
第二题对应力扣编号为617的题目合并二叉树
那这道题是什么意思呢?其实是将两棵树相对应位置的节点的数值相加最后可以得到一棵新的二叉树,我们来看一下具体的题目:

我们应该如何考虑这道题目呢?其实这道题目难点就在于它是同时操作两棵二叉树,而我们平时刷的题都是操作一棵二叉树,但是我希望这道题过后大家可以掌握应该如何同时操作两棵二叉树,首先大家要知道一点就是如果我在合并的过程中我如果其中一棵二叉树的当前的节点是空,其实我的新合并出来的二叉树就应该是另一棵二叉树的所对应节点的值,如果两棵二叉树都为空,那其实新二叉树的对应节点也为空,随后我们递归构建左子树与右子树就可以,最后返回根节点,当然我下面提供的代码是我在tree1的基础上更新,其实大家也可以开一棵新的二叉树,在这里我就提供一下更新版本的代码,如果开新的二叉树版本大家感兴趣的话可以去代码随想录网站去看:
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if (root1 == NULL) return root2;if (root2 == NULL) return root1;//if (root1 == NULL && root2 == NULL) return NULL;//其实两棵树的对应节点都为空的情况已经包含了(上面这一句可以不写)root1 -> val += root2 -> val;root1 -> left = mergeTrees(root1 -> left, root2 -> left);root1 -> right = mergeTrees(root1 -> right, root2 -> right);return root1;}
};第三题对应力扣编号为700的二叉搜索树中的搜索
在这里我们就引入了二叉搜索树了,我们先复习一下什么样的树叫做二叉搜索树,其实是左子树的所有数值小于根节点,右子树的所有数值大于根节点就是二叉搜索树,我们了解了定义以后我们一起来看一下题目:

我看到示例就大致明白了题目的具体要求了,其实题目给我们的是一个层序遍历和一个节点的值,要求我们返回以该节点为根的子树,那我们如何解决这道题目呢?其实这道题目的递归法与迭代法都不难理解,我两种思路都给大家展示一下,首先题目就很好利用了二叉搜索树的性质,其实我们是可以利用二叉搜索树的性质来判断我们当前搜索的是在左子树还是右子树,就是与根节点的值进行比较,如果小就说明我们目前在左子树,如果大说明我们目前在右子树,那这样我们可以写出如下的递归代码:
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == NULL || root -> val == val) return root;TreeNode* result = NULL;//这时候在左子树if (root -> val > val){//注意我们使用一个临时变量来存储我们找到的值result = searchBST(root -> left, val);}//这时候在右子树 else if (root -> val < val){result = searchBST(root -> right, val);}return result;}
};接下来我们来看一下迭代法如何写,其实我们原来是不是写过迭代法,我们一些用到迭代法都是会用栈或者队列去模拟深度遍历和广度遍历,但这里我们考虑到二叉搜索树的特殊性,其实我们不需要这么麻烦了,它的节点是有序的我们就不需要四处搜索了,我们看一下代码是如何写的:
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {while (root != NULL) {if (root->val > val) root = root->left;else if (root->val < val) root = root->right;else return root;}return NULL;}
};第四题验证二叉搜索树对应力扣编号98
我们上一道题已经刷到过关于二叉搜索树的题目,这一道题是让我们验证二叉搜索树,我们看一下题目到底是怎么说的:

其实题目要求很简单了,那么我们应该如何解决呢?其实这道题目有点那种数学题的感觉叫做“会者不难,难者不会”,我为啥这样说呢?因为如果大家知道一个二叉搜索树的性质其实就很简单了,我直接告诉大家,大家以后记住就可以了“中序遍历下,输出的二叉搜索树节点的数值是有序序列”,只要大家知道这个性质其实代码就很好写了,我们使用我们之前的迭代写法将这棵树的中序遍历的结果存储到一个数组里,然后判断这个数组是否有序就可以了,我可以直接给出代码:
class Solution {
private:vector<int> vec;void traversal(TreeNode *root){if (root == NULL) return;//左根右的中序遍历if (root -> left) traversal(root -> left);vec.push_back(root -> val);if (root -> right) traversal(root -> right);}
public:bool isValidBST(TreeNode* root) {vec.clear();//先清空traversal(root);//这样其实就将数组再次填满了for (int i = 1; i < vec.size(); ++i){if (vec[i] <= vec[i - 1]) return false;}return true;}
};这是一种最为直观的做法,大家务必要将这个技巧牢记于心,那其实还有其他方法,我们还是要注意我们二叉搜索树是左子树所有的节点都是小于根节点的,右子树所有的节点都是大于根节点的,千万不要不判断根节点与它的左右孩子的关系,这样是无法判断是不是二叉搜索树的,因为不符合我们二叉搜索树的定义,那我们应该如何判断呢?其实我们还是可以使用递归的,我们其实可以一直中序遍历,只要发现没有顺序的就可以直接return false,那我们的代码可以这样写:
class Solution {
public:long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值bool isValidBST(TreeNode* root) {if (root == NULL) return true;bool left = isValidBST(root->left);// 中序遍历,验证遍历的元素是不是从小到大if (maxVal < root->val) maxVal = root->val;else return false;bool right = isValidBST(root->right);return left && right;}
};就是说我们一直更新maxVal如果左子树的节点小于根节点的值那我就一直赋值如果发现有大于的这在左子树这边就说明不是二叉搜索树了,我们来看一下代码:
class Solution {
public:long long maxVal = LONG_MIN;bool isValidBST(TreeNode* root) {if (root == NULL) return true;bool left = isValidBST(root -> left);if (maxVal < root -> val) maxVal = root -> val;else return false;bool right = isValidBST(root -> right);return left && right;}
};这个其实还是中序遍历,左根右的顺序,我们先看左子树,只要当前节点不为空就一直递归,先左再右,最后发现到了叶子节点,最后将根节点赋值给maxVal,接着去判断右边,如果最后左右都为true就是二叉搜索树了,这个递归还有点难度,就是我们是如何递归的,先左一直到叶子节点会返回true,随后我们赋值,再去判断右子树,当右子树也到了叶子节点的时候也会返回 true,根节点的右子树是一个意思,最后我们判断是否是true, 我还是建议大家用上面的第一种方法理解,这个递归作为选学,上面的那一种方法必须会。
总结
今天的题目还是挺有意思的,我们也接触了二叉搜索树,最大二叉树是一道不错的题目,我们学会了递归与分割数组,合并二叉树其实还是递归,随后的两道题我们接触了二叉搜索树,大家自己要去消化一下,我们明天再见!
相关文章:

代码随想录算法训练营第60期第十七天打卡
今天我们继续进入二叉树的下一个章节,今天的内容我在写今天的博客前大致看了一下部分题目难度不算大,那我们就进入今天的题目。 第一题对应力扣编号为654的题目最大二叉树 这道题目的坑相当多,我第一次题目没有看明白就是我不知道到底是如何…...
)
小刚说C语言刷题——1565成绩(score)
1.题目描述 牛牛最近学习了 C 入门课程,这门课程的总成绩计算方法是: 总成绩作业成绩 20% 小测成绩 30% 期末考试成绩 50%。 牛牛想知道,这门课程自己最终能得到多少分。 输入 三个非负整数 A、B、C ,分别表示牛牛的作业成…...
SOC估算:开路电压修正的安时积分法
SOC估算:开路电压修正的安时积分法 基本概念 开路电压修正的安时积分法是一种结合了两种SOC估算方法的混合技术: 安时积分法(库仑计数法) - 通过电流积分计算SOC变化 开路电压法 - 通过电池电压与SOC的关系曲线进行校准 方法原…...
)
Spark-SQL(总结)
了解到Spark SQL是Spark用于结构化数据处理的模块,其前身是Shark。Shark基于Hive开发,但对Hive的依赖制约了Spark的发展。掌握了 Spark - SQL 的特点,如易整合、统一数据访问、兼容 Hive 以及支持标准数据连接,可处理多种数据源的…...
——Oracle安装和配置)
Oracle for Linux安装和配置(11)——Oracle安装和配置
11.3. Oracle安装和配置 Linux上Oracle的安装及配置与Windows上差不多,只是安装软件的准备等有所不同,下面只对不同于Windows的部分进行较为详细的讲解,其他类似部分不再赘述。另外,无论选择使用虚机还是物理机,Oracle安装、配置和使用等方面几乎都是完全一样的。 11.3.…...

【防火墙 pfsense】2配置
(1)接口配置和接口 IP 地址分配 ->配置广域网(WAN)和局域网(LAN)接口,分配设备标识符,如 eth0、eth1 等; ->如将WAN 接口将被分配到 eth0,而 LAN 接口将…...

使用 SSE + WebFlux 推送日志信息到前端
为什么使用 SSE 而不使用 WebSocket, 请看 SEE 对比 Websocket 的优缺点。 特性SSEWebSocket通信方向单向(服务器→客户端)双向(全双工)协议基于 HTTP独立协议(需 ws:// 前缀)兼容性现代浏览器(…...

Ollama 常见命令速览:本地大模型管理指南
Ollama 常见命令速览:本地大模型管理指南 一、什么是 Ollama? Ollama 是一个轻量级工具,允许用户在本地快速部署和运行大型语言模型(LLM),如 Llama、DeepSeek、CodeLlama 等。其命令行工具设计简洁&#…...

C++开发之设计模式
设计模式存在的意义 设计模式提供了经过验证的解决方案,帮助开发者在不同的项目中重用这些解决方法,减少重复劳动,提高代码的复用性。设计模式通常遵循面向对象的设计原则,如单一职责原则、开放封闭原则等,能够帮助开…...

AWS Glue ETL设计与调度最佳实践
一、引言 在AWS Glue中设计和调度ETL过程时,需结合其无服务器架构和托管服务特性,采用系统化方法和最佳实践,以提高效率、可靠性和可维护性。本文将从调度策略和设计方法两大维度详细论述,并辅以实际案例说明。 二、调度策略的最…...
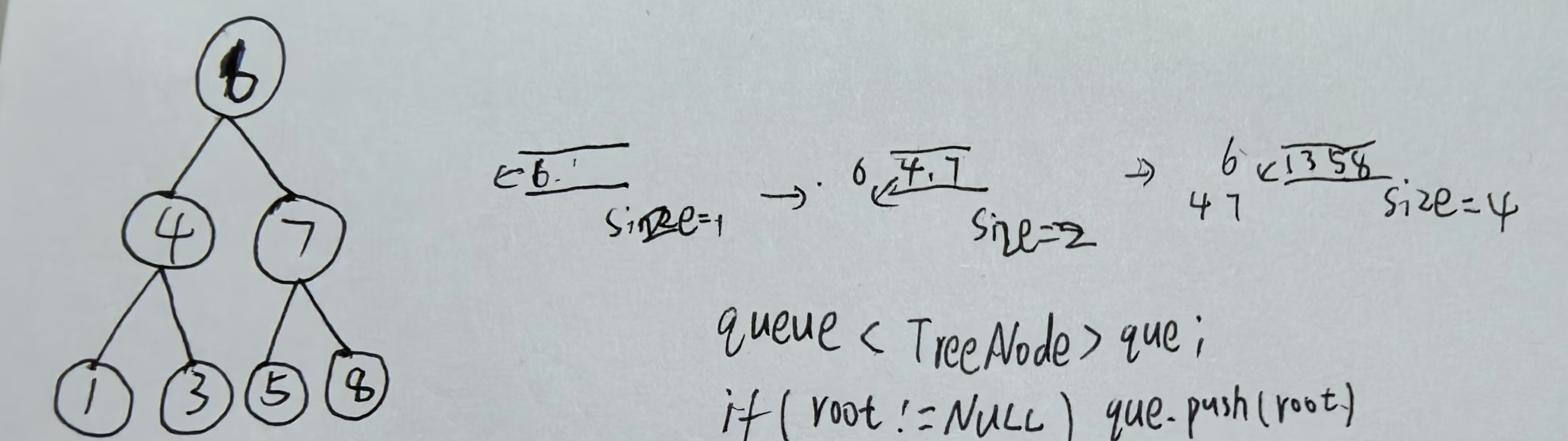
二叉树的遍历(广度优先搜索)
二叉树的第二种遍历方式,层序遍历,本质是运用队列对二叉树进行搜索。 层序遍历是指将二叉树的每一层按顺序遍历,通过队列实现就是先将根节点push入队,统计此时的队列中的元素数量size,将size元素全部pop出去࿰…...

JavaScript 里创建对象
咱们来用有趣的方式探索一下 JavaScript 里创建对象的各种“魔法咒语”! 想象一下,你是一位魔法工匠,想要在你的代码世界里创造各种奇妙的“魔法物品”(也就是对象)。你有好几种不同的配方和工具: 1. 随手捏造(对象字面量 {}) 场景:你想快速做一个独一无二的小玩意儿…...

2025年计算机视觉与智能通信国际会议(ICCVIC 2025)
2025 International Conference on Computer Vision and Intelligent Communication 一、大会信息 会议简称:ICCVIC 2025 大会地点:中国杭州 收录检索:提交Ei Compendex,CPCI,CNKI,Google Scholar等 二、会议简介 2025年计算机视觉与智能通…...

手工收集统计信息
有时想对某些表收集统计信息 CREATE OR REPLACE PROCEDURE GATHER_STATS ASDECLAREV_SQL1 VARCHAR(1000);--表游标CURSOR C1 ISSELECT (SELECT USER) AS TABLE_OWNER,TABLE_NAMEFROM USER_TABLES; --可以在这里加过滤条件--索引游标CURSOR C2 ISSELECT TABLE_OWNER,INDEX_NAM…...

flume整合Kafka和spark-streaming核心编程
flume整合Kafka 需求1:利用flume监控某目录中新生成的文件,将监控到的变更数据发送给kafka,kafka将收到的数据打印到控制台: 1.查看topic 2.编辑flume-Kafka.conf,并启动flume 3.启动Kafka消费者 4.新增测试数据 5.查…...

tokenizer的用法
下面介绍下基于 Hugging Face Transformers 库中 tokenizer(分词器)的主要用法和常用方法,帮助你了解如何在各种场景下处理文本。这里以 AutoTokenizer 为例,但大多数模型对应的 tokenizer 用法大同小异。 ───────────…...
)
kotlin和MVVM的结合使用总结(二)
MVVM 架构详解 核心组件:ViewModel 和 LiveData 在 Android 中,MVVM 架构主要借助 ViewModel 和 LiveData 来实现。ViewModel 负责处理业务逻辑,而 LiveData 则用于实现数据的响应式更新。 ViewModel 的源码分析 ViewModel 的核心逻辑在 …...

Git 入门知识详解
文章目录 一、Git 是什么1、Git 简介2、Git 的诞生3、集中式 vs 分布式3.1 集中式版本控制系统3.2 分布式版本控制系统 二、GitHub 与 Git 安装1、GitHub2、Git 安装 一、Git 是什么 1、Git 简介 Git 是目前世界上最先进的分布式版本控制系统。版本控制系统能帮助我们更好地管…...

React.memo 和 useMemo
现象 React 中,通常父组件的某个state发生改变,会引起父组件的重新渲染(和其他state的重新计算),从而会导致子组件的重新渲染(和其他非相关属性的重新计算) 问题一:如何避免因为某个…...

EDI 如何与 ERP,CRM,WMS等系统集成
在数字化浪潮下,与制造供应链相关产业正加速向智能化供应链转型。传统人工处理订单、库存和物流的方式已难以满足下单客户对响应速度和数据准确性的严苛要求。EDI技术作为企业间数据交换的核心枢纽,其与ERP、CRM、WMS等业务系统的深度集成,成…...

面试踩过的坑
1、 “”和equals 的区别 “”是运算符,如果是基本数据类型,则比较存储的值;如果是引用数据类型,则比较所指向对象的地址值。equals是Object的方法,比较的是所指向的对象的地址值,一般情况下,重…...

论文阅读:2024 ACL ArtPrompt: ASCII Art-based Jailbreak Attacks against Aligned LLMs
总目录 大模型安全相关研究:https://blog.csdn.net/WhiffeYF/article/details/142132328 Artprompt: Ascii art-based jailbreak attacks against aligned llms https://www.doubao.com/chat/3846685176618754 https://arxiv.org/pdf/2402.11753 https://github…...

多物理场耦合低温等离子体装置求解器PASSKEy2
文章目录 PASSKEy2简介PASSKEY2计算流程PASSKEy2 中求解的物理方程电路模型等离子体模型燃烧模型 PASSKEy2的使用 PASSKEy2简介 PASSKEy2 是在 PASSKEy1 的基础上重新编写的等离子体数值模拟程序。 相较于 PASSKEy1, PASSKEy2 在具备解决低温等离子体模拟问题的能力…...

视频噪点多,如何去除画面噪点?
你是否遇到过这样的困扰?辛辛苦苦拍摄的视频,导出后却满屏 “雪花”,夜景变 “噪点盛宴”,低光环境秒变 “马赛克现场”? 无论是日常拍摄的vlog、珍贵的家庭录像,还是专业制作的影视作品,噪点问…...

09前端项目----分页功能
分页功能 分页器的优点实现分页功能自定义分页器先实现静态分页器调试分页器动态数据/交互 Element UI组件 分页器的优点 电商平台同时展示的数据很多,所以采用分页功能实现分页功能 Element UI已经有封装好的组件,但是也要掌握原理,以及自定…...

第十二届蓝桥杯 2021 C/C++组 直线
目录 题目: 题目描述: 题目链接: 思路: 核心思路: 两点确定一条直线: 思路详解: 代码: 第一种方式代码详解: 第二种方式代码详解: 题目:…...

《Piper》皮克斯技术解析:RIS系统与云渲染如何创造奥斯卡级动画短片
本文由专业专栏作家 Mike Seymour 撰写,内容包含非常有价值的行业资讯。 译者注 《Piper》是皮克斯动画工作室的一部技术突破性的短片,讲述了一只小鸟在海滩上寻找食物并面对自然挑战的故事。它不仅凭借其精美的视觉效果和细腻的情感表达赢得了2017年奥…...

Java在excel中导出动态曲线图DEMO
1、环境 JDK8 POI 5.2.3 Springboot2.7 2、DEMO pom <dependency><groupId>org.apache.poi</groupId><artifactId>poi-ooxml</artifactId><version>5.2.3</version></dependency><dependency><groupId>commons…...

第19章:Multi-Agent多智能体系统介绍
第19章:Multi-Agent多智能体系统介绍 欢迎来到多智能体系统 (Multi-Agent System, MAS) 的世界!在之前的章节中,我们深入探讨了单个 AI Agent 的构建,特别是结合了记忆、上下文和规划能力的 MCP 框架。然而,现实世界中的许多复杂问题往往需要多个智能体协同工作才能有效解…...

Kotlin Multiplatform--02:项目结构进阶
Kotlin Multiplatform--02:项目结构进阶 引言正文 引言 在上一章中,我们对 Kotlin Multiplatform 项目有了基本的了解,已经可以进行开发了。但我们只是使用了系统默认的项目结构。本章介绍了如何进行更复杂的项目结构管理。 正文 在上一章中&…...
