[OpenGL] Lambertian材质漫反射BRDF方程的解释与推导
一、简介
本文简单的介绍了 Physical Based Rendering, PBR 中的 Lambertian 材质漫反射BRDF公式 f r l a m b e r t i a n = c d i f f π fr_{lambertian}=\frac{c_{diff}}{\pi} frlambertian=πcdiff的推导。
二、漫反射项
根据 渲染方程:
L o ( v ) = ∫ Ω f r ( l , v ) L i ( l ) ∗ ( n ⋅ l ) d l (1) Lo(v) = \int_{\Omega}fr(l,v)Li(l)*(n\cdot l) dl \tag{1} Lo(v)=∫Ωfr(l,v)Li(l)∗(n⋅l)dl(1)
其中的 BRDF 函数 f r ( l , v ) fr(l,v) fr(l,v) 定义如下:
f r ( l , v ) = k d ∗ f r l a m b e r t ( l , v ) + k s ∗ f r s p e c u l a r ( l , v ) (2) fr(l,v) = k_d * fr_{lambert}(l,v) + k_s*fr_{specular}(l,v)\tag{2} fr(l,v)=kd∗frlambert(l,v)+ks∗frspecular(l,v)(2)
其中 k d k_d kd 为漫反射的比例, f r l a m b e r t fr_{lambert} frlambert为漫反射中的 BRDF 函数定义如下:
f r l a m b e r t = c d i f f π (3) fr_{lambert} = \frac{c_{diff}}{\pi} \tag{3} frlambert=πcdiff(3)
其中 c d i f f c_{diff} cdiff 为描述材质属性的漫反射颜⾊(diffuse) c d i f f c_{diff} cdiff ,或者反照率(albedo) ρ \rho ρ。本文接下来介绍什么是 Lambertian 表面,为什么 Lambertian 材质的漫反射BRDF 公式如公式(3) 所示。
1. Lambert 表面
Lambertian 材质是指那种理想的完全漫反射表面,从任何观察方向看去,它反射的亮度都是一致的。即,不论外界的光照如何,Lambertian 材质满足以下公式:
L o ( v ) = ∫ Ω f r l a m b e r t i a n ( l , v ) ( n ⋅ l ) d l = L o c (4) Lo(v) = \int_{\Omega}fr_{lambertian}(l,v)(n\cdot l)\ dl = Lo_{c} \tag{4} Lo(v)=∫Ωfrlambertian(l,v)(n⋅l) dl=Loc(4)
不管视线向量 v v v 如何变化(需要保证在材质的上半球内),其出射的 radiance L o ( v ) Lo(v) Lo(v) 恒等于定值 L o c Lo_{c} Loc。
2. 漫反射公式解释
2.1 反照率 albedo
Lambertian BRDF 的恒定反射率通常被称为漫反射颜⾊(diffuse) c d i f f c_{diff} cdiff ,或者反照率(albedo) ρ \rho ρ。反照率 ρ \rho ρ描述了目标表面反射的辐射通量 Φ o u t \Phi_{out} Φout与入射的辐射通量 Φ i n \Phi_{in} Φin 之比。定义如下:
c d i f f = ρ = Φ o u t Φ i n (5) c_{diff} = \rho = \frac{\Phi_{out}}{\Phi_{in}} \tag{5} cdiff=ρ=ΦinΦout(5)
2.2 能量守恒定律
根据能量守恒定理定律,应该有:
c d i f f = ρ = Φ o u t Φ i n ≤ 1.0 (6) c_{diff} = \rho = \frac{\Phi_{out}}{\Phi_{in}} \le 1.0 \tag{6} cdiff=ρ=ΦinΦout≤1.0(6)
2.3 漫反射 BRDF 函数推导
接下来我们将基于以下假设和定义,推导得到 漫反射 BRDF 的渲染公式(3)。
2.3.1 已知信息
- 漫反射BRDF满足渲染方程: L o ( v ) = ∫ f r l a m b e r t i a n ( l , v ) ∗ L i ( l ) ∗ ( n ⋅ l ) d l Lo(v)=\int{fr_{lambertian}(l,v)*Li(l)*(n\cdot l)\ dl} Lo(v)=∫frlambertian(l,v)∗Li(l)∗(n⋅l) dl。
- 对于 Lambertian 材质, f r l a m b e r t i a n ( l , v ) fr_{lambertian}(l,v) frlambertian(l,v) 与 v v v 和 l l l 无关,即 f r l a m b e r t i a n ( l , v ) fr_{lambertian}(l,v) frlambertian(l,v) 是定值 f r c fr_{c} frc 。那么根据渲染方程,不管如何光照 L i ( l ) Li(l) Li(l) 如何分布,任意出射方向的 L o ( v ) Lo(v) Lo(v) 也都相等。
- 对于 Lambertian 材质,假设其没有自发光,满足能量守恒定理,即: c d i f f = ρ = Φ o u t Φ i n ≤ 1.0 c_{diff} = \rho = \frac{\Phi_{out}}{\Phi_{in}} \le 1.0 cdiff=ρ=ΦinΦout≤1.0。
- 目标表面的入射/出射辐射通量/功率(Radiant flux/Power) Φ i n \Phi_{in} Φin、 Φ o u t \Phi_{out} Φout 的计算公式如下:
Φ i n t = ∫ Ω L i ( l ) ∗ ( n ⋅ l ) d l d A Φ o u t = ∫ Ω L o ( v ) ∗ ( n ⋅ v ) d v d A \Phi_{int} = \int_{\Omega} Li(l)*(n\cdot l) dl\ dA \\ \Phi_{out} = \int_{\Omega} Lo(v)*(n\cdot v) dv\ dA Φint=∫ΩLi(l)∗(n⋅l)dl dAΦout=∫ΩLo(v)∗(n⋅v)dv dA - 假设目标表面为 Lambertian 材质,即只有漫反射,没有镜面反射也没有自发光。
- 假设目标表面的面积为 A A A。
- 假设目标表面的漫反射颜色(反照率)为 c d i f f c_{diff} cdiff,即 c d i f f = Φ o u t Φ i n c_{diff} = \frac{\Phi_{out}}{\Phi_{in}} cdiff=ΦinΦout。
接下来本文将根据以上已知信息推导目标 BRDF 函数 f r l a m b e r t i a n ( l , v ) = f r c = ? fr_{lambertian}(l,v)=fr_{c}=? frlambertian(l,v)=frc=?:
2.3.2 推导过程
根据辐射通量/功率(Radiant flux/Power) Φ \Phi Φ 的计算公式
Φ = ∫ Ω L ( w ) ∗ ( n ⋅ w ) d w d A \Phi = \int_{\Omega} L(w)*(n\cdot w) dw\ dA Φ=∫ΩL(w)∗(n⋅w)dw dA
可以得到目标表面的总出射辐射通量 Φ o u t \Phi_{out} Φout 为
Φ o u t = ∫ Ω L o ( v ) ∗ ( n ⋅ v ) d v d A = ∫ 0 2 π ∫ 0 π / 2 L o ( v ) ∗ c o s ( θ ) ∗ s i n ( θ ) d θ d ϕ d A \Phi_{out} = \int_{\Omega} Lo(v)*(n\cdot v) dv\ dA \\ = \int_{0}^{2\pi} \int_{0}^{\pi/2} Lo(v)*cos(\theta)*sin(\theta) d{\theta}d{\phi}\ dA Φout=∫ΩLo(v)∗(n⋅v)dv dA=∫02π∫0π/2Lo(v)∗cos(θ)∗sin(θ)dθdϕ dA
又因为对于 Lambertian 材质,任意出射方向的 L o ( v ) Lo(v) Lo(v) 都相等,并且目标表面的面积为 A A A,因此有:
Φ o u t = ∫ 0 2 π ∫ 0 π / 2 L o ( v ) ∗ c o s ( θ ) ∗ s i n ( θ ) d θ d ϕ d A = ∫ 0 2 π ∫ 0 π / 2 L o c ∗ c o s ( θ ) ∗ s i n ( θ ) d θ d ϕ d A = L o c ∗ ∫ 0 2 π ∫ 0 π / 2 c o s ( θ ) ∗ s i n ( θ ) d θ d ϕ ∗ A = L o c ∗ π ∗ A (7) \Phi_{out} = \int_{0}^{2\pi} \int_{0}^{\pi/2} Lo(v)*cos(\theta)*sin(\theta)\ d{\theta}d{\phi}\ dA \\ = \int_{0}^{2\pi} \int_{0}^{\pi/2} Lo_{c}*cos(\theta)*sin(\theta)\ d{\theta}\ d{\phi}\ dA \\ = Lo_{c} * \int_{0}^{2\pi} \int_{0}^{\pi/2} cos(\theta)*sin(\theta)\ d{\theta}\ d{\phi}\ * A \\ = Lo_{c}*\pi*A \tag{7} Φout=∫02π∫0π/2Lo(v)∗cos(θ)∗sin(θ) dθdϕ dA=∫02π∫0π/2Loc∗cos(θ)∗sin(θ) dθ dϕ dA=Loc∗∫02π∫0π/2cos(θ)∗sin(θ) dθ dϕ ∗A=Loc∗π∗A(7)
那么
L o c = Φ o u t π ∗ A (8) Lo_{c} = \frac{\Phi_{out}}{\pi*A} \tag{8} Loc=π∗AΦout(8)
同理可以得到目标表面的总入射辐射通量 Φ i n \Phi_{in} Φin为:
Φ i n = ∫ Ω L i ( l ) ∗ ( n ⋅ l ) d l d A = ∫ Ω L i ( l ) ∗ ( n ⋅ l ) d l ∗ A (9) \Phi_{in} = \int_{\Omega} Li(l)*(n\cdot l)\ dl\ dA \\ = \int_{\Omega} Li(l)*(n\cdot l)\ dl * A \tag{9} Φin=∫ΩLi(l)∗(n⋅l) dl dA=∫ΩLi(l)∗(n⋅l) dl∗A(9)
那么就有:
Φ i n A = ∫ Ω L i ( l ) ∗ ( n ⋅ l ) d l (10) \frac{\Phi_{in}}{A} = \int_{\Omega} Li(l)*(n\cdot l)\ dl \tag{10} AΦin=∫ΩLi(l)∗(n⋅l) dl(10)
根据渲染方程,我们可以得到:
L o c = L o ( v ) = ∫ Ω f r l a m b e r t i a n ( l , v ) ∗ L i ( l ) ∗ ( n ⋅ l ) d l Lo_{c} = Lo(v) = \int_{\Omega} fr_{lambertian}(l,v)*Li(l)*(n\cdot l)\ dl Loc=Lo(v)=∫Ωfrlambertian(l,v)∗Li(l)∗(n⋅l) dl
因为 f r l a m b e r t i a n ( l , v ) fr_{lambertian}(l,v) frlambertian(l,v) 为定值 f r c fr_{c} frc ,那么就有:
L o c = L o ( v ) = ∫ Ω f r l a m b e r t i a n ( l , v ) ∗ L i ( l ) ∗ ( n ⋅ l ) d l = f r c ∗ ∫ Ω L i ( l ) ∗ ( n ⋅ l ) d l (11) Lo_{c} = Lo(v) = \int_{\Omega} fr_{lambertian}(l,v)*Li(l)*(n\cdot l)\ dl \\ = fr_c * \int_{\Omega} Li(l)*(n\cdot l)\ dl \tag{11} Loc=Lo(v)=∫Ωfrlambertian(l,v)∗Li(l)∗(n⋅l) dl=frc∗∫ΩLi(l)∗(n⋅l) dl(11)
将公式(10)代入公式(11)可以得到:
L o c = L o ( v ) = f r c ∗ ∫ Ω L i ( l ) ∗ ( n ⋅ l ) d l = f r c ∗ Φ i n A (12) Lo_{c} = Lo(v) = fr_c * \int_{\Omega} Li(l)*(n\cdot l)\ dl \\ = fr_c * \frac{\Phi_{in}}{A} \tag{12} Loc=Lo(v)=frc∗∫ΩLi(l)∗(n⋅l) dl=frc∗AΦin(12)
又因为根据公式(8), L o c = Φ o u t / ( π ∗ A ) Lo_{c} = \Phi_{out}/{(\pi*A)} Loc=Φout/(π∗A),那么
L o c = f r c ∗ Φ i n A = Φ o u t π ∗ A (13) Lo_c = fr_c * \frac{\Phi_{in}}{A} = \frac{\Phi_{out}}{\pi*A} \tag{13} Loc=frc∗AΦin=π∗AΦout(13)
又因为 c d i f f = Φ o u t / Φ i n c_{diff} = \Phi_{out}/\Phi_{in} cdiff=Φout/Φin,那么可以得到:
f r c = Φ o u t π ∗ Φ i n = c d i f f π (14) fr_c = \frac{\Phi_{out}}{\pi*\Phi_{in}} = \frac{c_{diff}}{\pi} \tag{14} frc=π∗ΦinΦout=πcdiff(14)
即:
f r L a m b e r t i a n ( l , v ) = f r c = Φ o u t π ∗ Φ i n = c d i f f π (14) fr_{Lambertian}(l,v) = fr_c = \frac{\Phi_{out}}{\pi*\Phi_{in}} = \frac{c_{diff}}{\pi} \tag{14} frLambertian(l,v)=frc=π∗ΦinΦout=πcdiff(14)
至此,我们得到了 Lambertian 材质的 漫反射 BRDF 公式 f r l a m b e r t i a n ( l , v ) = c d i f f π fr_{lambertian}(l,v)=\frac{c_{diff}}{\pi} frlambertian(l,v)=πcdiff.
三、参考引用
[1].Real-Time Rendering, 4th Edition-Chapter 9 Physically Based Shading
[2].Background: Physics and Math of Shading
相关文章:

[OpenGL] Lambertian材质漫反射BRDF方程的解释与推导
一、简介 本文简单的介绍了 Physical Based Rendering, PBR 中的 Lambertian 材质漫反射BRDF公式 f r l a m b e r t i a n c d i f f π fr_{lambertian}\frac{c_{diff}}{\pi} frlambertianπcdiff的推导。 二、漫反射项 根据 渲染方程: L o ( v ) ∫ …...

小火电视桌面TV版下载-小火桌面纯净版下载-官方历史版本安装包
别再费心地寻找小火桌面的官方历史版本安装包啦,试试乐看家桌面吧,它作为纯净版本的第三方桌面,具有诸多优点。 界面简洁纯净:乐看家桌面设计简洁流畅,页面简洁、纯净无广告,为用户打造了一个干净的电视操…...
)
VSFTPD+虚拟用户+SSL/TLS部署安装全过程(踩坑全通)
Author : Spinach | GHB Link : http://blog.csdn.net/bocai8058文章目录 前言准备配置虚拟用户1.创建虚拟用户列表文件2.生成数据库文件3.设置虚拟用户独立访问权限 配置PAM认证1.创建PAM配置文件2.测试PAM认证 创建虚拟用户映射的系统用户生成SSL/TLS证书配置VSFTPD服务1…...

07 Python 字符串全解析
文章目录 一. 字符串的定义二. 字符串的基本用法1. 访问字符串中的字符2. 字符串切片3. 字符串拼接4. 字符串重复5.字符串比较6.字符串成员运算 三. 字符串的常用方法1. len() 函数2. upper() 和 lower() 方法3. strip() 方法4. replace() 方法5. split() 方法 四. 字符串的进阶…...

androidstudio安装配置
B站配置视频AndroidStudio安装配置教程(最新版本教程)3分钟搞定 快速安装使用_哔哩哔哩_bilibili 1、环境变量 D:\AndroidSdk ANDROID_HOME ANDROID_SDK_HOME 2、新建 3、配置 distributionUrlhttps://mirrors.cloud.tencent.com/gradle/gradle-8.11.1-…...
:AI 大模型的“万能连接器”)
全面解析 MCP(Model Context Protocol):AI 大模型的“万能连接器”
一、MCP 的定义与技术定位 **MCP(Model Context Protocol,模型上下文协议)**是由 Anthropic 公司于 2024 年 11 月推出的开源协议,旨在为 AI 大模型与外部数据源、工具之间建立标准化连接通道。它被业界称为 “AI 的 USB-C 接口”,通过统一的通信协议和数据结构,解决大模…...

《AI大模型趣味实战》基于RAG向量数据库的知识库AI问答助手设计与实现
基于RAG向量数据库的知识库AI问答助手设计与实现 引言 随着大语言模型(LLM)技术的快速发展,构建本地知识库AI问答助手已成为许多企业级应用的需求。本研究报告将详细介绍如何基于FLASK开发一个使用本地OLLAMA大模型底座的知识库AI问答助手&…...

Lua 第8部分 补充知识
8.1 局部变量和代码块 Lua 语言中的变量在默认情况下是全局变量 ,所有的局部变量在使用前必须声明 。 与全局变量不同,局部变量的生效范围仅限于声明它的代码块。一个代码块( block )是一个控制结构的主体,或是一个函…...

正则表达式三剑客之——awk命令
目录 一.什么是awk 二.awk的语法格式 1.选项 2. 模式(Pattern) 3. 操作(Action) 4. 输入文件(file) 5.总结 三.awk的工作原理 1. 逐行扫描输入 2. 匹配模式 1.正则表达式: 2.逻辑…...

BeeWorks Meet:私有化部署视频会议的高效选择
在数字化时代,视频会议已成为企业沟通协作的重要工具。然而,对于金融、政务、医疗等对数据安全和隐私保护要求极高的行业来说,传统的公有云视频会议解决方案往往难以满足其严格的安全标准。此时,BeeWorks Meet 私有化部署视频会议…...

[Mybatis-plus]
简介 MyBatis-Plus (简称 MP)是一个 MyBatis的增强工具,在 MyBatis 的基础上只做增强不做改变。Mybatis-plus官网地址 注意,在引入了mybatis-plus之后,不要再额外引入mybatis和mybatis-spring,避免因为版本…...

IPv6 技术细节 | 源 IP 地址选择 / Anycast / 地址自动配置 / 地址聚类分配
注:本文为 “IPv6 技术细节” 相关文章合集。 部分文章中提到的其他文章,一并引入。 略作重排,未整理去重。 如有内容异常,请看原文。 闲谈 IPv6 - 典型特征的一些技术细节 iteye_21199 于 2012-11-10 20:54:00 发布 0. 巨大的…...

【高频考点精讲】ES6 String的新增方法,处理字符串更方便了
ES6 String的新增方法:处理字符串从未如此优雅 【初级】前端开发工程师面试100题(一) 【初级】前端开发工程师面试100题(二) 【初级】前端开发工程师的面试100题(速记版) 作为天天和字符串打交道的码农,谁还没被indexOf和substring折磨过?ES6给String对象新增的几个方…...

【工具】使用 MCP Inspector 调试服务的完全指南
Model Context Protocol (MCP) Inspector 是一个交互式开发工具,专为测试和调试 MCP 服务器而设计。本文将详细介绍如何使用 Inspector 工具有效地调试和测试 MCP 服务。 1. MCP Inspector 简介 MCP Inspector 提供了直观的界面,让开发者能够ÿ…...

【音视频】AVIO输入模式
内存IO模式 AVIOContext *avio_alloc_context( unsigned char *buffer, int buffer_size, int write_flag, void *opaque, int (*read_packet)(void *opaque, uint8_t *buf, int buf_size), int (*write_packet)(void *opaque, uint8_t *buf, int buf_size), int64_t (*seek)(…...

AI与思维模型【76】——SWOT思维模型
一、定义 SWOT思维模型是一种用于分析事物内部和外部因素的战略规划工具。其中,S代表优势(Strengths),是指事物自身所具备的独特能力、资源或特点,这些因素有助于其在竞争中取得优势;W代表劣势(…...

大模型提示词如何编写
一、提示词的核心三要素 明确目标(What) 告诉 AI「你要它做什么」,越具体越好。 ❌ 模糊:写一篇文章 ✅ 清晰:写一篇 800 字的高考作文,主题 “坚持与创新”,结构分引言、三个论点(…...

python如何取消word中的缩进
在python-docx中,取消缩进可以通过将相应的缩进属性设置为None或0来实现。以下是取消不同类型缩进的方法: 取消左缩进 from docx import Documentdoc Document(existing_document.docx)for paragraph in doc.paragraphs:# 取消左缩进paragraph.paragr…...

DDL小练习
1.创建一张t_user表 要求属性有id(INT),name(VARCHAR),sex(VARCHAR),birthday(DATE) 其中id和name不能为空,添加数据并测试。 创建数据库 create database spt2503; 创建数据库中的t_user表 create table t_user (id int not null, name varchar(20) not…...
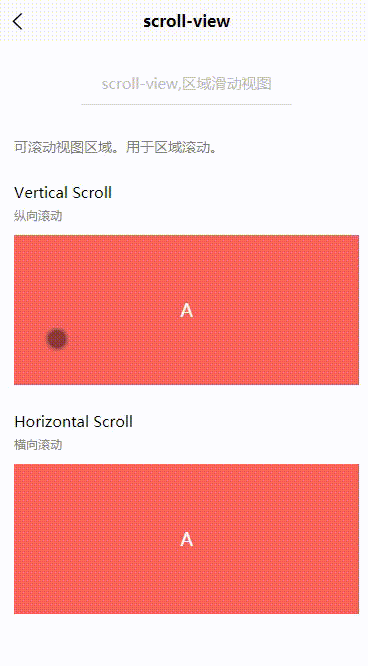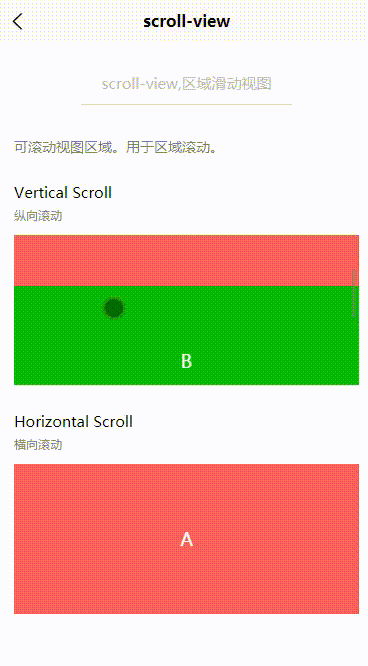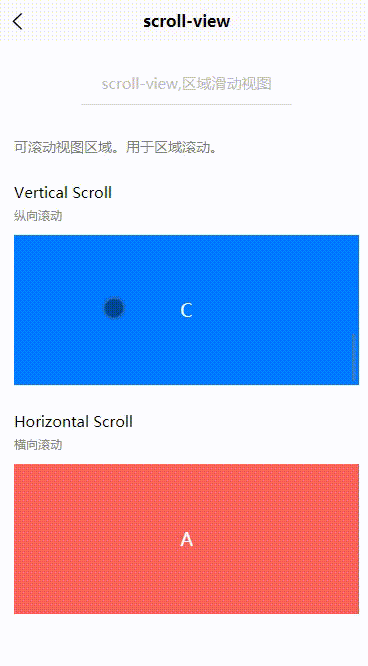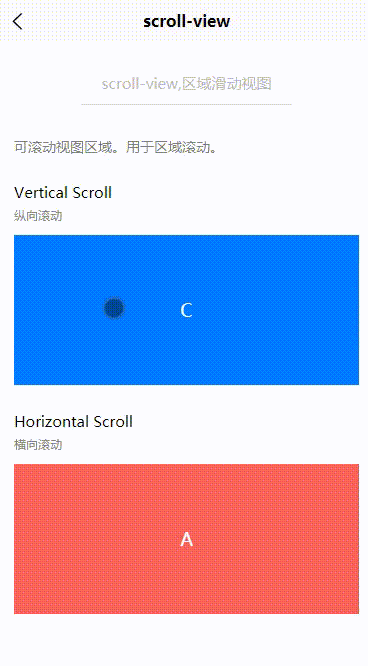
Uniapp:scroll-view(区域滑动视图)
目录 一、基本概述二、属性说明三、基本使用3.1 纵向滚动3.2 横向滚动一、基本概述 scroll-view,可滚动视图区域。用于区域滚动。 二、属性说明 属性名类型默认值说明平台差异说明scroll-xBooleanfalse允许横向滚动scroll-yBooleanfalse允许纵向滚动三、基本使用 3.1 纵向滚…...

【前端】【面试】在前端开发中,如何实现图片的渐进式加载,以及这样做的好处是什么?
题目:在前端开发中,如何实现图片的渐进式加载,以及这样做的好处是什么? 在浏览器端实现图片的“渐进式加载”(Progressive Image Loading)常用的三种方式 方法思路典型实现要点适用场景优缺点简述1. 使…...

单精度浮点运算/定点运算下 MATLAB (VS) VIVADO
VIVADO中单精度浮点数IP核计算结果与MATLAB单精度浮点数计算结果的对比 MATLAB定点运算仿真,对比VIVADO计算的结果 目录 前言 一、VIVADO与MATLAB单精度浮点数运算结果对比 二、MATLAB定点运算仿真 总结 前言 本文介绍了怎么在MATLAB中使用单精度浮点数进行运算…...

基于大模型对先天性巨结肠全流程预测及医疗方案研究报告
目录 一、引言 1.1 研究背景与意义 1.2 研究目的与创新点 二、大模型在先天性巨结肠预测中的理论基础 2.1 大模型概述 2.2 大模型预测先天性巨结肠的可行性分析 三、术前预测与准备方案 3.1 大模型对术前病情的预测 3.1.1 疾病确诊预测 3.1.2 病情严重程度评估 3.2 …...

【AI插件开发】Notepad++ AI插件开发1.0发布和使用说明
一、产品简介 AiCoder是一款为Notepad设计的轻量级AI辅助插件,提供以下核心功能: 嵌入式提问:对选中的文本内容进行AI分析,通过侧边栏聊天界面与AI交互,实现多轮对话、问题解答或代码生成。对话式提问:独…...

【MySQL数据库入门到精通-07 函数-字符串函数、数值函数、日期函数和流程函数】
文章目录 一、字符串函数1. MySQL中的函数主要分为以下四类: 字符串函数、数值函数、日期函数、流程函数。下面是字符串函数常见的函数,见下表。2.具体代码实现3.结果 二、数值函数1.知识点2.具体代码实现3.结果 三、日期函数1.知识点2.具体代码实现3.结…...

Python图像处理——基于Retinex算法的低光照图像增强系统
1.项目内容 (1)算法介绍 ①MSRCR (Multi-Scale Retinex with Color Restoration) MSRCR 是多尺度 Retinex 算法(MSR)的扩展版,引入了色彩恢复机制以进一步提升图像增强质量。MSR 能有效地压缩图像动态范围ÿ…...

如何在JDK17项目中改成1.8
1.调整 Spring Boot 版本 由于 Spring Boot 3.x 最低要求 JDK 17,所以如果要使用 JDK 8,需要把 spring-boot-starter-parent 的版本降低到 2.7.x 系列,这个系列是支持 JDK 8 的。示例如下: <parent><groupId>org.sp…...

【不同名字的yolo的yaml文件名是什么意思】
以下是这些 YOLO 系列配置文件的详细解析,按版本和功能分类说明: 一、YOLOv3 系列 文件名核心特性适用场景yolov3.yaml原始 YOLOv3 结构,3 尺度预测(13x13,26x26,52x52)通用目标检测yolov3-spp.yaml增加 SPPÿ…...

Zephyr kernel Build System (CMake)介绍
目录 概述 1. 结构介绍 2 构建和配置阶段 2.1 配置阶段 2.2 Cmake编译 3 Zephy项目目录结构 3.1 文件架构 3.2 文件content 概述 本文主要介绍Zephyr kernel Build System CMake的功能,以及使用该工具构建项目,并详细介绍了每个目录以及目录下文…...

相对论大师-记录型正负性质BFS/图论-链表/数据结构
看到这一题我的第一个思路就是双向bfs 起点是a,终点还是a,但是flag是相反的(“越”的方向) tip1.可以用字典vis来存储flag 刚开始初始化时vissta,visend一个对应0、1 要求两个队列相…...
