Day12(回溯法)——LeetCode51.N皇后39.组合总和
1 前言
今天刷了三道回溯法和一道每日推荐,三道回溯法也迷迷糊糊的,每日推荐把自己绕进去了,虽然是一道之前做过的题的变种。刷的脑子疼。。。今天挑两道回溯题写一下吧,其中有一道是之前做过的N皇后,今天在详细写一写。
2 LeetCode51.N皇后(LeetCode)
2.1 题目描述
题目描述如下:

示例如下:

2.2 题目分析及解决
思路大概就是从第一行的第一列开始放置皇后,然后递归下一行,直到找到第一个皇后在第一行第一列的所有解,然后回溯到第一行,进行第二列的搜索。
这里用vector<string> path记录每个解,定义queue(int row,int n)来找第row行合法的皇后位置,n是总行数。当我们找到第n行时,且能找到解,则将该结果保存到答案中,然后返回,寻求其他解。
尝试把皇后放在该行的每一列中,若与之前的皇后放置位置没有冲突,则放置皇后。这里就发现,我们需要一个数组来保存之前皇后放置的位置。设state[i]=j,表示第i行皇后放在第j列,因此每次放置皇后,都只需要检验其与之前的行的皇后有无矛盾即可,将在同一列,对角线以及反对角线的情况写出来,观察下标可以很容易进行判断:
bool conflict(int r,int j){for(int i=0;i<r;i++){if(state[i]==j||(abs(state[i]-j)==abs(r-i))){return true;}}return false;}
当递归找下一行后,需要在其递归返回后恢复现场,即将state和path恢复原始状态。
完整代码如下:
#include<string>
#include<vector>
class Solution {
public:vector<vector<string>> ans;vector<string> path;vector<int> state;bool conflict(int r,int j){for(int i=0;i<r;i++){if(state[i]==j||(abs(state[i]-j)==abs(r-i))){return true;}}return false;}void queue(int row,int n){if(row==n){ans.push_back(path);return;}for(int j=0;j<n;j++){if(!conflict(row,j)){//记录当前行皇后的位置state[row]=j;//放置皇后path[row][j]='Q';queue(row+1,n);//回溯path[row][j]='.';state[row]=-1;}}}vector<vector<string>> solveNQueens(int n) {path=vector<string>(n,string(n,'.'));state=vector<int>(n,-1);queue(0,n);return ans;}
};
3 LeetCode39.组合总和(LeetCode39)
3.1 题目描述
题目描述如下:

具体实例如下:

3.2 题目分析及解决
感觉好像是重复背包问题(有点记不清了)。思路大概都好想,假设现在判断是否使用第i个数,若使用nums[i]后,其仍没超过target,则可以继续从第i个数进行递归(即再次判断能否使用nums[i]);若超过了target,则需要尝试使用别的数,若其余数都不符合,则回溯到第i个数前,尝试使用别的数。这里注意到,如果我们提前将数组进行排序,则当使用nums[i]后超过target后,则nums[i]后面的数也一定不能使用,从而提前结束递归(剪枝)。
具体代码如下:
class Solution {
public:vector<vector<int>> ans;vector<int> path;void dfs(vector<int>& candidates,int target,int i){//找到正确解,放入结果if(target==0){ans.push_back(path);return;}//若当前和大于target,返回,递归会尝试放下一个元素if(target<0) return;for(int start=i;start<candidates.size();start++){//不断放入第i个元素if(target-candidates[start]>=0){path.push_back(candidates[start]);//递归处理,可重复使用元素,因此下一次开始仍然是startdfs(candidates,target-candidates[start],start);//回溯,移除当前解,尝试其他可能//target隐式的回溯,因为其是函数变量path.pop_back();}}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());dfs(candidates,target,0);return ans;}
};
4 感想
想理解回溯,感觉重要的是理解递归,递归猛一看感觉还不错,但是当其在语句中运行时,往往分不清什么时候运行哪一句,什么时候运行下一句,返回时哪些变量恢复到递归前的值,哪些变量需要自己手动回溯等等。
还需要自己手动画一下递归树,以及剪枝的过程,回溯的过程。此外在设计函数时也需要仔细思考,好的函数往往能事半功倍。总之自己对回溯对递归理解的还远远不够。。。真的头大。。。
相关文章:

Day12(回溯法)——LeetCode51.N皇后39.组合总和
1 前言 今天刷了三道回溯法和一道每日推荐,三道回溯法也迷迷糊糊的,每日推荐把自己绕进去了,虽然是一道之前做过的题的变种。刷的脑子疼。。。今天挑两道回溯题写一下吧,其中有一道是之前做过的N皇后,今天在详细写一写…...

简历中的专业技能
Java 精通Java 核心,多年一线研发经验,具备良好的编码能力、并熟练应用设计模式精通多进程、Java 高并发编程,阅读过相关 JDK 源码以及Lock锁的底层源码,熟悉 AQS 和 CAS 的核心思想,能够运用其机制优化并发编程精通 …...
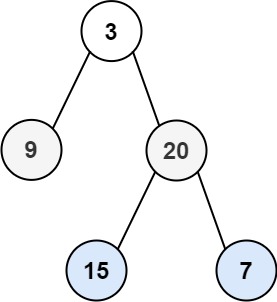
力扣HOT100——102.二叉树层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]] /*** Definition for a bi…...

【Token系列】05 | 位置编码不是位置信息:Transformer如何建立语言顺序感?
文章目录 05 | 位置编码不是位置信息:Transformer如何建立语言顺序感?一、为什么Transformer需要“位置感知”?二、什么是位置编码(Position Encoding, PE)?三、相对 vs 绝对位置编码四、可学习位置编码机制…...

springboot启动的端口如何终止
若要终止 Spring Boot 应用所使用的端口,可依据应用的运行方式,采用不同的解决办法。以下为你详细介绍: 1. 直接停止正在运行的 Spring Boot 应用程序 开发环境(IDE 中运行) IntelliJ IDEA:在 IDE 的运行…...
)
chrony服务器(1)
简介 NTP NTP(Network Time Protocol,网络时间协议)是一种用于同步计算机系统时间的协议是TCP/IP协议族中的一个应用层协议,主要用于在分布式时间服务器和客户端之间进行时钟同步,提供高精准度的时间校正通过分层的时…...

搭建基于火灾风险预测与防范的消防安全科普小程序
基于微信小程序的消防安全科普互动平台的设计与实现,是关于微信小程序的,知识课程学习,包括学习后答题。 技术栈主要采用微信小程序云开发,有下面的模块: 1.课程学习模块 2.资讯模块 3.答题模块 4.我的模块 还需…...

RAG技术与应用---0426
大语言模型>3.10 课程中会用到python 工具箱: faiss,modelscope,langchain,langchain_community,PyPDF2 1)大模型应用开发的三种模式 提示词没多少工作量,微调又花费时间费用,RAG是很多公司招聘用来对LLM进行应用…...

element-ui多个form同时验证,以及动态循环表单注意事项
多个form同时验证: validateForm(refs) {if (!refs) {return false}return new Promise((resolve, reject) > {refs.validate().then((valid) > {resolve(valid)}).catch((val) > {resolve(false)})}) }, async handleConfirm() {Promise.all([this.valid…...

k8s学习记录(四):节点亲和性
一、前言 在上一篇文章里,我们了解了 Pod 中的nodeName和nodeSelector这两个属性,通过它们能够指定 Pod 调度到哪个 Node 上。今天,我们将进一步深入探索 Pod 相关知识。这部分内容不仅信息量较大,理解起来也有一定难度࿰…...

文本预处理(NLTK)
1. 自然语言处理基础概念 1.1 什么是自然语言处理 自然语言处理( Natural Language Processing, NLP)是计算机科学领域与人工智能领域中的一个重要方向。它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。自然语言处理是一门融语言学、计算机科学、数学于…...

一些常见的资源池管理、分布式管理和负载均衡的监控工具
资源池管理监控工具 Prometheus 是一款开源的系统监控和警报工具。它可以通过收集各种指标数据,如CPU使用率、内存使用量、磁盘I/O等,来监控资源池中的服务器、容器等资源。Prometheus具有强大的查询语言和可视化功能,能够帮助管理员快速了解资源的使用情况,并及时发现潜在…...

Neo4j 可观测性最佳实践
Neo4j 介绍 Neo4j 是一款领先的图数据库管理系统,采用图数据模型来表示和存储数据。它以节点、关系和属性的形式组织数据,节点代表实体,关系表示节点间的连接,属性则为节点和关系附加信息。Neo4j 使用 Cypher 查询语言࿰…...

JAVA服务内存缓慢上涨,年轻代GC正常但Full GC频繁,如何定位?
1. 分析 : 年轻代GC正常,说明年轻代的对象回收没有问题,可能大部分对象都是朝生夕死的,所以Minor GC能有效清理。但Full GC频繁,通常意味着老年代空间不足,导致频繁进行Full GC来回收老年代。而内存缓慢上…...
)
C++入门(讲解1)
1. namespace的定义 1.1 定义命名空间,需要用到namespace关键字,后面跟命名空间的名字,然后接一对{}即可,{}中就是命名空间的成员。命名空间中可以定义变量/函数/类型等。 1.2 namespace的本质是定义出一个域,这个…...

react的ant-design-pro框架左侧菜单修改为动态路由
在使用 React 框架结合 Ant Design Pro 进行项目开发时,动态路由的修改是一项常见且重要的任务。动态路由能够根据用户的角色、权限或者其他运行时的条件来展示不同的页面内容,极大地提升了应用的灵活性和安全性。本文将结合一个完整的示例项目ÿ…...

【教程】Windows通过网线共享网络给其它设备
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 1、打开“控制面板”。 2、点击“网络和共享中心”。 3、点击“更改适配器设置”。 4、选中要共享的网络适配器,右击选中“属性”。 5、勾选…...
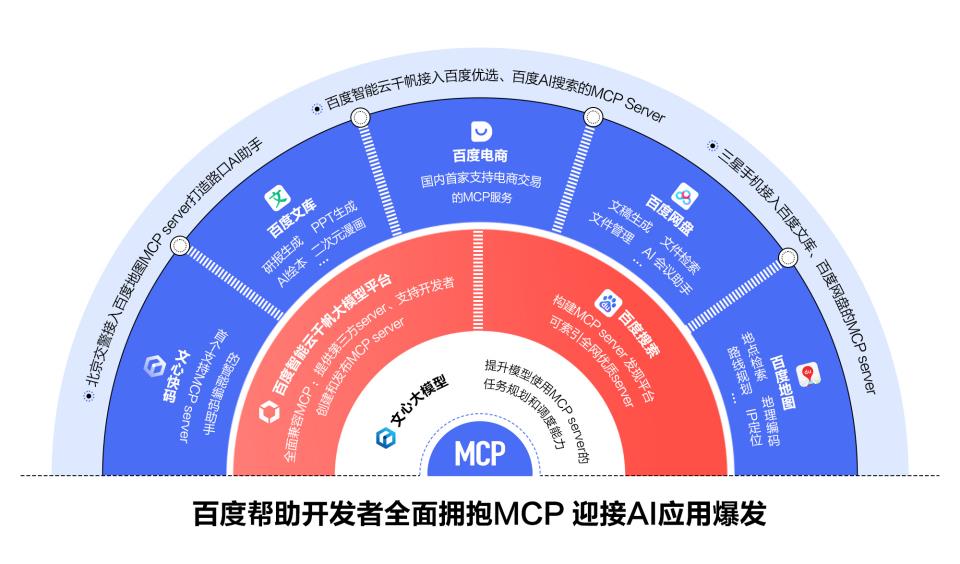
百度AI开发者大会:连发多款AI应用,覆盖AI数字人等热门赛道
4月25日,Create2025百度AI开发者大会在武汉隆重举办。百度创始人李彦宏发表了题为《模型的世界 应用的天下》的演讲。60分钟的演讲中,李彦宏发布了两大模型,多款热门AI应用,并宣布将帮助开发者全面拥抱MCP。 当天发布的文心大模型…...

Java 线程的六种状态与完整生命周期详解
🚀 Java 线程的几种状态详解 在 Java 中,线程状态(Thread State)是由 Thread.State 枚举定义的,总共有六种: 状态含义典型场景示例NEW新建状态,线程对象刚创建,还未调用 start() 方…...

05--Altium Designer(AD)的详细安装
一、软件的下载 Altium Designer官网下载 1、临近五一的假期,想着搞个项目,且这个项目与PCB有关系,所以就下这个软件来玩玩。下面保姆级教大家安装。 2、选择适合自己的版本下载(我安装的是24的) 3、软件安装 1.下…...

2:QT联合HALCON编程—图像显示放大缩小
1.声明事件 #include <HalconCpp.h> using namespace HalconCpp;#include <QCloseEvent>//滚轮事件 2.在.h文件中声明和定义公共全局变量,以及图像缩放的函数 void wheelEvent(QWheelEvent *event);//定义函数HTuple wcRow0, wcRow1, wcCol0, wcCol1,m…...

Java 队列与阻塞队列全面解析:从 Queue 到 TransferQueue 的实现与应用
文章目录 Queue队列QueueDeque 阻塞队列BlockingQueueArrayBlockingQueueLinkedBlockingQueuePriorityBlockingQueueSynchronousQueueDelayQueue BlockingDequeLinkedBlockingDeque TransferQueueLinkedTransferQueue Queue Queue(队列)是一种特殊的线性…...

服务器虚拟化:技术解析与实践指南
在信息技术飞速发展的今天,企业对服务器资源的需求日益增长,传统物理服务器存在资源利用率低、部署周期长、管理成本高等问题。服务器虚拟化技术应运而生,它通过将物理服务器的计算、存储、网络等资源进行抽象和整合,划分成多个相互隔离的虚拟服务器,从而提高资源利用率、…...

【蓝桥杯省赛真题56】Scratch抓不住的蜜蜂 蓝桥杯scratch图形化编程 中小学生蓝桥杯省赛真题讲解
目录 scratch抓不住的蜜蜂 一、题目要求 1、准备工作 2、功能实现 二、案例分析 1、角色分析 2、背景分析 3、前期准备 三、解题思路 四、程序编写 五、考点分析 六、推荐资料 1、scratch资料 2、python资料 3、C++资料 scratch抓不住的蜜蜂 第十五届青少年蓝桥…...
:深入剖析synchronized关键字的底层原理)
线程池(二):深入剖析synchronized关键字的底层原理
线程池(二):深入剖析synchronized关键字的底层原理 线程池(二):深入剖析synchronized关键字的底层原理一、基本使用1.1 修饰实例方法1.2 修饰静态方法1.3 修饰代码块 二、Monitor2.1 Monitor的概念2.2 Moni…...

【线段树】P8539 「Wdoi-2」来自地上的支援|普及+
P8539 「Wdoi-2」来自地上的支援 题目背景 波光粼粼的山顶湖与庄严神圣的神社之下,是一座复合型活火山。 沿幻想风穴而下,便能到达火山之下,废弃已久的地狱原址。 在旧地狱中,有一座大都市。那里是旧地狱还是地狱的时候在那工作…...

《TCP/IP详解 卷1:协议》之第七、八章:Ping Traceroute
目录 一、ICMP回显请求和回显应答 1、ICMP回显请求 2、ICMP回显应答 二、ARP高速缓存 三、IP记录路由选项(Record Route,RR) 1、记录路由选项的工作过程 2、RR 选项的 IP 头部格式 2.1、RR 请求 2.2、RR响应 四、ping 的去返路径 五…...

Leetcode:1. 两数之和
题目 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。 你可以按任意顺序返回答案。 示…...

【Java学习笔记】冒泡排序
冒泡排序 思想:经过一轮遍历比较,把最大的放在数组的末尾 int[] a {3, 2, 1}; for( int i 0; i < a.length-1; i){for( int j 0; j < a.length-1-i; j){if(a[j] > a[j1]){int temp a[j];a[j] a[j1];a[j1] temp;}} } for( int i 0; i &…...
)
【数字图像处理】立体视觉基础(2)
相机标定 【1】相机标定的概念 相机参数:相机成像的几何模型的参数 相机标定:求解参数的过程 【2】相机标定的作用 (1)求出相机的内、外参数,以及畸变参数 (2)校正镜头畸变影响,…...
