高中数学联赛模拟试题精选第18套几何题
在 △ A B C \triangle ABC △ABC 中, A B < A C AB< AC AB<AC, 点 K K K, L L L, M M M 分别是边 B C BC BC, C A C A CA, A B AB AB 的中点. △ A B C \triangle ABC △ABC 的内切圆圆心为 I I I, 且与边 B C BC BC 相切于点 D D D. 直线 l l l 经过线段 I D ID ID 的中点且与 I K IK IK 垂直, 与直线 L M LM LM 交于点 P P P. 证明: ∠ P I A = 9 0 ∘ \angle P I A = 90^{\circ} ∠PIA=90∘.
(《高中数学联赛模拟试题精选》第18套)
证明:

设 l l l 交 I D ID ID 于点 T T T, 交 I K IK IK 于点 Q Q Q, 延长 D I DI DI 交 M L ML ML 于点 R R R.
显然 R R R, P P P, Q Q Q, I I I 四点共圆且 P I PI PI 为直径.
要证明 ∠ P I A = π 2 \angle PIA=\frac{\pi}{2} ∠PIA=2π, 只需证明 A I AI AI 切 ( R P Q ) (RPQ) (RPQ) 于点 I I I, 这等价于证明 ∠ R Q I = ∠ R I A \angle RQI=\angle RIA ∠RQI=∠RIA.

延长 D I DI DI 交内切圆于点 S S S. 设过 S S S 的 B C BC BC 的平行线分别交 A B AB AB, A C AC AC 于点 B ′ B' B′, C ′ C' C′. 设 A A A 在 B ′ C ′ B'C' B′C′ 和 B C BC BC 上的投影分别为点 H ′ H' H′, H H H. 设 D ′ D' D′ 为 ∠ B A C \angle BAC ∠BAC 内的旁切圆在 B C BC BC 上的切点.
显然 ∠ B ′ A C ′ ∼ △ A B C \angle B'AC' \sim \triangle ABC ∠B′AC′∼△ABC, ⊙ I \odot I ⊙I 是 △ A B ′ C ′ \triangle AB'C' △AB′C′ 的旁切圆, S S S 是其在 B ′ C ′ B'C' B′C′ 上的切点. 由此易知 S S S 和 D ′ D' D′ 是对应点, 进而可知 A A A, S S S, D ′ D' D′ 共线.
显然 I K / / S D ′ IK//SD' IK//SD′, 所以 ∠ D S D ′ = ∠ D I K \angle DSD'=\angle DIK ∠DSD′=∠DIK.
A S / I S = A S A H ′ A H ′ I S AS/IS = \frac{AS}{AH'} \frac{AH'}{IS} AS/IS=AH′ASISAH′.
I R / I Q = I R I T I T I Q IR/IQ = \frac{IR}{IT} \frac{IT}{IQ} IR/IQ=ITIRIQIT.
易知 A S A H ′ = I T I Q \frac{AS}{AH'} = \frac{IT}{IQ} AH′AS=IQIT.
A S A D ′ = A H ′ A H \frac{AS}{AD'} = \frac{AH'}{AH} AD′AS=AHAH′
I R I T = 1 2 A H − I D 1 2 I D = A H − 2 I D I D \frac{IR}{IT} = \frac{\frac{1}{2}AH-ID}{\frac{1}{2}ID}=\frac{AH-2ID}{ID} ITIR=21ID21AH−ID=IDAH−2ID
A H ′ I S = A H − 2 I D I D = I R I T \frac{AH'}{IS} = \frac{AH-2ID}{ID} = \frac{IR}{IT} ISAH′=IDAH−2ID=ITIR.
综上, △ A S I ∼ △ R I Q \triangle ASI \sim \triangle RIQ △ASI∼△RIQ. 由此可知 ∠ A I S = ∠ R Q I \angle AIS=\angle RQI ∠AIS=∠RQI.
证毕.
相关文章:

高中数学联赛模拟试题精选第18套几何题
在 △ A B C \triangle ABC △ABC 中, A B < A C AB< AC AB<AC, 点 K K K, L L L, M M M 分别是边 B C BC BC, C A C A CA, A B AB AB 的中点. △ A B C \triangle ABC △ABC 的内切圆圆心为 I I I, 且与边 B C BC BC 相切于点 D D D. 直线 l l l 经过线段…...

Kettle学习
一、Kettle 简介 Kettle(现称为 Pentaho Data Integration)是一款开源ETL工具,支持从多种数据源抽取、转换和加载数据,广泛应用于数据仓库构建、数据迁移和清洗。其核心优势包括: 可视化操作:通过拖拽组件设计数据处理流程(转换和作业)。多数据源支持:数据库(MySQL/…...

Synopsys 逻辑综合的整体架构概览
目录 一、DC Shell 逻辑综合的整体架构概览 ⛓️ 逻辑综合的主要阶段(Pipeline) 二、核心架构模块详解 1. Internal Database(设计对象数据库) 2. Scheduler(调度器) 3. Rewriting Engine(…...

Missashe考研日记-day27
Missashe考研日记-day27 0 写在前面 博主昨晚有事所以没学专业课,白天学了其他科,但是觉得不太好写博客,就合在今天一起写好了。 1 专业课408 学习时间:3h30min学习内容: 今天把内存管理部分剩下的关于分页分段和段…...

Java 富文本转word
前言: 本文的目的是将传入的富文本内容(html标签,图片)并且分页导出为word文档。 所使用的为docx4j 一、依赖导入 <!-- 富文本转word --><dependency><groupId>org.docx4j</groupId><artifactId>docx4j</artifactId&…...

多模态大语言模型arxiv论文略读(四十三)
InteraRec: Screenshot Based Recommendations Using Multimodal Large Language Models ➡️ 论文标题:InteraRec: Screenshot Based Recommendations Using Multimodal Large Language Models ➡️ 论文作者:Saketh Reddy Karra, Theja Tulabandhula …...
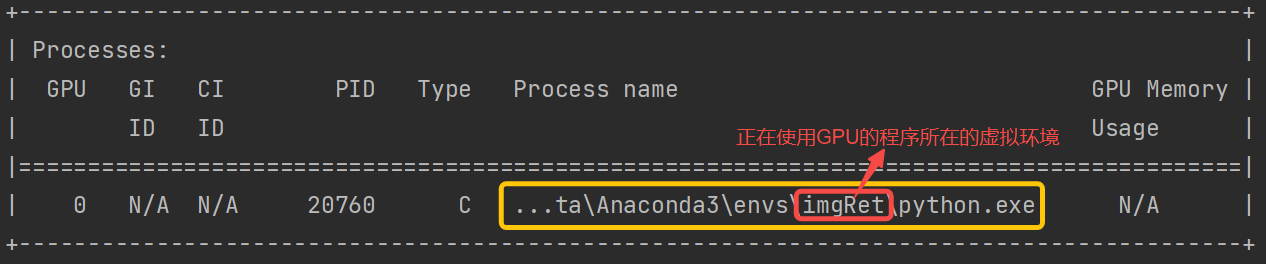
GPU加速-系统CUDA12.5-Windows10
误区注意 查看当前系统可支持的最高版本cuda:nvidia-smi 说明: 此处显示的12.7只是驱动对应的最高版本,不一定是 / 也不一定需要是 当前Python使用的版本。但我们所安装的CUDA版本需要 小于等于它(即≤12.7)因此即使…...

kafka课后总结
Kafka是由LinkedIn开发的分布式发布 - 订阅消息系统,具备高吞吐量、低延迟、可扩展性、持久性、可靠性、容错性和高并发等特性。其主要角色包括Broker、Topic、Partition、Producer、Consumer、Consumer Group、replica、leader、follower和controller。消息系统中存…...
)
排序算法(快排+推排序+归并排序)
一、快排(不稳定O(NlogN)) 分治思想,随机选一个数作为pivot,然后放到数组最后去,比这个元素小的放左边,比这个元素大的放右边。最后再交换左边放完后的下一个元素和pivot,这样就把一个元素排好…...

【股票系统】使用docker本地构建ai-hedge-fund项目,模拟大师炒股进行分析。人工智能的对冲基金的开源项目
股票系统: https://github.com/virattt/ai-hedge-fund 镜像地址: https://gitcode.com/gh_mirrors/ai/ai-hedge-fund 项目地址: https://gitee.com/pythonstock/docker-run-ai-hedge-fund 这是一个基于人工智能的对冲基金的原理验证项目。本项目旨在探讨利用人工智能进行…...

施工安全巡检二维码制作
进入新时代以来,人们对安全的重视程度越来越高。特别在建筑施工行业,安全不仅是关乎着工人的性命,更是承载着工人背后家庭的幸福生活。此时就诞生了安全巡检的工作,而巡检过程中内容庞杂,安全生产检查、隐患排查、施工…...
**、**增广律(Augmentation)** 和 **传递律(Transitivity)?)
什么是函数依赖中的 **自反律(Reflexivity)**、**增广律(Augmentation)** 和 **传递律(Transitivity)?
文章目录 1. 自反律(Reflexivity Rule)规则定义实际例子应用意义 2. 增广律(Augmentation Rule)规则定义实际例子应用意义 3. 传递律(Transitivity Rule)规则定义实际例子应用意义 综合应用场景:…...

基于 Google Earth Engine (GEE) 的土地利用变化监测
一、引言 土地利用变化是全球环境变化的重要组成部分,对生态系统、气候和人类社会产生深远影响。利用遥感技术可以快速、准确地获取土地利用信息,监测其变化情况。本文将详细介绍如何使用 GEE 对特定区域的 Landsat 影像进行处理,实现土地利…...

Java基础语法10分钟速成
Java基础语法10分钟速成,记笔记版 JDKhello world变量字符串 类,继承,多态,重载 JDK JDK即Java development key,Java环境依赖包 在jdk中 编译器javac将代码的Java源文件编译为字节码文件(.classÿ…...

如何在Spring Boot中实现热加载以避免重启服务器
在 Spring Boot 开发中,频繁修改代码(如 Java 类、配置文件或静态资源)通常需要重启服务器,这会中断开发流程并降低效率。热加载(Hot Reloading)允许开发者在不重启服务器的情况下重新加载更改,…...
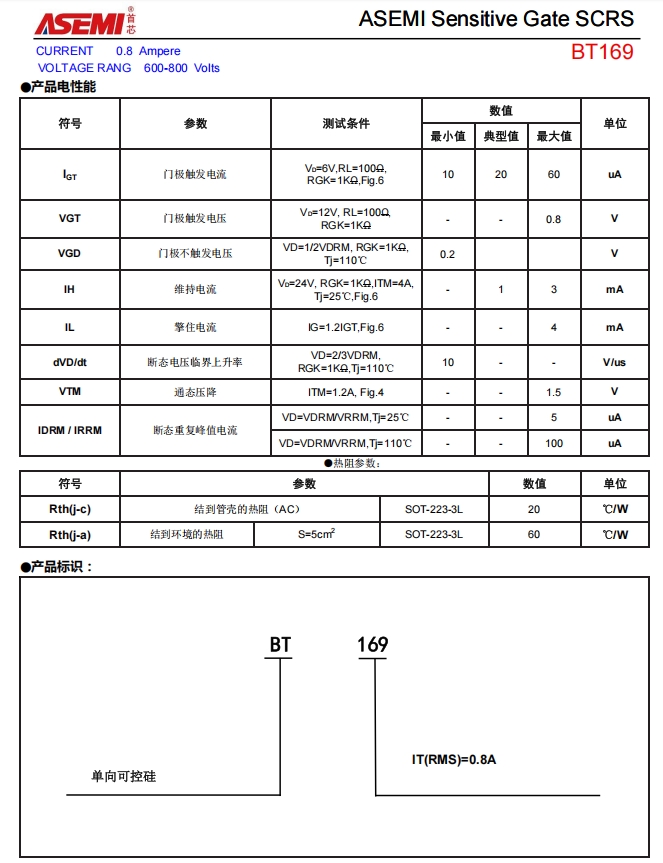
BT169-ASEMI无人机专用功率器件BT169
编辑:ll BT169-ASEMI无人机专用功率器件BT169 型号:BT169 品牌:ASEMI 封装:SOT-23 批号:最新 引脚数量:3 特性:单向可控硅 工作温度:-40℃~150℃ BT169单向可控硅ÿ…...
——STL之排序算法)
C++学习笔记(三十六)——STL之排序算法
一、STL 算法 C的STL(Standard Template Library) 提供了一组高效、通用的算法,这些算法适用于各种容器(如 vector、list、set、map)。 这些算法主要位于 <algorithm> 和 <numeric> 头文件中。 通用性&a…...
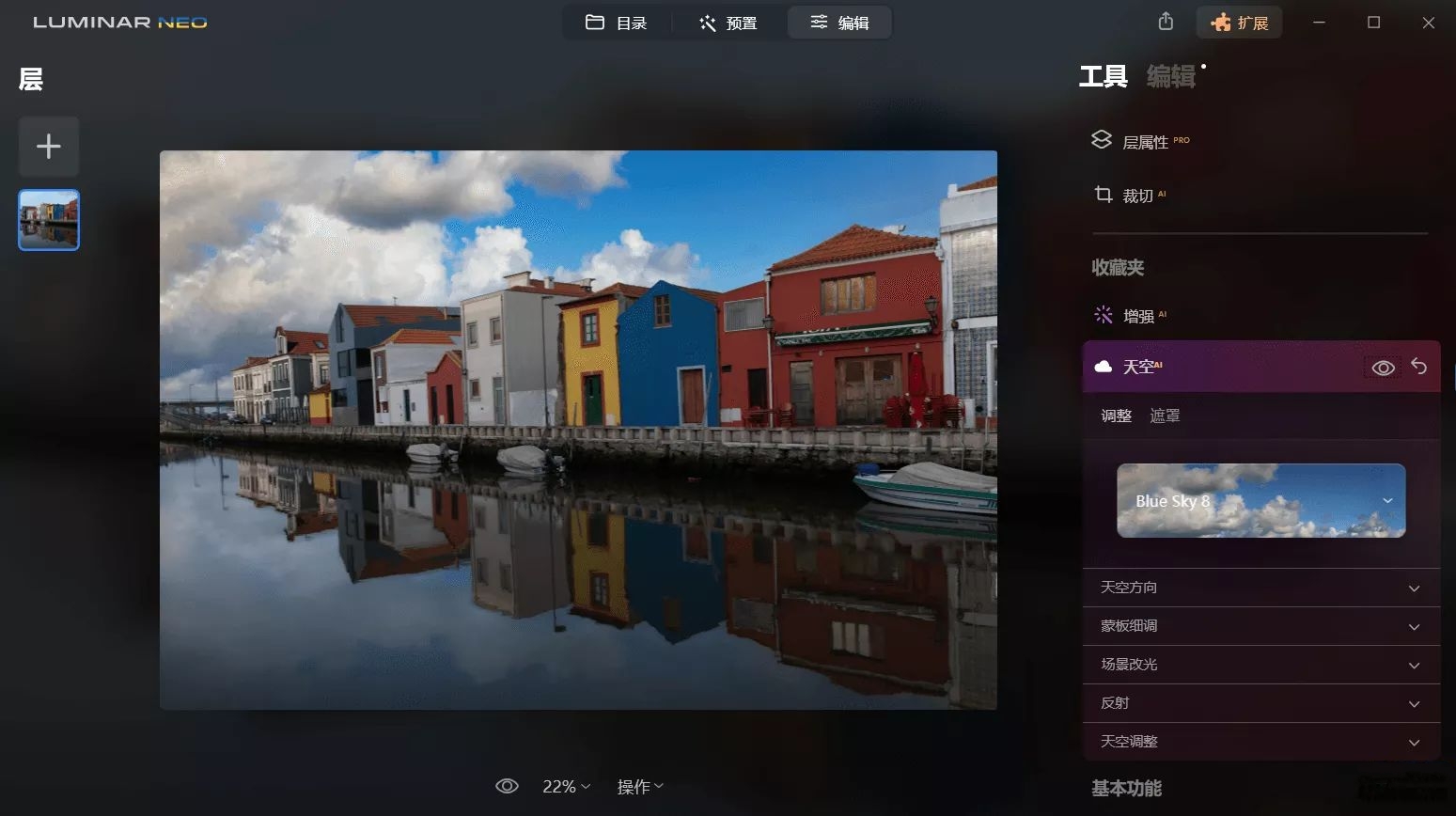
AI图像编辑器 Luminar Neo 便携版 Win1.24.0.14794
如果你对图像编辑有兴趣,但又不想花费太多时间学习复杂的软件操作,那么 Luminar Neo 可能就是你要找的完美工具。作为一款基于AI技术的创意图像编辑器,Luminar Neo简化了复杂的编辑流程,即使是没有任何图像处理经验的新手…...

发币流程是什么,需要多少成本?
这是一个专注于Web3相关开发的账号,具体会讲解步骤以及开发方案 偶尔会有科普,有兴趣的可以点右上角关注一下 发币(发行数字货币)的流程通常涉及技术实现、法律合规、经济模型设计等多个环节,以下是关键步骤的简要说明…...

【fork初体验】
文章目录 Linux 实验:深入理解 fork 系统调用一、实验目的二、实验环境三、实验内容与步骤(一)打印进程的进程 ID 和父进程 ID1. 编写程序2. 编译与运行3. 运行结果 (二)使用 fork 系统调用创建进程并加入循环语句1. 编…...
学习设计模式《六》——抽象工厂方法模式
一、基础概念 抽象工厂模式的本质是【选择产品簇(系列)的实现】; 抽象工厂模式定义:提供一个创建一系列相关或相互依赖对象的接口,而无需指定它们具体的类; 抽象工厂模式功能:抽象工厂的功能是为一系列相关对象或相互依…...

python_BeautifulSoup提取html中的信息
目录 描述: 过程: step one 下载html网页到本地 step two 提取html信息 list_con soup.select(.list-con) [0] li_list list_con.find_all(li) a li.find(span).find(a) title a.get(title) url a.get(href) span li.find(span).find(spa…...

单例设计模式之懒汉式以及线程安全问题
在单例设计模式中,懒汉式(Lazy Initialization) 通过延迟实例化来优化资源使用,但在多线程环境下存在线程安全问题。以下是其核心问题及解决方案的详细解析: 一、基础懒汉式代码(线程不安全) pu…...

今日头条如何查看IP归属地?详细教程与常见问题解答
在当今互联网时代,IP属地信息已成为各大社交平台展示用户真实性的重要标识。今日头条作为国内领先的资讯平台,也提供了IP属地显示功能。那么,今日头条怎么查看IP归属地?本文将详细介绍在今日头条11.9.0版本中如何查看自己和他人的…...

React-Hook
一、基础 Hooks 1、useState - 状态管理 useState 是 React 提供的一个函数,用来在函数组件中声明和修改状态,没有它,函数组件只是一个“静态模板”;有了它,函数组件可以保存和更新数据(比如计数器数值、输…...

前端节流、防抖函数
节流 什么是节流? 节流就是同一个事件 一秒钟他执行了很多次。但是我不想他执行这么多次,我只想让他执行一次 或者两次。 那该怎么办? why baby why 那我想就是他执行的时候 我就设置一个定时器,如果定时器是空的,等会…...

高级java每日一道面试题-2025年4月26日-基础篇[反射篇]-什么是类型擦除?它与反射之间有什么关系?
如果有遗漏,评论区告诉我进行补充 面试官: 什么是类型擦除?它与反射之间有什么关系? 我回答: 类型擦除与反射的深度解析 一、类型擦除(Type Erasure) 类型擦除是Java泛型实现的核心机制,旨在通过编译期处理确保向…...

Centos7系统防火墙使用教程
CentOS 7是一种常见的Linux操作系统,防火墙作为网络安全的第一道防线,对于服务器的安全至关重要。本文将介绍CentOS 7系统中防火墙的使用教程,包括如何开启、关闭、配置以及防火墙规则的添加和删除。 一、查看防火墙状态 在开始操作之前&am…...

缓存与数据库数据一致性:旁路缓存、读写穿透和异步写入模式解析
旁路缓存模式、读写穿透模式和异步缓存写入模式是三种常见的缓存使用模式,以下是对三种经典缓存使用模式在缓存与数据库数据一致性方面更全面的分析: 一、旁路缓存模式(Cache - Aside Pattern) 1.数据读取流程 应用程序首先向缓…...
【物联网】基于LORA组网的远程环境监测系统设计(机智云版)
基于LORA组网的远程环境监测系统设计(机智云版) 演示视频: 简介: 1.本系统有一个主机,两个从机。 2.一主多从的LORA组网通信,主机和两个从机都配备了STM32F103单片机与 LoRa 模块,主机作为中心设备及WIFI网关,负责接收和发送数据到远程物联网平台和手机APP,两个从机…...
