洛谷 P1850 [NOIP 2016 提高组] 换教室
题目传送门
前言
终于自己想出概率期望 d p dp dp 的状态了,但是依旧没能相对转移方程。(招笑)
暴力
这题部分分和特殊情况分给的挺多的,所以先拿部分分。
一、思路
- 先跑一边 F l o y d Floyd Floyd 最短路求出两点间最短距离 d i s i , j dis_{i, j} disi,j。
- 对于 m = 0 m = 0 m=0,答案就是 ∑ i = 1 n − 1 d i s c i , c i + 1 \sum_{i = 1}^{n - 1} dis_{c_{i}, c_{i + 1}} ∑i=1n−1disci,ci+1;
对于所有 n ≤ 20 n \leq 20 n≤20,直接用状态压缩,二进制枚举所有 【申请情况】 与 【同意情况】(注意:这两者不一样,因为申请了不一定同意,所以枚举申请情况之下还要枚举同意情况),直接计算。
二、复杂度
- 空间: O ( v 2 + n ) O(v^2 + n) O(v2+n)。
- 时间:对于 m = 0 m = 0 m=0, O ( v 3 + n ) O(v^3 + n) O(v3+n);对于 n ≤ 20 n \leq 20 n≤20, O ( v 3 + n × 2 n × 2 m ) O(v^3 + n \times 2^n \times 2^m) O(v3+n×2n×2m)。
(当然后者的时间复杂度远远跑不满,因为对于多数数据 m m m 很小,会限制枚举的状态数量)
三、代码
#include <bits/stdc++.h>using namespace std;const int maxn = 2e3 + 7;
const int maxv = 3e2 + 7;
const int inf = 0x3f3f3f3f;int n, m, v, e;
int c[maxn], d[maxn];
double p[maxn];
int dis[maxv][maxv];
void Floyd() {for (int k = 1; k <= v; ++k)for (int i = 1; i <= v; ++i)for (int j = 1; j <= v; ++j)dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
double ans;
int main() {scanf("%d%d%d%d", &n, &m, &v, &e);for (int i = 1; i <= n; ++i) scanf("%d", c + i);for (int i = 1; i <= n; ++i) scanf("%d", d + i);for (int i = 1; i <= n; ++i) scanf("%lf", p + i);memset(dis, inf, sizeof(dis));for (int i = 1; i <= v; ++i) dis[i][i] = dis[0][i] = dis[i][0] = 0;for (int i = 1, a, b, w; i <= e; ++i) {scanf("%d%d%d", &a, &b, &w);dis[a][b] = dis[b][a] = min(w, dis[a][b]);}Floyd();if (m == 0) {for (int i = 1; i < n; ++i)ans += dis[c[i]][c[i + 1]];printf("%.2lf\n", ans);return 0;}ans = 2e9;for (int s = 0; s < (1 << n); ++s) { // 枚举【申请情况】if (__builtin_popcount(s) > m) continue; // 用来计算 s 二进制中有多少个 1 的函数double sum = 0; // 此【申请情况】下的期望for (int ss = s; 1; ss = s & (ss - 1)) { // 枚举【同意情况】double tmp = 0; // 此【同意情况】对【申请情况】的贡献for (int i = 2; i <= n; ++i) {int lst = ((ss & (1 << (i - 1 - 1))) ? d[i - 1] : c[i - 1]);int now = ((ss & (1 << (i - 1))) ? d[i] : c[i]);tmp += dis[lst][now];}for (int i = 1; i <= n; ++i)if (ss & (1 << (i - 1))) tmp *= p[i];else if (s & (1 << (i - 1))) tmp *= 1 - p[i];sum += tmp;if (ss == 0) break;}ans = min(ans, sum);}printf("%.2lf\n", ans);return 0;
}
期望得分 68 p t s 68pts 68pts,实际得分 68 p t s 68pts 68pts。
(洛谷测评机跑出来挺迷的,应该是数据水的问题,前面暴力的数据点一部分没过,后面正解的数据点过了一部分)
正解
概率期望的题一般就是拿 d p dp dp 做。
一、思路
状态设计
- 很明显要有两维的状态 i , j i, j i,j,表示前 i i i 个中选了 j j j 个。
但是由于花费还与上一状态有关(上一个课程是在 c i c_i ci 还是 d i d_i di),所以还要一维表示这个课是否被申请了。 - 设 d p i , j , 0 / 1 dp_{i, j, 0/1} dpi,j,0/1 表示在前 i i i 个课中 申请了(注意不是同意!!) j j j 个,且第 i i i 个课【没被申请 / 被申请了】时的最小期望。
状态转移
- 若当前课程 i i i 不申请,且上一个课程也没有申请,那么转移方程为: d p i , j , 0 = m i n ( d p i , j , d p i − 1 , j , 0 + d i s c i − 1 , c i ) dp_{i, j, 0} = min(dp_{i, j}, dp_{i - 1, j, 0} + dis_{c_{i - 1}, c_i}) dpi,j,0=min(dpi,j,dpi−1,j,0+disci−1,ci)
- 若当前课程 i i i 不申请,但上一个课程申请了,那么转移方程为(转移条件为 j > 0 j > 0 j>0): d p i , j , 0 = m i n ( d p i , j , 0 , d p i − 1 , j , 1 + d i s c i − 1 , c i × ( 1 − k i ) + d i s d i − 1 , c i × k i ) dp_{i, j, 0} = min( dp_{i, j, 0}, dp_{i - 1, j, 1} + dis_{c_{i - 1}, c_{i}} \times (1 - k_i) + dis_{d_{i - 1}, c_i} \times k_{i}) dpi,j,0=min(dpi,j,0,dpi−1,j,1+disci−1,ci×(1−ki)+disdi−1,ci×ki)后面的分别对应【上一次申请没通过】和【上一次申请通过了】;
- 若当前课程 i i i 申请,那么上一次可以申请,也可以不申请,总共有四种情况,在此就不列举出来了(条件当然也是 j > 0 j > 0 j>0)。
边界条件
- 只有一个课程时,申请或不申请期望花费都为 0 0 0,即: d p 1 , 0 , 0 = d p 1 , 1 , 1 = 0 dp_{1,0,0} = dp_{1,1,1} = 0 dp1,0,0=dp1,1,1=0。
- 而对于 d p 1 , 0 , 1 , d p 1 , 1 , 0 dp_{1,0,1},dp_{1,1,0} dp1,0,1,dp1,1,0 这种不合法状态,我们可以先把他们设为正无穷,这样就不会从它门转移了。
答案
- 因为题目说可以不用玩 m m m 次申请,所以答案就是 m i n i = 0 m { d p n , i , 0 , d p n , i , 1 } min_{i = 0}^{m} \left\{dp_{n, i,0}, dp_{n, i, 1} \right\} mini=0m{dpn,i,0,dpn,i,1}。
复杂度
- 空间: O ( v 2 + n × m ) O(v^2 + n \times m) O(v2+n×m);
- 时间: O ( v 3 + n × m ) O(v^3 + n \times m) O(v3+n×m)。
二、代码
#include <bits/stdc++.h>using namespace std;const int maxn = 2e3 + 7;
const int maxv = 3e2 + 7;
const int inf = 0x3f3f3f3f;int n, m, v, e;
int c[maxn], d[maxn];
double p[maxn];
int dis[maxv][maxv];
void Floyd() {for (int k = 1; k <= v; ++k)for (int i = 1; i <= v; ++i)for (int j = 1; j <= v; ++j)dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}double dp[maxn][maxn][2];
double ans;
int main() {scanf("%d%d%d%d", &n, &m, &v, &e);for (int i = 1; i <= n; ++i) scanf("%d", c + i);for (int i = 1; i <= n; ++i) scanf("%d", d + i);for (int i = 1; i <= n; ++i) scanf("%lf", p + i);memset(dis, 63, sizeof(dis));for (int i = 1; i <= v; ++i) dis[i][i] = dis[i][0] = dis[0][i] = 0;for (int i = 1, a, b, w; i <= e; ++i) {scanf("%d%d%d", &a, &b, &w);dis[a][b] = dis[b][a] = min(w, dis[a][b]);}Floyd();for (int i = 0; i <= n; ++i)for (int j = 0; j <= m; ++j)dp[i][j][0] = dp[i][j][1] = 2e9;dp[1][0][0] = dp[1][1][1] = 0;for (int i = 2; i <= n; ++i) {dp[i][0][0] = dp[i - 1][0][0] + dis[c[i - 1]][c[i]];for (int j = 1; j <= min(i, m); ++j) {// 巨丑马蜂dp[i][j][0] = min(dp[i - 1][j][0] + dis[c[i - 1]][c[i]],dp[i - 1][j][1] + dis[c[i - 1]][c[i]] * (1 - p[i - 1]) + dis[d[i - 1]][c[i]] * p[i - 1]);dp[i][j][1] = min(dp[i][j][1], dp[i - 1][j - 1][0] + dis[c[i - 1]][c[i]] * (1 - p[i]) + dis[c[i - 1]][d[i]] * p[i]);dp[i][j][1] = min(dp[i][j][1], dp[i - 1][j - 1][1] + dis[c[i - 1]][c[i]] * (1 - p[i - 1]) * (1 - p[i]) + dis[c[i - 1]][d[i]] * (1 - p[i - 1]) * p[i] + dis[d[i - 1]][c[i]] * p[i - 1] * (1 - p[i]) + dis[d[i - 1]][d[i]] * p[i - 1] * p[i]);}}ans = 2e9;for (int i = 0; i <= m; ++i)ans = min(ans, min(dp[n][i][0], dp[n][i][1]));printf("%.2lf\n", ans);return 0;
}
期望的分 100 p t s 100pts 100pts,实际得分 100 p t s 100pts 100pts。
相关文章:

洛谷 P1850 [NOIP 2016 提高组] 换教室
题目传送门 前言 终于自己想出概率期望 d p dp dp 的状态了,但是依旧没能相对转移方程。(招笑) 暴力 这题部分分和特殊情况分给的挺多的,所以先拿部分分。 一、思路 先跑一边 F l o y d Floyd Floyd 最短路求出两点间最短距…...

C#生成二维码和条形码
C# 实现二维码和条形码生成:从入门到实战 文章目录 C# 实现二维码和条形码生成:从入门到实战一、引言二、准备工作2.1 开发环境搭建2.2 引入相关库 三、生成条形码3.1 条形码基本概念3.2 使用[ZXing.Net](https://ZXing.Net)生成条形码3.2.1 核心代码实现…...

【金仓数据库征文】金仓数据库 KES:MySQL 迁移实用指南
我们都知道,现在企业数字化转型那可是势在必行,数据库迁移这事儿就变得特别关键。金仓数据库的 KingbaseES(简称 KES),就给咱从 MySQL 往 KES 迁移数据库提供了一套超好用的方案。下面咱就讲下 咋用金仓数据库来完成这…...

多态(c++详细版)
一.多态 1.1 多态的概念 多态(polymorphism)的概念:通俗来说,就是多种形态。多态分为编译时多态(静态多态)和运⾏时多态(动态多态),这⾥我们重点讲运⾏时多态,编译时多态(静态多态)和运⾏时多态(动态多态)。编译时多态(静态多态)主…...
内存拆解)
内存泄漏系列专题分析之八:高通相机CamX内存泄漏内存占用分析--通用ION(dmabuf)内存拆解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:内存泄漏系列专题分析之七:高通相机CamX--Android通用ION(dmabuf)内存分配和释放原理 这一篇我们开始讲: 内存泄漏系列专题分析之八:高通相机CamX内存泄漏&内存占用分析--通用ION(dmabuf)内…...

后端项目进度汇报
项目概述 本项目致力于构建一个先进的智能任务自动化平台。其核心技术是一套由大型语言模型(LLM)驱动的后端系统。该系统能够模拟一个多角色协作的团队,通过一系列精心设计或动态生成的处理阶段,来高效完成各种复杂任务ÿ…...

数据结构——二叉树和堆(万字,最详细)
目录 1.树 1.1 树的概念与结构 1.2 树相关的术语 1.3 树的表示法 2.二叉树 2.1 概念与结构 2.2 特殊的二叉树 2.2.1 满二叉树 2.2.2 完全二叉树 2.3 二叉树存储结构 2.3.1 顺序结构 2.3.2 实现顺序结构二叉树 2.3.2.1 堆的概念与结构 2.3.2. 2 堆的插入与删除数据…...

MATLAB基于格拉姆角场与2DCNN-BiGRU的轴承故障诊断模型
本博客来源于CSDN机器鱼,未同意任何人转载。 更多内容,欢迎点击本专栏目录,查看更多内容。 目录 0 引言 1 格拉姆角场原理 2 2DCNN-BiGRU网络结构 3 应用实例 3.1 数据准备 3.2 格拉姆角场数据提取 3.3 网络模型搭建-重中之重 3.4 …...

正点原子IMX6U开发板移植Qt时出现乱码
移植Qt时出现乱码 1、前言2、问题3、总结 1、前言 记录一下正点原子IMX6U开发板移植Qt时出现乱码的解决方法,方便自己日后回顾,也可以给有需要的人提供帮助。 2、问题 用正点原子IMX6U开发板移植Qt时移植Qt后,sd卡里已经存储了Qt的各种库&…...

JVM局部变量表和操作数栈的内存布局
局部变量表和操作数栈 首先看一段Java源码 public class Add_Sample{public int add(int i, int j){int k 100;int result i j k;return result;}public static void main(String[] args){int result new Add_Sample().add(10,20);System.out.println(result);} }使用ja…...

Mockoon 使用教程
文章目录 一、简介二、模拟接口1、Get2、Post 一、简介 1、Mockoon 可以快速模拟API,无需远程部署,无需帐户,免费,跨平台且开源,适合离线环境。 2、支持get、post、put、delete等所有格式。 二、模拟接口 1、Get 左…...

使用 IDEA + Maven 搭建传统 Spring MVC 项目的详细步骤(非Spring Boot)
搭建Spring MVC项目 第一步:创建Maven项目第二步:配置pom.xml第三步:配置web.xml第四步:创建Spring配置文件第五步:创建控制器第六步:创建JSP视图第七步:配置Tomcat并运行目录结构常见问题解决与…...

以下是在 Ubuntu 上的几款PDF 阅读器,涵盖轻量级、功能丰富和特色工具:
默认工具:Evince(GNOME 文档查看器) 特点:Ubuntu 预装,轻量快速,支持基本标注和书签。 安装:已预装,或手动安装: sudo apt install evince功能全面:Okular&…...

3.2.3 掌握RDD转换算子 - 4. 按键归约算子 - reduceByKey()
在本节课中,我们深入学习了Spark RDD的reduceByKey()算子。reduceByKey()主要用于处理元素为(key, value)形式的RDD,能够将相同key的元素聚集并合并,最终返回一个新RDD,其元素类型与原RDD保持一致。通过案例演示,我们首…...
)
AI领域的MCP(Model-Centric Paradigm)
1. 什么是MCP(Model-Centric Paradigm)? MCP(Model-Centric Paradigm)是人工智能开发中的一种核心理念,强调以模型的优化与改进作为主要驱动因素来提升AI系统的表现。在MCP模式下,开发者专注于…...

Pandas比MySQL快?
知乎上有人问,处理百万级数据,Python列表、Pandas、Mysql哪个更快? Pands是Python中非常流行的数据处理库,拥有大量用户,所以拿它和Mysql对比也是情理之中。 实测来看,MySQL > Pandas > Python列表…...

模拟内存管理
文章目录 1. 实验六:内存管理2. 记录内存空间使用情况2.1 全局参数2.2 内存空间相关参数2.3 关键结构体定义2.4 内存系统初始化 3. 记录空闲分区3.1 采用位图的方式记录物理内存中的空闲帧3.1.1 记录方式3.1.2 举例分析 3.2 主要操作3.2.1 初始化空闲帧:…...

大模型调优方法与注意事项
大模型调优(Fine-tuning)是指对预训练的大型语言模型(如GPT、BERT、LLaMA等)进行二次训练,使其适应特定任务或领域的过程。以下是调优的关键步骤、方法和注意事项: 一、调优的核心步骤 任务定义与数据准备 …...

简易的考试系统设计(Web实验)
简易的考试系统设计(Web实验) 1.实验内容与设计思想(一)实验需求(二)设计思路 2.代码展示3.实验小结 1.实验内容与设计思想 (一)实验需求 1.编写两个页面程序,一个HTML…...

【嵌入式开发-SDIO】
嵌入式开发--SDIO ■ SDIO-简介■■■■■ ■ SDIO-简介 SDIO(Secure Digital Input and Output),即安全数字输入输出接口。它是在SD卡接口的基础上发展而来,它可以兼容之前的SD卡,并可以连接SDIO接口设备,比如:蓝牙、…...

基于Kubernetes的Apache Pulsar云原生架构解析与集群部署指南(上)
#作者:闫乾苓 文章目录 概念和架构概述主要特点消息传递核心概念Pulsar 的消息模型Pulsar 的消息存储与分发Pulsar 的高级特性架构BrokerBookKeeperZooKeeper 概念和架构 概述 Pulsar 是一个多租户、高性能的服务器到服务器消息传递解决方案。Pulsar 最初由雅虎开…...

车载网络TOP20核心概念科普
一、基础协议与总线技术 CAN总线 定义:控制器局域网,采用差分信号传输,速率最高1Mbps,适用于实时控制(如动力系统)。形象比喻:如同“神经系统”,负责传递关键控制信号。 LIN总线 定…...

使用JAVA对接Deepseek API实现首次访问和提问
一、标题 参考:https://www.cnblogs.com/saoge/p/18866776 使用JAVA对接Deepseek API实现首次访问和 提问:我有50万能做什么小本生意,举例3个! 二、代码 import java.io.BufferedReader; import java.io.InputStreamReader; import java.…...

【C语言】文件操作(续)
目录 复习: 一⽂件的顺序读写 例子: 前言: 在上篇文章中介绍了文件的类型,文件指针,流,操作的函数。 在本篇文章继续为大家带来文件细节分享,如 顺序读写等等。 复习: fopen是…...

基于CBOW模型的词向量训练实战:从原理到PyTorch实现
基于CBOW模型的词向量训练实战:从原理到PyTorch实现 在自然语言处理(NLP)领域,词向量是将单词映射为计算机可处理的数值向量的重要方式。通过词向量,单词之间的语义关系能够以数学形式表达,为后续的文本分…...
mac连接lniux服务器教学笔记
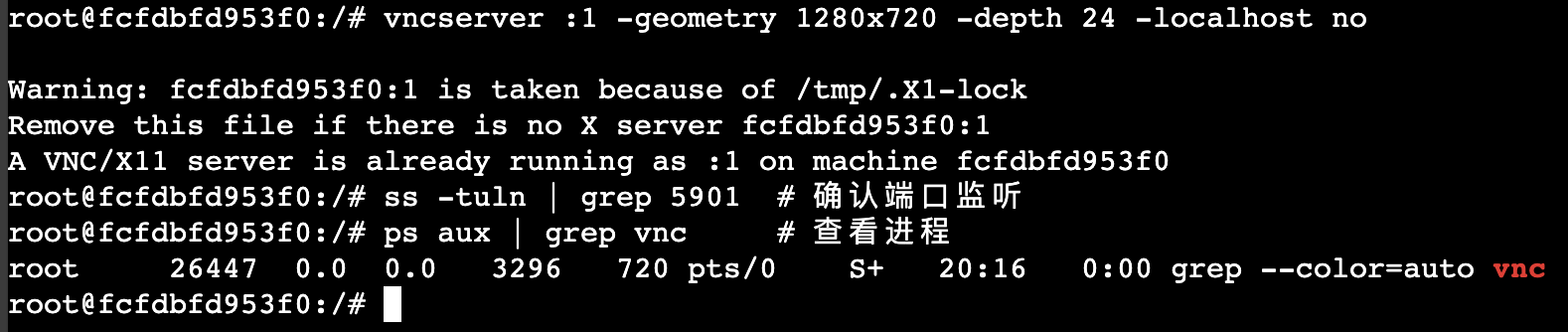
从你的检查结果看,容器内已经安装了 XFCE 桌面环境(xfce.desktop 和 xubuntu.desktop 的存在说明桌面环境已存在)。以下是针对 Docker 容器环境的远程桌面配置方案: 一、容器内快速配置远程桌面(XFCE VNC)…...

vue3 - keepAlive缓存组件
在Vue 3中,<keep-alive>组件用于缓存动态组件或路由组件的状态,避免重复渲染,提升性能。 我们新建两个组件,在每一个组件里面写一个input,在默认情况下当组件切换的时候,数据会被清空,但…...

阀门产业发展方向报告(石油化工阀门应用技术交流大会)
本文大部分内容来自中国通用机械工业协会副会长张宗列在“2024全国石油化工阀门应用技术交流大会”上发表的报告。 一、国外阀门产业发展 从全球阀门市场分布看,亚洲是最大的工业阀门市场,美洲是全球第二大工业阀门市场,欧洲位列第三。 从国…...

Windows Server 2025 安装AMD显卡驱动
运行显卡驱动安装程序,会提示出问题。但是此时资源已经解压 来到驱动路径 C:\AMD\AMD-Software-Installer\Packages\Drivers\Display\WT6A_INF 打开配置文件,把这两行替换掉 %ATI% ATI.Mfg, NTamd64.10.0...16299, NTamd64.10.0, NTamd64.6.0, NTamd64.…...

用 CodyBuddy 帮我写自动化运维脚本
我正在参加CodeBuddy「首席试玩官」内容创作大赛,本文所使用的 CodeBuddy 免费下载链接:腾讯云代码助手 CodeBuddy - AI 时代的智能编程伙伴”。 #CodeBuddy首席试玩官 背景 我个人是非常喜欢 Jenkins 自动化部署工具的,之前都是手写 Jenki…...
