数据结构与算法:图论——最短路径
最短路径
先给出一些leetcode算法题,以后遇见了相关题目再往上增加
最短路径的4个常用算法是Floyd、Bellman-Ford、SPFA、Dijkstra。不同应用场景下,应有选择地使用它们:
- 图的规模小,用Floyd。若边的权值有负数,需要判断负圈。
- 图的规模大,且边的权值非负,用Dijkstra。
- 图的规模大,且边的权值有负数,用SPFA,需要判断负圈。
| 结点N、边M | 边权值 | 选用算法 | 数据结构 |
|---|---|---|---|
| n<200 | 允许有负 | Floyd | 邻接矩阵 |
| n×m<107 | 允许有负 | Bellman-Ford | 邻接表 |
| 更大 | 有负 | SPFA | 邻接表、前向星 |
| 更大 | 无负数 | Dijkstra | 邻接表、前向星 |
2.1、Floyd算法
- Floyed算法:主要是构建 二维矩阵:dp[i][j] 表示从节点 i 到节点 j 最短距离
- 初始化矩阵时:有方向性、并且同一节点的最短距离为0
// floyed 算法vector<vector<int>> dp(n + 1, vector<int>(n + 1, INT_MAX / 2));for (auto a : times) {dp[a[0]][a[1]] = a[2];}for (int i = 0; i <= n; i++) {dp[i][i] = 0;}for (int k = 0; k <= n; k++) for (int i = 0; i <= n; i++) for (int j = 0; j <= n; j++) if (dp[i][j] > dp[i][k] + dp[k][j]) dp[i][j] = dp[i][k] + dp[k][j];1、743. 网络延迟时间
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:

输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1
输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2
输出:-1
提示:
1 <= k <= n <= 1001 <= times.length <= 6000times[i].length == 31 <= ui, vi <= nui != vi0 <= wi <= 100- 所有
(ui, vi)对都 互不相同(即,不含重复边)
// floyed 算法
class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<vector<int>> dp(n + 1, vector<int>(n + 1, INT_MAX / 2));for (auto a : times) {dp[a[0]][a[1]] = a[2];}for (int i = 0; i <= n; i++) {dp[i][i] = 0;}for (int k = 0; k <= n; k++) {for (int i = 0; i <= n; i++) {for (int j = 0; j <= n; j++) {if (dp[i][j] > dp[i][k] + dp[k][j]) {dp[i][j] = dp[i][k] + dp[k][j];}}}}int res = 0;for (int i = 1; i <= n; i++) {if (dp[k][i] == INT_MAX / 2)return -1;res = max(res, dp[k][i]);}return res;}
};
2、1334. 阈值距离内邻居最少的城市
- 这个用floyed直接算即可。无向图构造矩阵时重复操作即可
有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
示例 1:

输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出:3
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是:
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须返回城市 3,因为它的编号最大。
示例 2:

输入:n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出:0
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是:
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 2 以内只有 1 个邻居城市。
class Solution {
public:int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {vector<vector<int>> dp(n, vector<int>(n, INT_MAX / 2));for (auto a : edges) {dp[a[0]][a[1]] = a[2];dp[a[1]][a[0]] = a[2];}for (int k = 0; k < n; k++)for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)if (dp[i][j] > dp[i][k] + dp[k][j])dp[i][j] = dp[i][k] + dp[k][j];// floyed计算完毕,取次数判断即可vector<int> cnt(n, 0);for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (i == j)continue;if (dp[i][j] <= distanceThreshold)cnt[i]++;}}int min = *min_element(cnt.begin(), cnt.end());int res;for (int i = n - 1; i >= 0; i--) {if (min == cnt[i]) {res = i;break;}}return res;}
};
2.2、BellmanFord算法
- Bellman-ford算法的思路也很简单,直接就是两层循环,内层循环所有边,外层循环就是循环所有边的次数。
- 时间复杂度是O(n*m)显然不如dijkstra快
- 优点:它可以处理负权边和负权环的情况。并且可以处理限制次数的问题。
// dp[j] 表示节点k到j的最短路径:并且注意每次更新最短路径,是在上一次的dp上更新:
// a[0] 表示起始节点;a[1] 表示最终节点;a[2]表示a[0]到a[1] 的距离大小。
// a[0]->a[1]距离为a[2]:所以每次更新的都是 dp[a[1]] ,但是需要上一次的整体的predp,来取a[0]节点的最短距离// 最标准的形式有前一个的最小距离的predp
int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<int> dp(n+1,INT_MAX/2);dp[k] = 0;bool flag;while(1){flag = true;vector<int> predp(dp);for(auto a:times){if(dp[a[1]] > predp[a[0]]+a[2]){flag = false;dp[a[1]] = predp[a[0]]+a[2];}}if(flag) break;}int res = *max_element(dp.begin()+1,dp.end());return res==INT_MAX/2?-1:res;}// 然而没有predp也可以,省下来空间
int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<int> dp(n+1,INT_MAX/2);dp[k ] = 0;bool flag;while(1){flag = true;for(auto a:times){if(dp[a[1]] > dp[a[0]]+a[2]){flag = false;dp[a[1]] = dp[a[0]]+a[2];}}if(flag) break;}int res = *max_element(dp.begin()+1,dp.end());return res==INT_MAX/2?-1:res;
}
1、743. 网络延迟时间
示例 1:

输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出:2
// BellmanFord算法 算法复杂度为O(m*n)
class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<int> dp(n+1,INT_MAX/2);dp[k ] = 0;bool flag;while(1){flag = true;// vector<int> predp(dp);for(auto a:times){if(dp[a[1]] > dp[a[0]]+a[2]){flag = false;dp[a[1]] = dp[a[0]]+a[2];}}if(flag) break;}int res = *max_element(dp.begin()+1,dp.end());return res==INT_MAX/2?-1:res;}
};
2、787. K 站中转内最便宜的航班
- 经典使用BellmanFord算法题目:最多经过
k站中转的路线
有 n 个城市通过一些航班连接。给你一个数组 flights ,其中 flights[i] = [fromi, toi, pricei] ,表示该航班都从城市 fromi 开始,以价格 pricei 抵达 toi。
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到出一条最多经过 k 站中转的路线,使得从 src 到 dst 的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出 -1。
示例 1:

输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释:
城市航班图如下
从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200,如图中红色所示。
示例 2:

输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
输出: 500
解释:
城市航班图如下
从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500,图中蓝色所示。
提示:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- 航班没有重复,且不存在自环
0 <= src, dst, k < nsrc != dst
/*BellmanFord算法::外层的路径就是中转的次数,但是注意K++;是中转1此,那么可以使用两条路径使用BellmanFord算法最标准形式:使用predp形式
*/
class Solution {
public:int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {vector<int> dp(n, 1e5+1);dp[src] = 0;k++;while (k--) {vector<int> predp(dp);// 这里最好加&可以大大提高速度for (auto &a : flights) {if(dp[a[1]]>predp[a[0]]+a[2])dp[a[1]] =predp[a[0]]+a[2];}}return dp[dst] == 1e5+1? -1 : dp[dst];}
};
/*不使用BellmanFord算法最标准形式:无predp形式无法准确得到中转次数:结果不对,但是不考虑次数的话,也能得到最短距离
*/// 结果不对
class Solution {
public:int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst,int k) {vector<int> dp(n, 1e5+1);dp[src] = 0;k++;while (k--) {// vector<int> predp(dp);for (auto &a : flights) {if(dp[a[1]]>dp[a[0]]+a[2])dp[a[1]] =dp[a[0]]+a[2];}}return dp[dst] == 1e5+1? -1 : dp[dst];}
};3、1514. 概率最大的路径
- 本题重点是无向图:两边都要操作一次,重复操作即可
- 无向图:说白了就是条件是有向图的两倍,给反转前后节点即可
给你一个由 n 个节点(下标从 0 开始)组成的无向加权图,该图由一个描述边的列表组成,其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边,且该边遍历成功的概率为 succProb[i] 。
指定两个节点分别作为起点 start 和终点 end ,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。
如果不存在从 start 到 end 的路径,请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ,就会被视作正确答案。
示例 1:

输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出:0.25000
解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,而另一条为 0.5 * 0.5 = 0.25
示例 2:

输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出:0.30000
示例 3:

输入:n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出:0.00000
解释:节点 0 和 节点 2 之间不存在路径
提示:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1- 每两个节点之间最多有一条边
class Solution {
public:double maxProbability(int n, vector<vector<int>>& edges,vector<double>& succProb, int start_node,int end_node) {vector<double> dp(n, 0);dp[start_node] = 1;while (1) {bool flag = true;for (int i = 0; i < succProb.size(); i++) {// 双向图:反转前后再操作一次即可if (dp[edges[i][1]] < dp[edges[i][0]] * succProb[i]) {flag = false;dp[edges[i][1]] = dp[edges[i][0]] * succProb[i];}if (dp[edges[i][0]] < dp[edges[i][1]] * succProb[i]) {flag = false;dp[edges[i][0]] = dp[edges[i][1]] * succProb[i];}}if (flag) break;}return dp[end_node];}
};
3、1334. 阈值距离内邻居最少的城市
- 这个用floyed直接算即可。使用bellmanFord可以做
有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
示例 1:

输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出:3
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是:
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须返回城市 3,因为它的编号最大。
示例 2:

输入:n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出:0
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是:
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 2 以内只有 1 个邻居城市。
class Solution {
public:int targetnum(int n, vector<vector<int>>& edges, int distanceThreshold,int k) {vector<int> dp(n, INT_MAX / 2);dp[k] = 0;while (1) {bool flag = true;vector<int> predp(dp);for (auto& a : edges) {if (dp[a[1]] > predp[a[0]] + a[2]) {flag = false;dp[a[1]] = predp[a[0]] + a[2];}if (dp[a[0]] > predp[a[1]] + a[2]) {flag = false;dp[a[0]] = predp[a[1]] + a[2];}}if (flag)break;}int res = 0;/*这里注意:这个是排除本身for (int i = 0; i < n; i++) {if (i == k)continue;if (dp[i] <= distanceThreshold) {res++;}}若改成:只要碰到i!=k,则跳出这个for循环,后面都不执行了for (int i = 0; i < n && i!=k; i++) {if (dp[i] <= distanceThreshold) {res++;}}*/for (int i = 0; i < n; i++) {if (i == k)continue;if (dp[i] <= distanceThreshold) {res++;}}return res;}// 找到最右边的最小值及坐标。int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {int min_num = 200;int res = 0;for(int i = 0;i<n;i++){int mid = BellmabFord( n, edges, i, distanceThreshold);if(mid<=min_num){min_num = mid;res = i; }}return res;}// 直观但臃肿。int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {int minn = INT_MAX / 2;vector<int> res;for (int i = 0; i < n; i++) {res.push_back(targetnum(n, edges, distanceThreshold, i));}int sul = 0;int minnub = *min_element(res.begin(), res.end());for (int i = n - 1; i >= 0; i--) {if (res[i] == minnub) {sul = i;break;}}return sul;}
};
2.3、dijkstra算法
- 基础型:图的规模大,且边的权值非负,用Dijkstra。时间复杂度O(N*N)。可以看出时间复杂度 只和 n (节点数量)有关系。
// dijkstra算法基础版/*基础版:适用于题目中给出距离矩阵,给出矩阵
*/
vector<int> dijkstra(vector<vector<int>>& value, int start) {//需要一个二维矩阵从0到n,0基本上没有用,无关的都是INT_MAX / 2//对角线为0//返回了一个value[i][j]表示从i到j的最短路径,但是i,j不为0int len = value.size(); // len = n + 1;int n = len - 1;vector<int> res(len, INT_MAX);res[start] = 0;vector<bool> visit(len, false);for (int i = 1; i <= n; i++) {// 找到最小蓝的位置int minbule = 0;for (int j = 1; j <= n; j++) {if (!visit[j] && res[minbule] > res[j]) {minbule = j;}}if(visited[blue]) continue;// 把最小蓝变成白色visit[minbule] = true;// 更新所有最短距离for (int j = 1; j <= n; j++) {res[j] = min(res[j], res[minbule] + value[minbule][j]);}}return res;
}
- 堆优化型:使用边数,边数少的,堆优化比较好。时间复杂度:O(E * (N + logE)) E为边的数量,N为节点数量。
- 适用条件:但 n 很大,边 的数量 很小的时候(稀疏图),是不是可以换成从边的角度来求最短路呢?
int dijkstra_networkDelayTime2(vector<vector<int>>& times, int n, int k) {unordered_map<int, vector<pair<int, int > > > mp;for (auto a : times) {mp[a[0]].push_back({a[1], a[2]});}// 不一定要用map,使用vector效果一样:只不过是保存a[0]点指向的节点和距离vector<vector<pair<int, int>>> g(n);for (auto &t : times) {int x = t[0] - 1, y = t[1] - 1;g[x].emplace_back(y, t[2]);}作者:力扣官方题解
链接:https://leetcode.cn/problems/network-delay-time/solutions/909575/wang-luo-yan-chi-shi-jian-by-leetcode-so-6phc/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。vector<int> dismin(n + 1, INT_MAX / 2);vector<bool> visited(n + 1, false);dismin[k] = 0;// 优先队列<蓝点的最短距离,蓝点坐标>小顶堆priority_queue< pair<int, int>, vector<pair<int, int> >, greater<> > que;que.push({0, k});while (!que.empty()) {int minblue = que.top().second;que.pop();// 变成白点if (visited[minblue]) continue;visited[minblue] = true;// 增加这个白点会有什么影响对于 dismin// 遍历所有与新白点连接的蓝点for (pair<int, int > a : mp[minblue]) {if (!visited[a.first] && dismin[a.first] > a.second + dismin[minblue] ) {dismin[a.first] = a.second + dismin[minblue];que.push({dismin[a.first], a.first});}}}int res = *max_element(dismin.begin() + 1, dismin.end());return res == INT_MAX / 2 ? -1 : res;
}
-
时间复杂度:O(E * (N + logE)) E为边的数量,N为节点数量
-
空间复杂度:O(log(N^2))
-
while (!pq.empty()) 时间复杂度为 E ,while 里面 每次取元素 时间复杂度 为 logE,和 一个for循环 时间复杂度 为 N 。所以整体是 E * (N + logE)
-
sort排序与大顶堆
- 优先队列
- less<>表示从上到下是递减的
- greater<>表示从上到下是递增的
#include <bits/stdc.h> using namespace std;// priority_queue // less<>表示从上到下是递减的 // greater<>表示从上到下是递增的 // 默认 不加默认less<> 大顶堆就是less<> // 如果想要头上最小需要加上greater<> void prio_int() {vector<int> strs = {5,8,2,6,1,8,2};priority_queue<int, vector<int>, less<>> que(strs.begin(),strs.end());while(que.empty()==0){cout<<que.top()<<endl;que.pop();}return; }// 优先队列的自定义 // 优先队列与传统sort的相反 void prio_string() {vector<string> strs = {"xhh", "mmcy", "mi", "xhz", "abcdef"};struct cmp{bool operator()(string a,string b){return a.size()<b.size()||(a.size()==b.size() && a>b);}};priority_queue<string, vector<string>, cmp> que(strs.begin(),strs.end());while(que.empty()==0){cout<<que.top()<<endl;que.pop();}return; }// map自动排序,unordered_map 不排序,想排序直接用 // vector<pair<int,string>>来重新装一下,再排序 void sort_map_int() {map<int, string> mp = {{1, "ab"}, {8, "zx"}, {5, "ac"}, {4, "ae"}};for (auto a : mp) {cout << a.first << "->" << a.second << endl;}return ; }// sort pair使用 a.first a.second // 类型使用auto肯定是对的,但是可能没有提示first、second void sort_pair_int() {vector<pair<int, string>> test_vector = {{5, "abc"}, {1, "ac"}, {1, "ad"}, {2, "ac"}};sort(test_vector.begin(), test_vector.end(), [](auto a, auto b) {return (a.first > b.first || (a.first == b.first && a.second > b.second));});for (auto a : test_vector ) {cout << a.first << "->" << a.second << endl;}return ; }void sort_vector_int() {vector<int> test_vector = {5, 4, 9, 7};sort(test_vector.begin(), test_vector.end(), [](auto a, auto b) {return a > b;});for (auto a : test_vector ) {cout << a << " ";}cout << endl;return ; }void sort_vector_vector_int() {vector<vector<int>> test_vector = {{1, 2}, {9, 8}, {1, 3}, {8, 2}, {6, 5}};sort(test_vector.begin(), test_vector.end(), [](auto a, auto b) {return (a[0] < b[0] || (a[0] == b[0] && a[1] < b[1]));});for (auto a : test_vector ) {for (auto b : a) {cout << b << " ";}cout << endl;}return ; }int main() {sort_vector_int();cout << "****************" << endl;sort_vector_vector_int();cout << "****************" << endl;sort_pair_int();cout << "****************" << endl;sort_map_int();cout << "****************" << endl;prio_string();cout << "****************" << endl;prio_int(); }
1、743. 网络延迟时间
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:

输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1
输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2
输出:-1
提示:
1 <= k <= n <= 1001 <= times.length <= 6000times[i].length == 31 <= ui, vi <= nui != vi0 <= wi <= 100- 所有
(ui, vi)对都 互不相同(即,不含重复边)
/*普通版本
*/class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<int> dp(n + 1, INT_MAX / 2);dp[k] = 0;vector<vector<int>> dis(n + 1, vector<int>(n + 1, INT_MAX / 2));for (auto& a : times) {dis[a[0]][a[1]] = a[2];}vector<int> visited(n + 1, false);//for(int i = 0;i<=n;i++){while(1) {int blue = 0;for (int i = 0; i <= n; i++) {if (!visited[i] && dp[blue] > dp[i]) {blue = i;}}// 再次遇到说明最小值就是0了,结束了if(visited[blue]) break;visited[blue] = true;for (int i = 0; i <= n; i++) {if (dp[i] > dp[blue] + dis[blue][i]) {dp[i] = dp[blue] + dis[blue][i];}}}int res = *max_element(dp.begin() + 1, dp.end());return res == INT_MAX / 2 ? -1 : res;}
};// 堆优化版本
class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> que;// que.push({k,0});que.push({0, k});vector<bool> visited(n + 1, false);vector<int> dp(n + 1, INT_MAX / 2);dp[k] = 0;while (!que.empty()) {auto blue = que.top();que.pop();// 这里不用想那么多:看见置true直接在前面加判断if( visited[blue.second]) continue;visited[blue.second] = true;for (auto& a : times) {// 这里直接取头节点不是这个blue的直接跳过,已经为白的直接跳过// 目的是为了取最小的蓝if (a[0] != blue.second || visited[a[1]] )continue;if (dp[a[1]] > dp[blue.second] + a[2]) {dp[a[1]] = dp[blue.second] + a[2];que.push({dp[a[1]], a[1]});}}}int res = *max_element(dp.begin() + 1, dp.end());return res == INT_MAX / 2 ? -1 : res;}
};
2、1334. 阈值距离内邻居最少的城市
- 直接使用堆优化:注意双向图即可
有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
示例 1:

输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出:3
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是:
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须返回城市 3,因为它的编号最大。
示例 2:

输入:n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出:0
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是:
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 2 以内只有 1 个邻居城市。
/*无向图的堆优化djikstra算法:
*/
class Solution {
public:int target(int n, vector<vector<int>>& edges, int distanceThreshold,int k) {priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> que;que.push({0, k});vector<int> dis(n, INT_MAX / 2);dis[k] = 0;vector<bool> visited(n, false);while (!que.empty()) {int blue = que.top().second;que.pop();if (visited[blue])continue;visited[blue] = true;for (auto& a : edges) {if (a[0]==blue && dis[a[1]] > dis[a[0]] + a[2]) {dis[a[1]] = dis[a[0]] + a[2];que.push({dis[a[1]], a[1]});}if (a[1]==blue && dis[a[0]] > dis[a[1]] + a[2]) {dis[a[0]] = dis[a[1]] + a[2];que.push({dis[a[0]], a[0]});}}}int res = 0;for (auto& a : dis) {if (a <= distanceThreshold)res++;}return res;}int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {int res = INT_MAX / 2;int resdex = 0;for (int i = 0; i < n; i++) {int mid = target(n, edges, distanceThreshold, i);if (mid <= res) {res = mid;resdex = i;}}return resdex;}
};
相关文章:

数据结构与算法:图论——最短路径
最短路径 先给出一些leetcode算法题,以后遇见了相关题目再往上增加 最短路径的4个常用算法是Floyd、Bellman-Ford、SPFA、Dijkstra。不同应用场景下,应有选择地使用它们: 图的规模小,用Floyd。若边的权值有负数,需要…...

提示词工程:通向AGI时代的人机交互艺术
引言:从基础到精通的提示词学习之旅 欢迎来到 "AGI时代核心技能" 系列课程的第二模块——提示词工程。在这个模块中,我们将系统性地探索如何通过精心设计的提示词,释放大型语言模型的全部潜力,实现高效、精…...

FreeRTOS系统CPU使用率统计
操作系统中CPU使用率是在软件架构设计中必须要考虑的一个重要性能指标。它直接影响到程序的执行时间以及优先级更高的任务能否实时响应的问题。而CPU使用率也不能过低,避免资源浪费。 基本原理 操作系统会统计系统总共运行了多少时间,以及在此期间每个任…...

是更换Window资源管理器的时候了-> Files-community/Files
Files • 主页https://files.community/ 它已经做到了 云盘文件集成、标签页和多种布局、丰富的文件预览…… 您想要的一切现代文件管理器的强大功能, Files 都能做到。 概述 Files 是一个现代文件管理器,可帮助用户组织他们的文件和文件夹。Files 的…...

基于windows安装MySQL8.0.40
基于windows安装MySQL8.0.40 基于windows 安装 MySQL8.0.40,解压文件到D:\mysql-8.0.40-winx64 在D:\mysql-8.0.40-winx64目录下创建my.ini文件,并更新一下内容 [client] #客户端设置,即客户端默认的连接参数 # 设置mysql客户端连接服务…...

【Vue】组件自定义事件 TodoList 自定义事件数据传输
目录 一、绑定 二、解绑 组件自定义事件总结 TodoList案例对数据传输事件的修改 总结不易~ 本章节对我有很大收获, 希望对你也是!!! 本章节素材已上传Gitee:yihaohhh/我爱Vue - Gitee.com 前面我们学习的clikc、…...

基于Centos7的DHCP服务器搭建
一、准备实验环境: 克隆两台虚拟机 一台作服务器:DHCP Server 一台作客户端:DHCP Clinet 二、部署服务器 在网络模式为NAT下使用yum下载DHCP 需要管理员用户权限才能下载,下载好后关闭客户端,改NAT模式为仅主机模式…...

LabVIEW超声波液位计检定
在工业生产、运输和存储等环节,液位计的应用十分广泛,其中超声波液位计作为非接触式液位测量设备备受青睐。然而,传统立式水槽式液位计检定装置存在受建筑高度影响、量程范围受限、流程耗时长等问题,无法满足大量程超声波液位计的…...

Ubuntu 24.04 完整Docker安装指南:从零配置到实战命令大全
文章目录 1. 安装 Docker2. 配置 Docker 镜像加速器2.1 配置 Docker 镜像源2.2 重启 Docker 服务 3. Docker 常用命令3.1 Docker 常用命令速查表3.1.1 容器管理3.1.2 镜像管理3.1.3 网络管理3.1.4 数据卷管理3.1.5 容器资源管理3.1.6 Docker Compose(容器编排&#…...

[STM32] 4-2 USART与串口通信(2)
文章目录 前言4-2 USART与串口通信(2)数据发送过程双缓冲与连续发送数据发送过程中的问题 数据接收过程TXE标志位(发送数据寄存器空)TC标志位(发送完成标志位)单个数据的发送数据的连续发送 接收过程中遇到的问题问题描述…...

基于Python+MongoDB猫眼电影 Top100 数据爬取与存储
前言:从猫眼电影排行榜页面(TOP100榜 - 猫眼电影 - 一网打尽好电影 )爬取 Top100 电影的电影名称、图片地址、主演、上映时间和评分等关键信息,并将这些信息存储到本地 MongoDB 数据库中,🔗 相关链接Xpath&…...

前端缓存踩坑指南:如何优雅地解决浏览器缓存问题?
浏览器缓存,配置得当,它能让页面飞起来;配置错了,一次小小的上线,就能把你扔进线上 bug 的坑里。你可能遇到过这些情况: 部署上线了,结果用户还在加载旧的 JS;接口数据改了…...

Ubuntu 单机多卡部署脚本: vLLM + DeepSeek 70B
# 部署脚本:Ubuntu vLLM DeepSeek 70B # 执行前请确保:1. 系统为 Ubuntu 20.04/22.04 2. 拥有NVIDIA显卡(显存≥24G) # 保存两个文件 1 init.sh 初始化 2、test.sh 测试 # init.sh #!/bin/bash # 系统更新与基础依赖sudo apt update && s…...

从软件到硬件:三大主流架构的特点与优劣详解
常见的架构包括软件架构、企业架构、硬件架构等,以下是对这几种常见架构的分析: 一、软件架构 1.分层架构 描述:分层架构是一种经典的软件架构模式,将软件系统按照功能划分为不同的层次,一般包括表现层(…...

STM32printf重定向到串口含armcc和gcc两种方案
STM32串口重定向:MDK与GCC环境下需重写的函数差异 在嵌入式开发中,尤其是使用 STM32系列微控制器 的项目中,调试信息的输出是不可或缺的一部分。为了方便调试,开发者通常会选择将 printf 等标准输出函数通过 UART 串口发送到 PC …...

为了摸鱼和吃瓜,我开发了一个网站
平时上班真的比较累,摸鱼和吃瓜还要跳转多个平台的话,就累上加累了。 所以做了一个聚合了全网主流平台热搜的网站。 目前市面上确实有很多这种网站了,所以目前最主要有两点和他们不同: 给热搜列表增加了配图,刷的时候…...

Webug4.0靶场通关笔记11- 第15关任意文件下载与第16关MySQL配置文件下载
目录 一、文件下载 二、第15关 任意文件下载 1.打开靶场 2.源码分析 3.渗透实战 三、第16关 MySQL配置文件下载 1.打开靶场 2.源码分析 3.渗透实战 (1)Windows系统 (2)Linux系统 四、渗透防御 一、文件下载 本文通过…...

【中间件】brpc_基础_remote_task_queue
文章目录 remote task queue1 简介2 核心功能2.1 任务提交与分发2.2 无锁或低锁设计2.3 与 bthread 深度集成2.4 流量控制与背压 3 关键实现机制3.1 数据结构3.2 任务提交接口3.3 任务窃取(Work Stealing)3.4 同步与唤醒 4 性能优化5 典型应用场景6 代码…...

maven坐标导入jar包时剔除不需要的内容
maven坐标导入jar包时剔除不需要的内容 问题描述解决方案 问题描述 maven坐标导入jar包时剔除不需要的内容 解决方案 Spring Boot 默认使用 Logback,需在 pom.xml 中排除其依赖: <dependency><groupId>org.springframework.boot</gro…...
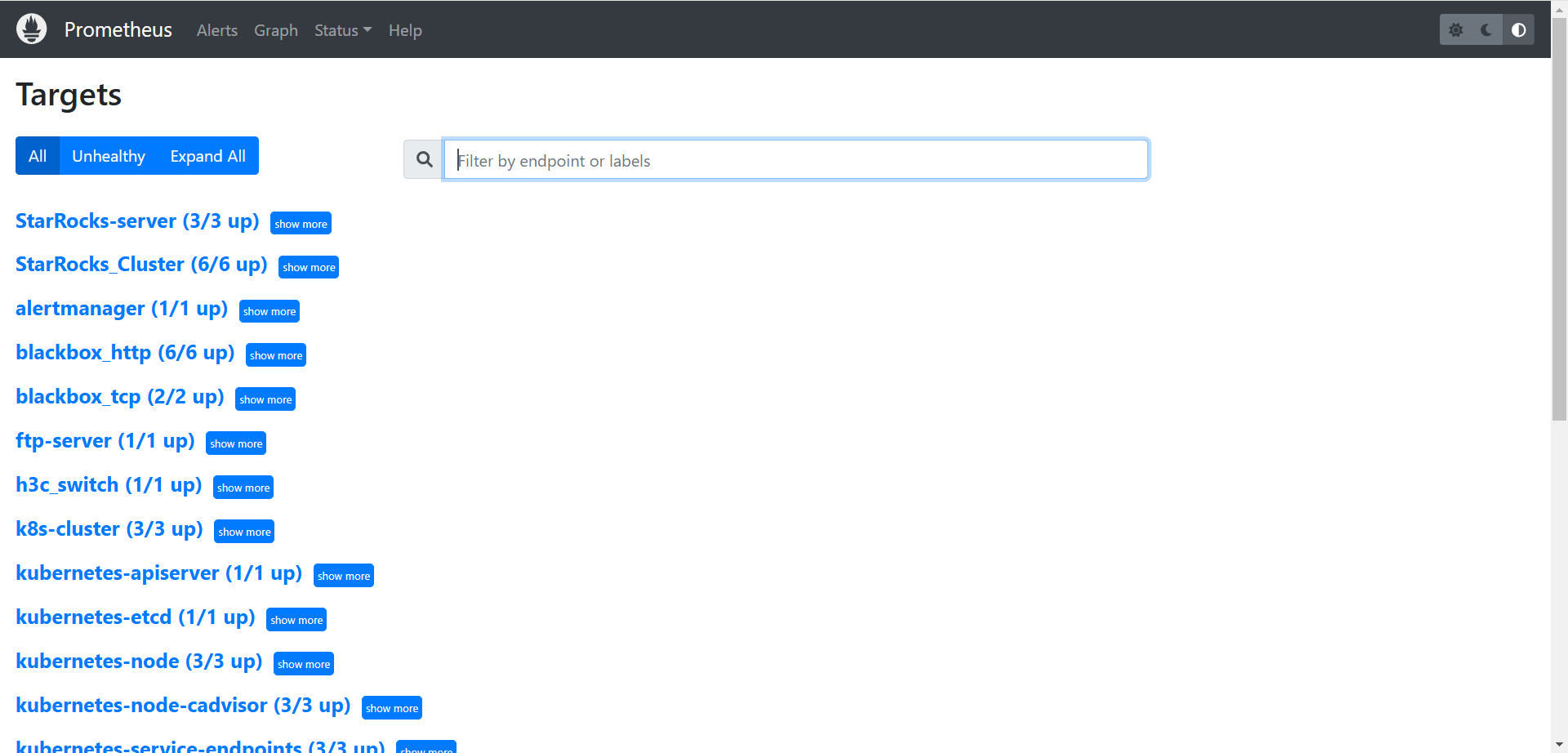
k8s监控方案实践(一):部署Prometheus与Node Exporter
k8s监控方案实践(一):部署Prometheus与Node Exporter 文章目录 k8s监控方案实践(一):部署Prometheus与Node Exporter一、Prometheus简介二、PrometheusNode Exporter实战部署1. 创建Namespace(p…...

ValueError: Could not find common ancestor of[]
ValueError: Could not find common ancestor of [0004_deadstockstathistorymodel, 0026_remove_orderdetailmodel_order_no]说明 Django 当前在 尝试生成迁移或者执行迁移 时,发现你的迁移历史“断裂”了: 你这个 App 的迁移历史有两个分支,…...

具身系列——比较3种vpg算法方式玩CartPole游戏(强化学习)
文档1方式参考:https://gitee.com/chencib/ailib/blob/master/rl/vpg_baseline_cartpole.py 文档2方式参考:https://gitee.com/chencib/ailib/blob/master/rl/vpg_batchupdate_cartpole.py 文档3方式参考:https://gitee.com/chencib/ailib/bl…...

面向未来的 TCP 协议设计:可扩展与兼容并存
目录 1.设计思路 (1)完整数据结构(字节布局) 1)字段解释: 2)Flags字段设计(1字节位图) (2)进阶版 Java 解码器实现(示例…...

PyTorch_自动微分模块
自动微分 (Autograd) 模块对张量做了进一步的封装,具有自动求导功能。自动微分模块是构成神经网络训练的必要模块,在神经网络的反向传播过程中,Autograd 模块基于正向计算的结果对当前的参数进行微分计算,从而实现网络权重参数的更…...

【Git】【commit】查看未推送的提交查看指定commit的修改内容合并不连续的commit
文章目录 1. 查看未推送的提交方法一 :git status方法二:git log方法三:git cherry方法四:git rev-list 2. 查看指定commit的修改方法一:git show方法二:git log方法三:git diff 3. 合并不连续的…...

手写 Vue 源码 === 依赖清理机制详解
目录 引言 响应式系统基础回顾 依赖清理的必要性 ReactiveEffect 类的设计 依赖清理的三个关键函数 1. preCleanEffect:执行前的准备 2. trackEffects:依赖收集与 diff 算法 3. postCleanEffect:执行后的清理 4. cleanDepEffect:清理依赖 实际案例分析 依赖清理算…...

LSB图像信息隐藏系统(MATLAB)
图像信息隐藏系统 系统概述 图像信息隐藏系统是一个基于MATLAB开发的图像隐写工具,采用自适应LSB(最低有效位)隐写算法,实现了信息在图像中的隐藏与提取功能。系统配备了直观的图形用户界面,支持图像分析、信息隐藏、…...

C++GO语言微服务项目之 go语言基础语法
目录 01 变量定义 02 自增语法 03 指针 04 go不支持的语法 05 string 06 定长数组-forrange 07 动态数组追加元素 08 切片截取-copy-make介绍 09 map介绍 10 函数 11 内存逃逸 12 import 13 命令行参数-switch 14 标签与continue-goto-break配合使用 15 枚举cons…...

DDR在PCB布局布线时的注意事项及设计要点
一、布局注意事项 控制器与DDR颗粒的布局 靠近原则:控制器与DDR颗粒应尽量靠近,缩短时钟(CLK)、地址/控制线(CA)、数据线(DQ/DQS)的走线长度,减少信号延迟差异。 分组隔…...

【每天学习一点点】使用Python的pathlib模块分割文件路径
使用Python的pathlib模块分割文件路径 pathlib模块(Python 3.4)提供了面向对象的文件系统路径操作方式,比传统的os.path更加直观和易用。以下是使用pathlib分割文件路径的几种方法: 基本路径分割 from pathlib import Path# 创…...
