两种方法求解最长公共子序列问题并输出所有解
最长公共子序列(Longest Common Subsequence, LCS)是动态规划领域的经典问题,广泛应用于生物信息学(如DNA序列比对)、文本差异比对(如Git版本控制)等领域。本文将通过自顶向下递归+记忆化、自底向上动态规划以及回溯法找所有解三种方法,深入剖析LCS问题的求解过程,并提供完整的代码实现与实例验证
1.1 什么是LCS?
给定两个字符串text1和text2,其最长公共子序列定义为:在不改变字符相对顺序的前提下,两个字符串共有的最长字符序列。例如,text1=“abcde”,text2=“ace"的LCS为"ace”,长度为3。
1.2 动态规划的核心思想
动态规划通过分解问题、存储中间状态(即子问题的解)来避免重复计算。对于LCS问题,定义状态dp[i][j]表示text1前i个字符与text2前j个字符的LCS长度。状态转移方程如下:

边界条件为dp[0][j]=0和dp[i][0]=0,即空字符串的LCS长度为0。
算法实现与优化
2.1 自顶向下递归+记忆化(Top-Down)
通过递归分解问题,并用二维数组memo存储已计算的子问题结果,避免重复计算。
int upToDown(string& a, string& b, int m, int n, vector<vector<int>>& memo) {if (m == 0 || n == 0) return 0;if (memo[m][n] != -1) return memo[m][n]; // 记忆化查询if (a[m-1] == b[n-1]) {memo[m][n] = 1 + upToDown(a, b, m-1, n-1, memo);} else {memo[m][n] = max(upToDown(a, b, m-1, n, memo), upToDown(a, b, m, n-1, memo));}return memo[m][n];
}
时间复杂度:O(mn),空间复杂度:O(mn)。
2.2 自底向上动态规划(Bottom-Up)
通过迭代填充二维数组dp,从最小子问题逐步求解最终结果。
void downToUp(string a, string b) {int m = a.length(), n = b.length();vector<vector<int>> dp(m+1, vector<int>(n+1, 0));for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (a[i-1] == b[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;} else {dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}}}cout << "LCS长度:" << dp[m][n];
}
优势:无需递归栈,适合大规模输入。
回溯法找所有最优解
3.1 回溯原理
基于动态规划表dp,从dp[m][n]反向追踪所有可能的路径。当字符相等时向左上回溯,否则根据dp值选择向上或向左回溯。
void LCS_Backtrack(string& X, string& Y, vector<vector<int>>& dp, int i, int j, string current, vector<string>& result) {if (i == 0 || j == 0) {reverse(current.begin(), current.end());result.push_back(current);return;}if (X[i-1] == Y[j-1]) {current.push_back(X[i-1]);LCS_Backtrack(X, Y, dp, i-1, j-1, current, result);current.pop_back();} else {if (dp[i-1][j] == dp[i][j]) {LCS_Backtrack(X, Y, dp, i-1, j, current, result);}if (dp[i][j-1] == dp[i][j]) {LCS_Backtrack(X, Y, dp, i, j-1, current, result);}}
}
注意:由于回溯路径是从后向前构建,最终需要反转字符串。
测试案例 && 完整代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100;// 自底向上
void downToUp(string a, string b) {int al = a.length();int bl = b.length();int D[N][N];for (int i = 1; i <= al; i++) {for (int j = 1; j <= bl; j++) {if (a[i - 1] == b[j - 1]) {D[i][j] = D[i - 1][j - 1] + 1;} else {D[i][j] = max(D[i - 1][j], D[i][j - 1]);}}}cout << "最长公共子序列长度: " << D[al][bl] << endl;
}// 自上向下,传入的二维数组初始化为一
int upToDown(string& a, string& b, int m, int n, vector<vector<int>>& memo) {if (m == 0 || n == 0) return 0; // 递归终止条件if (memo[m][n] != -1) return memo[m][n]; // 计算过直接返回结果if (a[m - 1] == b[n - 1]) {memo[m][n] = 1 + upToDown(a, b, m - 1, n - 1, memo);} else {memo[m][n] = max(upToDown(a, b, m - 1, n, memo), upToDown(a, b, m, n - 1, memo));}return memo[m][n];
}// 3. 回溯法找到所有最长公共子序列
void LCS_Backtrack(string& X, string& Y, vector<vector<int>>& dp, int m, int n, string& current, vector<string>& result) {// 如果到达矩阵的边界,表示一个公共子序列的结束if (m == 0 || n == 0) {result.push_back(current); // 到达边界,记录一个解return;}// 如果当前字符相等,将字符加入当前子序列,回溯到左上角if (X[m - 1] == Y[n - 1]) {current.push_back(X[m - 1]); // 字符匹配,添加到当前子序列LCS_Backtrack(X, Y, dp, m - 1, n - 1, current, result);current.pop_back(); // 回溯,移除字符} else {// 如果上方 dp 值等于当前 dp 值,说明从上面来的if (dp[m - 1][n] == dp[m][n]) {LCS_Backtrack(X, Y, dp, m - 1, n, current, result); // 向上回溯}// 如果左边 dp 值等于当前 dp 值,说明从左边来的if (dp[m][n - 1] == dp[m][n]) {LCS_Backtrack(X, Y, dp, m, n - 1, current, result); // 向左回溯}}
}int main() {string a, b;cin >> a >> b;int m = a.length();int n = b.length();vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (a[i - 1] == b[j - 1]) {dp[i][j] = 1 + dp[i - 1][j - 1]; } else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); }}}vector<string> result;string current;LCS_Backtrack(a, b, dp, m, n, current, result);cout << "所有的最长公共子序列: " << endl;for (const auto& seq : result) {string re = seq;reverse(re.begin(), re.end());cout << re << endl;}return 0;
}输入
ABCBDAB
BDCABC
输出
4
所有的最长公共子序列:
BCAB
BDAB
end
相关文章:

两种方法求解最长公共子序列问题并输出所有解
最长公共子序列(Longest Common Subsequence, LCS)是动态规划领域的经典问题,广泛应用于生物信息学(如DNA序列比对)、文本差异比对(如Git版本控制)等领域。本文将通过自顶向下递归记忆化…...

【Linux网络】网络协议基础
网络基础 计算机网络背景 独立模式:计算机之间相互独立 网络互联:多台计算机连接在一起,完成数据共享 局域网LAN:计算机数量更多了,通过交换机和路由器连接在一起 广域网WAN:将远隔千里的计算机都连在一起 所谓"局域网"和"广域网"只是一个相对的概念.比…...

挑战用豆包教我学Java01天
今天是豆包教我学Java的第一天,废话不多说直接开始。 1.每日题目: 基础语法与数据类型 题目:编写一个 Java 程序,从控制台读取两个整数,然后计算它们的和、差、积、商,并输出结果。题目:编写…...

0903Redux改造项目_用户信息_状态管理-react-仿低代码平台项目
文章目录 1 Redux管理用户信息1.1 定义store和reducer1.2 使用useSeletor 2 自定义Hook统一加载用户信息存储Redux3 根据用户登录状态动态跳转页面结语 1 Redux管理用户信息 1.1 定义store和reducer src/store/userReducer.ts代码如下所示: import { createSlice…...
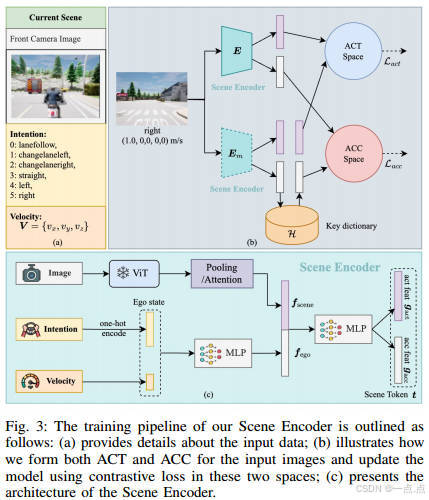
LeapVAD:通过认知感知和 Dual-Process 思维实现自动驾驶飞跃——论文阅读
《LeapVAD: A Leap in Autonomous Driving via Cognitive Perception and Dual-Process Thinking》2025年1月发表,来自浙江大学、上海AI实验室、慕尼黑工大、同济大学和中科大的论文。 尽管自动驾驶技术取得了显著进步,但由于推理能力有限,数…...

windows 部署 Kafka3.x KRaft 模式 不依赖 ZooKeeper
1.下载 https://archive.apache.org/dist/kafka/3.9.0/kafka_2.12-3.9.0.tgz2.配置使用 KRaft 模式 2.1 修改 Kafka 的配置文件 cd D:\data\bigdata\kafka_2.12-3.9.0\config\kraft 修改 server.properties # 设置 Kafka 数据日志存储目录 log.dirsD:\\data\\bigdata\\kaf…...
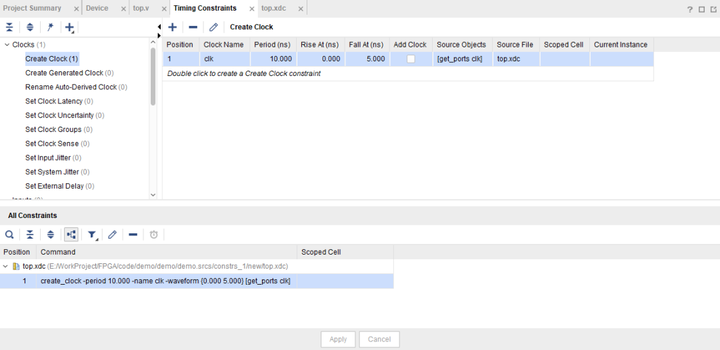
Xilinx FPGA | 管脚约束 / 时序约束 / 问题解析
注:本文为 “Xilinx FPGA | 管脚约束 / 时序约束 / 问题解析” 相关文章合辑。 略作重排,未整理去重。 如有内容异常,请看原文。 Xilinx FPGA 管脚 XDC 约束之:物理约束 FPGA技术实战 于 2020-02-04 17:14:53 发布 说明&#x…...

Python-JsonRPC
Python-JsonRPC 使用Python学习JsonRPC数据交互 1-核心知识点 1)什么是JsonRPC,这种协议是如何工作的?->使用请求进行验证2)JsonRPC可以使用Postman进行验证吗?->可以使用POSTMAN进行调用(使用HTTP请…...

Redis从入门到实战——实战篇(下)
四、达人探店 1. 发布探店笔记 探店笔记类似于点评网站的评价,往往是图文结合。对应的表有两个: tb_blog:探店笔记表,包含笔记中的标题、文字、图片等tb_blog_comments:其他用户对探店笔记的评价 步骤①࿱…...

面试问题(连载。。。。)
flexbox 和 crid 的区别 1. 布局维度与核心特性 Flexbox(弹性盒子) 一维布局:专注于行或列的线性排列,适合单方向(水平或垂直)的布局需求。动态分配空间:通过 flex-grow、flex-shrink 和 flex…...

springboot项目tomcat中加载不了
Spring Boot项目在Tomcat中加载不了的问题可能由多种原因引起,包括打包方式不正确、依赖配置错误、启动类配置不当等。以下是详细的解决方案: 1. 修改项目打包形式 将项目打包形式从jar改为war,以确保项目以正确的格式被Tomcat加载。在pom.…...

venv和pyenv在mac上
是的,理论上你可以用 venv 选择 Python 版本,但有一个关键前提:系统中必须已安装该版本的 Python 解释器。venv 本身并不提供 Python 版本管理功能,它只是基于现有的 Python 环境创建虚拟隔离空间。以下分场景详细说明:…...

OpenCv实战笔记(1)在win11搭建opencv4.11.1 + qt5.15.2 + vs2019_x64开发环境
一. 准备工作 Visual Studio 2019(安装时勾选 C 桌面开发 和 Windows 10 SDK) CMake 3.20(官网下载) Qt 5.15.2(下载 Qt Online Installer)安装时勾选 MSVC 2019 64-bit 组件。 opencv 4.11.1 源码下载 git…...

前端获取流式数据并输出
在一些实时对话、日志推送等场景下,如果使用传统一次性加载数据的方式,可能会出现等待时间较长的不友好交互,这个时候我们需要使用流式布局分段获取数据,渐进式加载,减少等待焦虑。 原生js上,我们使用fetch…...

全局网络:重构数字时代的连接范式
从局部到全局 —— 网络架构的范式革命 在全球化与数字化深度融合的今天,传统网络架构的 “碎片化” 问题日益凸显:跨地域数据流通低效、设备互联孤岛化、安全策略难以统一。 全局网络作为一种突破地域与技术边界的新型网络架构,正成为企业…...

C++ Primer (第五版)-第十四章重载运算与类型转换
文章目录 一、基本概念可以被重载某些运算符不应被重载尽量明智使用运算符重载赋值和复合赋值运算符选择作为成员或者非成员 输入和输出运算符输入运算符尽量减少格式化操作输入输出运算符必须是非成员函数 重载输入运算符>>输入时的错误标示错误 算数和关系运算符相等运…...

nt!MiSessionAddProcess函数分析和nt!MmSessionSpace全局变量的关系
第一部分: 1: kd> g Breakpoint 42 hit nt!MiSessionAddProcess: 80ab2fbe 55 push ebp 1: kd> kc # 00 nt!MiSessionAddProcess 01 nt!MmCreateProcessAddressSpace 02 nt!PspCreateProcess 03 nt!NtCreateProcessEx 04 nt!_KiSystemServic…...

鸿蒙开发——5.ArkUI @Builder装饰器:打造高效可复用的UI组件
鸿蒙开发——5.ArkUI Builder装饰器:打造高效可复用的UI组件 ArkUI Builder装饰器:打造高效可复用的UI组件一、Builder装饰器是什么?二、两种构建函数类型1. 私有自定义构建函数2. 全局自定义构建函数 三、参数传递核心规则1. 按值传递&#…...

bash和zsh的区别
Bash(Bourne-Again SHell)和 Zsh(Z Shell)都是 Unix/Linux 系统中的主流 Shell,但它们在功能、配置和用户体验上有显著区别。以下是两者的详细对比: 1. 历史与兼容性 特性BashZsh诞生时间1989 年ÿ…...

PyTorchVideo实战:从零开始构建高效视频分类模型
视频理解作为机器学习的核心领域,为动作识别、视频摘要和监控等应用提供了技术基础。本教程将详细介绍如何利用PyTorchVideo和PyTorch Lightning两个强大框架,构建基于Kinetics数据集训练的3D ResNet模型,实现高效的视频分类流程。 PyTorch…...

深入理解Spring缓存注解:@Cacheable与@CacheEvict
在现代应用程序开发中,缓存是提升系统性能的重要手段。Spring框架提供了一套简洁而强大的缓存抽象,其中Cacheable和CacheEvict是两个最常用的注解。本文将深入探讨这两个注解的工作原理、使用场景以及最佳实践。 1. Cacheable注解 基本概念 Cacheable…...

Rust 与 Golang 深度对决:从语法到应用场景的全方位解析
一、引言 在软件开发的快速发展浪潮中,Rust 和 Golang(Go 语言)脱颖而出,成为开发者热议的编程语言。Rust 凭借强大的内存安全性与卓越的性能备受赞誉,Golang 则以简洁的语法和出色的并发处理能力赢得开发者青睐。本文…...

java加强 -泛型
概念 定义类、接口、方法时,同时声明了一个或多个类型变量(如<E>),称为泛型类、泛型接口、泛型方法、它们统称为泛型。 语法 public class ArrayList<E>{} E可以接收不同类型的数据,可以是字符串&…...

pygame联网飞机大战游戏实现
客户端 import pygame import socket import json import threadingclass GameClient:def __init__(self):pygame.init()self.screen_width 600 # 宽度减小self.screen_height 800 # 高度增加self.screen pygame.display.set_mode((self.screen_width, self.screen_heigh…...

SEMI E40-0200 STANDARD FOR PROCESSING MANAGEMENT(加工管理标准)-(二)
8 行为规范 8.1 本章定义监督实体(Supervisor)与加工资源(Processing Resource)为实现物料加工所需的高层级通信逻辑,不涉及具体消息细节(详见第10章消息服务)。 8.2 加工任务通信 8.2.1 加工…...

根据窗口大小自动调整页面缩放比例,并保持居中显示
vue 项目 直接上代码 图片u1.png 是个背景图片 图片u2.png 是个遮罩 <template><div id"app"><div class"viewBox"><divclass"screen":style"{ transform: translate(-50%,-50%…...

如何在Jmeter中调用C程序?
在JMeter中调用C语言程序可以通过以下几种方式实现: 方法一:使用OS Process Sampler JMeter的“OS Process Sampler”可以用来调用外部程序,包括C语言编写的可执行文件。 步骤: 准备C语言程序: 编写C语言代码并编译…...

Android SDK 国内镜像及配置方法(2025最新,包好使!)
2025最新android sdk下载配置 1、首先你需要有android sdk manager2、 直接上教程修改hosts文件配置域名映射即可(不用FQ)2.1 获取ping dl.google.com域名ip地址2.2 配置hosts文件域名映射2.3 可以随意下载你需要的sdk3、 总结:走过弯路,踩过坑!!!大家就不要踩了!避坑1…...

【Python开源】深度解析:一款高效音频封面批量删除工具的设计与实现
🎵 【Python开源】深度解析:一款高效音频封面批量删除工具的设计与实现 🌈 个人主页:创客白泽 - CSDN博客 🔥 系列专栏:🐍《Python开源项目实战》 💡 热爱不止于代码,热情…...

OpenStack Yoga版安装笔记(26)实例元数据笔记
一、实例元数据概述 1.1 元数据 (官方文档:Metadata — nova 25.2.2.dev5 documentation) Nova 通过一种叫做元数据(metadata)的机制向其启动的实例提供配置信息。这些机制通常通过诸如 cloud-init 这样的初始化软件…...
