数据结构 集合类与复杂度

📕1. 集合类

Java 集合框架（Java Collection Framework）又被称容器，是定义在java.util包下的一组接口和其实现类。用于将大量的数据置于一个单元中，进行高效的增删改查。

Java中的抽象类，就是抽象的数据结构对应的具体实现。

• Collection ：是一个接口，包含了大部分容器常用的⼀些⽅法
• List : 是⼀个接口，规范了ArrayList 和 LinkedList中要实现的方法
  1.ArrayList : 顺序表
  2.LinkedList : 链表
• Stack : 栈，一种特殊的顺序表
• Queue ：队列，一种特殊的顺序表
• HashSet / HashMap ：哈希表
• TreeSet / TreeMap : 二叉树
• Priorityqueue ：优先级队列 / 堆

📕2. 时间复杂度

引言 ：我们该如何衡量一个算法的好坏呢？衡量的标准是什么呢？所以，我们为了衡量算法的好坏不得不引入“算法效率”这个词。算法效率又分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作空间复杂度。 时间复杂度主要衡量的是⼀个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间。

✏️2.1 时间复杂度

算法中的基本操作的执行次数，为算法的时间复杂度。

✏️2.2 大O渐进表示法

请计算一下 func1 基本操作执行了多少次？

void func1(int N){int count = 0;for (int i = 0; i < N ; i++) {for (int j = 0; j < N ; j++) {count++;}}for (int k = 0; k < 2 * N ; k++) {count++;}int M = 10;while ((M--) > 0) {count++;}System.out.println(count);}

从数学角度分析，我们可以把形参看做成问题规模N，我们要计算操作次数和问题规模N的函数关系。

答 ：func1执行的基本操作次数：

F(N) = N^2 + 2*N + 10

当 N = 10 时 ：F（N）= 130
当 N = 100 时 ：F（N）= 10210
当 N = 1000 时 ：F（N）= 1002010

我们可以发现，随着N越来越大，基本操作的执行顺序就越来越相近。所以我们算时间复杂度时，并不一定要计算具体的执行次数，只需要计算大致的执行次数即可。那么这⾥我们使用大O渐进表示法。

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

大O渐进表示法原则：将问题规模N与操作次数的函数关系只取最高次项，其他项忽略掉，将最高次项前系数也去掉，用 O() 表示。 （🌰举个例子：假如你花一百万零两千块买了一套房子，当别人问你房子多少钱买的时候，你只需要说一百万买的就行，不用刻意强调那两千元）

例如：上述代码的时间复杂度就可以表示为O（N）

✏️2.3 常见的时间复杂度量级

• 常数阶 O(1)
• 对数阶 O(logN)
• 线性阶 O(n)
• 线性对数阶 O(nlogN)
• 平方阶 O(n^2)
• 立方阶 O(n^3)
• 指数阶 (2^n)

常见的时间复杂度关系图象：

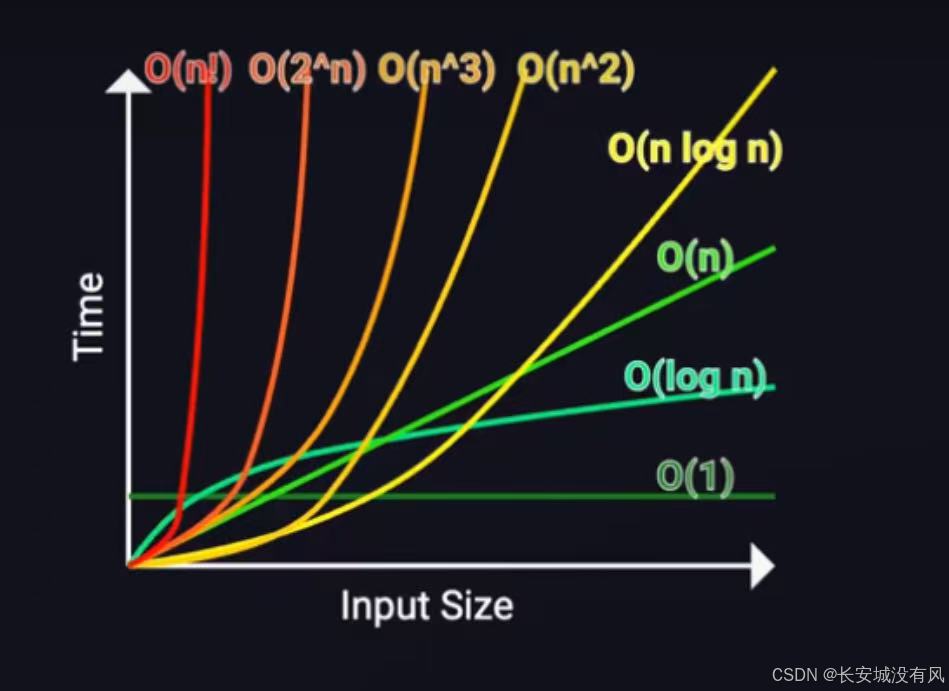
有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：输入任意规模的最大运行次数
最好情况：输入任意规模的最小运行次数

例如：在⼀个长度为N数组中搜索⼀个数据x
最好情况：1次找到
最坏情况：N次找到
在实际中⼀般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

✏️2.4 常见时间复杂度计算举例

计算时间复杂度，一定要先找到基本操作是啥。（打印，修改，比较，删除等）

实例1：

// 计算func2的时间复杂度？
void func2(int N) {int count = 0;for (int k = 0; k < 2 * N ; k++) {count++;}int M = 10;while ((M--) > 0) {count++;}System.out.println(count);
}

时间复杂度为O（N）

实例2：

//计算func3的时间复杂度
void func3(int N, int M) {int count = 0;for (int k = 0; k < M; k++) {count++;}for (int k = 0; k < N ; k++) {count++;}System.out.println(count);
}

时间复杂度为O（M+N）（无法判断M和N谁大谁小）

描述问题规模的方式不一定只有一个变量，可以有多个。

实例3：

// 计算func4的时间复杂度？
void func4(int N) {int count = 0;for (int k = 0; k < 100; k++) {count++;}System.out.println(count);
}

时间复杂度为O（1）

基本操作的执行次数和问题规模N无关，此代码中，无论N等于多少，count++都执行100次。假设此时K为1000000，时间复杂度也是O(1) ，O(1)和O(1)执行时间可能会差别很大。

时间复杂度衡量的是问题规模和时间的趋势变化，不能决定时间快慢。

实例4：

// 计算bubbleSort的时间复杂度？
void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}	}if (sorted == true) {break;}}
}

时间复杂度为O（N^2）

实例5：

// 计算binarySearch的时间复杂度？
public static int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;while (begin <= end) {int mid = begin + ((end-begin) / 2);if (array[mid] < value){begin = mid + 1;}else if (array[mid] > value){end = mid - 1;}else{return mid;}}return -1;
}

时间复杂度为O（logN）

实例6：

// 计算阶乘递归factorial的时间复杂度？
public static long factorial(int N) {return N < 2 ? N : factorial(N-1) * N;
}

时间复杂度为O（N）

虽然没有循环，但是有递归，理论上所有的递归都能写成循环。

实例7：

// 计算斐波那契递归fibonacci的时间复杂度？
public static int fibonacci(int N) {return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}

时间复杂度为O（2^N）

📕3. 空间复杂度

空间复杂度是对⼀个算法在运行过程中临时占用存储空间大小的量度。空间复杂度计算规则基
本跟时间复杂度类似，也使用大O渐进表示法。

实例1：

// 计算bubbleSort的空间复杂度？
void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}
}

空间复杂度为O（1）

给一个数组，长度为N，在后续并没有创造任何和空间，因为时间虽然是一去不复返的，但是空间是可以重复使用的。

实例2：

// 计算fibonacci的空间复杂度？
int[] fibonacci(int n) {long[] fibArray = new long[n + 1];fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; i++) {fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}

空间复杂度为O（N）

实例3：

// 计算阶乘递归Factorial的空间复杂度？
long factorial(int N) {return N < 2 ? N : factorial(N-1)*N;
}

空间复杂度为O（N）

递归在调用方法的过程中，也是需要消耗空间的，在JAVA代码中，方法之间的调用关系，会保存在“栈”内存区域中（栈是JVM内置的一个内存区域），方法调用时开辟空间，方法结束时销毁空间，递归调用了多少次，“栈”的最大消耗空间就是多少。