密码学--RSA
一、实验目的
1.随机生成明文和加密密钥
2.利用C语言实现素数选择(素性判断)的算法
3.利用C语言实现快速模幂运算的算法(模重复平方法)
4.利用孙子定理实现解密程序
5.利用C语言实现RSA算法
6.利用RSA算法进行数据加/解密
二、实验内容
1、题目内容描述
①实现快速模幂乘法计算ax mod m;
②实现Euclid算法计算gcd(a,b);
③随机生成正整数,用Miller_Rabin算法进行素性判断,安全参数t=10,得到通过检验的两个素数p和q,计算出n,φ(n),dp,dq和inv_p;
④实现扩展Euclid算法,当公钥e = 7时,计算出私钥d;
⑤随机生成明文数字,利用快速模幂乘法,计算出密文,利用孙子定理解密出明文。
2、关键代码的设计、实现与执行
设计思路:
先生成随机生成密钥以时间设置随机数生成器的种子,以确保每次运行程序时生成的随机数序列都是不同的。p大于 100确保p是一个足够大的素数;并调用最大公约数函数:gcd(),检查p-1和e的最大公约数为 1,即为了确保p和e是互质的;再调用primetest()函数,进行素性判断;rand()%Max是为了将随机生成的p,q控制在一定范围内,以免溢出int范围,关键代码如下:(此处只以p为例,在p生成后,以同样的方法生成q,只是换一个字母)
srand(time(NULL));//以时间为种子,以确保每次生成的随机数不同
do
{
if((p>100)&&(gcd(p-1,e)==1)&&(primetest(p,t)==1))//确保p足够大,且与e互质,并调用素性检验的函数,要求p为素数
break;//p满足上述条件则即可跳出循环
p=rand()%Max;//若p未满足上述条件则重新生成
}while(1);//只有在p到达条件成功生成后才会跳出循环
紧接着就是上面提到的计算最大公约数的函数,只要最大公约数为1,则证明两个数互质,关键代码如下:(也就是前面两个实验:仿射密码和希尔密码用到的求最大公约数的函数)
if(a<b)//交换数
{
temp=a;
a=b;
b=temp;
}
while(b!=0)
{
temp=a%b;
a=b;
b=temp;
}
return a;//得到最大公因数
然后是上面提到过的素性检验部分,t是实验题目中给出的安全参数,即实验t次,然后以r/2不断循环,在循环期间s++,r右移,再循环安全参数t次,检测传入的数x是否通过素性检测,这样检测q,p两个数,关键代码如下:
if(!(x&1))//检查 x 是否为偶数(只有偶数与1进行按位与操作结果才为0)。如果是偶数,函数返回 0,表示 x 不是质数
return 0;
while(!(r&1))// r 除以2的余数不为1。这意味着循环会一直执行直到 r 为奇数。
{
s++;
r>>=1;//在循环体内,首先 s 被增加1,然后 r 右移一位(相当于除以2)。这是在寻找 x 的位数。
}
for(i=0;i<t;i++)//安全参数t,则重复执行 t 次
{
a=rand()%(x-2)+2;//在循环体内,生成一个在[2, x-2] 范围内的随机整数并赋值给 a。
if(gcd(2,x)>1)//检查X是否数质数,2太小了,也排除在外
return 0;
int b=quickpower(a,r,x);//调用快速幂运算
if(b==1||b==x-1)//通过检测
continue;
for(j=0;j<s;j++)
{
b=b*b%x;
if(b==x-1)//通过检测
break;
}
if(j==s)//表示X不是质数
return 0;
}
return 1;
在已知当公钥e = 7时,计算出私钥d,上述已经得到了p,q,即可算出dn=(p-1)*(q-1),然后对计算出e模dn的逆元即是私钥d,关键代码如下:
int dn=(p-1)*(q-1);
int d=inverse_a(e,dn);
在加密解密的时候都运用了快速模幂算法,初始值为1,从指数二进制最低位开始,每步都把底数平方,遇到1就乘以底数,但是在快速模幂平方或者×原本的数的时候,由于p,q是两个大质数,所有有溢出风险,即再添加一个快速模乘的函数,代替快速模幂里面的乘法,关键代码如下:
快速模幂部分:
while(b)
{
if(b&1)//检查 b 的最后一位是否为 1;对于每一次循环,我们只对 b 的最后一位为 1 的情况进行处理,相当于每次只处理一个乘法结果。
ans=(ans+res)%c;
res=(res+res)%c;
b>>=1;//右移操作,将 b 的所有位向右移动一;在每次循环中处理的是 b 的下一位。
}
return (int)ans;//函数返回ans,即最终结果
快速模乘部分:
while(b!=0){
if((b&1)!=0)//检查 b 的最后一位是否为 1
{
ans=quickmultiply(ans,base,c);
}
base=quickmultiply(base,base,c);// base 自乘并对 c 取模
b>>=1;//右移操作,将 b 的所有位向右移动一;在每次循环中处理的是 b 的下一位。
}
return ans;
为了操作方便且不溢出,解密过程还使用了孙子定理加速解密过程,由于p,q是两个大质数,所以它们的欧拉函数就是本身减1,于是用得到的欧拉函数调用快速模幂算法的函数,得到x1和x2,
再代入式子即可得到解密后的明文,关键代码部分如下:
int dp=d%(p-1);
int dq=d%(q-1);
if(dp<0)
dp=dp+p-1;
if(dq<0)
dq=dq+q-1;//求得p,q的欧拉函数
int inv_p=inverse_a(p,q);
int inv_q=(1-p*inv_p)/q;
int c1=c%p;
int c2=c%q;
int x1=quickpower(c1,dp,p);
int x2=quickpower(c2,dq,q);//快速模幂分别求得两个x1,x2
cout<<1;
cout<<"inv_p="<<inv_p<<endl;
cout<<"inv_q="<<inv_q<<endl;
cout<<"x1="<<x1<<endl;
cout<<"x2="<<x2<<endl;
int m=(x1*q*inv_q+x2*p*inv_p)%n;//代入计算
结果截图如下:


- 实验结果分析
结果截图在上面过程中,可以看到每次生成的p,q都不同,且是大质数,,每次的明文也是随机生成的不同的数,可以看到过程,得到密文cipher,再经过一系列解密后得到解密后的明文,经观察可以看到,解密生成的密文与随机生成的明文是一致的,故可以得到加密解密过程正确。
三、实验思考
1、实验过程总结
相较于仿射密码和希尔密码,rsa密码算法更为复杂,虽然在这个实验中明文是数字而不是字母,需要转换,但是随机生成的p,q需要是大质数,无疑是增加了实验的难度。所以在随机生成了p,q后第一步要解决的难题就是素性检验的问题,根据理论知识,在安全参数为t的情况下,循环执行检查t次,每次随机生成范围内的数,看是否存在除1外的公因数;紧接着就是加密解密过程都涉及的快速模幂运算,将指数转换成二进制形式,从低位开始,不断平方右移,遇到1再乘底数,由于int类型的长度有限,所以在快速模幂运算中间的有两步乘法可能会出现溢出现象,可以将其改为加法,即快速模乘运算;最后的重点就是孙子定理,在解密中运用,加速解密,其中涉及到p,q的欧拉函数,将解密的式子分成两个式子减小运算量,最后再结合在一起,即得到加密过程。在前面两个实验的基础上,完成这个实验会较为轻松一点,无非就是多添了三个部分,但是此实验由于明文也是随机生成的,所以避免了文件操作。
- 回答实验指导书最后提出的问题
思考题1:
在这个思考题中可以看到其实就是借用了rsa算法中的快速模幂算法,按题目中已给出的n=101*157=15857,e=7,s0=2,于是得到下面的结果:

当然也可以更换题目中给出的初始值,如下:


思考题2:
在这个思考题中可以看到就是没有了解密部分,将铭文空间里的每一个数进行加密计算,看得到的结果是否和明文一致,一致就是不动点,操作结果如下:



相关文章:

密码学--RSA
一、实验目的 1.随机生成明文和加密密钥 2.利用C语言实现素数选择(素性判断)的算法 3.利用C语言实现快速模幂运算的算法(模重复平方法) 4.利用孙子定理实现解密程序 5.利用C语言实现RSA算法 6.利用RSA算法进行数据加/解密 …...

如何选择自己喜欢的cms
选择内容管理系统cms what is cms1.whatcms.org2.IsItWP.com4.Wappalyzer5.https://builtwith.com/6.https://w3techs.com/7. https://www.netcraft.com/8.onewebtool.com如何在不使用 CMS 检测器的情况下手动检测 CMS 结论 在开始构建自己的数字足迹之前,大多数人会…...

BUUCTF——杂项渗透之赛博朋克
下载附件,是一个txt。打开查看,数据如下: 感觉这个像是用十六进制编辑器打开后的图片数据。为了验证此想法,我用010editor打开,发现文件头的确是png图片的文件头。 把txt文件后缀改成png格式,再双击打开&am…...

【c++】 我的世界
太久没更新小游戏了 给个赞和收藏吧,求求了 要游戏的请私聊我 #include <iostream> #include <vector>// 定义世界大小 const int WORLD_WIDTH 20; const int WORLD_HEIGHT 10;// 定义方块类型 enum BlockType {AIR,GRASS,DIRT,STONE };// 定义世界…...

React 中集成 Ant Design 组件库:提升开发效率与用户体验
React 中集成 Ant Design 组件库:提升开发效率与用户体验 一、为什么选择 Ant Design 组件库?二、基础引入方式三、按需引入(优化性能)四、Ant Design Charts无缝接入图标前面提到了利用Redux提供全局维护,但如果在开发时再自己手动封装组件,不仅效率不高,可能开发的组件…...

HunyuanCustom, 腾讯混元开源的多模态定制视频生成框架
HunyuanCustom是一款由腾讯混元团队开发的多模态驱动定制视频生成框架,能够支持图像、音频、视频和文本等多种输入方式。该框架专注于生成高质量的视频,能够实现特定主体和场景的精准呈现。 HunyuanCustom是什么 HunyuanCustom是腾讯混元团队推出的一种…...

Lightweight App Alternatives
The tech industry’s business model thrives on constant churn: new features, fancier designs, and heavier apps — not because they’re essential, but because they keep consumers upgrading. Stripping your phone back to basics is an act of tech self-defense.…...

STM32F103RCT6 + MFC实现网口设备搜索、修改IP、固件升级等功能
资源下载链接:https://download.csdn.net/download/qq_35831134/90712875?spm=1001.2014.3001.5501 一.大概逻辑: // 网口搜索大概逻辑: // ************************************************************************** // 一.环境: // 上位机用MFC下位机用STM32F103R…...

编译原理实验 之 语法分析程序自动生成工具Yacc实验
文章目录 实验环境准备复现实验例子分析总的文件架构实验任务 什么是Yacc Yacc(Yet Another Compiler Compiler)是一个语法分析程序自动生成工具,Yacc实验通常是在编译原理相关课程中进行的实践项目,旨在让学生深入理解编译器的语法分析阶段以及掌握Yac…...

[250504] Moonshot AI 发布 Kimi-Audio:开源通用音频大模型,驱动多模态 AI 新浪潮
目录 Moonshot AI 发布 Kimi-Audio:开源音频基础模型,赋能音频理解、生成与对话新时代核心能力与特性技术基础开放资源与评估行业意义 Moonshot AI 发布 Kimi-Audio:开源音频基础模型,赋能音频理解、生成与对话新时代 Moonshot A…...

从“山谷论坛”看AI七剑下天山
始于2023年的美国山谷论坛(Hill and Valley Forum)峰会,以“国会山与硅谷”命名,寓意连接科技界与国家安全战略。以人工智能为代表的高科技,在逆全球化时代已成为大国的致胜高点。 论坛创办者Jacob Helberg,现在是华府的副国务卿,具体负责经济、环境和能源事务。早先曾任…...

C——数组和函数实践:扫雷
此篇博客介绍用C语言写一个扫雷小游戏,所需要用到的知识有:函数、数组、选择结构、循环结构语句等。 所使用的编译器为:VS2022。 一、扫雷游戏是什么样的,如何玩扫雷游戏? 如图,是一个标准的扫雷游戏初始阶段。由此…...

sui在windows虚拟化子系统Ubuntu和纯windows下的安装和使用
一、sui在windows虚拟化子系统Ubuntu下的安装使用(WindowsWsl2Ubuntu24.04) 前言:解释一下WSL、Ubuntu的关系 WSL(Windows Subsystem for Linux)是微软推出的一项功能,允许用户在 Windows 系统中原生运行…...

智能合约在去中心化金融(DeFi)中的核心地位与挑战
近年来,区块链技术凭借其去中心化、不可篡改等特性,在全球范围内掀起了技术革新浪潮。去中心化金融(DeFi)作为区块链技术在金融领域的重要应用,自 2018 年以来呈现出爆发式增长态势。据 DeFi Pulse 数据显示࿰…...

Femap许可使用数据分析
在当今竞争激烈的市场环境中,企业对资源使用效率和成本控制的关注日益增加。Femap作为一款业界领先的有限元分析软件,其许可使用数据分析功能为企业提供了深入洞察和智能决策的支持。本文将详细介绍Femap许可使用数据分析工具的特点、优势以及如何应用这…...

有关SOA和SpringCloud的区别
目录 1. 定义 2. 架构风格 3. 技术栈 4. 服务交互 5. 适用场景 前言 面向服务架构(SOA)是一种软件设计风格,它将应用程序的功能划分为一系列松散耦合的服务。这些服务可以通过标准的通信协议进行交互,通常是HTTP或其他消息传…...

学习搭子,秘塔AI搜索
什么是秘塔AI搜索 《秘塔AI搜索》的网址:https://metaso.cn/ 功能:AI搜索和知识学习,其中学习部分是亮点,也是主要推荐理由。对应的入口:https://metaso.cn/study 推荐理由 界面细节做工精良《今天学点啥》板块的知…...

IBM BAW(原BPM升级版)使用教程第六讲
续前篇! 一、事件:Undercover Agent 在 IBM Business Automation Workflow (BAW) 中,Undercover Agent (UCA) 是一个非常独特和强大的概念,旨在实现跨流程或系统的事件处理和触发机制。Undercover Agent 主要用于 事件驱动的流程…...

高并发PHP部署演进:从虚拟机到K8S的DevOps实践优化
一、虚拟机环境下的部署演进 1. 低并发场景(QPS<10)的简单模式 # 典型部署脚本示例 ssh userproduction "cd /var/www && git pull origin master" 技术痛点: 文件替换期间导致Nginx返回502错误(统计显示…...
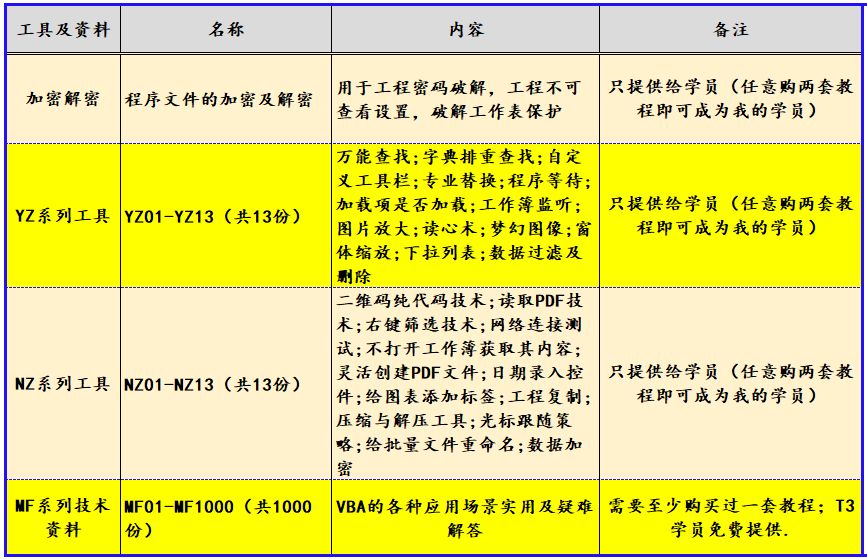
VBA高级应用30例应用4:利用屏蔽事件来阻止自动运行事件
《VBA高级应用30例》(版权10178985),是我推出的第十套教程,教程是专门针对高级学员在学习VBA过程中提高路途上的案例展开,这套教程案例与理论结合,紧贴“实战”,并做“战术总结”,以…...

Centos 7.6 安装 Node.js 20 的环境配置记录
Centos 7.6 安装 Node.js 20 的环境配置记录 Centos 7在 2024 年的 6 月 30 号已经停止维护了,但是由于时代原因,很多服务还是跑在这个系统上。本篇博文记录如何在 Centos 7.6 上安装 Node20。 初步安装 node 下载 node.js 的 Linux 版本 cd ~ curl -O h…...

springboot3 + mybatis-plus3 创建web项目实现表增删改查
Idea创建项目 环境配置说明 在现代化的企业级应用开发中,合适的开发环境配置能够极大提升开发效率和应用性能。本文介绍的环境配置为: 操作系统:Windows 11JDK:JDK 21Maven:Maven 3.9.xIDE:IntelliJ IDEA…...

每天批次导入 100 万对账数据到 MySQL 时出现死锁
一、死锁原因及优化策略 1.1 死锁原因分析 批量插入事务过大: Spring Batch 默认将整个 chunk(批量数据块)作为一个事务提交,100 万数据可能导致事务过长,增加锁竞争。 并发写入冲突: 多个线程或批处理作…...

【人工智能学习之动作识别TSM训练与部署】
【人工智能学习之动作识别TSM训练与部署】 基于MMAction2动作识别项目的开发一、MMAction2的安装二、数据集制作三、模型训练1. 配置文件准备2. 关键参数修改3. 启动训练4. 启动成功 ONNX模型部署方案一、环境准备二、执行转换命令 基于MMAction2动作识别项目的开发 一、MMAct…...

ES6/ES11知识点 续五
迭代器【Iterator】 ES6 中的**迭代器(Iterator)**是 JavaScript 的一种协议,它定义了对象如何被逐个访问。迭代器与 for…of、扩展运算符、解构赋值等语法密切相关。 📘 迭代器工作原理 ES6 迭代器的工作原理基于两个核心机制…...

sqli-labs靶场18-22关(http头)
目录 less18(user-agent) less19(referer) less20(cookie) less21(cookie) less22(cookie) less18(user-agent) 这里尝试了多次…...

redhat9 安装pywinrm
看了很多文档,都是有很多限制,还是老老实实用pip 安装: Step1: 安装pip: [rootip-abc ~]# python get-pip.py Collecting pip Downloading pip-25.1.1-py3-none-any.whl.metadata (3.6 kB) Collecting wheel Downloading wheel-0.45.1-py…...

Android系统架构模式分析
本文系统梳理Android系统架构模式的演进路径与设计哲学,希望能够借此探索未来系统的发展方向。有想法的同学可以留言讨论。 1 Android层次化架构体系 1.1 整体分层架构 Android系统采用五层垂直架构,各层之间通过严格接口定义实现解耦: 应用…...

Web前端VSCode如何解决打开html页面中文乱码的问题(方法2)
Web前端—VSCode如何解决打开html页面中文乱码的问题(方法2) 1.打开VScode后,依次点击 文件 >> 首选项 >> 设置 2.打开设置后,依次点击 文本编辑器 >> 文件(或在搜索框直接搜索“files.autoGuessEnc…...

【NextPilot日志移植】logged_topics.cpp解析
📘 PX4 Logger 模块注册 uORB 主题、实际订阅与数据采集流程 🧭 目的与背景 在 PX4 飞控中,日志记录模块 logger 需要记录多个 uORB 主题的数据(如 IMU、GPS、姿态等)。为了系统统一管理这些记录需求,log…...
