【日撸 Java 三百行】Day 7(Java的数组与矩阵元素相加)
目录
Day 7:Java 的数组与矩阵元素相加
一、基本知识
二、矩阵的建立与基本计算
三、代码及测试
拓展:Arrays类详解
小结
Day 7:Java 的数组与矩阵元素相加
Task:
- 矩阵的赋值.
- 二重循环.
一、基本知识
在学习 Java 中的数组与矩阵前,我们需要以下两个基本知识:
- 动态创建
- Arrays 类
这部分的知识点请参考相关的 Java 专题补充:
二、矩阵的建立与基本计算
本博客中,将用代码实现两种基本的矩阵计算:全元素求和,基本加法
1. 矩阵元素总和
同样的,我们依旧把这个功能封装为单独的函数
/************************ Sum the elements of a matrix.* * @param paraMatrix The given matrix.* @return The sum of all its elements.**********************/public static int matrixElementSum(int[][] paraMatrix) {int resultSum = 0;for (int i = 0; i < paraMatrix.length; i++) {for (int j = 0; j < paraMatrix[0].length; j++) {resultSum += paraMatrix[i][j];} // Of for j} // Of for ireturn resultSum;}// Of matrixElementSum
代码不多做解释,通过双层 for 循环即能遍历矩阵中的所有元素。唯一值得注意的是,我们该如何去理解通过数组组成的矩阵?
首先矩阵的高其实就是矩阵的一维部分,一个矩阵在计算机中可以看做是“一维数列”的数组,把这个数组的元素纵向放置就构成了我们视觉可见的一个“矩形”的数字阵列。而这个“一维数列”的数组的长度自然就是这个阵列的纵向长度,也就是高,是把这个数组的元素纵向放置可以排的行数。因此:
paraMatrix.length
就是矩阵的宽,或者说行数。
同理,“一维数列”的数组中的每个元素都是一个一维数列,每个数列的长度就构成了矩阵的长,或者说列数。实际代码中,我们取出“一维数列”的数组的第一个元素,也就是矩阵的第一行,并求这一个行的长度即可:
paraMatrix[0].length
具体遍历的话,基本所有语言的二维存储都是采用行优先的存储,而普遍的遍历都是先行后列的遍历思想,因此这一点不再赘述。
2. 矩阵相加
一个优秀的程序是需要有自我报错能力的,比如这里的非法矩阵相加。
矩阵相加的话需要符合线性代数中矩阵计算的一个基本要求——即相加的双方矩阵必须是同型的。因此注意对于非法情况的判断。
/************************ Add two matrices. Attention: No error check is provided at this moment.* * @param paraMatrix1 The first matirx.* @param paraMatrix2 The second matrix. It should have the same size as the* first one's* @return The addition of these matrices.**********************/public static int[][] matrixAddition(int[][] paraMatrix1, int[][] paraMatrix2) {if(paraMatrix1.length!=paraMatrix2.length || paraMatrix1[0].length!=paraMatrix2[0].length) {System.out.println("Error! Two matrixs must have same height and width! ");}int[][] resultMatrix = new int[paraMatrix1.length][paraMatrix1[0].length];for (int i = 0; i < paraMatrix1.length; i++) {for (int j = 0; j < paraMatrix1[0].length; j++) {resultMatrix[i][j] = paraMatrix1[i][j] + paraMatrix2[i][j];} // Of for j} // Of for ireturn resultMatrix;}// Of matroxAddition
三、代码及测试
package basic;import java.util.Arrays;/*** This is the seventh code. Names and comments should follow my style strictly.** @author: Changyang Hu joe03@foxmail.com* @date created: 2025-05-09*/
public class MatrixAddition {/************************* @Title: main* @Description: The entrance of the program.** @param args Not used now.* @return void************************/public static void main(String args[]) {matrixElementSumTest();matrixAdditionTest();}// Of main/************************* * @Title: matrixElementSun* @Description: Sum the elements of a matrix** @param paraMatrix The given matrix* @return * @return int************************/public static int matrixElementSum(int[][] paraMatrix) {int resultSum = 0;for (int i = 0; i < paraMatrix.length; i++) {for (int j = 0; j < paraMatrix[0].length; j++) {resultSum += paraMatrix[i][j];} // Of for j} // Of for ireturn resultSum;}// Of matrixElementSum/*** ********************** @Title: matrixElementSumTest* @Description: Unit test for respective method.* * @return void **********************/public static void matrixElementSumTest() {int[][] tempMatrix = new int[3][4];for (int i = 0; i < tempMatrix.length; i++) {for (int j = 0; j < tempMatrix[0].length; j++) {tempMatrix[i][j] = i * 10 + j;} // Of for j} // Of for iSystem.out.println("The matrix is: \r\n" + Arrays.deepToString(tempMatrix));System.out.println("The matrix element sum is: " + matrixElementSum(tempMatrix) + "\r\n");}// Of matrixElementSumTest/*** ********************** @Title: matrixAddition* @Description: Add two matrices. Attention: NO error check is provided at this moment.** @param paraMatrix1 The first matrix.* @param paraMatrix2 The second matrix. It should have the same size as* the first one's.* @return The addition of these matrices.* @return int[][] **********************/public static int[][] matrixAddition(int[][] paraMatrix1, int[][] paraMatrix2) {int[][] resultMatrix = new int[paraMatrix1.length][paraMatrix1[0].length];for (int i = 0; i < paraMatrix1.length; i++) {for (int j = 0; j < paraMatrix1[0].length; j++) {resultMatrix[i][j] = paraMatrix1[i][j] + paraMatrix2[i][j];} // Of for j} // Of for ireturn resultMatrix;}// Of matrixAdditon/*** ********************** @Title: matrixAdditionTest* @Description: Unit test for respective method.* * @return void **********************/public static void matrixAdditionTest() {int[][] tempMatrix = new int[3][4];for (int i = 0; i < tempMatrix.length; i++) {for (int j = 0; j < tempMatrix[0].length; j++) {tempMatrix[i][j] = i * 10 + j;} // Of for j} // Of for iSystem.out.println("The matrix is; \r\n" + Arrays.deepToString(tempMatrix));int[][] tempNewMatrix = matrixAddition(tempMatrix, tempMatrix);System.out.println("The new matrix is: \r\n" + Arrays.deepToString(tempNewMatrix));}// Of matrixAdditionTest}// Of class MatricAddtion
运行结果如下:

拓展:Arrays类详解
【Java 专题补充】Arrays类详解-CSDN博客
小结
java提供了许多的库,而这些库方法能对一些基本的操作进行优化。本篇的矩阵相加并不是很难的一部分,但是却暗示了不同语言的实现思路,不同语言对于数组的声明以及遍历的策略。
另外本文提到的矩阵也是一种非常重要的数据结构,虽然许多语言对于矩阵实现封装库信息很有限(除开matlab这种从矩阵角度出发的编程语言),但是其包含的算法却仍然非常丰富。在 C,C++,java,python 中都有对应的用于处理矩阵数据的库,这些能为我们提供极大的便捷。因此基于基础的二维数组数据模拟复杂的矩阵算法能极大锻炼我们的代码思维与对矩阵之中包含的数学逻辑的理解。但需要注意的是,在使用这些现成的函数时,要有意识的去理解背后的原理,否则只会成为空有其表的调包侠。
同时,对于图像的颜色,在计算机中我们常用0-255的数值来表示。所以,一张图像实际上就是一个二维矩阵。这个基础使得矩阵在计算机视觉中的应用中也扮演着关键作用,其中延伸出来的图像处理算法也在继续为后世服务。
相关文章:

【日撸 Java 三百行】Day 7(Java的数组与矩阵元素相加)
目录 Day 7:Java 的数组与矩阵元素相加 一、基本知识 二、矩阵的建立与基本计算 三、代码及测试 拓展:Arrays类详解 小结 Day 7:Java 的数组与矩阵元素相加 Task: 矩阵的赋值.二重循环. 一、基本知识 在学习 Java 中的数组与矩…...

【Python】常用命令提示符
Python常用的命令提示符 一、Python环境基础命令【Windows】 于Windows环境下,针对Python,在CMD(命令提示符)常用的命令以及具体用法,怎么用; 主要包含:运行脚本、包管理、虚拟环境、调试与…...
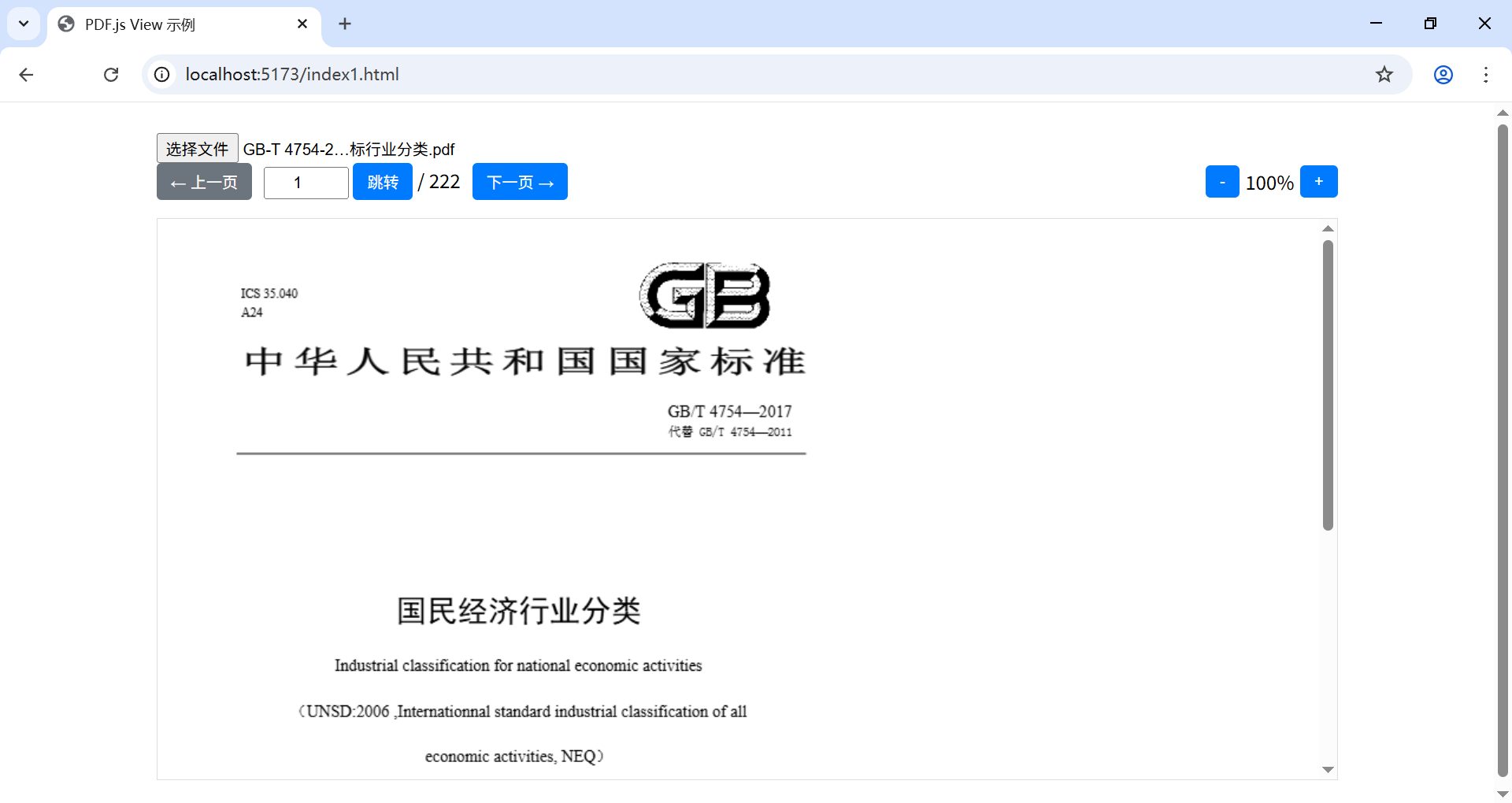
vite:npm 安装 pdfjs-dist , PDF.js View 预览功能示例
pdfjs-dist 是 Mozilla 的 PDF.js 库的预构建版本,能让你在项目里展示 PDF 文件。下面为你介绍如何用 npm 安装 pdfjs-dist 并应用 pdf.js 和 pdf.worker.js。 为了方便,我将使用 vite 搭建一个原生 js 项目。 1.创建项目 npm create vitelatest pdf-v…...

【开源版】likeshop上门家政系统PHP版全开源+uniapp前端
一.系统介绍 likeshop_上门家政系统,PHP版本更新至2.1.1最新版,全开源,适用于上门家政场景,系统拥有用户端、师傅端、无论运营还是二开都是性价比极高的100%开源家政系统。 二.搭建环境-教程 系统环境:CentOS、 运行…...
(已不推荐使用deprecated,建议使用img、video、audio标签))
html object标签介绍(用于嵌入外部资源通用标签)(已不推荐使用deprecated,建议使用img、video、audio标签)
文章目录 HTML <object> 标签详解基本语法与核心属性关键属性解析1. **data**2. **type**3. **width & height**4. **name** 嵌入不同类型的资源1. **嵌入图像**2. **嵌入音频**3. **嵌入视频**4. **嵌入 PDF** 参数传递与回退内容**参数(<param>&a…...

MySQL 8.0 OCP 英文题库解析(一)
Oracle 为庆祝 MySQL 30 周年,从 2025.04.20 ~ 2025.07.31 之间,所有人均可以免费考取 MySQL OCP 认证。从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证,省1700多RMB&…...

路由器断流排查终极指南:从Ping测试到Wireshark抓包5步定位法
测试路由器是否出现“断流”(网络连接间歇性中断),需通过多维度排查硬件、软件及外部干扰因素。以下是详细步骤指南: 一、基础环境准备 设备连接 有线测试:用网线将电脑直接连接路由器LAN口,排除WiFi干扰。…...

【Python零基础入门系列】第1篇:Python 是什么?怎么装环境?推荐哪些 IDE?
各位网友们,欢迎来到我的 Python 学习专栏! 前两天看到新闻英伟达为 CUDA 添加原生 Python 支持,意味着开发者可直接用 Python 操作 GPU,加速 AI 和高性能计算,降低门槛,让 Python 的应用范围更广、能力更强。 一直想写一系列文章教知友们从零开始学会 Python 编程,目…...

Spring Boot3 实现定时任务 每10分钟执行一次,同时要解决分布式的问题 区分不同场景
在Spring Boot 3中实现分布式定时任务,确保多实例环境下任务仅执行一次,可以采用以下方案: 方案一:Redis分布式锁(推荐) import org.springframework.data.redis.core.StringRedisTemplate; import org.sp…...

04 基于 STM32 的时钟展示程序
前言 我们经常会看到 各个场合下面有 基于数码管 的时钟程序 比如 在车站, 教室, 办公室 等等 各个场合都有 然后 这里就是做一个 简单的 时钟程序 展示程序 测试用例 每一秒钟更新时间, 然后 迭代更新 天, 时, 分 等等 然后 主流程 基于 天, 时分秒 渲染数码管 #incl…...

n8n工作流自动化平台:生成图文并茂的分析报告之Merge节点详细说明
1.成果展示 1.1工作流示意图 1.2成果 数据都是造得 2Merge节点 2.1Mode 通过选择模式指定合并节点应如何组合来自不同数据流的数据 2.1.1Append 保存所有输入的数据。选择一个输入数量,逐一输出每个输入的项目。节点等待所有连接的输入的执行。 2.1.2Combine 2.1.2.1Co…...

华为设备MSTP
一、MSTP核心理论 1. 基本概念 MSTP定义:MSTP(Multiple Spanning Tree Protocol)是一种基于实例的生成树协议,支持多个生成树实例(MSTI),每个实例对应一组VLAN,实现不同VLAN流量的负…...
系统软件部署全攻略:Redis、RabbitMQ、MySQL 等集群搭建指南)
华为银河麒麟 V10(ARM)系统软件部署全攻略:Redis、RabbitMQ、MySQL 等集群搭建指南
一、Redis 集群部署(主从 哨兵模式) 1. 环境准备 系统:华为银河麒麟 V10(ARM64)节点:3 台服务器(1 主 2 从 3 哨兵) 2. 安装包下载 bash # 华为镜像站 wget https://update.c…...

Loly: 1靶场渗透
Loly: 1 来自 <Loly: 1 ~ VulnHub> 1,将两台虚拟机网络连接都改为NAT模式 2,攻击机上做namp局域网扫描发现靶机 nmap -sn 192.168.23.0/24 那么攻击机IP为192.168.23.182,靶场IP192.168.23.241 3,对靶机进行端口服务探测 n…...

Linux系统入门第十一章 --Shell编程之函数与数组
一、Shell函数 1、函数的用法 Shell函数可用于存放一系列的指令。在Shell脚本执行的过程中,函数被置于内存中,每次调用函数时不需要从硬盘读取,因此运行的速度比较快。在Shell编程中函数并非是必须的元素,但使用函数可以对程序进…...

AWS VPC架构师指南:从零设计企业级云网络隔离方案
一、VPC核心概念解析 1.1 核心组件 VPC:逻辑隔离的虚拟网络,可自定义IPv4/IPv6地址范围(CIDR块) 子网(Subnet): 公有子网:绑定Internet Gateway(IGW)&#…...
聊聊自动化办公未来趋势
1. 自动化办公未来趋势 1.1 智能化与AI融合加深 随着人工智能技术的不断成熟,其在自动化办公中的应用将更加广泛和深入。未来,办公软件将具备更强的智能交互能力,能够理解自然语言指令,自动完成复杂的任务,如文档编辑…...

Flutter 异步原理-Zone
前言 Zone 是 Dart 异步模型中的核心机制,主要用于: 隔离异步上下文,形成逻辑上的执行环境。捕获未处理的异步异常,保证系统稳定。自定义异步任务的调度行为(比如微任务、Timer)。 什么是 Zone࿱…...

HarmonyOS学习——ArkTS语法介绍之基本知识
ArkTS是一种为构建高性能应用而设计的编程语言。ArkTS在继承TypeScript语法的基础上进行了优化,以提供更高的性能和开发效率。 目前流行的编程语言TypeScript是在JavaScript基础上通过添加类型定义扩展而来的,而ArkTS则是TypeScript的进一步扩展。TypeS…...

电子电器架构 --- 网关转发时延解析
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 钝感力的“钝”,不是木讷、迟钝,而是直面困境的韧劲和耐力,是面对外界噪音的通透淡然。 生活中有两种人,一种人格外在意别人的眼光;另一种人无论…...
)
minio数据迁移(两台服务器没法相互通信)
场景描述: A服务器 无法访问 B服务器,B服务器 也无法访问 A(即双方都不能通过公网或内网直连对方) MinIO 官方提供了 mc(MinIO Client)命令行工具,可以直接实现 Bucket 之间的数据迁移: 安装 …...

笔记,麦克风的灵敏度
麦克风的“灵敏度(Sensitivity)”决定了它捕捉声音细节的能力。想象麦克风是一只有耳朵的生物。高灵敏度麦克风像长着“超级顺风耳”的精灵,能听见花瓣飘落的声音、远处树叶的沙沙声,甚至你心跳的微弱震动。适合录音棚里捕捉歌手的…...

特殊配合力(SCA)作为全基因组关联分析(GWAS)的表型,其生物学意义和应用价值
生物学意义 解析非加性遗传效应 特殊配合力(SCA)主要反映特定亲本组合的杂交优势,由非加性遗传效应(如显性、超显性、上位性)驱动。显性效应涉及等位基因间的显性互作,上位性效应则涉及不同位点间的基因互作。通过SCA-GWAS,可以定位调控这些非加性效应的关键基因组区域…...

2025年 全新 AI 编程工具 Cursor 安装使用教程
一、Cursor 软件下载 首选,登录Cursor官网,进行软件下载,官网下载地址如下: Cursor AI IDE 下载 二、Cursor软件安装配置 此处以Windows10系统安装为例,下载完成之后,右键安装包,以管理员身份…...

HarmonyOS 鸿蒙操作物联网设备蓝牙模块、扫描蓝牙、连接蓝牙和蓝牙通信
01【HarmonyOS 蓝牙】 物联网无线传输方案、HarmonyOS蓝牙数据通信之前的准备工作 02【HarmonyOS 蓝牙】配置蓝牙权限 检测 打开 关闭蓝牙 扫描蓝牙 显示蓝牙设备 03【HarmonyOS 蓝牙】连接蓝牙 发现服务 获取特征值 读取信息 写入信息 和蓝牙模块交互 04【物联网 Wifi模块…...

MVC是什么?分别对应SpringBoot哪些层?
作为Java开发者,理解MVC在SpringBoot中的实现方式直接影响我们构建可维护的Web应用能力。本文将用生产级代码示例揭示各层对应关系,并分享分层设计中的实用技巧。 一、MVC本质:解耦的艺术(SpringBoot视角) 1. 经典MVC三元组 组件职责SpringBoot对应层典型代码注解Model数…...

【质量管理】TRIZ因果链分析:解码质量问题的“多米诺效应“
为什么要使用因果链分析 没有发现问题并不等于没有问题。爱因斯坦曾说,如果我只有一个小时的时间来拯救世界,我将花45分钟时间分析问题,10分钟的时间来检查问题,最后5分钟的时间来解决问题。可见问题分析的重要性。 在质量管理实践…...

解决librechat 前端界面没有google gemini 2.5模型的选项
问题概述 根据librechat 的更新清单,是支持了google gemini的模型,但是却找不到界面上较新的 2.5模型的配置选项。 通过查阅项目的文档(GitHub), 看到: 由于目前还不支持获取模型列表,因此您应…...

STM32实现simpleFOC控制无刷电机
一、FOC基础知识学习 使用simpleFOC控制无刷电机前,需要大概了解一下相关知识,包括力矩控制、速度控制、位置控制的原理和它们之间的联系。 推荐学习资料: 教你写一个比SimpleFOC更好的电机库_哔哩哔哩_bilibili 《灯哥手把手教你写FOC算…...

Redis-数据一致性问题与解决方案
Redis-数据一致性问题与解决方案 引言 Redis 是一个高性能的内存数据库,广泛应用于缓存、会话存储、实时分析等场景。作为一个 NoSQL 数据库,它的高性能和丰富的数据结构使其成为现代微服务架构中不可或缺的组件。然而,在高并发的环境下&am…...
