扩增子分析|微生物生态网络稳定性评估之鲁棒性（Robustness）和易损性（Vulnerability）在R中实现

一、引言

       周集中老师团队于2021年在Nature climate change发表的文章，阐述了网络稳定性评估的原理算法，并提供了完整的代码。自此对微生物生态网络的评估具有更全面的指标，自此网络稳定性的评估广受大家欢迎。本系列将介绍网络稳定性之鲁棒性和易损性指数的原理，计算方法以及代码，如有疑问欢迎讨论交流。

       为了理解增温是否以及如何影响构建的微生物生态网络（MEN）的稳定性，我们使用了多种指标来表征网络及其嵌入成员的稳定性，包括稳健性、易损性、节点和连接的稳定性、节点持久性以及组成稳定性。我们通过消除模拟和经验观察评估了网络及网络内微生物群落的稳定性。这一节集中于基于模拟的方式评估网络稳定性的稳健性（Robustness）和易损性指标。下一节我们将讨论基于经验观测值评估网络稳定性。

二、基础知识之基于模拟的网络稳定性

稳健性（Robustness）

       微生物生态网络（MEN）的稳健性定义为在随机或定向移除节点后网络中剩余物种的比例。在随机移除物种的模拟中，随机移除一定比例的节点；在定向移除模拟中，移除了一定数量的模块中心节点。为了测试物种移除对剩余物种的影响，计算了节点 i 的加权平均相互作用强度（wMIS），其公式如下：

       式中，bj是物种 j 的相对丰度；

                 sij 是物种 i 和 j 之间的关联强度，以皮尔森相关系数表示。因此在本研究中，sij = sji。

         从MEN中移除选定节点后，如果 wMISi = 0（即所有与物种 i 的链接均被移除）或 wMISi< 0（即物种 i 与其他物种之间的共生协同不足以维持其生存），则节点 i 被视为灭绝/孤立并从网络中移除。该过程持续进行，直到所有物种的 wMIS 均为正数。剩余节点的比例即为网络的稳健性。在随机移除50%的节点或移除5个模块枢纽节点的情况下，测量了网络的稳健性。

图中a，稳健性测量方法是从每个经验MEN 中随机移除 50% 的分类单元后剩余的分类单元比例。b，稳健性测量方法是从每个经验MEN中移除五个模块中心后剩余的分类单元比例。在a和b中，每个误差线对应于 100 次模拟的标准差。变暖（W）和控制（Ctl）之间的显著性差异（双侧t检验）用 *** P < 0.001表示。

易损性（Vulnerability）

       每个节点的易损性衡量该节点对全局效率的相对贡献。网络的易损性由网络中节点的最大易损性表示，公式如下：

       式中，E 是网络的全局效率;

                 Ei 是移除节点 i 及其所有链接后的全局效率。

       网络图的全局效率计算为所有节点对间效率的平均值：

       式中，d(i, j) 表示节点 i 和节点 j 之间最短路径上的边数量。

       效率描述了信息在网络中传播的速度。在生态网络中，效率可以提供关于生物或生态事件后果在网络局部或整体传播速度的信息。

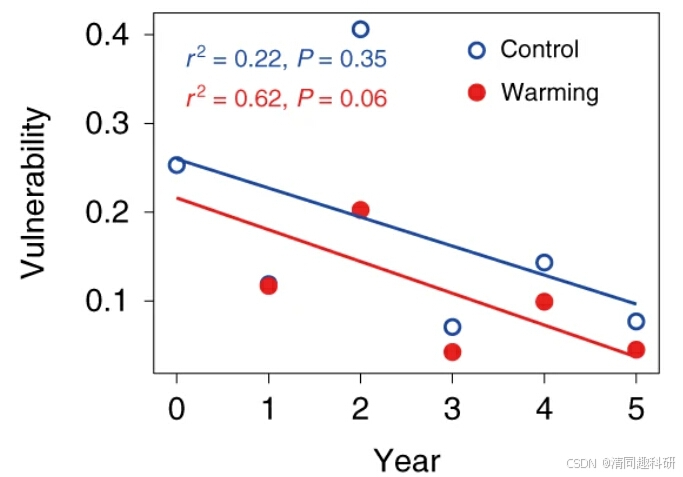
图中，网络易损性通过每个网络中的最大节点易损性来衡量。显示了线性回归的调整后R2和P值。

三、示例数据及R代码

      本文的示例数据和代码均来自于2021年周集中老师团队的Nature climate change文章，感兴趣的同学可以自行去学习。

3.1 鲁棒性（Robustness）指标

🌟准备数据

准备otu.csv表格，该表格为要计算鲁棒性的网络otu数据表。代码每次计算一个网络的稳健性，因此需要计算几个网络就运行几次代码，每次将输入文件名修改。

🌟完整代码

# 清理工作环境中的所有对象
rm(list = ls())
# 读取 OTU 表格数据
otutab <- read.csv("control_otu.csv", row.names = 1)
otutab[is.na(otutab)] <- 0  # 将 NA 值替换为 0
# 筛选出在至少 12 个样本中存在的 OTU
counts <- rowSums(otutab > 0)
otutab <- otutab[counts >= 12,]
# 转置 OTU 表，计算每种物种的相对丰度
comm <- t(otutab)
sp.ra <- colMeans(comm) / 30000  # 每种物种的相对丰度
#从 OTU 表中计算相关矩阵
cormatrix <- matrix(0, ncol(comm), ncol(comm))  # 初始化相关矩阵
for (i in 1:ncol(comm)) {for (j in i:ncol(comm)) {speciesi <- sapply(1:nrow(comm), function(k) {ifelse(comm[k, i] > 0, comm[k, i], ifelse(comm[k, j] > 0, 0.01, NA))})speciesj <- sapply(1:nrow(comm), function(k) {ifelse(comm[k, j] > 0, comm[k, j], ifelse(comm[k, i] > 0, 0.01, NA))})corij <- cor(log(speciesi)[!is.na(speciesi)], log(speciesj)[!is.na(speciesj)])  # 计算对数变换后的相关性cormatrix[i, j] <- cormatrix[j, i] <- corij  # 填充对称矩阵}
}# 设置行名和列名为物种名称
row.names(cormatrix) <- colnames(cormatrix) <- colnames(comm)# 仅保留相关系数大于等于 0.80 的连接
cormatrix2 <- cormatrix * (abs(cormatrix) >= 0.80)
cormatrix2[is.na(cormatrix2)] <- 0  # 将 NA 替换为 0
diag(cormatrix2) <- 0  # 去除自连接# 计算网络连接数量和节点数量
sum(abs(cormatrix2) > 0) / 2  # 连接数
sum(colSums(abs(cormatrix2)) > 0)  # 至少有一个连接的节点数# 提取连接网络的矩阵
network.raw <- cormatrix2[colSums(abs(cormatrix2)) > 0, colSums(abs(cormatrix2)) > 0]
sp.ra2 <- sp.ra[colSums(abs(cormatrix2)) > 0]
sum(row.names(network.raw) == names(sp.ra2))  # 检查是否匹配# 鲁棒性模拟函数
# 随机移除部分物种后计算剩余物种比例
rand.remov.once <- function(netRaw, rm.percent, sp.ra, abundance.weighted = TRUE) {id.rm <- sample(1:nrow(netRaw), round(nrow(netRaw) * rm.percent))net.Raw <- netRawnet.Raw[id.rm, ] <- 0;  net.Raw[, id.rm] <- 0  # 移除物种if (abundance.weighted) {net.stength <- net.Raw * sp.ra} else {net.stength <- net.Raw}sp.meanInteration <- colMeans(net.stength)id.rm2 <- which(sp.meanInteration <= 0)  # 移除无连接的物种remain.percent <- (nrow(netRaw) - length(id.rm2)) / nrow(netRaw)remain.percent
}# 鲁棒性模拟
rmsimu <- function(netRaw, rm.p.list, sp.ra, abundance.weighted = TRUE, nperm = 100) {t(sapply(rm.p.list, function(x) {remains <- sapply(1:nperm, function(i) {rand.remov.once(netRaw = netRaw, rm.percent = x, sp.ra = sp.ra, abundance.weighted = abundance.weighted)})remain.mean <- mean(remains)remain.sd <- sd(remains)remain.se <- sd(remains) / sqrt(nperm)result <- c(remain.mean, remain.sd, remain.se)names(result) <- c("remain.mean", "remain.sd", "remain.se")result}))
}# 加权和非加权模拟
Weighted.simu <- rmsimu(netRaw = network.raw, rm.p.list = seq(0.05, 1, by = 0.05), sp.ra = sp.ra2, abundance.weighted = TRUE, nperm = 100)
Unweighted.simu <- rmsimu(netRaw = network.raw, rm.p.list = seq(0.05, 1, by = 0.05), sp.ra = sp.ra2, abundance.weighted = FALSE, nperm = 100)# 整合结果
dat1 <- data.frame(Proportion.removed = rep(seq(0.05, 1, by = 0.05), 2),rbind(Weighted.simu, Unweighted.simu),weighted = rep(c("weighted", "unweighted"), each = 20),year = rep(2014, 40),treat = rep("Warmed", 40)#根据自己的处理修改treat名称
)# 保存结果到文件
write.csv(dat1, "random_removal_result_Y14_W.csv")# 加载 ggplot2 包
library(ggplot2)# 生成加权网络的结果图
ggplot(dat1[dat1$weighted == "weighted",], aes(x = Proportion.removed, y = remain.mean, group = treat, color = treat)) +geom_line() +geom_pointrange(aes(ymin = remain.mean - remain.sd, ymax = remain.mean + remain.sd), size = 0.2) +scale_color_manual(values = c("blue", "red")) +xlab("Proportion of species removed") +ylab("Proportion of species remained") +theme_light() +facet_wrap(~year, ncol = 3)# 生成非加权网络的结果图
ggplot(dat1[dat1$weighted == "unweighted",], aes(x = Proportion.removed, y = remain.mean, group = treat, color = treat)) +geom_line() +geom_pointrange(aes(ymin = remain.mean - remain.sd, ymax = remain.mean + remain.sd), size = 0.2) +scale_color_manual(values = c("blue", "red")) +xlab("Proportion of species removed") +ylab("Proportion of species remained") +theme_light() +facet_wrap(~year, ncol = 3)

🌟输出结果

如下所示，结果输出名为random_removal_result_Y14_W.csv的表格。

在随机移除50%的节点情况下即Proportion.removed值为0.5时，获得该网络的鲁棒性值0.21278；标准差是0.01966，该值对应于 100 次模拟的标准差。

⚠️ weighted考虑到物种丰度了，ubweighted没有考虑物种丰度。

随后可基于这个结果绘制柱状图或其他图纸。

⚠️移除5个模块中心点的鲁棒性值计算代码我们也放在了示例代码和数据文件中，需要的可以留言获取。

3.2 易损性（vulnerability）指标

🌟准备数据

准备otu.csv表格，该表格为要计算易损性的网络otu数据表。

代码每次计算一个网络的易损性，因此需要计算几个网络就运行几次代码，每次将输入文件名修改。

🌟完整代码

# 清理工作环境中的所有对象
rm(list = ls())# 导入igraph包和自定义的centrality函数
if(!require("igraph")){install.packages("igraph")}
library(igraph)
source("info.centrality.R")#自定义函数#### 获取图结构（Graph）####
# 可以通过以下三种方式获取图结构：
# 1. 读取已有的图
# 2. 从OTU表中构建图
# 3. 从MENAP下载的相关矩阵构建图## 2) 从OTU表中构建图
# 读取OTU表，缺失值替换为0
otutab <- read.csv("treat_otu.csv",  row.names = 1)
otutab[is.na(otutab)] <- 0# 筛选至少出现在12个样本中的OTU
counts <- rowSums(otutab > 0)
otutab <- otutab[counts >= 12,]# 转置OTU表，以便进行后续计算
comm <- t(otutab)# 初始化相关矩阵，存储物种间的相关性
cormatrix <- matrix(0, ncol(comm), ncol(comm))# 使用嵌套循环计算OTU之间的相关性
for (i in 1:ncol(comm)) {for (j in i:ncol(comm)) {speciesi <- sapply(1:nrow(comm), function(k) {ifelse(comm[k, i] > 0, comm[k, i], ifelse(comm[k, j] > 0, 0.01, NA))})speciesj <- sapply(1:nrow(comm), function(k) {ifelse(comm[k, j] > 0, comm[k, j], ifelse(comm[k, i] > 0, 0.01, NA))})# 计算物种对数值的相关性corij <- cor(log(speciesi)[!is.na(speciesi)], log(speciesj)[!is.na(speciesj)])cormatrix[i, j] <- cormatrix[j, i] <- corij}
}# 设置相关矩阵的行名和列名
row.names(cormatrix) <- colnames(cormatrix) <- colnames(comm)# 仅保留相关系数大于等于0.80的连接
cormatrix2 <- cormatrix * (abs(cormatrix) >= 0.80)
cormatrix2[is.na(cormatrix2)] <- 0
diag(cormatrix2) <- 0  # 移除自连接
cormatrix2[abs(cormatrix2) > 0] <- 1  # 转换为邻接矩阵# 从邻接矩阵构建无向图g
g <- graph_from_adjacency_matrix(as.matrix(cormatrix2), mode = "undirected", weighted = NULL, diag = FALSE)### 结束图构建部分# 移除孤立节点
iso_node_id <- which(degree(g) == 0)
g2 <- delete.vertices(g, iso_node_id)  # 生成不含孤立节点的图g2# 检查节点和连接数
length(V(g2))  # 节点数
length(E(g2))  # 边数# 计算每个节点的易损性
node.vul <- info.centrality.vertex(g2)
max(node.vul)  # 输出最大易损性

🌟输出结果

四、参考文献

[1] Yuan, M.M., Guo, X., Wu, L. et al. Climate warming enhances microbial network complexity and stability. Nat. Clim. Chang. 11, 343–348 (2021).

[2] Mengting-Maggie-Yuan/warming-network-complexity-stability

五、相关信息

！！！本文内容由小编总结互联网和文献内容总结整理，如若侵权，联系立即删除！

 ！！！有需要的小伙伴评论区获取今天的测试代码和实例数据。

 📌示例代码中提供了数据和代码，小编已经测试，可直接运行。

以上就是本节所有内容。