如何用数学思想填报高考志愿
人一辈子有很多四年,但是很少有哪个四年对你一生的影响能超过大学这四年。
从18岁到22岁的这几年,是一个人真正成年的过程,很多人会在这段时间里认识一生的朋友,谈第一次真正的恋爱,第一次离开父母,自己生活,第一次醉酒,第一次挣钱……所以,填志愿这件事的重要性,要远远超出学什么、将来做什么工作这个有限的目标。
大学填报志愿比你找一个合适的对象求婚还需要谨慎,结婚了还可以离婚,你选错了大学基本没办法后悔,而且这个标签会跟你一辈子。
本质上,填报高考志愿是数学上的最优化求解问题。你须知道自己的边界条件,然后在有限的方程里求解。应用的说方法是:你优化的目标是什么呢?是未来的总收入?是你找到如意伴侣的概率?是你父母的幸福指数?更糟糕的是,如果你把高考成绩这个变量加进来,那这个问题就更复杂了。对于不同的成绩,相对应的优化的函数和最优解是完全不同的。
所以,应该这么说,具体问题具体分析,在不知道这个孩子具体情况的时候,就没办法回答这个问题了。你对自己的认知越清晰,也就是边界条件越规范,那么你的解的合理性就最优。
给定任何一个学生的高考成绩,这三个维度的优化往往是存在矛盾的。比如,你的成绩可以让你在一所名校上一个冷门的烂专业,或者在一个差一些的学校上一个热门、抢手的专业。再比如,两所学校让你挑,A校排名好,但是在三线城市,B校排名靠后,但是在一线城市,你该怎么选呢?一个人在本科就早早计划好了将来干什么,未必是件好事,太功利、太算计,反倒会让你失去更好的可能性。更好的策略是在一所优秀的大学学好英语、数学之类的基础,然后等毕业的时候,决定研究生去学什么跟职业有关的技能。
填志愿的优化问题用数学思想可以被分解成三个维度来考虑:
一、学校的“好坏”;
二、学校所在的城市的“好坏”;
三、学科的“好坏”。
绝对有益的建议:
第一,学校的好坏比学科的好坏重要。
一个案例是瓦西里老师,他是北京大学国际政治系毕业的。可能你不知道,瓦西里老师多年前就是一家国际著名广告公司中国创意总监,后来成立了自己的公司,是一个非常成功的广告业牛人。这一切都跟他大学的专业无关,但是跟他大学时代的经历、朋友、环境有不可分割的关系。这么说吧,如果当年瓦西里老师选择去一个二流学校学颇为时髦的广告专业,那他现在说不定还在什么写字楼里辛勤地思考文案呢。
第二,学校所在城市很重要。
简单地说,就是选择到有活力、机会多的城市去上大学。有活力的大城市给你提供的不只是更多的实习、就业机会,人、环境、经历这些对于你会产生更长远的影响因素也许更加重要。在一个小地方上大学,你除了在校园里闷着无处可去,说不定还会养成打游戏的恶习,而在北京混四年,你不知道你会碰到什么有趣的牛人。北上杭广属于绝对的一线城市,机会多多。成都、南京、西安等城市的文化底蕴和生活舒适度度绝对是冠绝天下的,自己要有一定的了解。
所以,综上所述,合乎数学思想的思考的顺序如下:
首先,不考虑专业,按照你的高考成绩,把能上的学校按照从好到坏排序。找出排在前面的N个“985工程”学校,如果N=0,那么建议重考或放弃高考。第二步,从第一所大学开始,看大学所在城市。 如果这所大学是“中国科技大学”,那么跳到第三步。如果所在城市是一线城市,那么报这所大学,跳到第三步。如果不是,那么接着看下一所。如果到最后还没有出现一线城市,那么建议重考或者放弃高考。第三步,在已选定的学校里,把所有专业按照“录取分高低”排序,找出自己考分能上的最高选项。
相关文章:

如何用数学思想填报高考志愿
人一辈子有很多四年,但是很少有哪个四年对你一生的影响能超过大学这四年。 从18岁到22岁的这几年,是一个人真正成年的过程,很多人会在这段时间里认识一生的朋友,谈第一次真正的恋爱,第一次离开父母,自己生…...
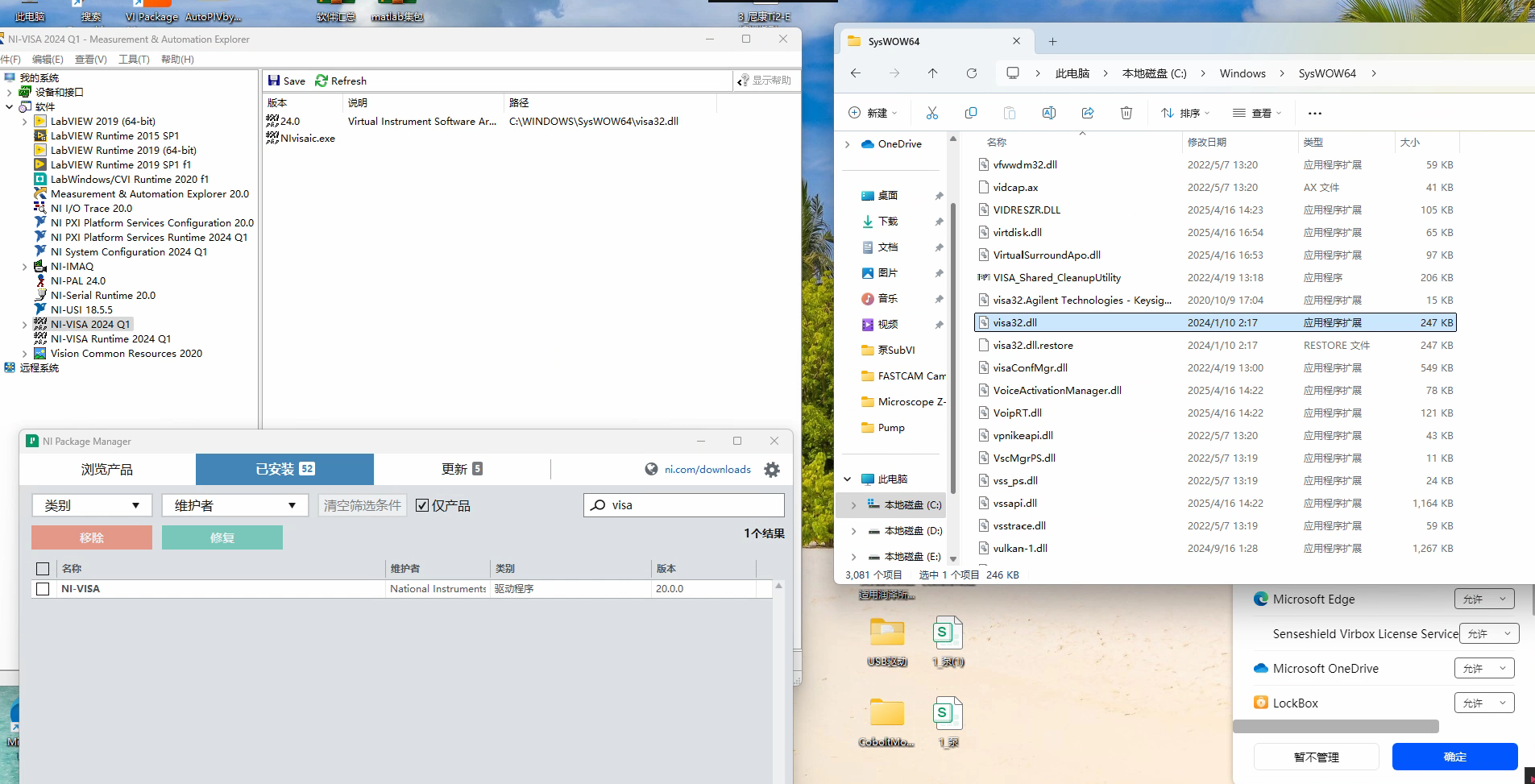
LabVIEW 2019 与 NI VISA 20.0 安装及报错处理
在使用 Windows 11 操作系统的电脑上,同时安装了 LabVIEW 2019 32 位和 64 位版本的软件。此前安装的 NI VISA 2024 Q1 版,该版本与 LabVIEW 2019 32 位和 64 位不兼容,之后重新安装了 NI VISA 20.0。从说明书来看,NI VISA 20.0 …...

探索 JWT(JSON Web Token):原理、结构与实践应用对比
目录 前言1. 什么是 JWT?2. JWT 的组成结构详解2.1 Header(头部)2.2 Payload(负载)2.3 Signature(签名) 3. JWT 的实际作用3.1 身份认证3.2 信息传递与授权 4. JWT 与 Cookie、API Key 的比较4.…...

互联网大厂Java求职面试:云原生与AI融合下的系统设计挑战-1
互联网大厂Java求职面试:云原生与AI融合下的系统设计挑战-1 在当今云计算和人工智能迅猛发展的背景下,互联网大厂对Java工程师的要求已从传统的单体架构和业务逻辑处理,转向了更复杂的云原生架构设计、AI模型集成以及高并发系统的性能优化能…...

【Redis进阶】持久化
一、MySQL事务特性及Redis持久化需求 (一)MySQL事务特性 MySQL的事务具有四大核心特性,这些特性对于保证数据库操作的准确性和可靠性至关重要。 原子性:事务中的所有操作要么全部成功,要么全部失败…...

[docker基础一]docker简介
目录 一 消除恐惧 1) 什么是虚拟化,容器化 2)案例 3)为什么需要虚拟化,容器化 二 虚拟化实现方式 1)应用程序执行环境分层 2)虚拟化常见类别 3)常见虚拟化实现 一)主机虚拟化(虚拟机)实现 二)容器虚拟化实现 一 消除恐…...

Texify - 数学公式OCR转换工具
文章目录 一、项目概览相关资源核心特性 二、安装指南三、使用示例1、命令行转换2、Python API调用3、交互式应用 四、性能基准运行你自己的基准测试 五、局限性 一、项目概览 Texify 是一个OCR模型,可将包含数学公式的图片或PDF转换为Markdown和LaTeX格式…...

RISC-V CLINT、PLIC及芯来ECLIC中断机制分析 —— RISC-V中断机制(一)
在长期的嵌入式开发实践中,对中断机制的理解始终停留在表面层次,特别当开发者长期局限于纯软件抽象层面时,对中断机制的理解极易陷入"知其然而不知其所以然"的困境,这种认知的局限更为明显;随着工作需要不断…...

时钟晶振锁相环pll方向技术要点和大厂题目解析
本专栏预计更新60期左右。当前第9期。 本专栏不仅适用于硬件的笔试面试,同样也适用于梳理硬件核心的知识点。 通过本文能得到什么? 首先,根据实战经验总结时钟晶振,锁相环的主要知识点,技术要点,面试考点; 然后,列出时钟晶振,锁相环的笔试面试的主要题型真题和模拟题,…...

图像处理篇--- HTTP|RTSP|MJPEG视频流格式
文章目录 前言一、MJPEG (Motion JPEG)基本概念技术特点编码方式传输协议数据格式 优势实现简单低延迟兼容性好容错性强 劣势带宽效率低不支持音频缺乏标准控制 典型应用 二、RTSP (Real Time Streaming Protocol)基本概念技术特点协议栈工作流程传输模式 优势专业流媒体支持高…...

【Harbor v2.13.0 详细安装步骤 安装证书启用 HTTPS】
Harbor v2.13.0 详细安装步骤(启用 HTTPS) 1. 环境准备 系统要求:至少 4GB 内存,100GB 磁盘空间。 已安装组件: Docker(版本 ≥ 20.10)Docker Compose(版本 ≥ v2.0) 域…...

C++中的static_cast:类型转换的安全卫士
C中的static_cast:类型转换的安全卫士 在C编程中,类型转换是不可避免的操作,而static_cast作为C四大强制类型转换运算符之一,是最常用且相对安全的一种转换方式。今天我们就来深入探讨一下这个重要的类型转换工具。 一、static_…...

开源与商业:图形化编程工具的博弈与共生
一、开源生态的破局之路:从技术实验到行业标准 在 2025 年全球开发者生态大会上,iVX 凭借 “全栈代码生成 AI 驱动开发” 的技术架构,被行业权威机构评选为 “年度技术创新典范”。作为 2012 年启动的开源项目,iVX 历经 17 年技…...

Docker + Watchtower 实现容器自动更新:高效运维的终极方案
文章目录 前言一、Watchtower 简介二、Watchtower 安装与基本使用1. 快速安装 Watchtower2. 监控特定容器 三、Watchtower 高级配置1. 设置检查间隔2. 配置更新策略3. 清理旧镜像4. 通知设置 四、生产环境最佳实践1. 使用标签控制更新2. 更新前执行健康检查3. 结合CI/CD流水线 …...

(二)Linux下基本指令 2
【知识预告】 16. date 指令 17. cal 指令 18. find 指令 19. which指令 20. whereis 指令 21. alias 指令 22. grep 指令 23. zip/unzip 指令 24. tar 指令 25. bc 指令 26. uname ‒r 指令 27. 重要的⼏个热键 28. 关机 16 date 指令 指定格式显⽰时间:date %Y-…...

1 2 3 4 5顺序插入,形成一个红黑树
红黑树的特性与优点 红黑树是一种自平衡的二叉搜索树,通过额外的颜色标记和平衡性约束,确保树的高度始终保持在 O(log n)。其核心特性如下: 每个节点要么是红色,要么是黑色。根节点和叶子节点(NIL节点)是…...

无线网络设备中AP和AC是什么?有什么区别?
无线网络设备中AP和AC是什么?有什么区别? 一. 什么是AP?二. 什么是AC?三. AP与AC的关系 前言 肝文不易,点个免费的赞和关注,有错误的地方请指出,看个人主页有惊喜。 作者:神的孩子都…...

Web自动化测试入门详解
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 一、目的 web自动化测试作为软件自动化测试领域中绕不过去的一个“香饽饽”,通常都会作为广大测试从业者的首选学习对象,相较于C/S架…...

WHAT - 简单服务发现
文章目录 简单理解举个例子简单服务发现方式1. 静态配置(最简单,但不灵活)2. DNS 发现3. 使用服务注册中心(稍高级) 总结 “简单服务发现”(Simple Service Discovery)通常指的是一种让系统中的…...

uniapp+vue3+firstUI时间轴 提现进度样式
展示 说明:“status”: 0, //状态:0待审核,1审核通过,2审核驳回,3提现成功,4提现失败 第一种:5种类型归纳为三种显示样式 <fui-timeaxis background"#fff" :padding"[10rpx,16rpx,0]"><!-- 动态生成步骤节点 --><f…...

【日撸 Java 三百行】Day 10(综合任务 1)
目录 Day 10:综合任务 1 一、题目分析 1. 数据结构 2. 相关函数基本知识 二、模块介绍 1. 初始化与成绩矩阵的构建 2. 创建总成绩数组 3. 寻找成绩极值 三、代码与测试 小结 拓展:关于求极值的相关算法 Day 10:综合任务 1 Task&…...

VR 南锣鼓巷:古老街区的数字化绘卷与沉浸式遨游
VR 技术,即虚拟现实技术,是一种能够创建和体验虚拟世界的计算机仿真系统。它利用计算机生成一种模拟环境,通过多源信息融合的交互式三维动态视景和实体行为的系统仿真,使用户沉浸到该环境中,产生身临其境的感受 。简单…...

使用Java NIO 实现一个socket通信框架
使用Java NIO(非阻塞I/O)实现一个Socket通信框架,可以让你构建高性能的网络应用。NIO提供了Channel、Buffer和Selector等核心组件,支持非阻塞模式下的网络编程。下面是一个简单的例子,展示了如何使用Java NIO创建一个基本的服务器端和客户端进行Socket通信。 1.服务器端 …...

Android开发-常用布局
在Android应用开发中,布局决定了用户界面的结构和元素之间的相对位置。选择合适的布局不仅能够提升用户体验,还能提高代码的可维护性和灵活性。本文将介绍几种最常用的Android布局方式,包括LinearLayout、RelativeLayout、ConstraintLayout以…...

macOS 15.4.1 Chrome不能访问本地网络
前言 最近使用macmini m4,自带macOS15系统,对于开发者简直是一言难尽,Chrome浏览器的本地网络有bug,可以访问本机,但是不能访问路由器上的其他机器,路由器提供的页面也不能访问,如下是折腾解决…...

【Hive入门】Hive增量数据导入:基于Sqoop的关系型数据库同步方案深度解析
目录 引言 1 增量数据导入概述 1.1 增量同步与全量同步对比 1.2 增量同步技术选型矩阵 2 Sqoop增量导入原理剖析 2.1 Sqoop架构设计 2.2 增量同步核心机制 3 Sqoop增量模式详解 3.1 append模式(基于自增ID) 3.2 lastmodified模式(基…...

Dify使用总结
最近完成了一个Dify的项目简单进行总结下搭建服务按照官方文档操作就行就不写了。 进入首页之后由以下组成: 探索、工作室、知识库、工具 探索: 可以展示自己创建的所有应用,一个应用就是一个APP,可以进行测试使用 工作室包含…...

MATLAB导出和导入Excel文件表格数据并处理
20250507 1.MATLAB使用table函数和writetable函数将数据导出Excel表格文件 我们以高斯函数为例子,高斯函数在数学和工程领域有着广泛的应用,它的一般形式为: 其中是均值,决定了函数的中心位置; 是标准差,决…...

分书问题的递归枚举算法
分数问题的递归枚举算法 一、问题引入二、解题步骤1.问题分析思维导图2.解题步骤 三、代码实现1.代码2.复杂度分析 四、个人总结 一、问题引入 分书问题是指:已知 n 个人对 m 本书的喜好(n≤m),现要将 m 本书分给 n 个人…...

Unity WebGL、js发布交互
官网参考 Unity3D开发之WebGL平台上 unity和js前端通信交互 WebFun.jslib mergeInto(LibraryManager.library, {JSLog: function (str) { var strsUTF8ToString(str); Log(str); Log(strs);}, Hello: function () {var strs"Hello, world!"; Log(strs); Log(UTF8ToS…...
