【高数上册笔记篇02】:数列与函数极限
【参考资料】
- 同济大学《高等数学》教材
- 樊顺厚老师B站《高等数学精讲》系列课程 (注:本笔记为个人数学复习资料,旨在通过系统化整理替代厚重教材,便于随时查阅与巩固知识要点)
仅用于个人数学复习,因为课本太厚了而且不方便带着,所以才整理这样一份笔记。
文章目录
- 一、数列的极限
- 1.1 无穷的本质:你先说
- 1.2 极限的严格定义
- 1.3 一个简单题
- 二、收敛数列的性质
- 2.1 极限唯一性
- 2.2 收敛数列有界性
- 2.3 收敛数列的保号性
- 2.4 收敛数列和子数列
- 2.4 两个推论(省略证明)
- 三、函数极限
一、数列的极限
1.1 无穷的本质:你先说
我们先来看几个具体的数列例子:
-
数列: 1 2 , 2 3 , 3 4 , … , n n + 1 , … \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \ldots, \frac{n}{n+1}, \ldots 21,32,43,…,n+1n,… 通项公式为: x n = n n + 1 x_n = \frac{n}{n+1} xn=n+1n
-
数列: 2 , 4 , 8 , … , 2 n , … 2, 4, 8, \ldots, 2^n, \ldots 2,4,8,…,2n,… 通项公式为: x n = 2 n x_n = 2^n xn=2n
-
数列: 1 , − 1 , 1 , … , ( − 1 ) n + 1 , … 1, -1, 1, \ldots, (-1)^{n+1}, \ldots 1,−1,1,…,(−1)n+1,… 通项公式为: x n = ( − 1 ) n + 1 x_n = (-1)^{n+1} xn=(−1)n+1
对于任意给定的正数 M > 0 M > 0 M>0(你先给个 M M M),总存在某个时刻 N N N,使得当 n > N n > N n>N 时,对应的数列项 x n x_n xn 满足: x n > M x_n > M xn>M
{ n n + 1 } \left\{\frac{n}{n+1}\right\} {n+1n} 当 n → ∞ n \to \infty n→∞ 时, n n + 1 \frac{n}{n+1} n+1n 无限接近于 1 1 1。
1.2 极限的严格定义
为了更精确地描述“无限接近”的概念,我们需要引入极限的严格定义。对于任意给定的正数 ε > 0 \varepsilon > 0 ε>0(无论这个 ε \varepsilon ε 多么小),总存在一个正整数 N N N,使得当 n > N n > N n>N 时,以下不等式成立:
∣ n n + 1 − 1 ∣ < ε \left|\frac{n}{n+1} - 1\right| < \varepsilon n+1n−1 <ε
换句话说,对于任意小的正数 ε \varepsilon ε,我们总能找到一个时刻 N N N,使得当 n > N n > N n>N 时,数列项 n n + 1 \frac{n}{n+1} n+1n 与 1 1 1 的差的绝对值小于 ε \varepsilon ε。
Def: 设 { x n } \{x_n\} {xn} 是一个数列。如果存在一个常数 a a a,使得对任给的 ε > 0 \varepsilon > 0 ε>0,存在一个 N N N,当 n > N n > N n>N 时,不等式
∣ x n − a ∣ < ε |x_n - a| < \varepsilon ∣xn−a∣<ε
都成立,则称 a a a 为数列 { x n } \{x_n\} {xn} 的极限,记作:
lim n → ∞ x n = a \lim_{n \to \infty}{x_n} = a n→∞limxn=a
如果 { x n x_n xn} 极限存在,也称为 { x n x_n xn} 收敛,否则是发散。等价关系如下:
lim n → ∞ x n = a ⟺ { ∀ ε > 0 , ∃ N > 0 , 使得当 n > N 时 , ∣ x n − a ∣ < ε \lim_{n \to \infty} x_n = a \iff \begin{cases} \forall \varepsilon > 0, \\ \exists N > 0, \\ \text{使得当 } n > N \text{ 时}, \\ |x_n - a| < \varepsilon \end{cases} n→∞limxn=a⟺⎩ ⎨ ⎧∀ε>0,∃N>0,使得当 n>N 时,∣xn−a∣<ε
几何意义:
对于任意给定的正数 ε > 0 \varepsilon > 0 ε>0,如果存在一个正整数 N N N,使得当 n > N n > N n>N 时,以下不等式成立:
∣ x n − a ∣ < ε |x_n - a| < \varepsilon ∣xn−a∣<ε
这可以进一步展开为:
− ε < x n − a < ε -\varepsilon < x_n - a < \varepsilon −ε<xn−a<ε
从而得到:
a − ε < x n < a + ε a - \varepsilon < x_n < a + \varepsilon a−ε<xn<a+ε
这意味着当 n > N n > N n>N 时,数列项 x n x_n xn 都位于区间 ( a − ε , a + ε ) (a - \varepsilon, a + \varepsilon) (a−ε,a+ε) 内,即:
x n ∈ U ( a , ε ) x_n \in U(a, \varepsilon) xn∈U(a,ε)
其中 U ( a , ε ) U(a, \varepsilon) U(a,ε) 表示以 a a a 为中心、半径为 ε \varepsilon ε 的邻域。
即: N N N 项之后,每一项都落在邻域 U ( a , ε ) U(a, \varepsilon) U(a,ε) 内,只有有限项落在 U ( a , ε ) U(a, \varepsilon) U(a,ε) 外。
1.3 一个简单题
lim n → ∞ n n + 1 = 1 \lim_{{n \to \infty}} \frac{n}{n+1} = 1 n→∞limn+1n=1
证明:
对任意给定的 ε > 0 \varepsilon > 0 ε>0,存在一个正整数 N N N,使得当 n > N n > N n>N 时,有:
∣ n n + 1 − 1 ∣ < ε \left|\frac{n}{n+1} - 1\right| < \varepsilon n+1n−1 <ε
因为 1 n + 1 < 1 n \frac{1}{n+1} < \frac{1}{n} n+11<n1, 所以只要 1 n < ε \frac{1}{n} < {\varepsilon} n1<ε,即 n > 1 ε n > \frac{1}{\varepsilon} n>ε1
那么,取 N = [ 1 ε ] + 1 N = \left[\frac{1}{\varepsilon}\right] + 1 N=[ε1]+1,当 n > N n > N n>N 时,有:
∣ n n + 1 − 1 ∣ = 1 n + 1 < 1 n < ε \left|\frac{n}{n+1} - 1\right| = \frac{1}{n+1} < \frac{1}{n} < \varepsilon n+1n−1 =n+11<n1<ε
∴ lim n → ∞ n n + 1 = 1 ∴ \lim_{{n \to \infty}} \frac{n}{n+1} = 1 ∴n→∞limn+1n=1
二、收敛数列的性质
2.1 极限唯一性
Th1(极限的唯一性):数列的极限存在,必唯一。
证:(用反证法)
假设 lim n → ∞ x n = a \lim_{{n \to \infty}} x_n = a limn→∞xn=a, lim n → ∞ x n = b \lim_{{n \to \infty}} x_n = b limn→∞xn=b,且 a < b a < b a<b。
由数列极限的定义,对 ε = b − a 3 \varepsilon = \frac{b - a}{3} ε=3b−a,则 ∃ N 1 > 0 \exists N_1 > 0 ∃N1>0,当 n > N 1 n > N_1 n>N1 时,
∣ x n − a ∣ < b − a 3 (1) |x_n - a| < \frac{b - a}{3} \quad \text{(1)} ∣xn−a∣<3b−a(1)
又 ∃ N 2 > 0 \exists N_2 > 0 ∃N2>0,当 n > N 2 n > N_2 n>N2 时,
∣ x n − b ∣ < b − a 3 (2) |x_n - b| < \frac{b - a}{3} \quad \text{(2)} ∣xn−b∣<3b−a(2)
取 N = max ( N 1 , N 2 ) N = \max(N_1, N_2) N=max(N1,N2),当 n > N n > N n>N 时,同时满足不等式(1)和(2)。
b − a = ∣ ( x n − a ) − ( x n − b ) ∣ ≤ ∣ x n − a ∣ + ∣ x n − b ∣ < b − a 3 + b − a 3 = 2 3 ( b − a ) 矛盾! b - a = \left| (x_n - a) - (x_n - b) \right| \\[1em] \leq |x_n - a| + |x_n - b| \\[1em] < \frac{b - a}{3} + \frac{b - a}{3} = \frac{2}{3}(b - a) \\[1em] 矛盾! b−a=∣(xn−a)−(xn−b)∣≤∣xn−a∣+∣xn−b∣<3b−a+3b−a=32(b−a)矛盾!
2.2 收敛数列有界性
若存在正数 M > 0 M>0 M>0 ,使得 ∣ x n ∣ ≤ M |x_n| \leq M ∣xn∣≤M对一切 n n n 成立,则称数列 { x n } \{x_n\} {xn}为有界数列。
Th2:收敛数列必有界。(但是有界不一定收敛,如sinx)
证: 设 { x n } \{x_n\} {xn}为收敛数列
lim n → ∞ x n = a \lim_{{n \to \infty}} x_n = a n→∞limxn=a
由极限的定义.:对于 ε = 1 \varepsilon=1 ε=1,存在 N > 0 N>0 N>0, ∀ n > N \forall n>N ∀n>N时, ∣ x n − a ∣ < 1 |x_n - a| < 1 ∣xn−a∣<1
∣ x n ∣ = ∣ ( x n − a ) + a ∣ ≤ ∣ x n − a ∣ + ∣ a ∣ < 1 + ∣ a ∣ |x_n| = |(x_n - a) + a| \\[1em] \leq |x_n - a| + |a| < 1 + |a| ∣xn∣=∣(xn−a)+a∣≤∣xn−a∣+∣a∣<1+∣a∣
取 M = max { ∣ x 1 ∣ , ∣ x 2 ∣ , … , ∣ x N ∣ , 1 + ∣ a ∣ } M = \max\{|x_1|, |x_2|, \ldots, |x_N|, 1 + |a|\} M=max{∣x1∣,∣x2∣,…,∣xN∣,1+∣a∣},则对一切 n n n,有:
∣ x n ∣ ≤ M ∴ { x n } 为有界数列 |x_n| \leq M \\[1em] \therefore \{x_n\} 为有界数列 ∣xn∣≤M∴{xn}为有界数列
2.3 收敛数列的保号性
如果 lim n → ∞ x n = a \lim_{{n \to \infty}} x_n = a limn→∞xn=a存在且 a > 0 a > 0 a>0,则存在正整数 N > 0 N > 0 N>0,当 n > N n > N n>N时,都有 x n > 0 x_n > 0 xn>0。如果 a < 0 a<0 a<0,同理。
证: 由于 lim n → ∞ x n = a \lim_{{n \to \infty}} x_n = a limn→∞xn=a,若 a > 0 a > 0 a>0
由定义 对 ε = a 2 \varepsilon = \frac{a}{2} ε=2a,存在 N > 0 N > 0 N>0,当 n > N n > N n>N时
∣ x n − a ∣ < a 2 |x_n - a| < \frac{a}{2} ∣xn−a∣<2a
− a 2 < x n − a < a 2 -\frac{a}{2} < x_n - a < \frac{a}{2} −2a<xn−a<2a
此时: ( n > N ) (n > N) (n>N)
x n > a − a 2 = a 2 > 0 证毕! x_n > a - \frac{a}{2} = \frac{a}{2} > 0 \\[1em] 证毕! xn>a−2a=2a>0证毕!
2.4 收敛数列和子数列
Th4:如果数列 { x n } \{x_n\} {xn}收敛于 a a a,则它的任一子数列也收敛且收敛于 a a a。
证: 由于 lim n → ∞ x n = a \lim_{{n \to \infty}} x_n = a limn→∞xn=a,∴ 对任意给定的 ε > 0 \varepsilon > 0 ε>0,存在 N N N,当 n > N n > N n>N时。
∣ x n − a ∣ < ε |x_n - a| < \varepsilon ∣xn−a∣<ε
取 K = N K = N K=N,当 k > K k > K k>K时:
n k > n K ≥ N ∣ x n k − a ∣ < ε ∴ lim k → ∞ x n k = a n_k > n_K \geq N \\[1em] |x_{n_k} - a| < \varepsilon \\[1em] \therefore \lim_{{k \to \infty}} x_{n_k} = a nk>nK≥N∣xnk−a∣<ε∴k→∞limxnk=a
一个简单题:
要证明数列 lim n → ∞ ( − 1 ) n + 1 \lim_{n \to \infty} (-1)^{n+1} limn→∞(−1)n+1 不存在,我们可以利用子数列的性质。根据子数列定理,如果一个数列收敛于某个极限 a a a,那么它的任意子数列也收敛于同一个极限 a a a。
我们考虑数列 { x n } = ( − 1 ) n + 1 \{x_n\} = (-1)^{n+1} {xn}=(−1)n+1 的两个子数列:
-
子数列 { x 2 k − 1 } \{x_{2k-1}\} {x2k−1},即所有奇数项组成的子数列:
x 2 k − 1 = ( − 1 ) ( 2 k − 1 ) + 1 = ( − 1 ) 2 k = 1 x_{2k-1} = (-1)^{(2k-1)+1} = (-1)^{2k} = 1 x2k−1=(−1)(2k−1)+1=(−1)2k=1
因此,这个子数列是常数序列 1,显然有:
lim k → ∞ x 2 k − 1 = 1 \lim_{k \to \infty} x_{2k-1} = 1 k→∞limx2k−1=1 -
子数列 { x 2 k } \{x_{2k}\} {x2k},即所有偶数项组成的子数列:
x 2 k = ( − 1 ) 2 k + 1 = − 1 x_{2k} = (-1)^{2k+1} = -1 x2k=(−1)2k+1=−1
因此,这个子数列是常数序列 -1,显然有:
lim k → ∞ x 2 k = − 1 \lim_{k \to \infty} x_{2k} = -1 k→∞limx2k=−1
由于这两个子数列分别收敛于不同的极限值 1 和 -1,根据子数列定理,原数列 { x n } = ( − 1 ) n + 1 \{x_n\} = (-1)^{n+1} {xn}=(−1)n+1 不能收敛于任何一个确定的极限值。因此,可以得出结论:
lim n → ∞ ( − 1 ) n + 1 不存在 \lim_{n \to \infty} (-1)^{n+1} \text{ 不存在} n→∞lim(−1)n+1 不存在
2.4 两个推论(省略证明)
-
推论1:如果数列 { x n x_n xn} 从某一项起, x n ≥ 0 x_n ≥ 0 xn≥0 ( x n ≤ 0 x_n ≤ 0 xn≤0), lim n → ∞ x n = a \lim_{{n \to \infty}} x_n = a limn→∞xn=a,则 a ≥ 0 a ≥ 0 a≥0 ( a ≤ 0 a ≤ 0 a≤0)
-
推论2:设 lim n → ∞ a n = a \lim_{{n \to \infty}} a_n = a limn→∞an=a, lim n → ∞ b n = b \lim_{{n \to \infty}} b_n = b limn→∞bn=b,若 a < b a < b a<b,则存在正整数 N > 0 N > 0 N>0,使 n > N n > N n>N时 b n > a n b_n > a_n bn>an
三、函数极限
对任意给定的 ε > 0 \varepsilon > 0 ε>0,存在 X > 0 X > 0 X>0,当 x > X x > X x>X 时,都有 ∣ f ( x ) − A ∣ < ε |f(x) - A| < \varepsilon ∣f(x)−A∣<ε,则称 A A A 是 f ( x ) f(x) f(x) 当 x → ∞ x \to \infty x→∞ 的极限。
几何意义: y = A y=A y=A 是 y = f ( x ) y=f(x) y=f(x) 图形的水平渐近线。
求下式子:
f ( x ) = x 2 − 1 x − 1 f(x) = \frac{x^2 - 1}{x - 1} f(x)=x−1x2−1
当 x ≠ 1 x \neq 1 x=1:
f ( x ) = x 2 − 1 x − 1 = ( x − 1 ) ( x + 1 ) x − 1 f(x) = \frac{x^2 - 1}{x - 1} = \frac{(x - 1)(x + 1)}{x - 1} f(x)=x−1x2−1=x−1(x−1)(x+1)
f ( x ) = x + 1 f(x) = x + 1 f(x)=x+1
所以,当 x ≠ 1 x \neq 1 x=1 时,
f ( x ) = x + 1 f(x) = x + 1 f(x)=x+1
当 x = 1 x=1 x=1 时:
对任意给定的 ε > 0 \varepsilon > 0 ε>0,要找到一个 δ > 0 \delta > 0 δ>0,使得当 0 < ∣ x − 1 ∣ < δ 0 < |x - 1| < \delta 0<∣x−1∣<δ 时,
∣ x 2 − 1 x − 1 − 2 ∣ < ε \left|\frac{x^2 - 1}{x - 1} - 2\right| < \varepsilon x−1x2−1−2 <ε
由于 f ( x ) = x + 1 f(x) = x + 1 f(x)=x+1 当 x ≠ 1 x \neq 1 x=1,因此:
∣ x + 1 − 2 ∣ = ∣ x − 1 ∣ |x + 1 - 2| = |x - 1| ∣x+1−2∣=∣x−1∣
所以,只要取 δ = ε \delta = \varepsilon δ=ε,当 0 < ∣ x − 1 ∣ < δ 0 < |x - 1| < \delta 0<∣x−1∣<δ 时,就有:
∣ x − 1 ∣ < ε |x - 1| < \varepsilon ∣x−1∣<ε
这表明对任意 ε > 0 \varepsilon > 0 ε>0,确实存在 δ = ε > 0 \delta = \varepsilon > 0 δ=ε>0,使得当 0 < ∣ x − 1 ∣ < δ 0 < |x - 1| < \delta 0<∣x−1∣<δ 时,有:
∣ x 2 − 1 x − 1 − 2 ∣ < ε \left|\frac{x^2 - 1}{x - 1} - 2\right| < \varepsilon x−1x2−1−2 <ε
因此, lim x → 1 x 2 − 1 x − 1 = 2 \lim_{x \to 1} \frac{x^2 - 1}{x - 1} = 2 limx→1x−1x2−1=2。
注: 定义中 0 < ∣ x − x 0 ∣ 0 < |x - x_0| 0<∣x−x0∣表示 x ≠ x 0 x \neq x_0 x=x0,讨论 x → x 0 x \to x_0 x→x0时只考虑 x ≠ x 0 x \neq x_0 x=x0,且 lim x → x 0 f ( x ) \lim_{x \to x_0} f(x) limx→x0f(x)是否存在与 f ( x 0 ) f(x_0) f(x0)是否有定义无关。
lim x → x 0 f ( x ) = A ⟺ { ∀ ε > 0 ∃ δ > 0 当 0 < ∣ x − x 0 ∣ < δ 时 ∣ f ( x ) − A ∣ < ε \lim_{x \to x_0} f(x) = A \iff \begin{cases} \forall \varepsilon > 0 \\ \exists \delta > 0 \\ \text{当 } 0 < |x - x_0| < \delta \text{ 时} \\ |f(x) - A| < \varepsilon \end{cases} x→x0limf(x)=A⟺⎩ ⎨ ⎧∀ε>0∃δ>0当 0<∣x−x0∣<δ 时∣f(x)−A∣<ε

相关文章:

【高数上册笔记篇02】:数列与函数极限
【参考资料】 同济大学《高等数学》教材樊顺厚老师B站《高等数学精讲》系列课程 (注:本笔记为个人数学复习资料,旨在通过系统化整理替代厚重教材,便于随时查阅与巩固知识要点) 仅用于个人数学复习,因为课…...

c++STL-string的模拟实现
cSTL-string的模拟实现 string的模拟实现string的模拟线性表的实现构造函数析构函数获取长度(size)和获取容量(capacity)访问 [] 和c_str迭代器(iterator)交换swap拷贝构造函数赋值重载(&#x…...

YashanDB(崖山数据库)V23.4 LTS 正式发布
2024年回顾 2024年11月我们受邀去深圳参与了2024国产数据库创新生态大会。在大会上崖山官方发布了23.3。这个也是和Oracle一样采用的事编年体命名。 那次大会官方希望我们这些在一直从事在一线的KOL帮助产品提一些改进建议。对于这样的想法,我们都是非常乐于合作…...

python 写一个工作 简单 番茄钟
1、图 2、需求 番茄钟(Pomodoro Technique)是一种时间管理方法,由弗朗西斯科西里洛(Francesco Cirillo)在 20 世纪 80 年代创立。“Pomodoro”在意大利语中意为“番茄”,这个名字来源于西里洛最初使用的一个…...

C++.IP协议通信
C++IP协议通信 1. TCP协议通信1.1 服务端实现创建套接字绑定地址监听连接接受连接数据传输关闭连接1.2 客户端实现创建套接字连接服务器数据传输关闭连接1.3 示例代码服务端代码示例客户端代码示例绑定地址接收数据发送数据关闭套接字2.2 客户端实现创建套接字发送数据接收数据…...

css背景相关
背景书写 background: url(src); // 注意:在写动态样式时,backgournd赋值格式错误,是不会在浏览器dom的style上显示的 // 但是可以创建不可见的img,预加载来提高性能背景也会加载图片资源 同img的src一样,background也…...

PyCharm 加载不了 conda 虚拟环境,不存在的
#工作记录 前言 在开发过程中,PyCharm 无法加载 Conda 虚拟环境是常见问题。 在不同情况下,“Conda 可执行文件路径”的指定可能会发生变化,不会一尘不变,需要灵活处置。 以下是一系列解决此问题的经验参考。 检查 Conda 安装…...
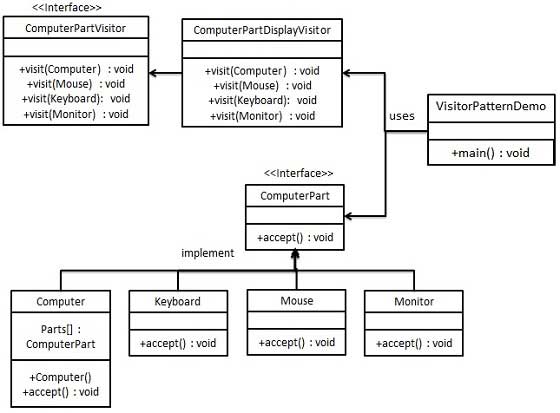
设计模式学习整理
目录 UML类图 设计模式六大原则 1.单一职责原则 2.里氏替换原则 3.依赖倒置原则 4.接口隔离原则 5.迪米特法则(最少知道原则) 6.开(放封)闭原则 设计模式分类 1.创建型模式 2.结构型模式 4.行为型模式 一、工厂模式(factory——简单工厂模式和抽象工厂模式) 1.1、…...

二分查找的理解
#define _CRT_SECURE_NO_WARNINGS #include <stdio.h>int binary_search(int arr[], int k, int sz) {int left 0;int right sz - 1;//这个是下标,减一是因为在0开始的,怕越界(访问无效)while (left < right){int mid…...

【Java】线程实例化 线程状态 线程属性
线程实例化 继承 Thread 类 创建类继承自 Thread 类 . class MyThread extends Thread重写 run() 方法 . Overridepublic void run(){// 线程要执行的任务代码}实例化自定义线程类 . 实现 Runnable 接口 创建类实现 Runnable 接口 . class MyRunnable implements Runnable实…...

卫宁健康WiNGPT3.0与WiNEX Copilot 2.2:医疗AI创新的双轮驱动分析
引言:医疗AI的双翼时代 在医疗信息化的浪潮中,人工智能技术的深度融入正在重塑整个医疗行业。卫宁健康作为国内医疗健康和卫生领域数字化解决方案的领军企业,持续探索AI技术在医疗场景中的创新应用。2025年5月10日,在第29届中国医院信息网络大会(CHIMA2025)上,卫宁健康…...

I2C通讯
3.1. 本章节的代码仓库 1 2 3 4 5 6 #如之前有获取则可跳过 #获取仓库 git clone https://gitee.com/LubanCat/lubancat_rk_code_storage.git#代码所在的位置 lubancat_rk_code_storage/quick_start/i2c3.2. i2c I2C(Inter-Integrated Circuit)是一种通用的总线协…...

Excel实现单元格内容拼接
一、应用场景: 场景A:将多个单元格拼接,比如写测试用例时,将多个模块拼接,中间用“-”隔开 场景B:将某单元格内容插入另一单元格固定位置(例如在B1中添加A1的内容) 二、实际应用&a…...

2025前端面试遇到的问题(vue+uniapp+js+css)
Vue相关面试题 vue2和vue3的区别 一、核心架构差异 特性Vue2Vue3响应式系统基于Object.defineProperty基于Proxy(支持动态新增/删除属性)代码组织方式Options API(data/methods分块)Composition API(逻辑按功能聚合&am…...

大模型核心基础简介
大模型核心基础简介目录 一、大模型简介定义核心特征 二、大模型的发展历程1. 早期奠基(1950s–2010s)1950s–1980s:神经网络萌芽1990s–2010s:深度学习前夜 2. 架构革命:Transformer的诞生与预训练范式(20…...

广东省省考备考(第八天5.11)—言语:逻辑填空(每日一练)
错题 解析 第一空,搭配“期盼”,且根据“生命,是来自上天的馈赠”,可知父母对孩子的出生是非常期盼的。A项“望穿秋水”,形容对远地亲友的殷切盼望,C项“望眼欲穿”,形容盼望殷切,均…...

github+ Picgo+typora
github Picgotypora 本文将介绍如何使用Picgo在typora中实现上传服务 创建github仓库以及配置token 创建仓库 注意需要Initialize 添加README 配置为public 配置token github点击头像找到setting 选择Developer setting 配置token generate 选第一个第二个都行(我这里选第…...
[网安工具] IP 信息收集工具 —— LBD · 使用手册
🌟想了解其它网安工具?看看这个:[网安工具] 网络安全工具管理 —— 工具仓库 管理手册 lbd | Kali Linux ToolsVideolbd Usage ExampleTest to see if the target domain (example.com) is using a load balancer:rootkali:~# lbd example.c…...

本贴会成为记录贴
这几天有些心力交瘁了 一方面带着对互联网下行的伤心,一方面是对未来的担忧 一转眼好像就是20 21那个 可以在宿舍肆意玩手机 大学生活 可是我不小了 是个26岁的人了 时间很快 快的就好像和自己开了一个玩笑 我以为可以找到一个自己足够喜欢的 可爱的人 可是我没有 …...

说说es配置项的动态静态之分和集群配置更新API
这天因为某件工作来到了es官网某个参数配置相关的页面,注意到了下图圆圈里的“Dynamic”: 链接:https://www.elastic.co/guide/en/elasticsearch/reference/8.1/modules-cluster.html#misc-cluster-settings 显然这是对配置项的一个描述&am…...

LLMs之Mistral Medium 3:Mistral Medium 3的简介、安装和使用方法、案例应用之详细攻略
LLMs之Mistral Medium 3:Mistral Medium 3的简介、安装和使用方法、案例应用之详细攻略 目录 Mistral Medium 3 简介 1、Mistral Medium 3 特点 Mistral Medium 3 安装和使用方法 2、使用方法 (1)、创建Agent (2)、模型微调 Mistral Medium 3 案例应用 Mistr…...

并发设计模式实战系列(17):信号量(Semaphore)
🌟 大家好,我是摘星! 🌟 今天为大家带来的是并发设计模式实战系列,第十七章信号量(Semaphore),废话不多说直接开始~ 目录 一、核心原理深度拆解 1. 信号量本质模型 2. 并发控制…...

RAGMCP基本原理说明和相关问题解惑
一、RAG架构原理和局限性 1.1 概念解释 RAG(Retrieval-Augmented Generation):检索增强生成,让大模型接受外部输入后,总结输出 向量数据库:向量数据通常是高维空间中的点,代表复杂的数据结构…...

Java学习手册:服务注册与发现
一、服务注册与发现的概念 在微服务架构中,服务注册与发现是核心功能之一。由于微服务架构中服务实例的数量和位置是动态变化的,服务注册与发现机制允许服务实例在启动时自动注册到注册中心,并在停止时自动注销。其他服务可以通过查询注册中…...
双向Transformer:BERT(Bidirectional Encoder Representations from Transformers)
基于Transformer架构,通过双向上下文建模训练,提高完成任务的性能。 一 BERT的核心理念 1.1双向上下文建模依赖 之前讲的双向递归是用两个RNN进行,而BERT是通过Transformer的自注意力机制同时捕捉上下文信息。 1.1.1掩码语言模型…...

EdgeOne Pages MCP 入门教程
什么是MCP? MCP (Model Context Protocol) 是一个开放协议,允许 AI 模型安全地与本地和远程资源进行交互。通过在支持 MCP 的客户端(如 Cline、Cursor、Claude 等)上进行统一配置,可以让 AI 访问更多资源并使用更多工…...

Maven 公司内部私服中央仓库搭建 局域网仓库 资源共享 依赖包构建共享
介绍 公司内部私服搭建通常是为了更好地管理公司内部的依赖包和构建过程,避免直接使用外部 Maven 中央仓库。通过搭建私服,团队能够控制依赖的版本、提高构建速度并增强安全性。公司开发的一些公共工具库更换的提供给内部使用。 私服是一种特殊的远程仓…...

1688代采系统:技术架构与应用实践
在电商领域,1688 作为国内领先的 B2B 电商平台,拥有海量的商品信息。这些数据对于企业采购决策、市场分析、价格监控和供应链管理具有重要价值。本文将详细介绍如何使用 Python 爬虫技术,通过 1688 的商品详情接口(item_search 和…...

一种混沌驱动的后门攻击检测指标
摘要 人工智能(AI)模型在各个领域的进步和应用已经改变了我们与技术互动的方式。然而,必须认识到,虽然人工智能模型带来了显著的进步,但它们也存在固有的挑战,例如容易受到对抗性攻击。目前的工作提出了一…...

【2025最新】为什么用ElasticSearch?和传统数据库MySQL与什么区别?
Elasticsearch 深度解析:从原理到实践 一、为什么选择 Elasticsearch? 数据模型 Elasticsearch 是基于文档的搜索引擎,它使用 JSON 文档来存储数据。在 Elasticsearch 中,相关的数据通常存储在同一个文档中,而不是分散…...
