蓝桥杯14届 数三角
问题描述
小明在二维坐标系中放置了 n 个点,他想在其中选出一个包含三个点的子集,这三个点能组成三角形。然而这样的方案太多了,他决定只选择那些可以组成等腰三角形的方案。请帮他计算出一共有多少种选法可以组成等腰三角形?
输入格式
输入共 n+1 行。
第一行为一个正整数 n。
后面 n 行,每行两个整数 xi, yi 表示第 i 个点的坐标。
输出格式
输出共 1 行,一个整数。
样例输入
5
1 1
4 1
1 0
2 1
1 2
样例输出
4
样例说明
一共有 4 种选法: {3,4,5}、{1,3,4}、{5,2,3}、{1,4,5}。
评测用例规模与约定
对于 20% 的数据,保证 n≤200。
对于 100% 的数据,保证 n≤2000,0≤xi,yi≤。
因为每个点横纵坐标都是整数不会出现等边三角形这种情况
枚举每一个点作为顶点,所有与该顶点距离相等的点均位于以该顶点为圆心、以该距离为半径的圆周上
观察所有与该顶点距离相等的点是否有对称点,除去三点共线的情况,并且这一条线会被记录两次,所以在答案我们要去掉cnt/2
解释 ans += mp[d]; :
与顶点距离相同的点有2个点时,能构成1个等腰三角形
与顶点距离相同的点有3个点时,能构成3个等腰三角形 (+2)
与顶点距离相同的点有4个点时,能构成6个等腰三角形(+3)
与顶点距离相同的点有5个点时,能构成10个等腰三角形(+4)
求一个点在圆上关于圆心的对称点:

#include<iostream>
#include<set> // 包含 set
#include<map> // 包含 map
using namespace std;const int N = 2e3+10;
int n;
int ans;
int x[N], y[N];set<pair<int, int>>s; //存储所有点的坐标
map<int, int>mp;//计算i, j两点间距离的平方
//使用平方距离避免浮点数运算
int dis(int i, int j)
{return (x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]);
}int main()
{cin>>n;for(int i=1; i<=n; ++i){cin>>x[i]>>y[i];s.insert({x[i], y[i]});}//枚举每个点作为等腰三角形的顶点for(int i=1; i<=n; ++i){int cnt=0; //记录共线三点的情况出现的次数//对于每个顶点i,遍历所有其他点jfor(int j=1; j<=n; ++j){//确保不把顶点自己和自己比较if(i!=j){int d=dis(i, j);ans += mp[d]; //之前已经有mp[d]个点到 i 的距离也是 dmp[d]++; //更新该距离的点数//检查共线情况int x2=2*x[i]-x[j]; //计算对称点x坐标int y2=2*y[i]-y[j]; //计算对称点y坐标 if(s.count({x2,y2}))cnt++; //如果对称点存在,则三点共线}}ans-=cnt/2; //每对对称点会被统计两次mp.clear(); //清空mp,准备下一个顶点的统计}cout<<ans;return 0;
}相关文章:

蓝桥杯14届 数三角
问题描述 小明在二维坐标系中放置了 n 个点,他想在其中选出一个包含三个点的子集,这三个点能组成三角形。然而这样的方案太多了,他决定只选择那些可以组成等腰三角形的方案。请帮他计算出一共有多少种选法可以组成等腰三角形? 输…...

redis sentinel和redis cluster的主从切换选举过程
引言 redis sentinel和redis cluster的主从切换选举过程不同,本文将从选举机制、核心差异对比两者的不同。 一、Redis Sentinel的选举机制 监控与故障判定 Sentinel集群通过心跳检测(每秒一次PING)监控主节点状态: 主观下线&…...

C++自学笔记 makefile
本博客参考南科大于仕琪教授的讲解视频和这位同学的学习笔记: 参考博客 感谢两位的分享。 makefile 的作用 用于组织大型项目的编译,是一个一键编译项目的脚本文件。 本博客通过四个版本的makefile逐步说明makefile的使用 使用说明 四个演示文件 …...

前端密码加密:保护用户数据的第一道防线
引言 在当今互联网时代,用户数据安全至关重要,而密码作为用户身份验证的核心凭证,其安全性更是重中之重。传统的前端开发中,密码常常以明文形式传输到服务器,这带来了严重的安全隐患。本文将深入探讨前端密码加密的必…...

HTML12:文本框和单选框
表单元素格式 属性说明type指定元素的类型。text、password、 checkbox、 radio、submit、reset、file、hidden、image 和button,默认为textname指定表单元素的名称value元素的初始值。type为radio时必须指定一个值size指定表单元素的初始宽度。当type为text 或pas…...

机器人厨师上岗!AI在餐饮界掀起新风潮!
想要了解人工智能在其他各个领域的应用,可以查看下面一篇文章 《AI在各领域的应用》 餐饮业是与我们日常生活息息相关的行业,而人工智能(AI)正在迅速改变这个传统行业的面貌。从智能点餐到食材管理,再到个性化推荐&a…...

MySQL开篇
文章目录 一、前置知识1. MySQL的安装2. 前置一些概念知识 二、MySQL数据库操作2.1 概念2.2 数据库的操作2.2.1创建数据库命令2.2.2 查看数据库2.2.3 选中数据库2.2.4 删除数据库 三、MySQL数据表操作3.1 概念3.2 数据表的操作3.2.1 创建表 一、前置知识 1. MySQL的安装 MySQ…...

Linux电脑本机使用小皮面板集成环境开发调试WEB项目
开发调试WEB项目,有时开发环境配置繁琐,可以使用小皮面板集成环境。 小皮面板官网: https://www.xp.cn/1.可以使用小皮面板安装脚本一键安装。登陆小皮面板管理后台 2.在“软件商店”使用LNMP一键部署集成环境。 3.添加网站,本…...

问题及解决01-面板无法随着窗口的放大而放大
在MATLAB的App Designer中,默认情况下,组件的位置是固定的,不会随着父容器的大小变化而改变。问题图如下图所示。 解决: 为了让Panel面板能够随着UIFigure父容器一起缩放,需要使用布局管理器,我利用 MATLA…...

操作系统原理实验报告
操作系统原理课程的实验报告汇总 实验三:线程的创建与撤销 实验环境:计算机一台,内装有VC、office等软件 实验日期:2024.4.11 实验要求: 1.理解:Windows系统调用的基本概念,进程与线程的基…...

《Linux命令行大全(第2版)》PDF下载
内容简介 本书对Linux命令行进行详细的介绍,全书内容包括4个部分,第一部分由Shell的介绍开启命令行基础知识的学习之旅;第二部分讲述配置文件的编辑,如何通过命令行控制计算机;第三部分探讨常见的任务与必备工具&…...

Java高频面试之并发编程-15
hello啊,各位观众姥爷们!!!本baby今天又来报道了!哈哈哈哈哈嗝🐶 面试官:as-if-serial 是什么?单线程的程序一定是顺序执行的吗? as-if-serial 规则 定义: …...

Python-86:奇妙货币交易问题
问题描述 小R住在一个名为 X 国的国家,这里的货币非常特殊,面值为 V0,V1,V2,...,VnV0,V1,V2,...,Vn,并且 nn 可以无限大。该国的交易规则也很特别:在一次交易中,双方只能对每种面值的货币使用不超过两次。 例如&…...

Selenium的driver.get_url 和 手动输入网址, 并点击的操作,有什么不同?
我在搞爬取的时候,发现有些网站直接用driver.get(url) 跳转到目标特定的网址的时候,会被强制跳转到其他的网址上,但是如果是自己手动,在网址栏那里输入网址,并点回车,却能完成跳转。 这是在使用 Selenium …...

kotlin @JvmStatic注解的作用和使用场景
1. JvmStatic 的作用 JvmStatic 是 Kotlin 提供的一个注解,用于在 JVM 上将伴生对象(companion object)中的方法或属性暴露为 Java 静态方法或字段。 作用对象:只能用在 companion object 中的函数或属性。效果: 在 …...

GitHub中多个PR时,如何协同合并和管理
在 GitHub 中,当多个开发者同时提交多个 Pull Request(PR)时,合理的管理流程与协作策略能够确保代码库稳定、审查高效,并减少冲突与重工。总体而言,你需要: 1)统一分支与命名策略&a…...

无人甘蔗小车履带式底盘行走系统的研究
1.1 研究背景与意义 1.1.1 研究背景 甘蔗作为全球最重要的糖料作物之一,在农业经济领域占据着举足轻重的地位。我国是甘蔗的主要种植国家,尤其是广西、广东、云南等地,甘蔗种植面积广泛,是当地农业经济的重要支柱产业。甘蔗不仅…...

通俗易懂版知识点:Keepalived + LVS + Web + NFS 高可用集群到底是干什么的?
实验开始前,先搞懂为什么要部署该集群? 这个方案的目标是让网站 永不宕机,即使某台服务器挂了,用户也感觉不到。它主要涉及 负载均衡(LVS) 高可用(Keepalived) 共享存储ÿ…...

各类有关NBA数据统计数据集大合集
这些数据我已上传大家在CSDN上直接搜索就可以! 一、【2022-2023 NBA球员统计】数据集 关键词: 篮球 描述: 语境 该数据集每场比赛包含2022-2023常规赛NBA球员统计数据。 请注意,由团队更改产生了重复的球员名称。 * [2021-2022 NBA播放器统计]&#…...

《社交应用架构生存战:React Native与Flutter的部署容灾决胜法则》
React Native和Flutter作为当下热门的跨平台开发框架,在社交应用开发领域各显神通。今天,我们深入探索它们在高可用架构中的部署与容灾策略。 React Native凭借其独特优势,在社交应用开发中拥有一席之地。它基于JavaScript和React࿰…...
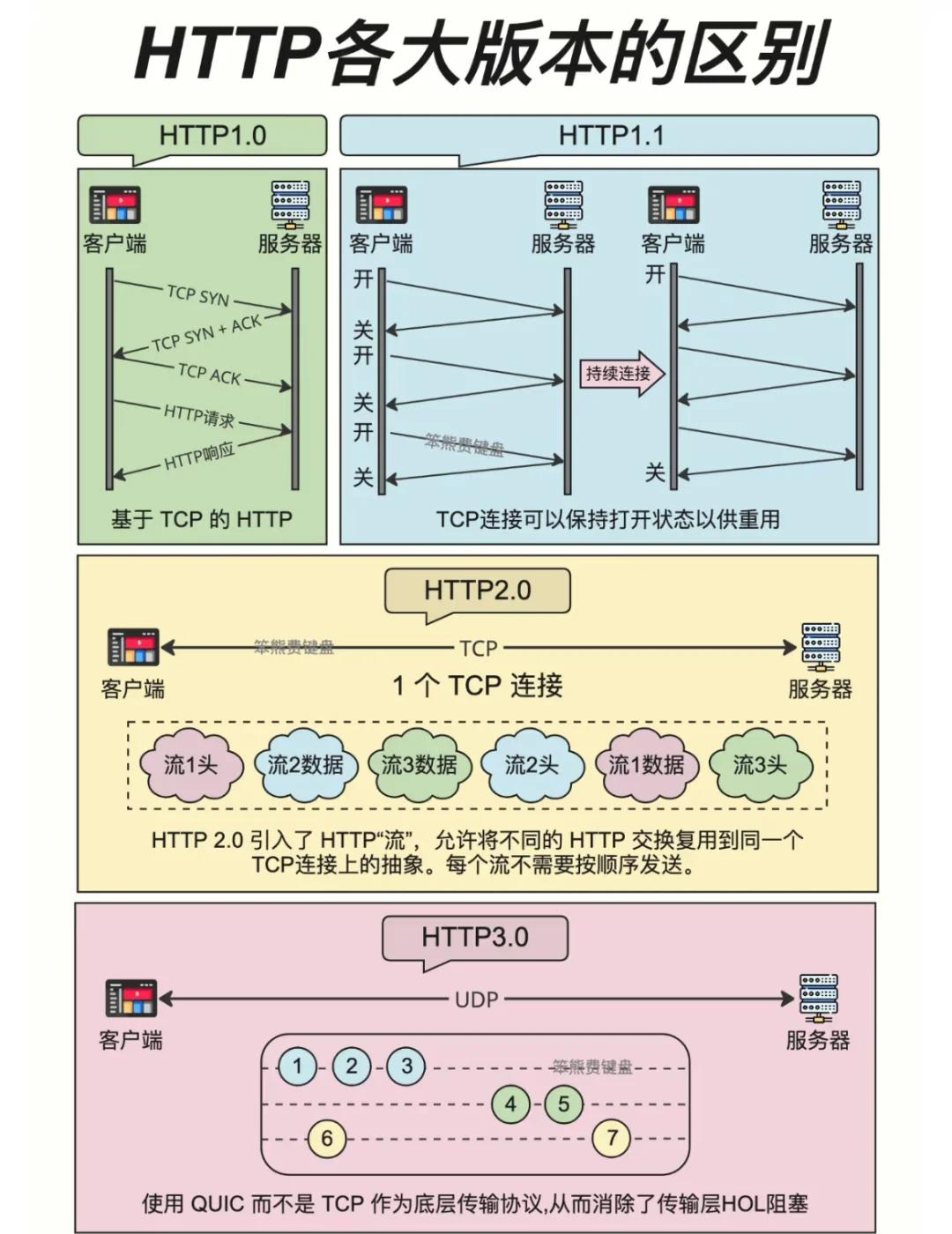
https,http1,http2,http3的一些知识
温故知新,突然有人问我项目中🤔有使用http3么,一下不知从何说起,就有了这篇文章的出现。 https加密传输,ssltls https 验证身份 提供加密,混合加密 : 对称加密 非对称加密 原理:…...
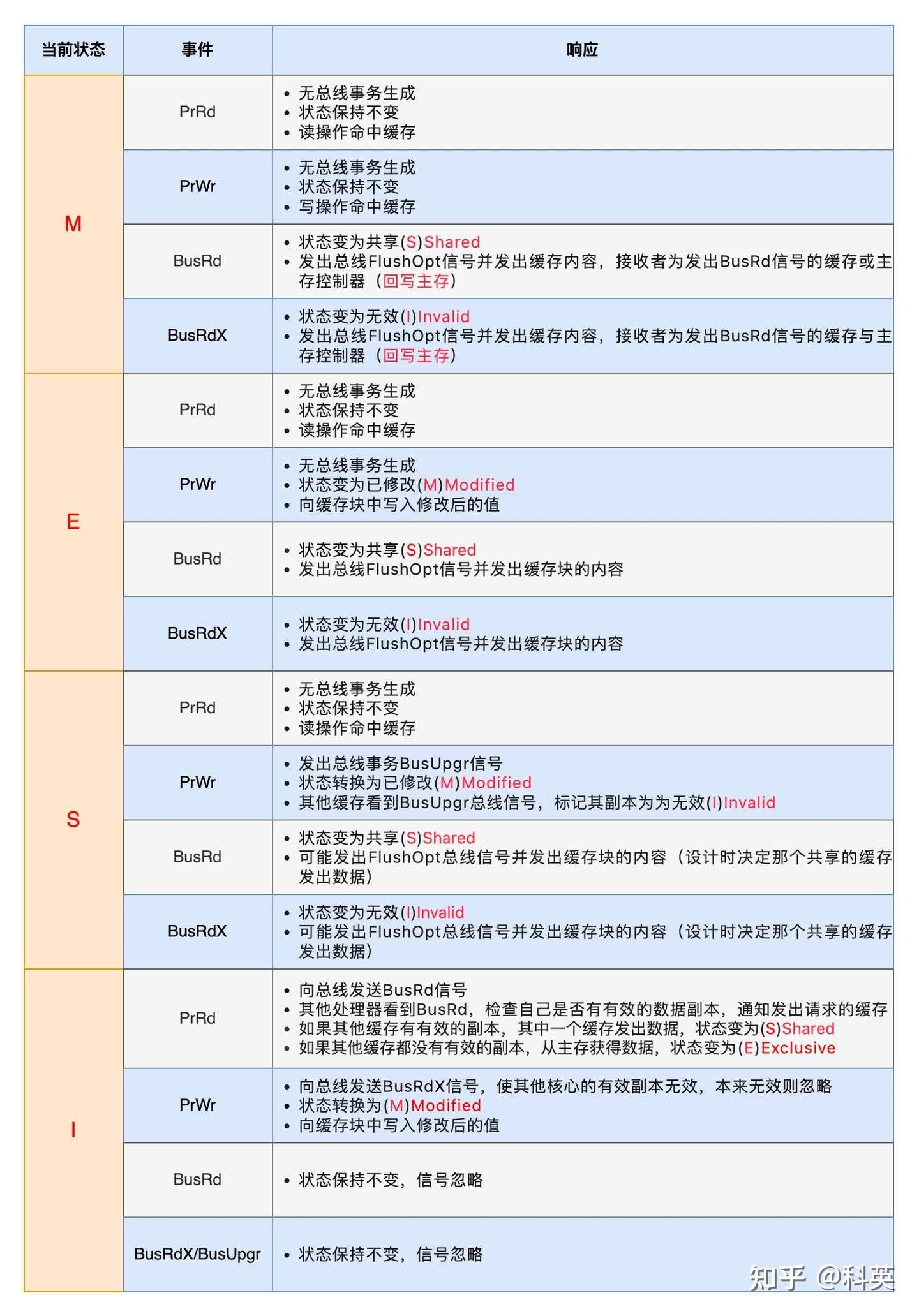
go 通过汇编学习atomic原子操作原理
文章目录 概要一、原理1.1、案例1.2、关键汇编 二、LOCK汇编指令2.1、 LOCK2.2、 原理2.2.1、 缓存行2.2.2、 缓存一致性之MESI协议2.2.3、lock原理 三、x86缓存发展四、x86 DMA发展参考 概要 在并发操作下,对一个简单的aa2的操作都会出错,这是因为这样…...

WebRTC 源码原生端Demo入门-1
1、概述 我的代码是比较新的,基于webrtc源码仓库的main分支的,在windows下把源码仓库下载好了后,用visual stdio 2022打开进行编译调试src/examples/peerconnection_client测试项目,主要是跑通这个demo来入手和调试,纯看代码很难…...

Nipype 简单使用教程
Nipype 简单使用教程 基础教程**一、Nipype 核心概念与工作流构建****1. 基本组件****2. 工作流构建步骤** **二、常用接口命令速查表****1. FSL 接口****2. FreeSurfer 接口****3. ANTS 接口****4. 数据处理接口** **三、高级特性与最佳实践****1. 条件执行(基于输…...

股票回购、股票减持和股票解禁对股票价格影响的综合分析
以下是关于股票回购、股票减持和股票解禁对股票价格影响的综合分析,结合了市场机制、财务指标及投资者行为等多维度因素: 一、股票回购对股价的影响 1. 正面影响 • 提升财务指标:回购减少流通股数量,在净利润不变的情况下&#…...

linux 三剑客命令学习
grep Grep 是一个命令行工具,用于在文本文件中搜索打印匹配指定模式的行。它的名称来自于 “Global Regular Expression Print”(全局正则表达式打印),它最初是由 Unix 系统上的一种工具实现的。Grep 工具在 Linux 和其他类 Unix…...

【MySQL】第二弹——MySQL表的增删改查(CRUD)
文章目录 🎓一. CRUD🎓二. 新增(Create)🎓三. 查询(Rertieve)📖1. 全列查询📖2. 指定列查询📖3. 查询带有表达式📖4. 起别名查询(as )📖 5. 去重查询(distinct)📖6. 排序…...

Springboot中如何自定义配置类
在 Spring Boot 中,自定义配置类是通过 Configuration 注解定义的类,用于替代传统的 XML 配置,管理 Bean 的创建和应用程序的设置。 1. 创建自定义配置类 (1) 基本配置类 使用 Configuration 注解标记类,并在其中定义 Bean 方法…...

基于zernike 拟合生成包裹训练数据-可自定义拟合的项数
可以看到拟合误差其实还是有很多的,但是这个主要是包裹噪声产生的,用到了github 上的zernike 库,直接pip install 一下安装就可以了 import numpy as np import matplotlib.pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D import matpl…...

大模型赋能:2D 写实数字人开启实时交互新时代
在数字化浪潮席卷全球的当下,人工智能技术不断突破创新,其中大模型驱动的 2D 写实数字人正成为实时交互领域的一颗新星,引领着行业变革,为人们带来前所未有的交互体验。 一、2D 写实数字人概述 2D 写实数字人是通过计算机图形学…...
