堆复习(C语言版)
目录
1.树的相关概念:
2.堆的实现
3.TopK问题
4.总结
1.树的相关概念:
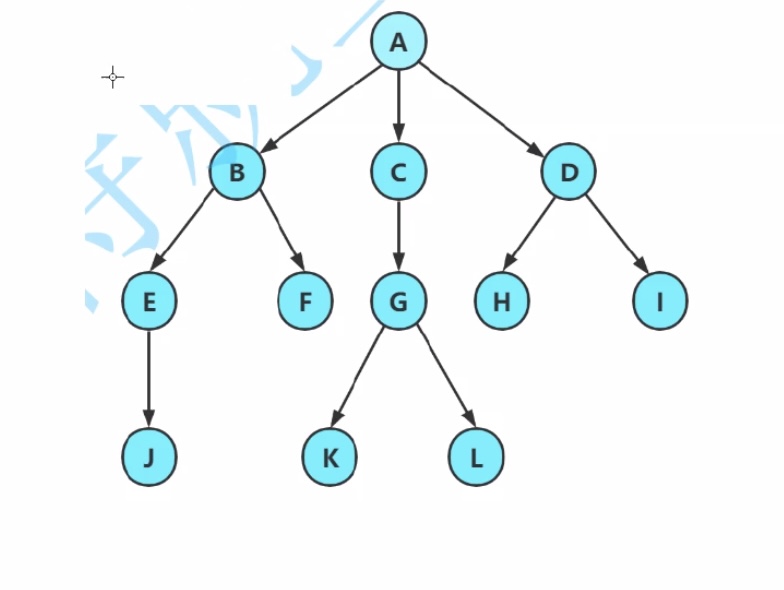
1.结点的度:一个结点含有的子树(孩子)个数。
A的度为6
2.叶结点or终端结点:度为0的结点。
J、K、L、H、I 都是叶子结点
3.非终端结点or分支结点:度不为0的结点
4.双亲结点or父结点:若一个结点含有子结点,那么这个结点被叫做该子结点的父结点。
5.孩子结点or子结点:和概念4反过来
A是B的父结点,B是A的子结点
6.兄弟结点:具有相同父结点的结点互称为兄弟结点
B、C、D是兄弟结点
7.堂兄弟结点:双亲在同一层的结点互为堂兄弟结点
E、F、G、H、I是堂兄弟结点
8.树的度:整棵树中最大的结点的度就是整棵树的度
树的度为3(即A的度,没有比A的度更大的)
9.树的层次:从根结点开始算,根为第1层(一般情况都是从第1层开始算,有些书本上也会从第0层开始算),其所有子节点为第2层,以此类推……
10.树的深度or高度:树中最大的层次
树的高度为4
11.结点的祖先:从根结点到该结点所经分支上的所有结点
L的祖先有G、C、A ,A是所有结点的祖先
12.子孙:和概念11反过来
L是G、C、A的子孙 ,所有结点都是A的子孙
13.森林:多棵互不相交的树组成的集合称为森林
14.一颗N个结点的树有N-1条边
15.对任何一棵二叉树,如果度为0的叶节点个数为m,度为2的分支结点个数为n,则有m = n+1
树的构建是用递归来实现的,把一整棵树看成一个根节点+几个子树,把子树看作一个子树的根节点+子树的子树,以此类推……,直到叶子结点
逻辑结构:想象出来的,例如二叉树就是典型的逻辑结构
物理结构(存储结构):实际编程时所使用的结构,数组、链表这些就是物理结构
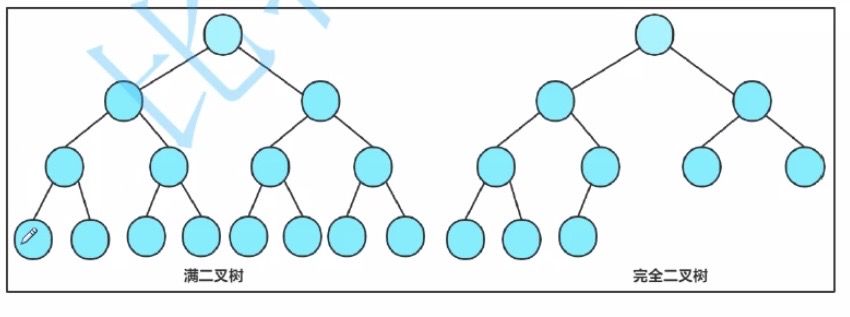
特殊的二叉树:
1.满二叉树:每一层都是满的二叉树
假设满二叉树树有N层
第一层 -> 2^0 个结点
第二层 -> 2^1 个结点
……
第N层 -> 2^(N-1)个结点
sum(1+2+……+N) = 2^0 + 2^1 + …… + 2^(N-1) = 2^N - 1 (等比数列求和)
假设满二叉树共有H个结点
2^N - 1 = H ,N = log2(H+1)
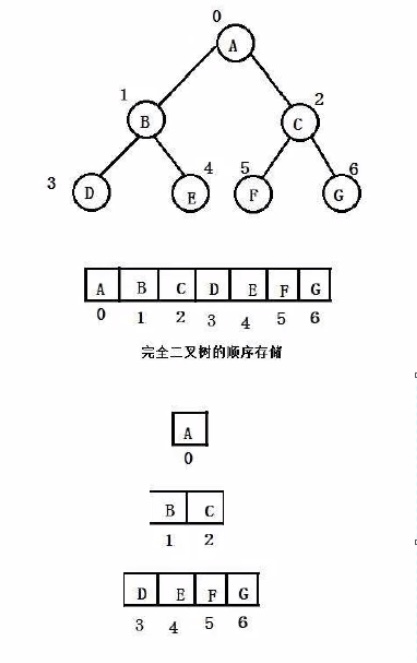
2.完全二叉树:前 N - 1 层都是满的,最后一层不满且从左到右必须是连续的
当我们用数组实现完全二叉树时(只有完全二叉树、满二叉树可以用数组实现,否则数组中有些下标对应的元素为空,会存在大量的空间浪费)
假设父亲在数组中的下标:i
左孩子在数组中的下标:2*i + 1
右孩子在数组中的下标:2*i + 2
假设孩子在数组中的下标:j
父亲在数组中的下标:( j-1 ) / 2
因为 "(4-1) / 2 = (4-2) / 2 ",所以不用区分是左孩子还是右孩子
2.堆的实现
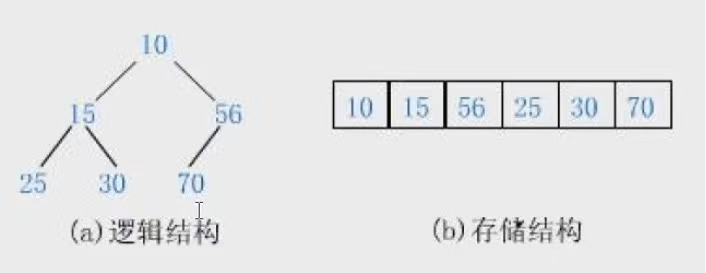
堆是一个完全二叉树,堆分为了大根堆(任何一个父亲≥孩子)、小根堆(任何一个父亲≤孩子)
上图所示的即为小根堆
题1:
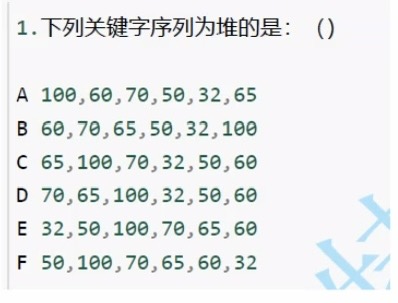
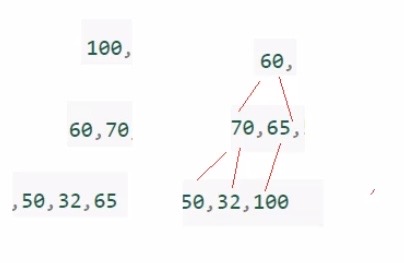
该类题目先是按照完全二叉树的概念,拆分成h层,然后看上下两层的元素是否都满足同一种大小关系
A选项中,即使60<65,但是70大于65,依旧满足大根堆的概念
B选项中,100大于上一层中的任何一个元素,所以不是堆
……
答案为A
void Adjustup(int* a, int child) //此处的child和parents都是表示数组的下标
{//初始化双亲结点int parents = (child - 1) / 2;while (child > 0){if (a[child] < a[parents])//小根堆{Swap(&a[child], &a[parents]);//改变两个元素的位置child = parents;parents = (child - 1) / 2;}else break;}
}void AdjustDown(int* a,int n, int parent)
{//先假设左孩子小int child = parent * 2 + 1;//如果child >= size(n),说明已经到了叶子节点,停止循环while (child < n){//找出小的那个孩子(先得判断有没有右孩子,这也就是假设左孩子小,不假设右孩子小的原因)if (child + 1 < n && a[child + 1] < a[child])child++;//右孩子比较小,改为右孩子//交换or不交换位置,父节点小于小的子节点时,说明找到了该在的位置if (a[parent] <= a[child]) break;else{Swap(&a[parent],&a[child]);parent = child;child = parent * 2 + 1;}}
}

向上调整、向下调整算法是实现堆还有堆排序最重要的一个算法
AdjustUp函数(上图1):
每次有新的元素插入到二叉树(也可以看作是数组)以后,每次都进行结点和父节点的比较,直到该结点比父节点小时停止位置交换(上图是push函数的流程图,push函数用到的就是向下调整)
AdjustDown函数(上图2):
比较父结点的2个子节点的大小,和小的那个子节点交换位置,这样最后放在上一层的结点要比原兄弟结点和原父节点的元素都小,同时可以保证根节点永远是整个数组中最小的(上图是pop函数的流程图,pop函数用到的就是向下调整)
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef struct heap
{int* a;int size;int capacity; // 当结点数量很多时,可能需要扩容
}hp;void Adjustup(int* a, int child);
void AdjustDown(int* a, int n, int parent);
void HPInit(hp* php);
void HPDestroy(hp* php);
void HPPush(hp* php, int x);
void HPPop(hp* php);
int HPTop(hp* php);
bool HPEmpty(hp* php);
void HPDestory(hp* php);
//heap.h#include"heap.h"void HPInit(hp* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;
}
void HPDestroy(hp* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}
void Swap(int* a, int* b)
{int c = *a;*a = *b;//把a地址处的元素变为b位置处的元素*b = c;
}
void Adjustup(int* a, int child) //此处的child和parents都是表示数组的下标
{//初始化双亲结点int parents = (child - 1) / 2;while (child > 0){if (a[child] < a[parents])//小根堆{Swap(&a[child], &a[parents]);//改变两个元素的位置child = parents;parents = (child - 1) / 2;}else break;}
}
void HPPush(hp* php, int x)
{ //扩容or初始化if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;int* temp = (int*)realloc(php->a, sizeof(int) * newcapacity);if (!temp){perror("realloc failure");return;}php->a = temp;php->capacity = newcapacity;}//开始插入php->a[php->size++] = x;//开始向上调整Adjustup(php->a, php->size-1);
}
void AdjustDown(int* a,int n, int parent)
{//先假设左孩子小int child = parent * 2 + 1;//如果child >= size(n),说明已经到了叶子节点,停止循环while (child < n){//找出小的那个孩子(先得判断有没有右孩子,这也就是假设左孩子小,不假设右孩子小的原因)if (child + 1 < n && a[child + 1] < a[child])child++;//右孩子比较小,改为右孩子//交换or不交换位置,父节点小于小的子节点时,说明找到了该在的位置if (a[parent] <= a[child]) break;else{Swap(&a[parent],&a[child]);parent = child;child = parent * 2 + 1;}}
}void HPPop(hp* php)
{assert(php);assert(php->a > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}bool HPEmpty(hp* php)
{assert(php);return php->size == 0;
}int HPTop(hp* php)
{assert(php);assert(php->size > 0);return php->a[0];
}void HPDestory(hp* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}
//heap.c#include"heap.h"void Test1()
{//根据堆的特性,每次输出根节点以后,把根节点删除后重复刚才的操作,那么输出的结果就是有序的int a[] = { 4,2,9,7,5,6,8,3,1 };hp HP;HPInit(&HP);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&HP,a[i]);}int i = 0;while (!HPEmpty(&HP)) //非空就不断执行{printf("%d ", HPTop(&HP));HPPop(&HP);}HPDestory(&HP);printf("\n");
}void HPSort(int* a,int n)
{//for (int i = 1; i < n; i++)//Adjustup(a, i); //向上调整建立小堆操作,时间复杂度为nlognfor (int i = (n - 1 - 1) / 2; i >= 0; i--)AdjustDown(a, n, i);//从最后一个父节点开始,依次向下调整,直到调整到根节点为止,时间复杂度为nint end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0); end--;}
}void Test2()
{int a[] = { 4,2,9,7,5,6,8,3,1 };HPSort(a, sizeof(a) / sizeof(int));for (int i = 0; i <= 8; i++) printf("%d ", a[i]);printf("\n");
}int main()
{Test1();Test2();return 0;
}
//test.C代码重点讲解:
HPPush函数:
在物理结构中,插入操作是插入在数组的后面
假设是小根堆,元素x插入j下标位置时,如果(j-1)/2下标位置处的元素y小于x,那么直接插入;否则就先插入,然后两者互换位置,再对互换完位置的x与上面的父结点y相比较,重复刚才的操作
最坏情况可能要和根节点交换位置
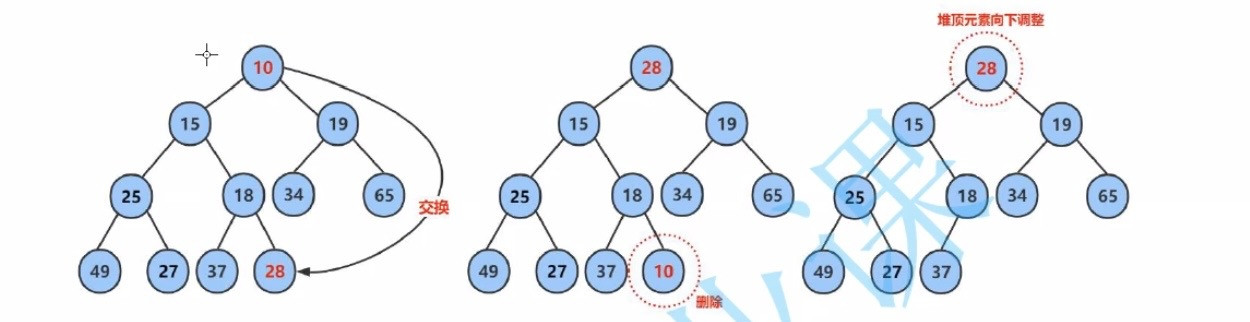
HPPop函数:
不能直接数组所有元素向前1位,如此操作兄弟结点可能变为了父节点,堆关系大概率就不存在了
因此可以把要删除的元素和最后一个元素进行交换,删除数组最后一个元素对整个堆不会有任何影响
然后把换了位置后的元素进行向下调整(向上调整的逆操作),向下调整是因为他原本所在最后一层,会是一个比较大or比较小元素(大小根堆的不同)用作删除堆顶的数据(即根节点的数据),每次删除的元素都是最大or最小的元素(堆的特性)
下图1为流程图
HPSort函数:
把数组直接看成一棵二叉树,然后把二叉树中所有元素(除根节点外)进行一次向上调整,每个元素就能找到他们应该存在的位置,这样就能直接把无序数组搞成一个堆了(代码如下图2);但由于这样操作,从根节点到叶子节点的所有数据都要向上调整一次,而叶子节点的向上调整次数最多可以占到所有向上调整次数的半数以上,所以我们此处进行了一定的优化(优化成向下调整)
创建小堆:如果要把数组中的元素进行降序排序,先建立一个小堆,然后进行类似于HPPop的操作(第一个元素和最后一个元素交换位置,然后把当前第一个元素向下调整,如此就能第一个元素(根节点元素)永远是最小的),这样即可完成操作;从最后一个父节点开始,依次向下调整,直到调整到根节点为止,因为叶子节点向下调整也没有东西可以调了,并且最后一层叶子节点(如果是满二叉树),那么叶子结点的函数调用次数将占到所有调用次数的50%,因此从最后一个父节点开始遍历是很大的优化
排序:排完小根堆以后,根节点就是最小值了,此时将根节点与末尾元素交换,每次再对交换上来的末尾元素向下调整(保持小堆特性),就能保住根节点永远是最小的,这样放到末尾的肯定也是最小的;将一个最小的元素放在了末尾以后,下标需要不断往前推移(因为当某个元素放在末尾以后,位置就不需要再进行改动了),直到下标为0时(下标为0时,所有元素都已经排序完毕了,不需要再对已经排完序的数组进行一次操作了),时间复杂度为nlogn
注:若使用大根堆,则此时最头部的元素为最大值;那假设我们把最大值放在最后,然后把所有数据往前移动1位(数组视角),覆盖掉前面数据,再对最头部的元素进行向下调整(保持大根堆特性),这是否可行?
答:这是不可行的,因为数组是被看作完全二叉树的,往前覆盖时结点与结点之间的关系发生了改变(兄弟节点变成了子节点,父结点变成了祖先结点)(如下图3)
代码实现的是降序排序,如果要把降序改为升序就把AdjustDown中的 “a[child + 1] < a[child]” 和 “a[parent] <= a[child]”改为 “a[child + 1] > a[child]” 和 “a[parent] >= a[child]”记忆方法:降序小堆、升序大堆(降小升大)


插入删除结点时,向上向下调整算法的时间复杂度为什么是O(logN)?
如上图所示,完全二叉树的层数近似于log2(N),因此无论是向上还是向下调整的次数都为log2(N)次,所以时间复杂度为O(logN)
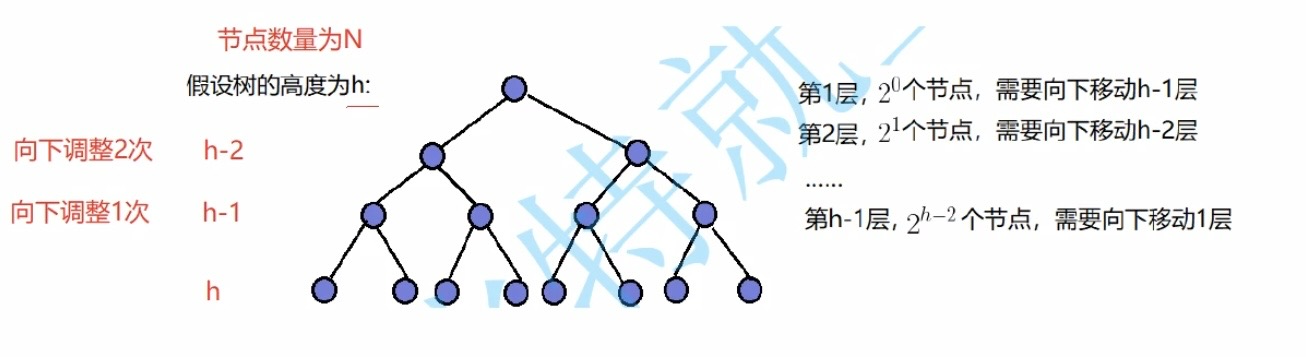
使用向下调整算法完成建堆操作时,为什么时间复杂度为O(N)?
如下图所示(向下调整指的是最大向下调整次数),根据数学归纳法不难得出
T(h) = 2^0 * (h-1) + 2^1 * (h-2) + …… + 2^(h-3) * 2 + 2^(h-2) * 1
T(h)计算向下调整建堆最坏情况下合计的调整次数
从后往前看,第h-1层有2^(h-2)个结点,最多向下调整1次……(以此类推,得出该式)
对该式进行错位相减法,具体操作如下所示:
2 * T(h) = 2^1 * (h-1) + 2^2 * (h-2) + …… + 2^(h-2) * 2 + 2^(h-1) * 1 = D(h)
D(h) - T(h) = 2^1 + 2^2 + …… + 2^(h-2) + 2^(h-1) * 1 - 2^0*(h-1) = T(h)
错位相减法使用说明:以 2^1*(h-1) 和 2^1*(h-2) 为例,最后结果为 2^1 ;因为两式的 2^(x) 系数不同但系数的差值恒为1,所以后续都只保留 2^(x) 部分 ;然后再把剩下的没有对应式子的抄下来即可
- 2^0*(h-1) = 2^0 - 2^0*h
2^(h-1) * 1 = 2^(h-1)
F(h) = 2^h - 1 = N (高度为h的满二叉树的结点个数)
T(h) = 2^h - 1 - h = N - h -> 时间复杂度为O(N)
为什么向上调整算法实现建堆时间复杂度远高于向下调整算法?
向上调整:结点数量多的层 * 调整次数多(最后一层需要最多次调整)
结点数量少的层 * 调整次数少
向下调整:结点数量多的层 * 调整次数少(最后一层不需要调整)
结点数量少的层 * 调整次数多
3.TopK问题

方法1:
建立一个N个数的大堆 O(N)
top pop k次 O(k*logN) = O(logN)
如果有10亿个整数数据(40亿字节)建堆,那么需要多少内存空间?
4GB = 4*1024MB = 4*1024*1024KB = 4*1024*1024*1024Byte > 40亿Byte ,因此需要用不到4G的内存去存储10亿个整型数据,内存条倍感压力……
假设只有1G内存,那么可以每次只对1G的数据内容找最大的k个,进行了 x(x = sumGB/1GB)该操作后,在找到的 x*k 个数据中再去找最大的k个
但假设只有1M甚至1K内存,那么这样的操作时间复杂度就过高了
由于不是内存空间占用过大,就是时间复杂度过高,因此该方法并不优秀
方法2:
用数据中的前k个数,建一个小堆;剩下的N-k个数依次与栈顶数据进行比较,如果比栈顶的数据大,就代替栈顶进堆(覆盖根位置,然后向下调整);遍历完以后小堆里的k个数,就是最大的k个数
k个数的完全二叉树创建,时间复杂度为logk;对剩余数据进行遍历,时间复杂度为N-k
总的时间复杂度:logk * (N-k) = O(N)
#include"heap.h"void TopK(int k) //解决topK问题,即从N个数中找最大的前k个(类似于现实中的游戏排行榜)
{int a[] = { 4,2,9,7,5,6,8,3,1 };//创建k个数据的小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--)AdjustDown(a, k, i);int i = k;//对剩下的N-k个数据进行遍历while (i < sizeof(a) / sizeof(int)){if (a[0] < a[i]){//覆盖数据a[0] = a[i];//在小堆中向下调整AdjustDown(a, k, 0);i++;}else //比最小的小,直接跳过不用放入堆中{i++;continue;}}for (int i = 0; i <= k - 1; i++)printf("%d ", a[i]);
}int main()
{TopK(3);return 0;
}
//test.c代码重点讲解:
创建小堆时,直接在数组中进行创建;堆有k个元素,映射到数组下标就是k-1;把[0,k-1]下标的数组看作完全二叉树,创建时直接从最后的父节点开始依次向下调整,最后的父节点根据完全二叉树子节点与父节点关系公式: (j-1)/2 = i ,可以得出下标为 (k - 1 - 1)/2
然后再对原数组[k,n-1]下标的元素进行遍历,其余操作如上文所述
4.总结
1.堆---数据结构---C++stl库中的priority_queue
2.堆排序
3.topK问题
4.堆排序、topK的时间复杂度问题
相关文章:

堆复习(C语言版)
目录 1.树的相关概念: 2.堆的实现 3.TopK问题 4.总结 1.树的相关概念: 1.结点的度:一个结点含有的子树(孩子)个数。 A的度为6 2.叶结点or终端结点:度为0的结点。 J、K、L、H、I 都是叶子结点 3.非终端结…...

Spring AI 与 Groq 的深度集成:解锁高效 AI 推理新体验
Spring AI 与 Groq 的深度集成:解锁高效 AI 推理新体验 前言 在人工智能飞速发展的当下,AI 推理的效率和性能成为开发者关注的焦点。Groq 作为一款基于 LPU™ 的超快速 AI 推理引擎,凭借其强大的性能,能够支持各类 AI 模型&…...

Megatron系列——张量并行
本文整理自bilibili Zomi视频 1、行切分和列切分 注意: (1)A按列切分时,X无需切分,split复制广播到A1和A2对应设备即可。最后Y1和Y2需要拼接下,即All Gather (2)A按行切分时&#…...

学习笔记:黑马程序员JavaWeb开发教程(2025.4.3)
12.1 基础登录功能 EmpService中的login方法,是根据接收到的用户名和密码,查询时emp数据库中的员工信息,会返回一个员工对象。使用了三元运算符来写返回 Login是登录,是一个业务方法,mapper接口是持久层,是…...

DeepSeek的100个应用场景
在春节前夕,浙江杭州的AI企业DeepSeek推出了其开源模型DeepSeek-R1,以仅相当于Open AI最新模型1/30的训练成本,在数学、编程等关键领域展现出媲美GPT-o1的出色性能。发布仅数日,DeepSeek-R1便迅速攀升至中美两国苹果应用商店免费榜…...

[Windows] Honeyview V5.53
[Windows] Honeyview 链接:https://pan.xunlei.com/s/VOQ3BzcINSmMb1YsHO_Pp2tqA1?pwdujkm# Honeyview是一款兼快速与强大于一体的免费图像查看器, 本版本为该软件的最后一个版本,将不再有新的更新。 主要功能 轻量且快速可以显示包括…...

VUE3基础样式调整学习经验
首先创建一个vue项目最好要把不属于自己的样式都删除掉,以面出现css难以调整的情况: 1.assets目录下的main.css、base.css等样式全部删除 2.app.vue下的样式也全部删除 3.使用element plus一定要加入样式包: import element-plus/dist/in…...

Altera系列FPGA实现图像视频采集转HDMI/LCD输出,提供4套Quartus工程源码和技术支持
目录 1、前言工程概述免责声明 2、相关方案推荐我已有的所有工程源码总目录----方便你快速找到自己喜欢的项目Altera系列FPGA相关方案推荐 3、设计思路框架工程设计原理框图输入Sensor之-->OV7725摄像头输入Sensor之-->OV5640摄像头输入Sensor之-->串口传图输入图像缓…...

互联网大厂Java面试实战:Spring Boot到微服务的技术问答解析
💪🏻 1. Python基础专栏,基础知识一网打尽,9.9元买不了吃亏,买不了上当。 Python从入门到精通 😁 2. 毕业设计专栏,毕业季咱们不慌忙,几百款毕业设计等你选。 ❤️ 3. Python爬虫专栏…...

Leetcode-BFS问题
LeetCode-BFS问题 1.Floodfill问题 1.图像渲染问题 [https://leetcode.cn/problems/flood-fill/description/](https://leetcode.cn/problems/flood-fill/description/) class Solution {public int[][] floodFill(int[][] image, int sr, int sc, int color) {//可以借助另一…...

Web端项目系统访问页面很慢,后台数据返回很快,网络也没问题,是什么导致的呢?
Web端访问缓慢问题诊断指南(测试工程师专项版) ——从浏览器渲染到网络层的全链路排查方案 一、问题定位黄金法则(前端性能四象限) 1. [网络层] 数据返回快 ≠ 资源加载快(检查Content Download时间) 2. [渲染层] DOM复杂度与浏览器重绘(查看FPS指标) 3. [执行层…...

Next.js 知识框架总结
一、核心概念 1. 渲染策略 CSR (Client-Side Rendering): 传统 React 渲染方式 SSR (Server-Side Rendering): 服务端渲染 getServerSideProps SSG (Static Site Generation): 静态生成 getStaticProps getStaticPaths (动态路由) ISR (Incremental Static Regeneration…...

【PostgreSQL数据分析实战:从数据清洗到可视化全流程】8.4 数据故事化呈现(报告结构设计/业务价值提炼)
👉 点击关注不迷路 👉 点击关注不迷路 👉 点击关注不迷路 文章大纲 8.4 数据故事化呈现:从报告结构到业务价值的深度融合一、数据故事化的核心价值体系(一)报告结构设计的黄金框架1. 业务场景锚定ÿ…...

专题二:二叉树的深度搜索(二叉树剪枝)
以leetcode814题为例 题目分析: 也就是当你的子树全为0的时候就可以剪掉 算法原理分析: 首先分析问题,你子树全为0的时候才可以干掉,我们可以设递归到某一层的时候如何处理 然后抽象出三个核心问题 也就是假设我们递归到第2层…...

Hugging Face推出了一款免费AI代理工具,它能像人类一样使用电脑
Hugging Face推出了一款免费AI代理工具,它能像人类一样使用电脑。 这款工具名为Open Computer Agent(开放计算机代理),可模拟真实的电脑操作。 无需安装,在浏览器中即可运行。 以下是一些信息: - Open C…...

Datawhale AI春训营 day
待补充 2025星火杯应用赛入门应用 创空间 魔搭社区 {"default": {"system": "你是星火大模型,一个由科大讯飞研发的人工智能助手。请用简洁、专业、友好的方式回答问题。","description": "默认系统提示词"}…...

Java面试高阶篇:Spring Boot+Quarkus+Redis高并发架构设计与性能优化实战
Java面试高阶篇:Spring BootQuarkusRedis高并发架构设计与性能优化实战 面试官(严肃): Q1: 你项目中如何实现高并发下的缓存优化? 候选人(水货): 我们用了Redis做缓存,…...

生成对抗网络(GAN)深度解析:理论、技术与应用全景
生成对抗网络(Generative Adversarial Networks,GAN)作为深度学习领域的重要突破,通过对抗训练框架实现了强大的生成能力。本文从理论起源、数学建模、网络架构、工程实现到行业应用,系统拆解GAN的核心机制,涵盖基础理…...

CSRF记录
CSRF(Cross-site request forgery)跨站请求伪造:攻击者诱导受害者进入第三方网站,在第三方网站中,向被攻击网站发送跨站请求。利用受害者在被攻击网站已经获取的注册凭证,绕过后台的用户验证,达…...

【ROS2】CMakeLists配置信息通俗解释
文件示例 cmake_minimum_required(VERSION 3.8) project(pkg01_helloworld_cpp)if(CMAKE_COMPILER_IS_GNUCXX OR CMAKE_CXX_COMPILER_ID MATCHES "Clang")add_compile_options(-Wall -Wextra -Wpedantic) endif()# find dependencies find_package(ament_cmake REQU…...

Python集成开发环境之Thonny
前言:今天介绍一款Python的傻瓜IDE(集成开发环境)——Thonny,比较适合初学者进行Python程序的开发和学习,为用户提供了代码编辑、调试、运行等一系列功能。 我应该不止两次提到过这个词了“IDE”(集成开发环境)&#…...
【超详细教程】安卓模拟器如何添加本地文件?音乐/照片/视频一键导入!
作为一名安卓开发者或手游爱好者,安卓模拟器是我们日常工作和娱乐的重要工具。但很多新手在使用过程中常常遇到一个共同问题:**如何将电脑本地的音乐、照片、视频等文件导入到安卓模拟器中?**今天,我将为大家带来一份全网最详细的…...

switch能否作用在byte上,long上,string上
在Java中,switch语句可以用于多种数据类型,但这些类型需要满足特定的条件。以下是switch语句可以作用的数据类型: byte:可以用于switch语句。由于byte可以隐式转换为int,所以可以直接在switch语句中使用。 long&#…...

构建DEEPPOLAR ——Architecture for DEEPPOLAR (256,37)
目录 编码器 解码器 编码器 编码器是大小为的内核的集合ℓ 16,每个都由神经网络g建模。编码器内核g负责编码ℓ 输入。g的架构如下: 表1 DEEPOLAR模型训练中使用的超参数(256,37,ℓ16) Table 1. Hyperparameters used in model…...
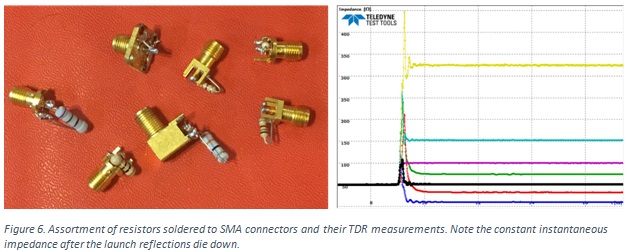
使用 DMM 测试 TDR
TDR(时域反射计)可能是实验室中上升时间最快的仪器,但您可以使用直流欧姆表测试其准确性。 TDR 测量什么 在所有高速通道中,反射都很糟糕。我们尝试设计一个通道来减少反射,这些反射都会导致符号间干扰 (…...

客户端限流主要采用手段:纯前端验证码、禁用按钮、调用限制和假排队
一、纯前端验证码 场景 防止机器人或脚本高频提交,需用户完成验证后才能触发请求。 Vue 前端实现 <template><div><button click"showCaptcha">提交订单</button><div v-if"captchaVisible"><img :src"…...

第一天——贪心算法——分饼干
一、算法介绍 顾名思义,贪心算法或贪心思想采用贪心的策略,保证每次操作都是局部最优的,从而使最后得到的结果是全局最优的。 举一个最简单的例子:小明和小王喜欢吃苹果,小明可以吃五个,小王可以吃三个。…...

企业数字化中台建设方案(AI/技术中台、数据中台、业务中台)
构建企业数字化中台需要实现业务、数据、AI和技术四大中台的有机协同,形成闭环能力体系。以下是综合建设方案(含技术架构和实施路径): 一、建设背景与目标 1.1 行业痛点 生产设备数据孤岛,实时监控能力不足 传统ERP/…...

单因子实验方差分析模型的适应性检验
本文是实验设计与分析(第6版,Montgomery著傅珏生译)第3章单因子实验 方差分析第3.4节的python解决方案。本文尽量避免重复书中的理论,着于提供python解决方案,并与原书的运算结果进行对比。您可以从Detail 下载实验设计与分析&…...

linux CUDA与CUDNN安装教程
目录 1.CUDA安装 1.1.CUDA作用 1.2.CUDA下载 1.3.CUDA安装 1.4.验证 2.CUDNN安装 2.1.CUDNN作用 2.2.下载 2.3.安装 2.4.验证 1.CUDA安装 1.1.CUDA作用 CUDA 是 NVIDIA 提供的并行计算平台和编程模型,允许开发者直接利用 GPU 的并行计算能力ÿ…...
