电能质量扰动信号信号通过hilbert变换得到瞬时频率
利用Hilbert变换从电能质量扰动信号中提取瞬时频率、瞬时幅值、Hilbert谱和边际谱的详细步骤及MATLAB代码实现。该流程适用于电压暂降、暂升、谐波、闪变等扰动分析。
1. Hilbert变换与特征提取流程
1.1 基本步骤
- 信号预处理:滤波去噪(如小波去噪)或经验模态分解(EMD)提取主成分。
- Hilbert变换:计算解析信号,得到瞬时幅值和相位。
- 瞬时频率计算:对相位求导得到瞬时频率。
- Hilbert谱与边际谱:时频能量分布及频率能量累积。
1.2 数学公式
- 解析信号:
[
z(t) = x(t) + j \mathcal{H}[x(t)]
]
其中 (\mathcal{H}) 为Hilbert变换。 - 瞬时幅值:
[
A(t) = |z(t)|
] - 瞬时相位:
[
\phi(t) = \arctan\left(\frac{\mathcal{H}[x(t)]}{x(t)}\right)
] - 瞬时频率:
[
f(t) = \frac{1}{2\pi} \frac{d\phi(t)}{dt}
] - Hilbert谱:时频平面上的幅值分布 (H(f, t))。
- 边际谱:
[
h(f) = \int_{0}^{T} H(f, t) dt
]
2. MATLAB代码实现
2.1 信号生成(示例为含暂降的电压信号)
fs = 10e3; % 采样率10 kHz
t = 0:1/fs:0.1; % 时间序列(0.1秒)
f0 = 50; % 基频50 Hz
A_normal = 1; % 正常幅值
A_sag = 0.5; % 暂降幅值% 生成含暂降的电压信号(暂降发生在0.03s-0.07s)
x = A_normal * sin(2*pi*f0*t);
x(t >= 0.03 & t <= 0.07) = A_sag * sin(2*pi*f0*t(t >= 0.03 & t <= 0.07));% 添加噪声(SNR=30dB)
x = awgn(x, 30, 'measured');% 绘制原始信号
figure;
plot(t, x);
xlabel('Time (s)');
ylabel('Voltage (pu)');
title('含暂降的电压信号(加噪)');
2.2 预处理(EMD分解去噪)
% 经验模态分解(需安装Signal Processing Toolbox)
imf = emd(x, 'Interpolation', 'pchip');% 选择前2个IMF作为主成分(假设噪声主要在高频IMF)
x_denoised = sum(imf(:,1:2), 2);% 绘制去噪后信号
figure;
plot(t, x_denoised);
title('去噪后的电压信号(EMD)');
2.3 Hilbert变换与瞬时特征提取
% 计算解析信号
z = hilbert(x_denoised);% 提取瞬时幅值和相位
A = abs(z); % 瞬时幅值
phi = unwrap(angle(z)); % 瞬时相位(解卷绕)% 计算瞬时频率
f_inst = diff(phi) / (2*pi) * fs;
f_inst = [f_inst(1), f_inst]; % 保持长度一致% 绘制瞬时特征
figure;
subplot(3,1,1);
plot(t, A);
title('瞬时幅值');
subplot(3,1,2);
plot(t, phi);
title('瞬时相位');
subplot(3,1,3);
plot(t, f_inst);
ylabel('Frequency (Hz)');
title('瞬时频率');
2.4 Hilbert谱与边际谱计算
% 时频分析参数
nfft = 1024; % FFT点数
window = hann(256); % 窗函数
noverlap = 128; % 重叠点数% 计算Hilbert谱(基于短时傅里叶变换STFT)
[S, f, t_spec] = spectrogram(A, window, noverlap, nfft, fs);% 绘制Hilbert谱
figure;
imagesc(t_spec, f, 20*log10(abs(S)));
axis xy;
colorbar;
xlabel('Time (s)');
ylabel('Frequency (Hz)');
title('Hilbert能量谱');% 计算边际谱(频率能量累积)
h = sum(abs(S), 2);% 绘制边际谱
figure;
plot(f, h);
xlabel('Frequency (Hz)');
ylabel('Energy');
title('边际谱');
3. 关键特征解释
3.1 瞬时幅值
- 正常状态:幅值稳定在标称值(如1 pu)。
- 暂降期间:幅值显著降低(如0.5 pu),直接反映扰动强度。
3.2 瞬时频率
- 正常状态:频率围绕基频(50/60 Hz)小幅波动。
- 扰动期间:频率可能出现突变(如电压暂降伴随频率偏移)。
3.3 Hilbert谱
- 时频分布:显示不同时间点各频率成分的能量强度。
- 暂降特征:在扰动时段(0.03s-0.07s),基频能量降低,可能伴随高频噪声。
3.4 边际谱
- 能量累积:反映信号在整个时间段内的频率能量分布。
- 暂降分析:基频能量减少,高频成分可能增加(噪声或谐波)。
4. 改进与扩展
4.1 多扰动类型特征提取
针对不同扰动类型(如谐波、闪变),可设计专用特征:
- 谐波畸变:边际谱中基频倍频处出现峰值。
- 电压闪变:瞬时幅值呈现周期性波动。
% 谐波检测示例:检查边际谱中2f0、3f0处能量
harmonics = [2*f0, 3*f0];
[~, idx] = min(abs(f - harmonics), [], 2);
harmonic_energy = h(idx);
4.2 结合机器学习分类
将Hilbert特征输入分类模型(如SVM、LSTM):
% 构造特征向量(示例)
features = [max(A), min(A), mean(f_inst), std(f_inst), max(h)];% 使用SVM分类(需Statistics and Machine Learning Toolbox)
load('fault_data.mat'); % 假设已标记数据集
model = fitcsvm(X_train, y_train);
y_pred = predict(model, X_test);
4.3 实时监测实现
使用滑动窗口处理实时数据流:
window_length = 0.02 * fs; % 20ms窗口
for i = 1:length(x)-window_lengthx_window = x(i:i+window_length-1);% 执行Hilbert变换和特征提取...
end
5. 注意事项
- 端点效应:Hilbert变换在信号两端易产生畸变,可通过镜像延拓缓解。
- 模态混叠:EMD分解时若出现模态混叠,可改用EEMD或CEEMDAN。
- 噪声敏感:强噪声环境下需结合小波阈值去噪或变分模态分解(VMD)。
- 计算效率:实时应用时需优化STFT窗口长度和重叠率。
matlab实现代码
通过上述代码和分析,可有效提取电能质量扰动信号的Hilbert时频特征,为故障诊断、分类和定位提供关键信息。实际应用中需根据具体扰动类型调整参数并验证特征有效性。
相关文章:

电能质量扰动信号信号通过hilbert变换得到瞬时频率
利用Hilbert变换从电能质量扰动信号中提取瞬时频率、瞬时幅值、Hilbert谱和边际谱的详细步骤及MATLAB代码实现。该流程适用于电压暂降、暂升、谐波、闪变等扰动分析。 1. Hilbert变换与特征提取流程 1.1 基本步骤 信号预处理:滤波去噪(如小波去噪&…...
)
Linux工作台文件操作命令全流程解析(高级篇之awk精讲)
全文目录 1 工具介绍2 核心优势3 命令格式3.1 命令格式说明3.2 组成部分详解3.2.1 选项3.2.2 模式3.2.3 动作3.2.4 输入文件 4 使用说明4.1 常用示例4.2 awk 编程解析4.2.1 基础说明4.2.2 编程进阶 4.3 温馨提示 5 内置变量6 参考文献 写在前面 前面一篇《Linux工作台文件操作命…...
力扣119题:杨辉三角II(滚动数组)
小学生一枚,自学信奥中,没参加培训机构,所以命名不规范、代码不优美是在所难免的,欢迎指正。 标签: 杨辉三角、滚动数组 语言: C 题目: 给定一个非负索引 rowIndex,返回「杨辉三角…...
)
c++:算法(Algorithms)
目录 常用 STL 算法 1️⃣ std::sort(排序) 2️⃣ std::find(查找等于某值的元素) 3️⃣ std::count(统计出现次数) 4️⃣ std::next(获取迭代器的下一个位置) 5️⃣ .erase(…...

大疆无人机(全系列,包括mini)拉流至电脑,实现直播
参考视频 【保姆级教程】大疆无人机rtmp推流直播教程_哔哩哔哩_bilibili VLC使用教程: VLC工具使用指南-CSDN博客 目录 实现效果: 电脑端 编辑 编辑 无人机端 VLC拉流 分析 实现效果: (实验机型:大疆mini4kRC-N2遥控器、大…...

uniapp-商城-54-后台 新增商品(页面布局)
后台页面中还存在商品信息的添加和修改等。接下来我们逐步进行分析和展开。包含页面布局和数据库逻辑等等。 1、整体效果 样式效果如下,依然采用了表单形式来完成和商家信息差不多,但在商品属性上多做了一些弹窗等界面,样式和功能点表多。 …...

深入浅出MySQL 8.0:新特性与最佳实践
MySQL作为开源关系型数据库的佼佼者,近年来持续更新迭代,尤其是在8.0版本中引入了一系列令人兴奋的新特性。本文将介绍一些MySQL 8.0的关键新功能,并提供最佳实践,旨在帮助开发人员和DBA更好地利用这一强大的数据库管理系统。 一…...

JIT+Opcache如何配置才能达到性能最优
首先打开php.ini文件,进行配置 1、OPcache配置 ; 启用OPcache opcache.enable1; CLI环境下启用OPcache(按需配置) opcache.enable_cli0; 预加载脚本(PHP 7.4,加速常用类) ; opcache.preload/path/to/prel…...
python开发经验)
(2)python开发经验
文章目录 1 pyside6加载ui文件2 使用pyinstaller打包 更多精彩内容👉内容导航 👈👉Qt开发 👈👉python开发 👈 1 pyside6加载ui文件 方法1: 直接加载ui文件 from PySide6.QtWidgets import QAp…...

WebpackVite总结篇与进阶
模块化 Webpack Webpack 入口entry 分离app和第三方库入口 这是什么? 这是告诉 webpack 我们想要配置 2 个单独的入口点(例如上面的示例)。 为什么? 这样你就可以在 vendor.js 中存入未做修改的必要 library 或文件࿰…...

【python】基础知识点100问
以下是Python基础语法知识的30条要点整理,涵盖数据类型、函数、控制结构等核心内容,结合最新资料归纳总结: 基础30问 一、函数特性 函数多返回值 支持用逗号分隔返回多个值,自动打包为元组,接收时可解包到多个变量 def func(): return 1, "a" x, y = func()匿…...

uniapp 百家云直播插件打包失败
打包错误日志 Android自有证书 打包失败 错误日志: https://app.liuyingyong.cn/build/errorLog/cf41a610-effe-11ef-88db-05262d4c3e5d原因:需要导入插件依赖 依赖地址:https://ext.dcloud.net.cn/plugin?id16289 百家云直播插件地址 直播插…...

SpringBoot--springboot简述及快速入门
spring Boot是spring提供的一个子项目,用于快速构建spring应用程序 传统方式: 在众多子项目中,spring framework项目为核心子项目,提供了核心的功能,其他的子项目都需要依赖于spring framework,在我们实际…...

vscode_python远程调试_pathMappings配置说明
1.使用说明 vscode python 远程调试pathMappings 配置 launch.json "pathMappings": [{"localRoot": "本地代码目录","remoteRoot": "远程代码目录" # 注意不是运行目录, 是远程代码的目录}],2.测试验证 测试目的: 远程代…...

遨游5G-A防爆手机:赋能工业通信更快、更安全
在工业数字化转型与5G-A商用进程加速的双重驱动下,中国防爆手机市场正迎来历史性发展机遇。作为“危、急、特”场景通信解决方案服务商,遨游通讯深刻洞察到:当5G-A网络以超高速率、海量连接和毫秒级时延重塑行业生态时,防爆手机这…...

Profibus DP主站与Modbus RTU/TCP网关与海仕达变频器轻松实现数据交互
Profibus DP主站与Modbus RTU/TCP网关与海仕达变频器轻松实现数据交互 Profibus DP主站转Modbus RTU/TCP(XD-MDPBm20)网关在Profibus总线侧实现主站功能,在Modbus串口侧实现从站功能。可将ProfibusDP协议的设备(如:海…...

C++八股——智能指针
文章目录 1. 背景2. 原理与使用2.1 auto_ptr2.2 unique_ptr2.3 shared_ptr2.4 weak_ptr2.5 定制删除器 1. 背景 智能指针不是指针,是一个管理指针的类,用来存储指向动态分配对象的指针,负责自动释放动态分配的对象,防止堆内存泄漏…...

「华为」人形机器人赛道投资首秀!
温馨提示:运营团队2025年最新原创报告(共210页) —— 正文: 近日,【华为】完成具身智能赛道投资首秀,继续加码人形机器人赛道布局。 2025年3月31日,具身智能机器人头部创企【千寻智能&#x…...

格雷希尔G10和G15系列自动化快速密封连接器,适用于哪些管件的密封,以及它们相关的特性有哪些?
格雷希尔G10和G15系列快速密封连接器,用于自动化和半自动化过程中的外部或内部密封,通过使用气压驱动来挤压内部的密封圈,创造一个适用于各种管件的无泄漏密封连接,连接器内部的弹性密封圈可以提供其他产品不能提供的卓越密封性能…...

mac一键安装gpt-sovit教程中,homebrew卡住不动的问题
mac一键安装gpt-sovit教程 仅作为安装过程中解决homebrew卡住问题的记录 资源地址 https://www.yuque.com/baicaigongchang1145haoyuangong/ib3g1e/znoph9dtetg437xb#mlAoP 下载一键包 下载后并解压,找到install for mac.sh,终端执行bash空格拖拽in…...
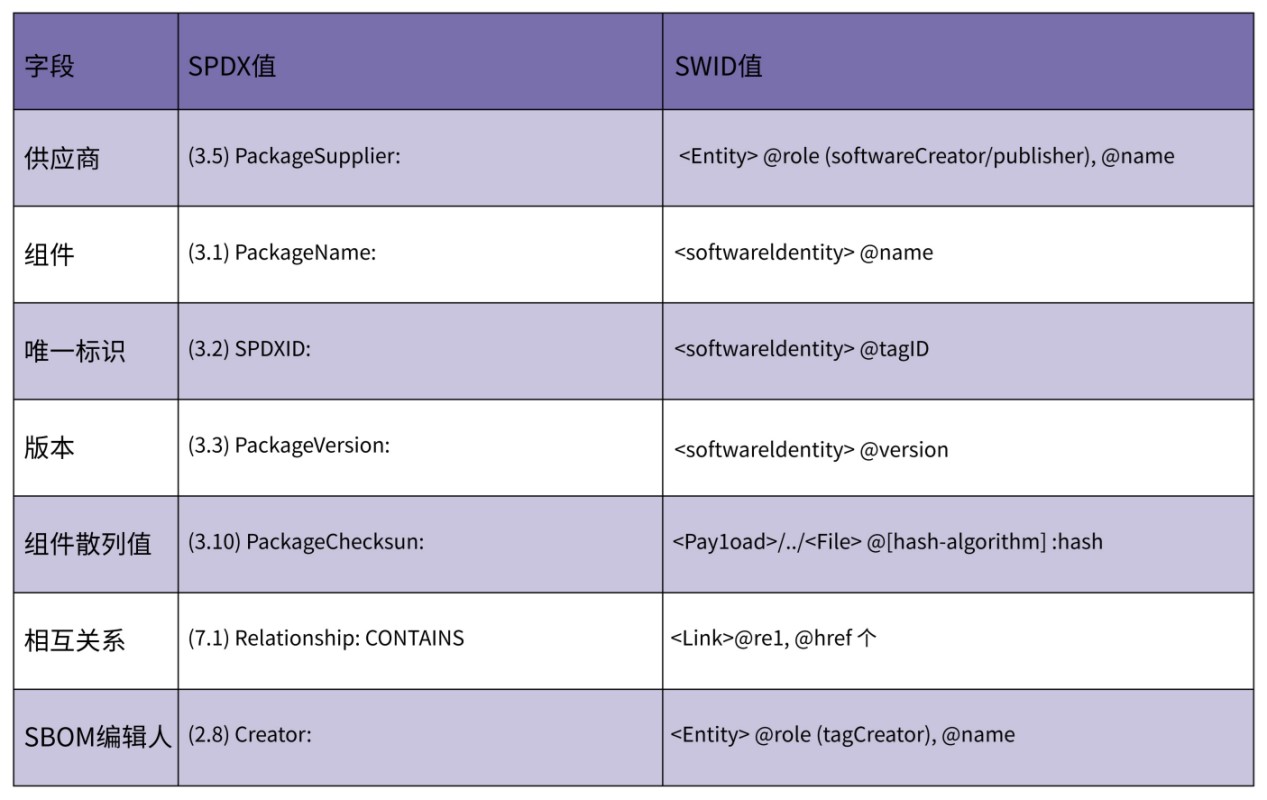
专栏特辑丨悬镜浅谈开源风险治理之SBOM与SCA
随着容器、微服务等新技术日新月异,开源软件成为业界主流形态,软件行业快速发展。但同时,软件供应链也越来越趋于复杂化和多样化,软件供应链安全风险不断加剧。 软件供应链安全主要包括软件开发生命周期和软件生存运营周期&#x…...

vue3项目创建-配置-elementPlus导入-路由自动导入
目录 方法一:create-vue 方法二 :Vite Vue Vite.config.ts配置 引入element-plus 安装 如何在项目中使用 Element Plus 完整引入 按需导入 vue3vite中自动配置路由的神器:vite-plugin-pages 1. 安装 2、修改vite.config.js中配置…...

MUSE Pi Pro 编译kernel内核及创建自动化脚本进行环境配置
视频讲解: MUSE Pi Pro 编译kernel内核及创建自动化脚本进行环境配置 今天分享的主题为创建自动化脚本编译MUSE Pi Pro的kernel内核,脚本已经上传到中 GitHub - LitchiCheng/MUSE-Pi-Pro-Learning: MUSE-Pi-Pro-Learning ,有需要可以自行clon…...

Java大师成长计划之第20天:Spring Framework基础
📢 友情提示: 本文由银河易创AI(https://ai.eaigx.com)平台gpt-4o-mini模型辅助创作完成,旨在提供灵感参考与技术分享,文中关键数据、代码与结论建议通过官方渠道验证。 在Java开发领域,Spring …...
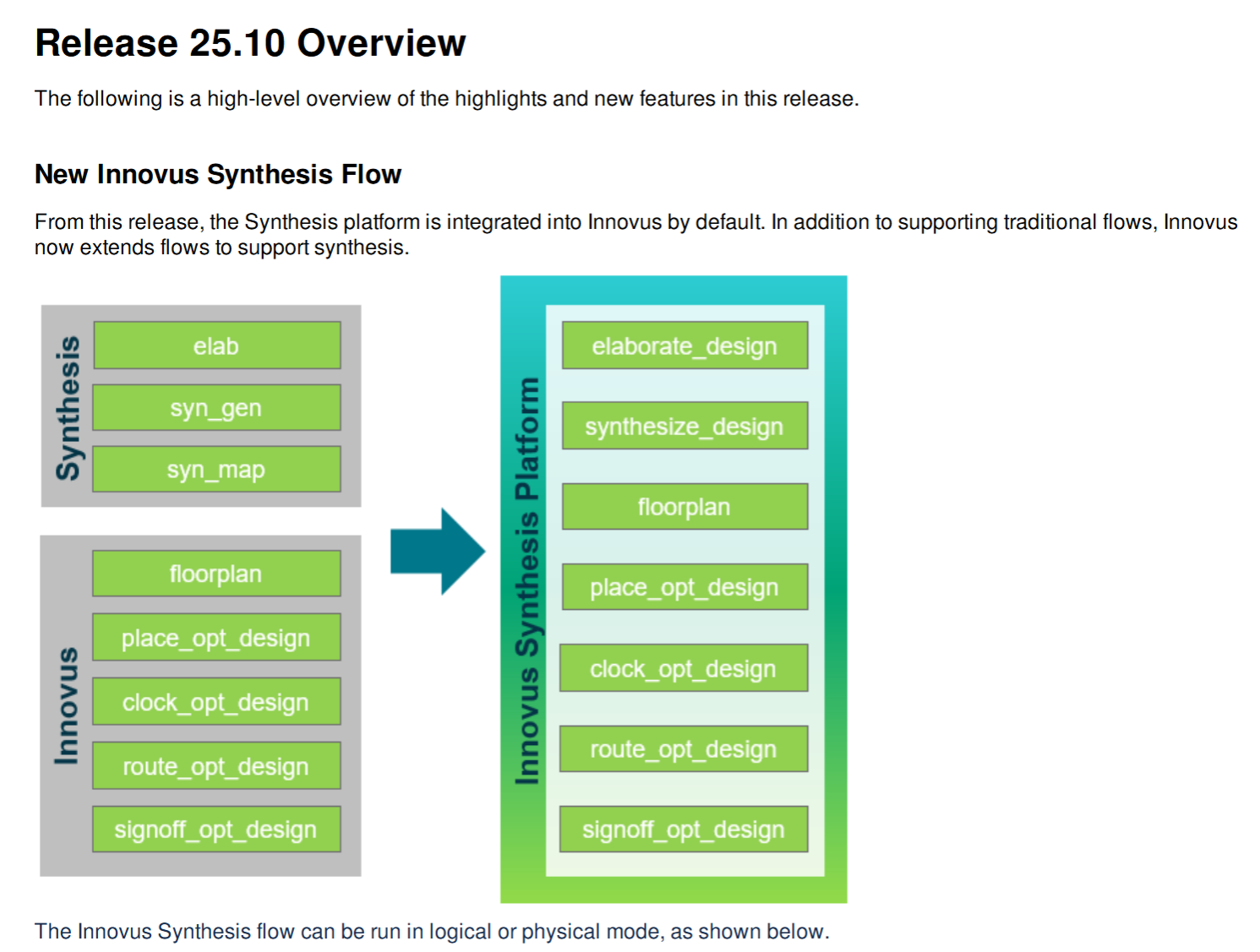
Innovus 25.1 版本更新:助力数字后端物理设计新飞跃
在数字后端物理设计领域,每一次工具的更新迭代都可能为项目带来巨大的效率提升与品质优化。今天,就让我们一同聚焦 Innovus 25.1 版本(即 25.10 版本)的更新要点,探寻其中蕴藏的创新能量。 一、核心功能的强势进 AI…...

FastAPI 和 MongoDB 实现请求头参数处理的示例,并在 React 中进行渲染
FastAPI 和 MongoDB 后端 安装必要的库 安装 FastAPI、Uvicorn、Motor(用于 MongoDB 的异步驱动)和 Pydantic(用于数据验证)。 pip install fastapi uvicorn motor pydantic创建 FastAPI 应用 创建一个文件 main.py,并…...

CodeBuddy 中国版 Cursor 实战:Redis+MySQL双引擎驱动〈王者荣耀〉战区排行榜
文章目录 一、引言二、系统架构设计2.1、整体架构概览2.2、数据库设计2.3、后端服务设计 三、实战:从零构建排行榜3.1、开发环境准备3.2、用户与战区 数据管理3.2.1、MySQL 数据库表创建3.2.2、实现用户和战区数据的 CURD 操作 3.3、实时分数更新3.4、排行榜查询3.5…...

码蹄集——分解、数组最大公约数、孪生质数、卡罗尔数、阶乘数
MT1158 分解 输入正整数N和M,判断N是否可以分解成M个不同的正整数的和,输出YES或者NO。 格式 输入格式:输入正整数N和M,空格分隔 输出格式:输出YES或者NO 样例 1 输入:5 2 输出:YES 思路…...

【React中函数组件和类组件区别】
在 React 中,函数组件和类组件是两种构建组件的方式,它们在多个方面存在区别,以下详细介绍: 1. 语法和定义 类组件:使用 ES6 的类(class)语法定义,继承自 React.Component。需要通过 this.props 来访问传递给组件的属性(props),并且通常要实现 render 方法返回 JSX…...

Idea Code Templates配置
Templates配置 配置位置模板案例 配置位置 Settings->Editor->File and Code Templates模板案例 #if (${PACKAGE_NAME} && ${PACKAGE_NAME} ! "")package ${PACKAGE_NAME};#endimport com.ktools.common.dataprocess.DataProcess; import com.ktools…...
