码蹄集——分解、数组最大公约数、孪生质数、卡罗尔数、阶乘数
MT1158 分解
输入正整数N和M,判断N是否可以分解成M个不同的正整数的和,输出YES或者NO。
格式
输入格式:输入正整数N和M,空格分隔
输出格式:输出YES或者NO
样例 1
输入:5 2
输出:YES
思路:从1~m遍历m个数,并相加,判断其与n的大小关系,只要小于n都满足条件
注意!!是不同的数
#include<bits/stdc++.h>using namespace std;int main()
{int n,m;cin>>n>>m;int sum=0;//m个不同的正整数能相加组成的最小正整数 for(int i=1;i<=m;i++)sum+=i;//只要比这个最小和要大都可以加一个数来实现要求//(加在任意一个由上面组成的序列中的数) if(n>=sum)cout<<"YES";elsecout<<"NO";return 0;} MT1162 数组最大公约数
给定一个由N个正整数组成的数组,求所有数组元素的最大公约数。
格式
输入格式:第一行输入数组长度N,第二行输入数组元素,整型,空格分隔。
输出格式:输出整型
样例 1
输入:
3 2 4 6
输出:2
思路:使用辗转相除法按两个两个求最大公约数
#include<bits/stdc++.h>using namespace std;int check(int a,int b)
{if(a<b){int tmp=a;a=b;b=tmp;}while(a&&b){int r=a%b;a=b;b=r;}return a;
}//不用判断a与b的大小的写法// int c;// while(a%b)// {// c=a%b;// a=b;b=c;// }int main()
{int n;cin>>n;int tmp1,tmp2;cin>>tmp1>>tmp2;int tmp=check(tmp1,tmp2);for(int i=1;i<n;i++){int tmp3;cin>>tmp3;tmp=check(tmp,tmp3);}cout<<tmp;return 0;} MT1163 孪生质数
在质数中,若两个质数之差为2,我们称之为孪生质数,例如(3、5)(5、7),输入2个正整数,判断他是不是孪生质数,输出YES或者NO。
格式
输入格式:输入整型
输出格式:输出YES或者NO
样例 1
输入:2 6
输出:NO
注意!!需要对1进行特判,1不是质数,但是check函数中1返回true
#include<bits/stdc++.h>using namespace std;bool check(int a)
{for(int i=2;i<a;i++)if(a%i==0)return false;return true;
}int main()
{int a,b;cin>>a>>b;//判断特殊情况,1不是质数,但是按照现在的1 3能输出yesif(a==1||b==1){cout<<"NO";return 0;}if(check(a)&&check(b)&&(abs(a-b)==2))cout<<"YES";elsecout<<"NO";return 0;} MT1165 卡罗尔数
卡罗尔数是其值满足4n–2(n+1)–1的整数(n为正整数)。输入正整数N判断它是不是卡罗尔数,输出YES或者NO。
格式
输入格式:输入正整数N
输出格式:输出YES或者NO
样例 1
输入:1
输出:YES
思路:直接遍历,因为num是从-1开始,刚开始时num一定小于n,所有结束条件是num>n
#include<bits/stdc++.h> using namespace std;bool check(int n)
{return 2*n-3;
}
int main( )
{int n;cin>>n;int num;for(int i=1;;i++){num=2*i-3;if(num==n){cout<<"YES";return 0; } else if(num>n){cout<<"NO";return 0;}}return 0;
}MT1167 自守数II
输入正整数N,检查该数是否为自守数输出YES或者NO。当且仅当一个数的平方以与该数相同的数字结尾时,该数称为自守数。
格式
输入格式:输入正整数N
输出格式:输出YES或者NO
样例 1
输入:76
输出:YES
自守数:一个数的平方的尾数等于该数自身的自然数
需要按位进行比较
#include<bits/stdc++.h> using namespace std;int main( )
{int n;cin>>n;int m=n*n;while(n&&m){if(m%10!=n%10){cout<<"NO";return 0;}m/=10;n/=10;}cout<<"YES";return 0;
}MT1168 阶乘数
输入正整数N,找出它是否是一个等于其他数的阶乘值的数,输出YES或者NO。
格式
输入格式:输入正整数N
输出格式:输出YES或者NO
样例 1
输入:5
输出:NO
思路:在循环中不断与该数阶乘进行对比
#include<bits/stdc++.h> using namespace std;int main( )
{int n;cin>>n;int sum=1;for(int i=1;i<=n;i++){sum*=i;if(n==sum){cout<<"YES";return 0;}}cout<<"NO";return 0;
}
相关文章:

码蹄集——分解、数组最大公约数、孪生质数、卡罗尔数、阶乘数
MT1158 分解 输入正整数N和M,判断N是否可以分解成M个不同的正整数的和,输出YES或者NO。 格式 输入格式:输入正整数N和M,空格分隔 输出格式:输出YES或者NO 样例 1 输入:5 2 输出:YES 思路…...

【React中函数组件和类组件区别】
在 React 中,函数组件和类组件是两种构建组件的方式,它们在多个方面存在区别,以下详细介绍: 1. 语法和定义 类组件:使用 ES6 的类(class)语法定义,继承自 React.Component。需要通过 this.props 来访问传递给组件的属性(props),并且通常要实现 render 方法返回 JSX…...

Idea Code Templates配置
Templates配置 配置位置模板案例 配置位置 Settings->Editor->File and Code Templates模板案例 #if (${PACKAGE_NAME} && ${PACKAGE_NAME} ! "")package ${PACKAGE_NAME};#endimport com.ktools.common.dataprocess.DataProcess; import com.ktools…...

在线SQL转ER图工具
在线SQL转ER图网站 在数据库设计、软件开发或学术研究中,ER图(实体-关系图) 是展示数据库结构的重要工具。然而,手动绘制ER图不仅耗时费力,还容易出错。今天,我将为大家推荐一款非常实用的在线工具——SQL…...

python高级特性
json.dumps({a:1,n:2}) #Python 字典类型转换为 JSON 对象。相当于jsonify data2 json.loads(json_str)#将 JSON 对象转换为 Python 字典 异步编程:在异步编程中,程序可以启动一个长时间运行的任务,然后继续执行其他任务,而无需等…...

汇编:子程序设计
一、 实验要求 实验目的: 熟练掌握算术运算汇编指令的使用熟练掌握子程序设计的基本方法熟练掌握程序的调试方法 实验内容: 编程实现两个数:#8888H和#79H的乘除运算结合实验1的代码,将加减乘除四则运算写成四个子程序ÿ…...

从概念表达到安全验证:智能驾驶功能迎来系统性规范
随着辅助驾驶事故频发,监管机制正在迅速补位。面对能力表达、使用责任、功能部署等方面的新要求,行业开始重估技术边界与验证能力,数字样机正成为企业合规落地的重要抓手。 2025年以来,围绕智能驾驶功能的争议不断升级。多起因辅…...

ubuntu 24.04 error: cannot uninstall blinker 1.7.0, record file not found. hint
最近在打python3.12的镜像,安装browser-gym的核心库,编译一个使用browswer agents的环境,然后出现了下面的问题: error: cannot uninstall blinker 1.7.0, record file not found. hint: the package was installed by debian.系…...

DeepSeek基于注意力模型的可控图像生成
DeepSeek大模型高性能核心技术与多模态融合开发 - 商品搜索 - 京东 图像的加噪与模型训练 在扩散模型的训练过程中,首先需要对输入的信号进行加噪处理,经典的加噪过程是在图像进行向量化处理后在其中添加正态分布,而正态分布的值也是与时间…...
“端 - 边 - 云”三级智能协同平台的理论建构与技术实现
摘要 随着低空经济与智能制造的深度融合,传统集中式云计算架构在实时性、隐私保护和资源效率上的瓶颈日益凸显。本文提出“端 - 边 - 云”三级智能协同平台架构,以“时空 - 资源 - 服务”三维协同理论为核心,构建覆盖终端感知、边缘计算、云端…...

AI时代,如何实现人机共舞?
在科技飞速发展的当下,人工智能(AI)已不再是科幻作品中的遥远想象,而是深入渗透到我们生活与工作的方方面面。从智能手机中的语音助手,到金融领域的风险预测模型;从医疗影像的智能诊断,到工业生…...

component :is是什么?
问: component :is是什么? 是组件? 那我们是不是就不需要自己创建组件了?还是什么意思?component :is和什么功能是类似的,同时和类似功能相比对什么时候用component :is…...

2025 3D工业相机选型及推荐
3D工业相机是专门为工业应用设计的三维视觉采集设备,能够获取物体的三维空间信息,在智能制造、质量检测、机器人引导等领域有广泛应用。 一、主要类型 1.结构光3D相机 通过投射特定光斑或条纹图案并分析变形来重建三维形状 典型代表:双目结构…...
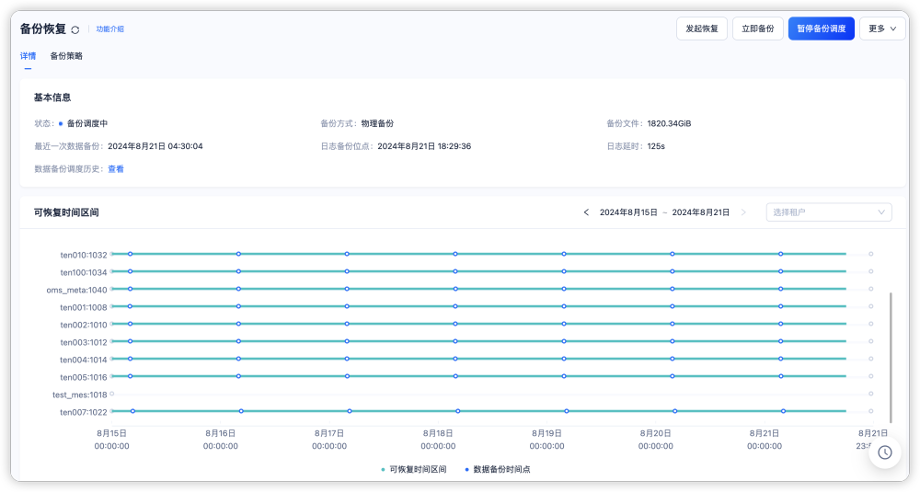
OceanBase 在业务监控系统中的应用实践
本文作者来自于一家总部在宁波的新能源上市公司,公司业务包括光伏新能源产品的研发与产销。 作为年产值达百亿的企业,监控系统是不可或缺的IT管理体系之一,对于确保业务连续性及预警风险非常重要。2022年,公司选择把Zabbix作为企业…...

每日Prompt:品牌化键盘键帽
提示词 一个超逼真的3D渲染图,展示了四个机械键盘键帽,排列成紧密的2x2网格,所有键帽相互接触。从等轴测角度观察。一个键帽是透明的,上面用红色印刷着“{just}”字样。另外三个键帽采用颜色:{黑色、紫色和白色}。一个…...

RabbitMQ发布订阅模式深度解析与实践指南
目录 RabbitMQ发布订阅模式深度解析与实践指南1. 发布订阅模式核心原理1.1 消息分发模型1.2 核心组件对比 2. 交换机类型详解2.1 交换机类型矩阵2.2 消息生命周期 3. 案例分析与实现案例1:基础广播消息系统案例2:分级日志处理系统案例3:分布式…...

超声波传感器模块
欢迎来到 破晓的历程的 博客 ⛺️不负时光,不负己✈️ 文章目录 1.HC-SR04介绍2.HC-SR04原理介绍2.1原理概述3.2原理详解 4驱动代码编写4.1写前思考4.2硬件连线 5.总结hcsr04.hhcsr04.c 1.HC-SR04介绍 超声波传感器有很多种类的型号:HC-SR04、UC-025、…...

LeetCode 513 找树左下角的值 LeetCode 112 路径总和 LeetCode106 从中序与后序遍历序列构造二叉树
LeetCode 513 找树左下角的值 迭代法——层序遍历 思路:对树进行层序遍历操作,层序遍历完后,输出树最后一层的第一个节点。 # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, val0, leftNone, r…...

Docker常见问题全攻略:从安装到优化
常见Docker安装问题及解决方案 系统兼容性问题排查安装过程中权限不足的解决方法网络配置问题导致安装失败的修复 系统兼容性问题排查 Docker在安装过程中可能会遇到系统兼容性问题,尤其是在较旧的操作系统或特定硬件架构上。确保操作系统版本符合Docker的最低要…...

『大模型笔记』Langchain作者Harrison Chase专访:环境智能体与全新智能体收件箱
Langchain作者Harrison Chase专访:环境智能体与全新智能体收件箱 文章目录 摘要访谈内容什么环境智能体为什么要探索环境智能体怎么让人类能更方便地和环境智能体互动参考文献摘要 LangChain 的 CEO Harrison Chase 提出了_“环境智能体”(Ambient Agents)的概念,这是一种…...

Kafka集群加入新Broker节点会发生什么
Kafka集群加入新Broker节点会发生什么 当向现有的Kafka集群添加新的Broker节点时,会触发一系列自动和手动的过程。以下是详细的流程和影响: 自动发生的流程 集群发现与注册 新Broker启动时会向ZooKeeper注册自己加入集群的/brokers/ids路径下其他Broke…...

SpringBoot的外部化配置
一、什么是外部化配置 外部化配置是指把应用程序中各种可配置的参数、属性等信息,从代码内部提取出来,放置在外部的配置文件、数据库或配置中心等地方(比如使用.properties、.yml 或.xml 等格式的文件)进行管理。提高应用程序的可…...

3.5 统计初步
本章系统阐述统计推断理论基础,涵盖大数定律、抽样分布、参数估计与假设检验等核心内容。以下从六个核心考点系统梳理知识体系: 考点一:大数定律与中心极限定理 1. 大数定律 切比雪夫不等式: 设随机变量 X X X 的数学期望 E (…...

数字IC后端实现教程 | Early Clock Flow和Useful skew完全不是一个东西
数字后端零基础入门系列 | Innovus零基础LAB学习Day10 Q: Early clock flow和useful skew都是做短某段路径,这两个有什么区别呢,既然这样还用useful skew是不是有点多余了? Useful Skew技术 在不使用useful skew技术,第一级FF到第二级FF的…...
)
.Net HttpClient 管理客户端(初始化与生命周期管理)
HttpClient 初始化与生命周期管理 HttpClient 旨在实例化一次,并在应用程序的整个生命周期内重复使用。 为实现复用,HttpClient类库默认使用连接池和请求管道,可以手动管理(连接池、配置管道、使用Polly); 结合IoC容器、工厂模式(提供了IHt…...

【Docker】Docker环境下快速部署Ollama与Open-WebUI:详细指南
Docker环境下快速部署Ollama与Open-WebUI:详细指南 在本篇文章中,我们将深入探讨如何在Docker中高效部署 Ollama 和 Open-WebUI,并解决在实际使用中常见的问题,确保你的模型服务稳定高效地运行。 一、Ollama 和 Open-WebUI 快速部…...

MySQL OCP试题解析(3)
试题如图所示: 一、解析 正确选项:D)The backup can be impacted when DDL operations run during the backup(备份期间运行的 DDL 操作可能影响备份) 1. 关键知识点解析: 题目中的命令 mysqlbackup 使用了…...

SpringCloud之Gateway基础认识-服务网关
0、Gateway基本知识 Gateway 是在 Spring 生态系统之上构建的 API 网关服务,基于 Spring ,Spring Boot 和 Project Reactor 等技术。 Gateway 旨在提供一种简单而有效的方式来对 API 进行路由,以及提供一些强大的过滤器功能,例如…...

ubuntu----100,常用命令2
目录 文件与目录管理系统信息与管理用户与权限管理网络配置与管理软件包管理打包与压缩系统服务与任务调度硬件信息查看系统操作高级工具开发相关其他实用命令 在 Ubuntu 系统中,掌握常用命令可以大幅提升操作效率。以下是一些常用的命令,涵盖了文件管理…...
CMOS VLSI Design)
数字ic后端设计从入门到精通4(含fusion compiler, tcl教学)CMOS VLSI Design
Layout Design Rules 一、什么是 Layout Design Rules? 布局设计规则是一套用于指导芯片物理设计的几何约束条件,确保设计可以在特定制造工艺下被正确制造。这些规则通常由代工厂(foundry)提供,规定了最小线宽、间距、…...
