【递归、搜索和回溯】二叉树中的深搜
个人主页 : zxctscl
专栏 【C++】、 【C语言】、 【Linux】、 【数据结构】、 【算法】
如有转载请先通知
文章目录
- 前言
- 1 2331. 计算布尔二叉树的值
- 1.1 分析
- 1.2 代码
- 2 129. 求根节点到叶节点数字之和
- 2.1 分析
- 2.2 代码
- 3 814. 二叉树剪枝
- 3.1 分析
- 3.2 代码
- 4 98. 验证二叉搜索树
- 4.1 分析
- 4.2 代码
- 5 230. 二叉搜索树中第 K 小的元素
- 5.1 分析
- 5.2 代码
- 6 257. 二叉树的所有路径
- 6.1 分析
- 6.2 代码
前言
上一篇提到递归、搜索和回溯介绍: 【递归、搜索和回溯】递归、搜索和回溯介绍及递归类算法例题,继续来看着类型的题目
1 2331. 计算布尔二叉树的值

1.1 分析
看一下例一:把数字按题目换算成符号就是图片右边这样的情况,false&true=false,true|false=true。最后结果结果就是true。

算法原理:递归(dfs)
重复子问题:
主问题就是这棵树是true还是false,左子树是true还是false,把左子树传过去;右子树是true还是false,把右子树传过去。函数头bool dfs(root)
函数体:bool left=dfs(root->left);bool right=dfs(root->right);再把左右子树按规则计算
出口:遇到叶子节点就返回结果
1.2 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left==nullptr)return root->val==0?false:true;bool left=evaluateTree(root->left);bool right=evaluateTree(root->right);return root->val==2?left|right:left&right;}
};
2 129. 求根节点到叶节点数字之和

2.1 分析
算法:递归
函数头:
传一个节点,计算与它相连的所有叶子结点的和
int dfs(root,presum)
函数体:计算节点5的值,那么第一步就得拿到到5时前面的值,也就是125,第二步,拿到它左子树值1258,第三步拿到它右子树的值12594+125931=138525,第四步,将左右两边相加1258+138525

递归出口:叶子结点
2.2 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumNumbers(TreeNode* root) {return dfs(root,0);}int dfs(TreeNode* root,int presum){presum=presum*10+root->val;if(root->left==nullptr&&root->right==nullptr)return presum;int ret=0;if(root->left)ret+=dfs(root->left,presum);if(root->right)ret+=dfs(root->right,presum);return ret;}
};
3 814. 二叉树剪枝

3.1 分析
里面所有包含0的子树全部剪掉
算法原理:递归
通过决策树,抽象出递归的三个核心问题
遇到0的时候,要先判断它的左子树和右子树是否是0,就要用到后序遍历。
当后序遍历节点的左子树遇到0后用null返回,如果左子树没有改变,就直接返回它的值。

函数头 Node* dfs(root)
函数体
(1)处理左子树
(2)处理右子树
(3)判断
递归出口
当root为空就返回
3.2 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root==nullptr)return nullptr;root->left=pruneTree(root->left);root->right=pruneTree(root->right);if(root->left==nullptr&&root->right==nullptr&&root->val==0){root=nullptr;}return root;}
};
4 98. 验证二叉搜索树

4.1 分析
二叉搜索树的中序遍历的结果,是一个有序的序列用这个性质来做这道题。
用一个全局变量prev,让这个全局变量先初始化为负无穷大,当在进行中序遍历的时候,到一个节点的时候,prev记录它的前面遍历节点的值,拿prev和当前节点的值比较后,更新prev的值,继续遍历,是有序的就继续遍历,更新。
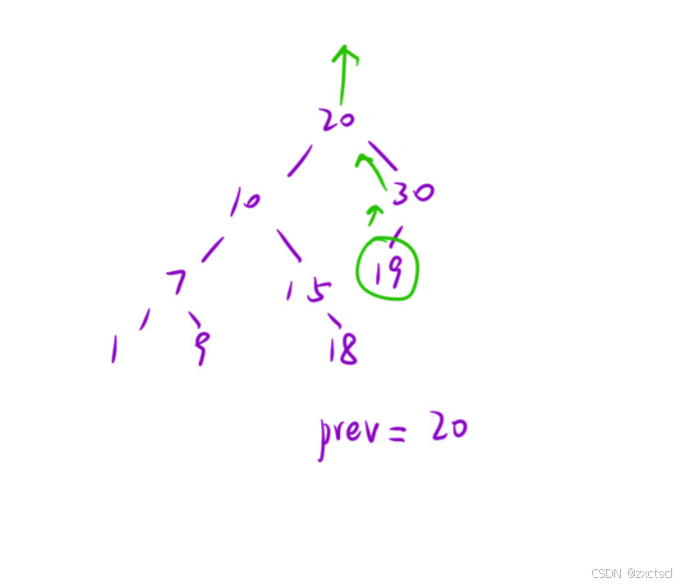
算法:递归
策略一:
左子树是二叉搜索树
当前节点符合二叉搜索树
右节点是二叉搜索树
策略二:剪枝
当全局变量prev,遍历到19的时候就已经不是二叉搜索树了,就不需要再往下遍历了。

4.2 代码
策略一:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{long prev=LONG_MIN;
public:bool isValidBST(TreeNode* root) {if(root==nullptr)return true;bool left=isValidBST(root->left);bool cur=false;if(root->val>prev){cur=true; }prev=root->val;bool right=isValidBST(root->right);return left&&right&&cur;}};
策略二:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{long prev=LONG_MIN;
public:bool isValidBST(TreeNode* root) {if(root==nullptr)return true;bool left=isValidBST(root->left);if(left==false)return false;bool cur=false;if(root->val>prev){cur=true; }prev=root->val;bool right=isValidBST(root->right);return left&&right&&cur;}};
5 230. 二叉搜索树中第 K 小的元素

5.1 分析
二叉搜索树的中序遍历的结果,是一个有序的序列用这个性质来做这道题。
与上面那题类似。
这题用两个全局变量和中序遍历。
一个全局变量c用来计数,另一个ret用来记录遍历节点对应的值。
每遍历一次c就减减,当c等于0时候的ret值就是最终需要的值。
当找到最终结果时候,此时c=0后面就不用遍历了。

5.2 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {int count;int ret;
public:int kthSmallest(TreeNode* root, int k) {count=k;dfs(root);return ret; }void dfs(TreeNode* root){if(root==nullptr||count==0)return;dfs(root->left);count--;if(count==0)ret=root->val;dfs(root->right);}
};
6 257. 二叉树的所有路径

6.1 分析
全局变量
回溯->恢复现场
一道题出现了回溯才能想到恢复现场。
题目要求以箭头形式返回结果
算法原理:
根节点开始向下搜索,遇到一个叶子结点,存一下这个路径,存到数组中返回。
用两个全局变量,一个string[] ret表示字符串数组保存最终结果,遇到一个叶子结点路径就放进去。另一个string path用来记录路径,遇到不是叶子结点就在后面加上这个值,遇到叶子结点后,把这个path加到ret里面。
但要考虑path的回溯问题:
为了防止回溯多加上叶子结点的值,就得恢复现场,再回溯时候就得剪掉上一个路径的叶子结点。
全局变量恢复现场不容易,就不用全局的string path。

如果把path设置成函数头参数,就不用恢复现场,函数的特性就会帮助恢复现场。
函数头:
void dfs(root,path)
当遍历时候,就会重新创建一个path,而上面的path也在:

函数体
当遇到叶子结点时:就把path加到ret里面
不是叶子结点就继续遍历
递归出口:
当左子树为空的时候,就不需要遍历它左子树,把它左子树就剪掉。

不想剪枝,就直接root为空返回
6.2 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> ret;vector<string> binaryTreePaths(TreeNode* root) {string path;if(root==nullptr)return ret;dfs(root,path);return ret;}void dfs(TreeNode* root,string path){path+=to_string(root->val);if(root->left==nullptr&&root->right==nullptr){ret.push_back(path);return;}path+="->";if(root->left)dfs(root->left,path);if(root->right)dfs(root->right,path);}
};
有问题请指出,大家一起进步!!!
相关文章:

【递归、搜索和回溯】二叉树中的深搜
个人主页 : zxctscl 专栏 【C】、 【C语言】、 【Linux】、 【数据结构】、 【算法】 如有转载请先通知 文章目录 前言1 2331. 计算布尔二叉树的值1.1 分析1.2 代码 2 129. 求根节点到叶节点数字之和2.1 分析2.2 代码 3 814. 二叉树剪枝3.1 分析3.2 代码 4 98. 验证…...

Algolia - Docsearch的申请配置安装【以踩坑解决版】
👨🎓博主简介 🏅CSDN博客专家 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入!…...

Linux513 rsync本地传输 跨设备传输 一
ping节点bPing通 仅主机模式不需要设置网关节点a也可以Ping通节点b 同步成功 下载文件夹成功 今日源码 节点a 节点b...

leetcode 383. Ransom Note
题目描述 代码 class Solution { public:bool canConstruct(string ransomNote, string magazine) {vector<int> table(26,0);for(char ch : magazine){table[ch-a];}for(char ch : ransomNote){table[ch-a]--;if(table[ch-a] < 0)return false;}return true;} };...

Skyvern:用 AI+视觉驱动浏览器自动化
Skyvern:用 AI视觉驱动浏览器自动化 一、前言二、项目概览2.1 Skyvern 项目简介2.2 代码结构与模块划分 三、环境搭建与快速上手3.1 环境准备3.1.1 系统与依赖3.1.2 克隆项目3.1.3 安装 Python 依赖3.1.4 配置环境变量3.1.5 启动服务 3.2 验证安装 四、核心功能与实…...

数据库原理期末考试速成--最后附带两套题
引言 为什么从3开始呢,毕竟是速成吗,总要放弃一些东西 前两章1.概论 2.关系数据库:这里面都是一些运算符什么的,我感觉都学这个:笛卡尔积之列的都会算 这两章比较重要的我就放在这里了 选择、投影、连接、除、并、交、差,其中选择、投影、并、差、笛卡尔积是5种基本关…...

《探索React Native社交应用中WebRTC实现低延迟音视频通话的奥秘》
WebRTC,全称为Web Real-Time Communication,是一项开创性的开源技术,为Web和移动应用开启了实时通信的大门。它打破了传统通信的束缚,使得应用之间无需依赖繁琐的中间服务器,就能实现直接的点对点通信,这是…...

关于vue 本地代理
接口调用:其中我们可以约定一个拦截的标识, 用来给本地 http://localhost/ 进行代理要请求的测试地址https:abc.com 例子: axios.post(/OwnRateReport/-------------------------------------------------------00001)devServer: {proxy: {/…...

#跟着若城学鸿蒙#HarmonyOS NEXT学习之Blank组件详解
一、组件介绍 Blank(空白)组件是HarmonyOS NEXT中一个简单但非常实用的UI组件,它主要用于在布局中创建空白区域,帮助开发者更灵活地控制界面元素之间的间距和布局结构。虽然Blank组件本身不显示任何内容,但它在界面设…...
通过自定义 MAVLink 消息与 QGroundControl (QGC) 通信)
PX4开始之旅(二)通过自定义 MAVLink 消息与 QGroundControl (QGC) 通信
核心知识点:通过自定义 MAVLink 消息与 QGroundControl (QGC) 通信 1. 通俗易懂的解释 想象一下,MAVLink 就像是无人机(飞控)和地面站(QGroundControl)之间约定好的一种“语言”。这种语言有很多标准的“…...

数据结构基础--蓝桥杯备考
1.优缺点总述 STL中各容器对比图 各类线性数据结构优缺点 1.数组 1.优点 1.简单,容易理解 2.访问快捷,只需要用下标就可以 3.有某些应用场景直接对应,例如二维数组对应平面 2.缺点 删除和插入数据非常耗时 2.链表 1.优点 插入和删…...

2.4GHz无线通信芯片选型指南:集成SOC与低功耗方案解析
今天给大家分享几款2.4GHz无线通信芯片方案: 一、集成SOC芯片方案 XL2407P(芯岭技术) 集成射频收发机和微控制器(如九齐NY8A054E) 支持一对多组网和自动重传 发射功率8dBm,接收灵敏度-96.5dBm(…...

安卓刷机模式详解:Fastboot、Fastbootd、9008与MTK深刷
安卓刷机模式详解:Fastboot、Fastbootd、9008与MTK深刷 一、刷机模式对比 1. Fastboot模式 简介:传统安卓底层刷机模式,通过USB连接电脑操作优点:支持大多数安卓设备,操作相对简单缺点:需要设备进入特定…...
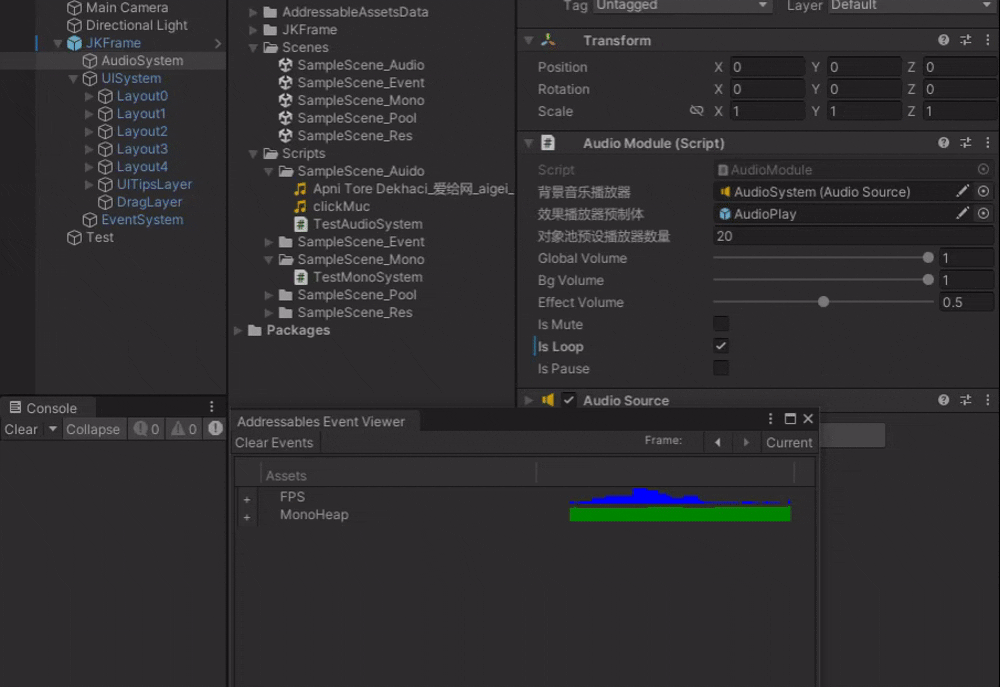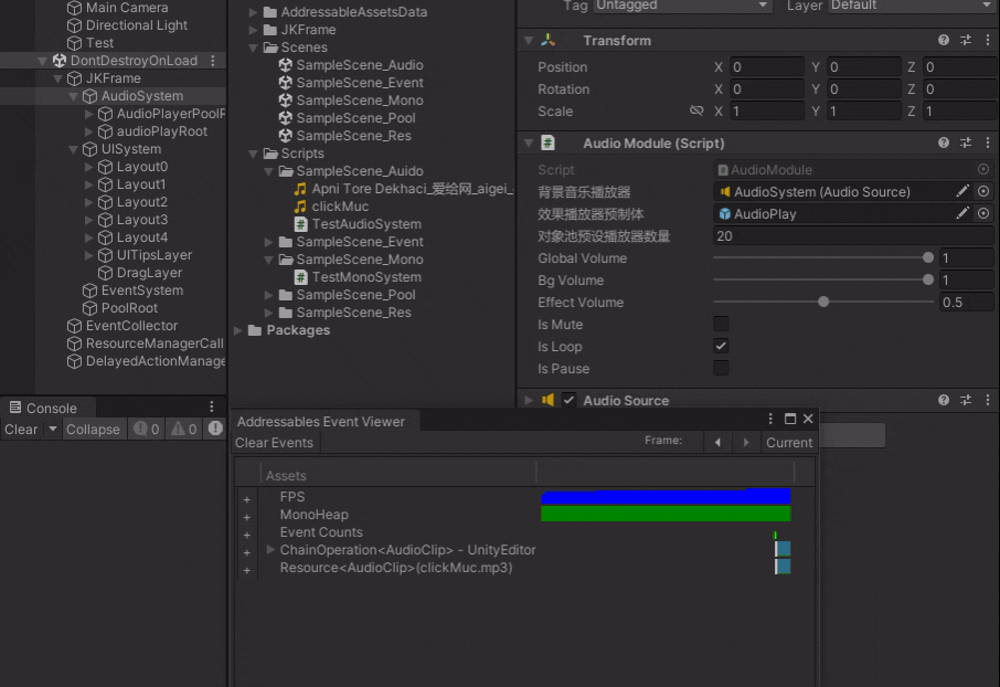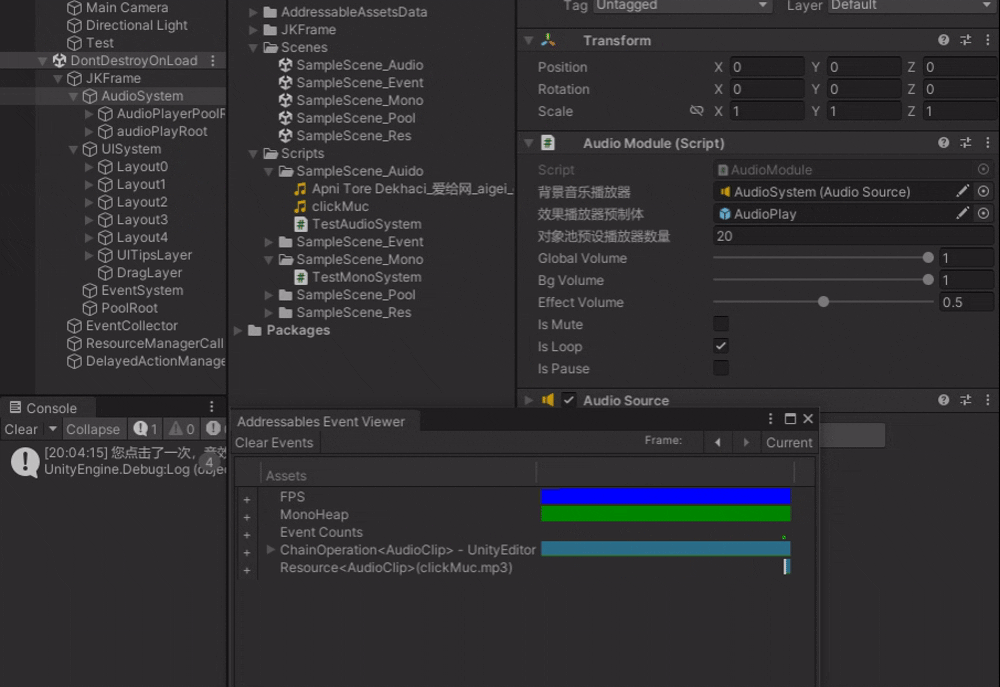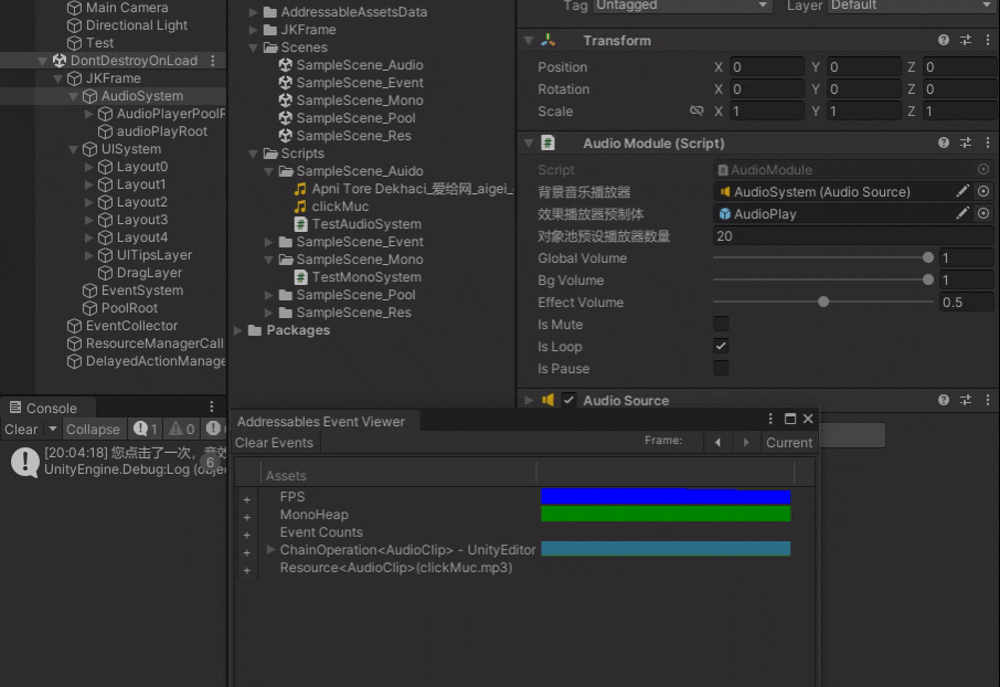
Unity_JK框架【5】音效系统实现
在游戏开发中,音频是不可或缺的一部分,它能够极大地增强游戏的沉浸感和趣味性。今天,我们就用JK框架 探讨一下如何在Unity中实现一个强大的音频系统,并且通过实际的测试脚本来验证其功能👏。 一、音频模块类࿱…...

鸿蒙 从打开一个新窗口到Stage模型的UIAbility组件
打开一个新的窗口 我们首先来实现如何在一个应用中打开一个新窗口,使用的模型是 Stage 模型 在项目文件里,新建一个 newWindow.ets 新文件 src/main/ets/pages/newWindow.ets newWindow.ets文件里面随便写点什么都行,这里是第一步创建的文件…...

MySQL数据库——视图
目录 一、视图是什么? 二、特点 三、创建视图 四.查询视图 五.更新视图 六.视图的作用 总结 一、视图是什么? 视图是从一个或多个表中导出的虚拟表,它本身不存储数据,而是基于 SQL 查询的结果集。 二、特点 1.虚拟性࿱…...
)
redis数据结构-09 (ZADD、ZRANGE、ZRANK)
Redis 排序集简介:ZADD、ZRANGE、ZRANK Redis 有序集合是一种功能强大的数据结构,兼具集合和哈希的特性。它维护一组唯一元素,类似于集合;但每个元素都与一个分数相关联,类似于哈希。分数用于对有序集合中的元素进行排…...

PyTorch API 1 - 概述、数学运算、nn、实用工具、函数、张量
文章目录 torch张量创建操作索引、切片、连接与变异操作 加速器生成器随机采样原地随机采样准随机采样 序列化并行计算局部禁用梯度计算数学运算常量逐点运算归约操作比较运算频谱操作其他操作BLAS 和 LAPACK 运算遍历操作遍历操作遍历操作遍历操作遍历操作遍历操作遍历操作遍历…...
长短期记忆网络(LSTM)深度解析:理论、技术与应用全景
长短期记忆网络(LSTM)作为循环神经网络(RNN)的重要变体,通过门控机制有效解决了传统RNN的梯度消失问题,成为时序数据处理的核心技术。本文从理论起源、数学建模、网络架构、工程实现到行业应用,…...

c语言第一个小游戏:贪吃蛇小游戏02
接上文继续学习 ncurse的上下左右键获取 想要使用ncurse的功能键,也就是键盘快捷键,不是q、r、t,是 上下左右、F1、F2等等的键,我们叫做功能键要是想用这些功能键需要使用keypad函数 Keypad(stdscr,1); 从stdscr接收标准中&…...
!!!学会Python爬虫轻松赚外快】)
【Python爬虫 !!!!!!政府招投标数据爬虫项目--医疗实例项目文档(提供源码!!!)!!!学会Python爬虫轻松赚外快】
政府招投标数据爬虫项目--医疗实例项目文档 1. 项目概述1.1 项目目标1.2 技术栈 2. 系统架构2.1 模块划分2.2 流程示意图 3. 核心模块设计3.1 反爬处理模块(utils/anti_crawler.py)3.1.1 功能特性3.1.2 关键代码 3.2 爬虫模块(crawler/spider…...

Android架构之自定义native进程
在Android五层架构中,native层基本上全是c的世界,这些c进程基本上靠android世界的第一个进程init进程创建,init通过rc配置文件,创建了众多的c子进程,也是这众多的c进程,构建了整个android世界的native层。 …...

talk-centos6之间实现
在 CentOS 6.4 上配置和使用 talk 工具,需要注意系统版本较老,很多配置可能不同于现代系统。我会提供 详细步骤 自动化脚本,帮你在两台 CentOS 6.4 机器上实现局域网聊天。 ⸻ 🧱 一、系统准备 假设你有两台主机: …...

《100天精通Python——基础篇 2025 第18天:正则表达式入门实战,解锁字符串处理的魔法力量》
目录 一、认识正则表达式二、正则表达式基本语法2.1 行界定符2.2 单词定界符2.3 字符类2.4 选择符2.5 范围符2.6 排除符2.7 限定符2.8 任意字符2.9 转义字符2.10 反斜杠2.11 小括号2.11.1 定义独立单元2.11.2 分组 2.12 反向引用2.13 特殊构造2.14 匹配模式 三、re模块3.1 comp…...

数组中元素如何交换与打乱
1 问题 在本周学习了java基础语法中的数组,在学习数组后,我们会遇到关于数组中元素的倒序,交换,和无序打乱等问题,在Python中我们可以用list的方法进行元素倒序,那么我们在java中应该如何实现数组用元素的倒序和元素的打乱呢? 2 方法 使用循环,Random类,下标索引实现 关于元素…...

Nuitka 已不再安全? Nuitka/Cython 打包应用逆向工具 -- pymodhook
pymodhook是一个记录任意对Python模块的调用的库,用于Python逆向分析。 pymodhook库类似于Android的xposed框架,但不仅能记录函数的调用参数和返回值,还能记录模块的类的任意方法调用,以及任意派生对象的访问,基于pyob…...

【C】初阶数据结构14 -- 归并排序
本篇文章主要是讲解经典的排序算法 -- 归并排序 目录 1 递归版本的归并排序 1) 算法思想 2) 代码 3) 时间复杂度与空间复杂度分析 (1) 时间复杂度 (2) 空间复杂度 2 迭代版本的归并…...
华为网路设备学习-21 IGP路由专题-路由过滤(filter-policy)
一、路由过滤(filter-policy) 1、用于控制路由更新、接收的一个工具 2、只能过滤路由信息,无法过滤LSA 二、路由过滤(filter-policy)与动态路由协议 1、距离矢量路由协议 RIP动态路由协议 交换的是路由表࿰…...

NestJS 框架深度解析
框架功能分析 NestJS 是一个基于 Node.js 的渐进式框架,专为构建高效、可扩展的服务器端应用程序而设计。其核心理念结合了 面向对象编程(OOP)、函数式编程(FP) 和 函数式响应式编程(FRP)&…...

人脸识别门禁系统技术文档
人脸识别门禁系统技术文档 序言 本文档详细描述了人脸识别门禁系统的技术实现原理与方法。该系统旨在提供高安全性的门禁管理解决方案,通过先进的人脸识别技术,实现无接触式身份验证,提高安全管理效率。 系统整合了人工智能与计算机视觉技…...
