最优化方法Python计算:有约束优化应用——线性可分问题支持向量机
设问题的数据样本点 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi,yi), x i ∈ R n \boldsymbol{x}_i\in\text{R}^n xi∈Rn, y i = ± 1 y_i=\pm1 yi=±1, i = 1 , 2 , ⋯ , m i=1,2,\cdots,m i=1,2,⋯,m。由于标签数据 y i ∈ { − 1 , 1 } y_i\in\{-1,1\} yi∈{−1,1},故形成一个2-分类问题。假定特征数据 { x i } \{\boldsymbol{x}_i\} {xi}在欧氏空间 R n \text{R}^n Rn中按对应标签数据 y i y_i yi的取值(-1或1)分成两个簇,如下图所示。

我们希望在两个样本点簇之间找到一个超平面 π \pi π( n = 2 n=2 n=2时为一条直线, n = 3 n=3 n=3是为一平面): w 1 x 1 + w 2 x 2 + ⋯ + w n x n + w n + 1 = 0 w_1x_1+w_2x_2+\cdots+w_nx_n+w_{n+1}=0 w1x1+w2x2+⋯+wnxn+wn+1=0——称为分离面——将它们分开。即若 y i = 1 y_i=1 yi=1,则 w 1 x i 1 + w 2 x i 2 + ⋯ + w n x i n + w n + 1 > 0 w_1x_{i_1}+w_2x_{i_2}+\cdots+w_nx_{i_n}+w_{n+1}>0 w1xi1+w2xi2+⋯+wnxin+wn+1>0。否则, w 1 x i 1 + w 2 x i 2 + ⋯ + w n x i n + w n + 1 < 0 w_1x_{i_1}+w_2x_{i_2}+\cdots+w_nx_{i_n}+w_{n+1}<0 w1xi1+w2xi2+⋯+wnxin+wn+1<0。若2-分类问题存在分离面,称其为线性可分的。此时,分离面往往并不唯一(见上图),希望算得最优者:每个样本点与分离面尽可能远,这样的分离面称为线性可分问题的决策面(上图中黑色的那一条)。
理论推导可得线性可分问题的决策面的系数和截距 w 0 = ( w 0 1 ⋮ w 0 n w 0 n + 1 ) \boldsymbol{w}_0=\begin{pmatrix}w_{0_1}\\\vdots\\w_{0_n}\\w_{0_{n+1}}\end{pmatrix} w0= w01⋮w0nw0n+1 是二次规划
{ min 1 2 w ⊤ H w s.t. y i ( x i ⊤ , 1 ) w ≥ 1 i = 1 , 2 , ⋯ , m \begin{cases} \min\quad\frac{1}{2}\boldsymbol{w}^\top\boldsymbol{Hw}\\ \text{s.t.}\quad\quad y_i(\boldsymbol{x}_i^\top,1)\boldsymbol{w}\geq1\quad i=1,2,\cdots,m \end{cases} {min21w⊤Hws.t.yi(xi⊤,1)w≥1i=1,2,⋯,m
的最优解。其中, H = ( 1 0 ⋯ 0 0 0 1 ⋯ 0 0 ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 ⋯ 1 0 0 0 ⋯ 0 0 ) \boldsymbol{H}=\begin{pmatrix}1&0&\cdots&0&0\\0&1&\cdots&0&0\\\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&\cdots&1&0\\0&0&\cdots&0&0\end{pmatrix} H= 10⋮0001⋮00⋯⋯⋱⋯⋯00⋮1000⋮00 。注意, H \boldsymbol{H} H半正定且 1 2 w ⊤ H w = 1 2 ∑ i = 1 n w i 2 \frac{1}{2}\boldsymbol{w}^\top\boldsymbol{Hw}=\frac{1}{2}\sum\limits_{i=1}^nw_i^2 21w⊤Hw=21i=1∑nwi2。
样本点中,满足 y i ( x i ⊤ , 1 ) w 0 = 1 y_i(\boldsymbol{x}_i^\top,1)\boldsymbol{w}_0=1 yi(xi⊤,1)w0=1的 x i \boldsymbol{x}_i xi,称为支持向量。下图展示了2维空间中线性可分问题的决策线及支持向量的实例。图中通过支持向量且平行于决策线 ( x ⊤ , 1 ) w 0 = 0 (\boldsymbol{x}^\top,1)\boldsymbol{w}_0=0 (x⊤,1)w0=0(黑色)的直线 ( x ⊤ , 1 ) w 0 = ± 1 (\boldsymbol{x}^\top,1)\boldsymbol{w}_0=\pm1 (x⊤,1)w0=±1(灰色),称为支持向量机的硬边界。不难理解,决策平面是由支持向量决定,这也是支持向量机模型名称的由来。

一旦通过训练支持向量机模型算得决策平面 π \pi π: ( x ⊤ , 1 ) w 0 = 0 (\boldsymbol{x}^\top,1)\boldsymbol{w}_0=0 (x⊤,1)w0=0。对新的样本特征数据 x \boldsymbol{x} x,计算
y = ( x ⊤ , 1 ) w 0 y=(\boldsymbol{x}^\top,1)\boldsymbol{w}_0 y=(x⊤,1)w0
若 y > 0 y>0 y>0,预测 x \boldsymbol{x} x属于类别“1”。否则,属于类别“-1”。即以
sign ( ( x ⊤ , 1 ) w 0 ) . \text{sign}((\boldsymbol{x}^\top,1)\boldsymbol{w}_0). sign((x⊤,1)w0).
作为分类预测值。其中,符号函数
sign ( x ) = { 1 x > 0 0 x = 0 − 1 x < 0 . \text{sign}(x)=\begin{cases} 1&x>0\\ 0&x=0\\ -1&x<0 \end{cases}. sign(x)=⎩ ⎨ ⎧10−1x>0x=0x<0.
虽然支持向量机的作为分类器与线性回归分类器所求目标都是一个线性函数但求解机制不同,前者用决策面来分隔样本点,后者用超平面来拟合样本点。这种不同的求解机制体现在需要求解的优化问题类型的区别。下列代码实现线性可分问题的支持向量机模型。
import numpy as np #导入numpy
from scipy.optimize import minimize #导入minimize等
class LineSvmModel(LineModel): #线性支持向量机模型def obj(self, w): #目标函数return 0.5 * (np.dot(w[:(self.p - 1)], w[:(self.p - 1)]))def fit(self, X, Y, w = None): #训练函数print("训练中...,稍候")m = X.shape[0]self.scalar = (len(X.shape) == 1) #是否1-维样本self.A, self.y = self.pretreat(X, Y) #数据预处理self.p = self.w0len() #模型参数长度if not isinstance(w, np.ndarray):if w == None:w = np.random.random(self.p)else:w = np.array([w] * self.p)g = lambda x: self.y.reshape(m, 1) * self.A @ x - 1.0cons = {'type': 'ineq', 'fun': g} #不等式约束res = minimize(self.obj, w, constraints = cons) #计算优化模型参数self.w0 = res.xself.coef_, self.intercept_ = self.coef_inte() #计算超平面系数和截距self.support_ = np.where(np.abs(Y.reshape(m, 1) * self.A\ #支持向量下标集@ self.w0.reshape(self.p, 1) - 1.0) < 1e-6)[0]print("%d次迭代后完成训练。"%res.nit)def ynormalize(self, y, trained): #标签数据预处理if not trained:self.ymin=0self.ymax=1return (y-self.ymin)/(self.ymax-self.ymin)
class LineSvc(Classification, LineSvmModel): #线性支持向量机分类器def __init__(self):self.tagVal=np.sign
程序中,
- 第3~28行定义的支持向量模型类SvmModel继承线性模型类LineModel(见博文《最优化方法Python计算:无约束优化应用——线性回归模型》)。类定义体中
- 第4~5行定义目标函数obj,返回值为 1 2 w ⊤ H w \frac{1}{2}\boldsymbol{w}^\top\boldsymbol{Hw} 21w⊤Hw,即优化问题的目标函数。
- 第6~24行重载训练函数fit。对比博文《最优化方法Python计算:无约束优化应用——线性回归模型》中定义的父类fit函数可见第7~16行的代码是保持一致的。第17行定义优化问题的不等式约束条件函数 g ( w ) = ( g 1 ( w ) g 2 ( w ) ⋮ g m ( w ) ) \boldsymbol{g}(\boldsymbol{w})=\begin{pmatrix}g_1(\boldsymbol{w})\\g_2(\boldsymbol{w})\\\vdots\\g_m(\boldsymbol{w})\end{pmatrix} g(w)= g1(w)g2(w)⋮gm(w) ,其中 g i ( w ) = y i ( x i ⊤ , 1 ) w − 1 g_i(\boldsymbol{w})=y_i(\boldsymbol{x}_i^\top,1)\boldsymbol{w}-1 gi(w)=yi(xi⊤,1)w−1, i = 1 , 2 , ⋯ , m i=1,2,\cdots,m i=1,2,⋯,m。第18行构造不等式约束条件 g ( w ) ≥ o \boldsymbol{g}(\boldsymbol{w})\geq\boldsymbol{o} g(w)≥o赋予cons,第19行调用minimize函数求解优化问题,返回值赋予res。第20行将res的x属性赋予w0。第21行调用父类的coef_inte函数(参见《最优化方法Python计算:无约束优化应用——线性回归模型》)计算决策面的系数coef_与截距intercept_。第22~23行调用Numpy的where函数,按条件
y i ( x i ⊤ , 1 ) w − 1 ≤ 1 1 0 6 , i = 1 , 2 , ⋯ , m y_i(\boldsymbol{x}_i^\top,1)\boldsymbol{w}-1\leq\frac{1}{10^6}, i=1, 2, \cdots, m yi(xi⊤,1)w−1≤1061,i=1,2,⋯,m
查找支持向量的下标集并赋予属性support_。
- 第25~29行重载标签数据归一化函数ynormalize。由于支持向量机模型中的标签数据不需要归一化,所以在训练时将self.ymin和self.ymax设置为0和1。第29行返回归一化后的标签数据。做了这样的调整,我们在进行预测操作时,式
y = y ⋅ ( max y − min y ) + min y y=y\cdot(\max y-\min y)+\min y y=y⋅(maxy−miny)+miny
仍保持 y y y的值不变,进而可保持LineModel的predict函数代码不变(参见《最优化方法Python计算:无约束优化应用——线性回归模型》)。 - 第30~32行定义的线性支持向量机分类器类LineSvc继承了Classification(见博文《最优化方法Python计算:无约束优化应用——线性回归分类器》)和LineSvmModel的属性与方法。在构造函数的第32行中将标签值函数tagVal设置为Numpy的sign函数,以便按式
y = sign ( ( x ⊤ , 1 ) w 0 ) y=\text{sign}((\boldsymbol{x}^\top,1)\boldsymbol{w}_0) y=sign((x⊤,1)w0)
计算分类预测值。
例1文件dataset.csv包含600个记录,每个记录由X、Y和Lable三个属性构成。其中X和Y描述样本点在平面中的笛卡尔坐标,Label表示样本分类值1或-1。前300个记录的标签值为1,后300个记录的标签为-1。
| X | Y | Lable |
|---|---|---|
| -0.0185 | 1.87 | 1 |
| 0.147 | 1.99 | 1 |
| -0.288 | 2.01 | 1 |
| ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ |
| 2.14 | -0.178 | -1 |
| 2.18 | 0.262 | -1 |
由X,Y作为坐标的样本在平面上的散点图如前图1所示。左上点簇的标签为1,右下点簇的标签为-1。这形成一个线性可分问题,下列代码用此数据集训练一个支持向量机模型。
import numpy as np #导入numpy
data = np.loadtxt('dataset.csv', delimiter = ',', #读取数据文件skiprows = 1) #去掉表头
X = np.array(data) #转换为数组
Y = X[:, 2].astype(int) #读取标签
X = np.delete(X, [2], axis = 1) #删除标签数据
m, _ = X.shape[0]
print('共有%d个样本数据。'%m)
a = np.arange(m) #下标集
np.random.seed(1006)
print('随机抽取%d个样本作为训练数据。'%(m // 10))
train = np.random.choice(a, m//10, replace=False) #随机取得一半作为训练集下标
test = np.setdiff1d(a, train) #测试集下标
svm = LineSvc() #支持向量机分类模型
svm.fit(X, Y) #训练模型
print('系数:%s'%svm.coef_) #决策平面系数
print('截距:%.4f'%svm.intercept_) #决策平面截距
print('支持向量下标:%s,对应的支持向量%s'%(svm.support_, X[train[svm.support_]]))
accuracy = svm.score(X, Y) * 100 #测试模型
print('分类正确率为%.2f' % (accuracy) + '%')
程序的第2~6行准备数据X和Y,读者利用代码内注释不难理解。第7~13将数据集随机地拆分成训练集X[train],Y[train]和测试集X[yest],Y[test]。第14行声明LineSvc类对象svm。第15行调用svm的fit函数用数据X[train]和Y[train]训练svm。第16~17行输出决策平面(直线)的系数coef_和截距intercept_。第18行输出X[train]中的支持向量下标svm.support_和对应的向量。第19行调用svm的score函数用X和Y测试svm。第20行输出测试正确率。运行程序,输出
共有600个样本数据。
随机抽取60个样本作为训练数据。
训练中...,稍候
4次迭代后完成训练。
系数:[-0.6 0.7]
截距:-0.0
支持向量下标:[26 39],对应的支持向量[[0.2 1.7][1.8 0.2]]
分类正确率为100.0%
意为经过4次迭代训练所得支持向量机模型中的决策平面(直线) π \pi π: − 0.6 x 1 + 1.7 x 2 = 0 -0.6x_1+1.7x_2=0 −0.6x1+1.7x2=0。两个支持向量: ( x 1 , x 2 ) = ( 0.2 , 1.7 ) (x_1,x_2)=(0.2,1.7) (x1,x2)=(0.2,1.7)和 ( x 1 , x 2 ) = ( 1.8 , 0.2 ) (x_1,x_2)=(1.8, 0.2) (x1,x2)=(1.8,0.2)。将它们代入决策平面可算得分别对应1和-1。对测试数据的测试正确率为100%,可见这是一个线性可分问题。
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
相关文章:

最优化方法Python计算:有约束优化应用——线性可分问题支持向量机
设问题的数据样本点 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi,yi), x i ∈ R n \boldsymbol{x}_i\in\text{R}^n xi∈Rn, y i 1 y_i\pm1 yi1, i 1 , 2 , ⋯ , m i1,2,\cdots,m i1,2,⋯,m。由于标签数据 y i ∈ { − 1 , 1 } y_i\…...

Linux 离线安装 Docker 和 Docker Compose 最新版 的完整指南
一、准备工作 1. 下载安装包(需在有网络的机器操作): Docker 引擎:从官方仓库下载最新二进制包 wget https://download.docker.com/linux/static/stable/x86_64/docker-24.0.6.tgzDocker Compose:下载最新二进制…...

SpringBoot学习(上) , SpringBoot项目的创建(IDEA2024版本)
目录 1. SpringBoot介绍 SpringBoot特点 2. SpringBoot入门 2.1 创建SpringBoot项目 Spring Initialize 第一步: 选择创建项目 第二步: 选择起步依赖 第三步: 查看启动类 2.2 springboot父项目 2.3 测试案例 2.3.1 数据库 2.3.2 生成代码 1. SpringBoot介绍 Spring B…...
——栈的应用—数制转换)
数据结构(四)——栈的应用—数制转换
利用栈进行数制转换: 十进制转换八进制:先将十进制数除以八得到余数,余数入栈,然后将得到的商继续除以八,直到商为零 #include <stdio.h> #include <stdlib.h>#define MAXSIZE 100//数制转换//定义链表节…...

多视角系统,视角之间的切换,输入操作。无人机Pawn视角的实现
一.创建自己的PlayerController。它相当于是灵魂,穿梭在不同Pawn之间。也即是切换视角。不同输入的响应也写在这里。这样即使,都有鼠标操作,也能区分。避免了代码的重复耦合。也可以叫做视角系统。 class LZJGAMEMODE_API ALZJPlayerControl…...

【Redis 进阶】哨兵模式
思维导图: 一、哨兵模式概述 (一)传统主从复制模式的局限性 在传统的Redis主从复制架构中,若主节点发生故障,运维人员需手动执行故障转移操作,将一个从节点提升为新主节点,并逐一通知所有客户…...
)
掌控随心 - 服务网格的流量管理艺术 (Istio 实例)
掌控随心 - 服务网格的流量管理艺术 (Istio 实例) 想象一下,没有服务网格的时候,我们要实现像“将 1% 的用户流量导入到新版本应用”、“根据用户设备类型访问不同后端”、“模拟下游服务故障”这类高级流量策略,通常需要在代码、负载均衡器、API 网关等多个地方进行复杂且分…...

在服务器排查java某个线程导致CPU飙高教程
🧩 第一步:确定是哪个线程占用 CPU 高 1.1 使用 top 或 htop 命令查看高 CPU 的 Java 进程 top -Hp <Java进程PID>-H 表示显示线程级别;-p 后面跟 Java 主进程的 PID;你会看到各个线程的 CPU 使用情况,找出使用…...

电子商城后台管理平台-Flask Vue项目开发
电子商城后台管理系统 电子商城后台管理平台-Flask 项目开发 文章目录 前言网课内容数据库参数用户模块/user/前端LESS 的语法使用LESS 的特点 ui登录页面主页页面头部左边aside 菜单main主体后端main页面设置用户-角色-权限商品分类商品信息图片保存到项目里面订单数据展示 网…...

Lettuce 节点刷新、连接优化与 Spring 升级适配全解析:从环境约束到生产验证
引言 在分布式系统中,Redis 作为高性能缓存中间件被广泛使用。随着 Spring 生态的迭代(尤其是 Spring Boot 2.0 的普及),Lettuce 逐渐取代 Jedis 成为 Redis 客户端的 “默认选择”。但开发者常面临三个核心问题:Let…...
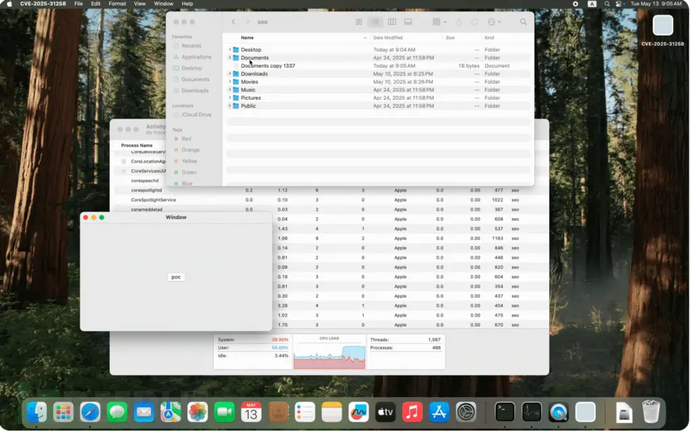
CVE-2025-31258 macOS远程视图服务沙箱逃逸漏洞PoC已公开
苹果公司近日针对macOS系统中新披露的CVE-2025-31258漏洞发布补丁,该漏洞可能允许恶意应用程序突破沙箱限制,获取未授权的系统资源访问权限。在安全研究员Seo Hyun-gyu公开概念验证(PoC)利用代码后,该漏洞已在macOS Se…...

UDP协议详细讲解及C++代码实例
目录 一、UDP协议概述二、UDP通信流程1)数据传输2)无连接 三、关键点解析1) 套接字创建2)无连接特性3)数据传输 四、总结 UDP协议详细讲解及C代码实例 一、UDP协议概述 UDP(User Datagram Protocol,用户数据报协议&a…...

武汉大学无人机视角下的多目标指代理解新基准!RefDrone:无人机场景指代表达理解数据集
作者:Zhichao Sun, Yepeng Liu, Huachao Zhu, Yuliang Gu, Yuda Zou, Zelong Liu, Gui-Song Xia, Bo Du, Yongchao Xu 单位:武汉大学计算机学院 论文标题:RefDrone: A Challenging Benchmark for Drone Scene Referring Expression Compreh…...

【递归、搜索和回溯】二叉树中的深搜
个人主页 : zxctscl 专栏 【C】、 【C语言】、 【Linux】、 【数据结构】、 【算法】 如有转载请先通知 文章目录 前言1 2331. 计算布尔二叉树的值1.1 分析1.2 代码 2 129. 求根节点到叶节点数字之和2.1 分析2.2 代码 3 814. 二叉树剪枝3.1 分析3.2 代码 4 98. 验证…...

Algolia - Docsearch的申请配置安装【以踩坑解决版】
👨🎓博主简介 🏅CSDN博客专家 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入!…...

Linux513 rsync本地传输 跨设备传输 一
ping节点bPing通 仅主机模式不需要设置网关节点a也可以Ping通节点b 同步成功 下载文件夹成功 今日源码 节点a 节点b...

leetcode 383. Ransom Note
题目描述 代码 class Solution { public:bool canConstruct(string ransomNote, string magazine) {vector<int> table(26,0);for(char ch : magazine){table[ch-a];}for(char ch : ransomNote){table[ch-a]--;if(table[ch-a] < 0)return false;}return true;} };...

Skyvern:用 AI+视觉驱动浏览器自动化
Skyvern:用 AI视觉驱动浏览器自动化 一、前言二、项目概览2.1 Skyvern 项目简介2.2 代码结构与模块划分 三、环境搭建与快速上手3.1 环境准备3.1.1 系统与依赖3.1.2 克隆项目3.1.3 安装 Python 依赖3.1.4 配置环境变量3.1.5 启动服务 3.2 验证安装 四、核心功能与实…...

数据库原理期末考试速成--最后附带两套题
引言 为什么从3开始呢,毕竟是速成吗,总要放弃一些东西 前两章1.概论 2.关系数据库:这里面都是一些运算符什么的,我感觉都学这个:笛卡尔积之列的都会算 这两章比较重要的我就放在这里了 选择、投影、连接、除、并、交、差,其中选择、投影、并、差、笛卡尔积是5种基本关…...

《探索React Native社交应用中WebRTC实现低延迟音视频通话的奥秘》
WebRTC,全称为Web Real-Time Communication,是一项开创性的开源技术,为Web和移动应用开启了实时通信的大门。它打破了传统通信的束缚,使得应用之间无需依赖繁琐的中间服务器,就能实现直接的点对点通信,这是…...

关于vue 本地代理
接口调用:其中我们可以约定一个拦截的标识, 用来给本地 http://localhost/ 进行代理要请求的测试地址https:abc.com 例子: axios.post(/OwnRateReport/-------------------------------------------------------00001)devServer: {proxy: {/…...

#跟着若城学鸿蒙#HarmonyOS NEXT学习之Blank组件详解
一、组件介绍 Blank(空白)组件是HarmonyOS NEXT中一个简单但非常实用的UI组件,它主要用于在布局中创建空白区域,帮助开发者更灵活地控制界面元素之间的间距和布局结构。虽然Blank组件本身不显示任何内容,但它在界面设…...
通过自定义 MAVLink 消息与 QGroundControl (QGC) 通信)
PX4开始之旅(二)通过自定义 MAVLink 消息与 QGroundControl (QGC) 通信
核心知识点:通过自定义 MAVLink 消息与 QGroundControl (QGC) 通信 1. 通俗易懂的解释 想象一下,MAVLink 就像是无人机(飞控)和地面站(QGroundControl)之间约定好的一种“语言”。这种语言有很多标准的“…...

数据结构基础--蓝桥杯备考
1.优缺点总述 STL中各容器对比图 各类线性数据结构优缺点 1.数组 1.优点 1.简单,容易理解 2.访问快捷,只需要用下标就可以 3.有某些应用场景直接对应,例如二维数组对应平面 2.缺点 删除和插入数据非常耗时 2.链表 1.优点 插入和删…...

2.4GHz无线通信芯片选型指南:集成SOC与低功耗方案解析
今天给大家分享几款2.4GHz无线通信芯片方案: 一、集成SOC芯片方案 XL2407P(芯岭技术) 集成射频收发机和微控制器(如九齐NY8A054E) 支持一对多组网和自动重传 发射功率8dBm,接收灵敏度-96.5dBm(…...

安卓刷机模式详解:Fastboot、Fastbootd、9008与MTK深刷
安卓刷机模式详解:Fastboot、Fastbootd、9008与MTK深刷 一、刷机模式对比 1. Fastboot模式 简介:传统安卓底层刷机模式,通过USB连接电脑操作优点:支持大多数安卓设备,操作相对简单缺点:需要设备进入特定…...
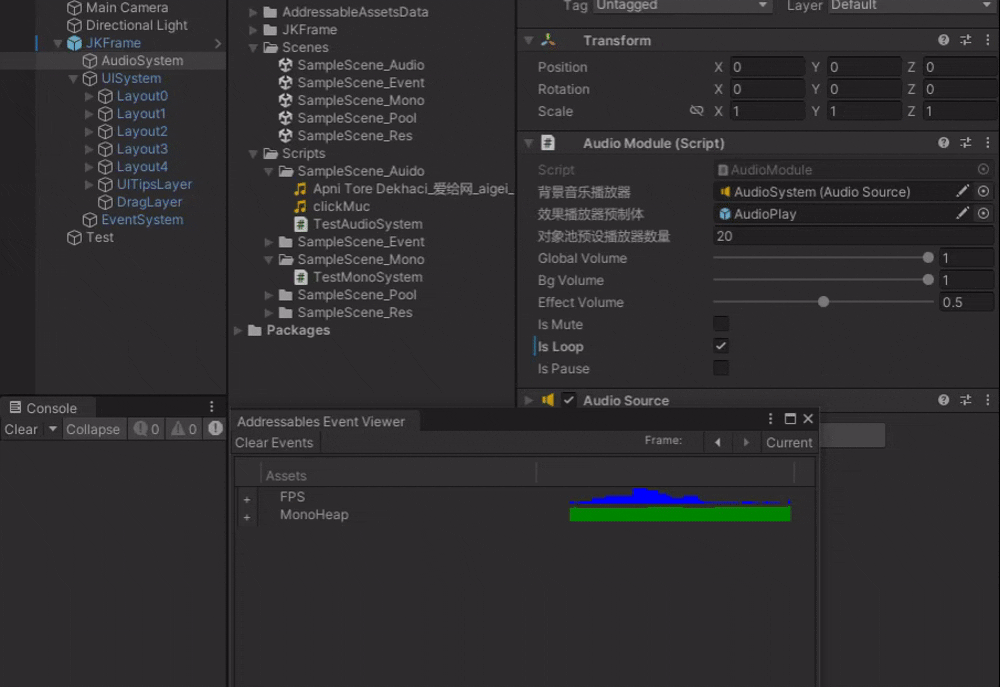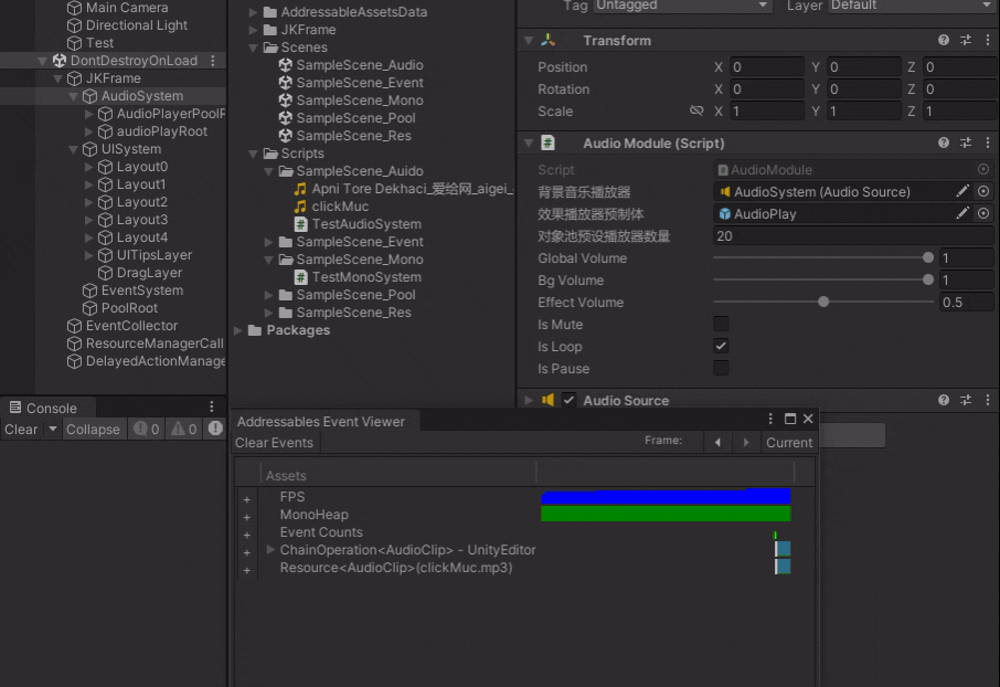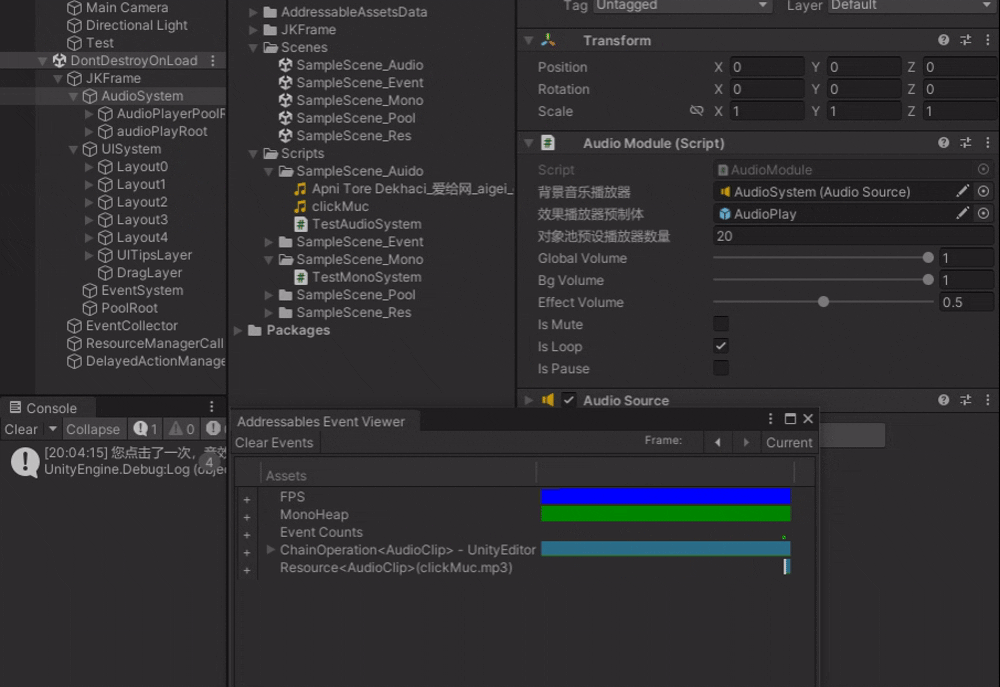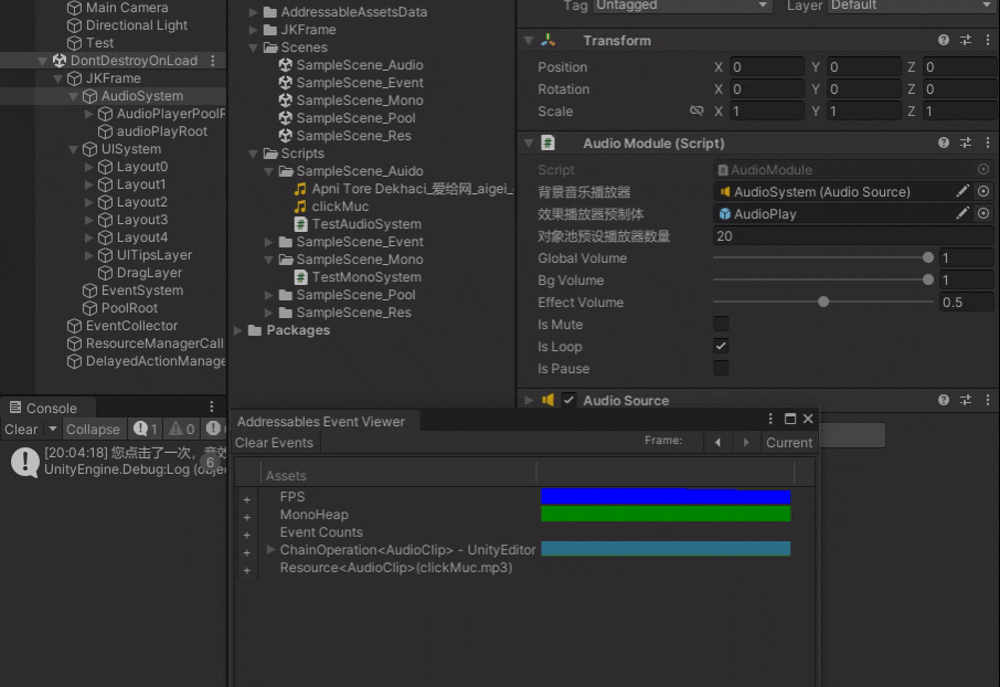
Unity_JK框架【5】音效系统实现
在游戏开发中,音频是不可或缺的一部分,它能够极大地增强游戏的沉浸感和趣味性。今天,我们就用JK框架 探讨一下如何在Unity中实现一个强大的音频系统,并且通过实际的测试脚本来验证其功能👏。 一、音频模块类࿱…...

鸿蒙 从打开一个新窗口到Stage模型的UIAbility组件
打开一个新的窗口 我们首先来实现如何在一个应用中打开一个新窗口,使用的模型是 Stage 模型 在项目文件里,新建一个 newWindow.ets 新文件 src/main/ets/pages/newWindow.ets newWindow.ets文件里面随便写点什么都行,这里是第一步创建的文件…...

MySQL数据库——视图
目录 一、视图是什么? 二、特点 三、创建视图 四.查询视图 五.更新视图 六.视图的作用 总结 一、视图是什么? 视图是从一个或多个表中导出的虚拟表,它本身不存储数据,而是基于 SQL 查询的结果集。 二、特点 1.虚拟性࿱…...
)
redis数据结构-09 (ZADD、ZRANGE、ZRANK)
Redis 排序集简介:ZADD、ZRANGE、ZRANK Redis 有序集合是一种功能强大的数据结构,兼具集合和哈希的特性。它维护一组唯一元素,类似于集合;但每个元素都与一个分数相关联,类似于哈希。分数用于对有序集合中的元素进行排…...
